【深度学习】从VAE到GAN漫谈

正文

从AE说起

AE是一个特征提取模型，通过编解码的形式重构输入，完成低维特征表示工作

推导

存在一个输入$x$，构造AE编码器$p_\theta(x)$，得到离散低维特征$z$；
通过AE解码器$q_\phi(z)$，重构回$\hat{x}$；
通过正则项$\Vert x-\hat{x} \Vert_2$构造损失函数实现。

\[\begin{aligned} z &= p_\theta(x) \\ \hat{x} &= q_\phi(z) \\ \mathcal{L} &= \frac{1}{2}\Vert x-\hat{x} \Vert_2 \end{aligned} \]

缺点

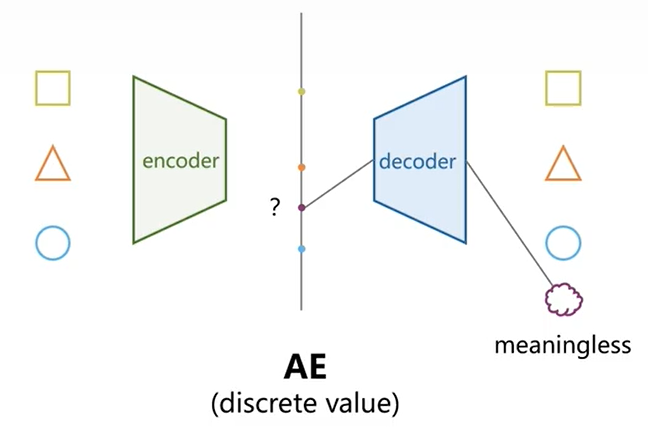
AE的$x->z->\hat{x}$是一一映射确定的关系，这就意味着作为一个生成模型他是不够格的，想象一下我有一批样本$\{x_1,x_2,\dots,x_n\}$，对其进行AE训练可得对应的低维特征$\{z_1,z_2,\dots,z_n\}$，当作为生成模型时我只能从有限离散的低维特征簇中随机选择现有的特征$z_i$输入我的解码器$\hat{x_i}=q_\phi(z_i)$，得到原先样本中已有的一张图、一段信号等。

而当我们想从，举例$z_1、z_2$之间取一个$z_{1.5}$（不太严谨的说法，主要想表面取一个低维特征簇之外的特征）时，由于没有受过训练，得到的一定是一个很诡异的东西。

VAE的诞生

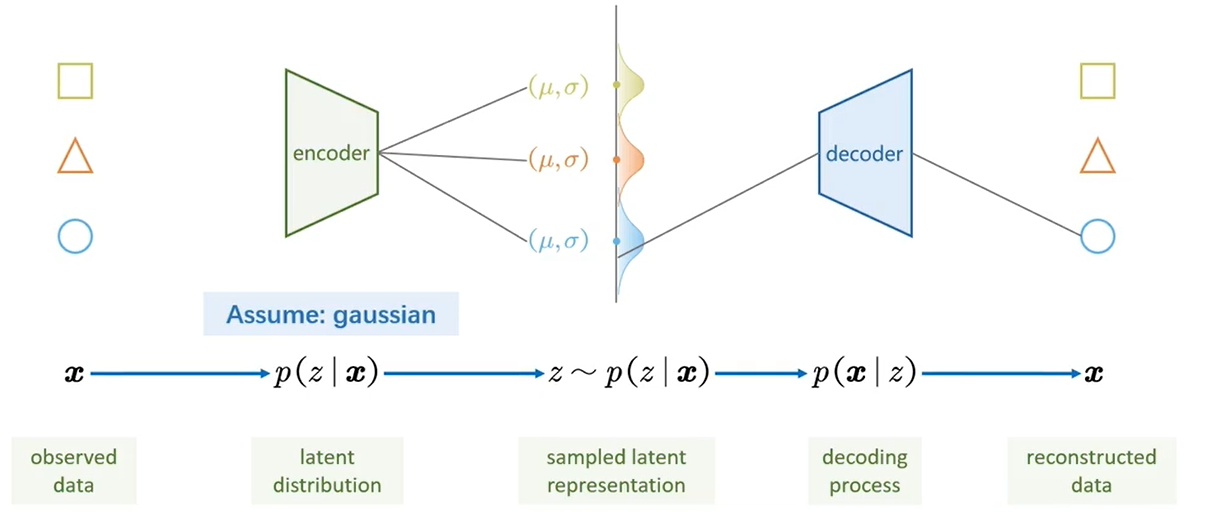
VAE与AE最大的不同在于，提出潜变量z的概念，将潜变量z由离散的分布->连续的分布，这使得生成模型得以实现，由于z可以从连续分布中任意采样，大大的增大了作为生成模型的性能。

1. 加点噪声吧

原先在AE中，所有的$z_i$可以理解为由单独一个编码器$\mu(x)$得到的均值$\mu$，可知这个$\mu$是离散且服从狄拉克分布的。因此在$\mu$周围采样，甚至距离$\mu_i$特别接近也只能生成近似于$x_i$的图像。

![[AE特征分布]]

在AE中看起来是没办法提取一个$z_{n+1}$去生成了，那如果加点噪声呢？额外添加一个编码器$\sigma(x)$作为我的噪声，让我的$z_i$增加不确定性，每次都是从一个$p(z_i)$分布中采样得到的，那么我在这些分布的交叉处就可以获得保留各自输入样本特征的图像啦！

![[CVAE特征分布]]

$!NOTE$
实际上，这是CVAE的特征分布示意图，每种类图像（以MNIST为例）的$z_i$潜变量分布都对应有一个$\mu_Y$均值、1为方差的高斯分布

上述描述与真实的VAE还存在一些不同：

VAE的$z$分布我们希望它光滑且连续，这样我们才能从中任意采样确保能得到有意义的图像，所以在后文提到使用正则化项KL散度限制所有的$z$分布->标准高斯分布；
z的采样具有随机性，因此是不可梯度回传的，我们使用一种重参数化技巧，把从$N(\mu,\sigma)$随机采样转变为随机生成一个$\epsilon \sim N(0,1)$噪音，$z=\mu + \epsilon * \sigma$；

把$\{z_1,z_2,\dots,z_n\}$强制约束到一个分布$q(z)$（例如正态分布），那么我就可以通过$z\sim q(z)$的方式从这个光滑连续的分布中采样并生成图形了。

$!question\] 为什么AE中也可以采样，但是VAE采样可以生成有意义图形？ 1. AE的\$z\$与\$x\$之间是一一对应的，没有经过训练的\$z_i\$没有对应的物理含义； 2. VAE中每次训练都强制性把\$q(z\|x)\$后验分布约束为一个\$N(0,I)\$分布，这样每次训练都经历这一步，后续我从\$N(0,I)\$分布中就算采样得到的\$Z\$并没有在训练中出现过，也能实现保留部分特征的效果； 3. 从数学的角度而言，每次训练过程中是从如下分布取到的，而正则化项迫使\$\\mu(x)-\>0\$、\$\\sigma(x)-\>1\$形成一个标准的正态分布；然而重构损失项也会为了尽可能高的精度去抹平噪声项\$\\sigma(x)\$，并且使得\$\\mu(x)\$还原回原先AE中离散的位置。这种天然的**对抗** 其实也含有GAN中对抗的哲学，并且最终形态也可知\$q(z\|x)\$一定不是一个标准正态分布，而是保留了其趋向于表征其特征的\$\\mu(x)\$的趋势，因此这也可以解释为什么VAE的潜变量空间会呈现一定的分块或者说聚类性。 \\\[z \\sim q(z\|x) = N(\\mu(x);\\sigma(x)I) \\$

现在还存在一个问题，就是$z$和$x$不匹配，如果$[\mu, \sigma] \sim [\mu(X),\sigma(X)]$，那么我采样出来的$z$到底是对应了哪个$x$呢？我解码后的$\hat{x}$又该和哪个$x$去做对比呢？所以我们提出$z \sim q(z|x)$：

$z_i \sim q(z|x_i)$
$\hat{x_i}=decoder(z_i)$
$\mathcal{L}=D(x_i, \hat{x_i})$

并且当$q(z|x) \sim N(0,I)$后，$q(z)$也自然的服从标准正态分布

\[q(z)=\int q(x,z)dx=\int q(z|x)q(x)dx=q(z|x)\int q(x)dx=q(z|x) \sim N(0,1) \]

太好了，这下我们有救了。

2. 无中生有

现有一批样本$\{x_1,x_2,\dots,x_n\}$，根据贝叶斯学派的观点，一定是服从一个证据分布$\tilde{p}(x)$

通常我们可以假设存在一个潜变量$z$，这个$z$是物理空间观测到的$\{x_1,x_2,\dots,x_n\}$样本的潜在表达，并且根据第一节的内容我们知道，这个$z$最好是从$p(z|x)$分布中采样的。

那么只要我们知道$p(z|x)$后，可以得到一一对应的$x$与$z$的关系，并且可以开展后续的$z$采样和解码工作，然而如下式，对$p(z|x)$的直接求解是不现实的。

\[\begin{aligned} p(z|x) = \frac{p(z,x)}{\tilde{p}(x)}= \frac{p(x|z)p(z)}{\int_z p(x,z)dz}= \frac{p(x|z)p(z)}{\int_z p(x|z)p(z)dz} \end{aligned} \]

$!NOTE$
主要是在分母中涉及到对z求边缘积分，我的理解是z是没有边际的很难求解

那么转换一下思路，不能求解$p(z|x)$，我还不能拟合一个和$p(z|x)$近似的分布吗？答案是当然可以，不妨假设一个分布$q(z|x)$。让这二者逼近的同时，保留$q(z|x)$的高斯分布特性，那么届时也可完成$z$的采样、解码等后续操作。

这里参考苏剑林苏神的方法，让$q(x,z)$与$p(x,z)$逼近，由下式可知，具有更高的证据下界，是一种更强限制性、更严谨的做法。

\[\begin{aligned} KL(p(x,z)||q(x,z))&=\iint p(x,z)ln\frac{p(x,z)}{q(x,z)}dxdz \\ &=\iint p(x,z)ln\frac{\tilde{p}(x)p(z|x)}{q(x)q(z|x)}dxdz \\ &=\iint \tilde{p}(x)p(z|x)(ln\frac{\tilde{p}(x)}{q(x)}+ln\frac{p(z|x)}{q(z|x)})dxdz \\ &=\iint \tilde{p}(x)p(z|x)ln\frac{\tilde{p}(x)}{q(x)}dxdz+\iint \tilde{p}(x)p(z|x)ln\frac{p(z|x)}{q(z|x)})dxdz \\ &=\int_x \tilde{p}(x)ln\frac{\tilde{p}(x)}{q(x)}[\int_z p(z|x)dz]dx+\int_x \tilde{p}(x)[\int_z p(z|x)ln\frac{p(z|x)}{q(z|x)}dz]dx \\ &=\int_x \tilde{p}(x)ln\frac{\tilde{p}(x)}{q(x)}dx+\int_x \tilde{p}(x) KL(p(z|x)||q(z|x))dx \\ &=KL(\tilde{p}(x)||q(x)) + \int_x \tilde{p}(x) KL(p(z|x)||q(z|x))dx \\ \end{aligned} \]

3. 神经逼近

通过散度值，我们可以定义一个优化目标，即$KL(p(x,z)||q(x,z))$越接近于0越好，其中$q(x,z)$是我们假设存在且可控的一个分布，$q(x,z)=q(z|x)q(x)=q(x|z)q(z)$。

在后续公式推导前，我还是要明确所有符号的意义：

$q(x,z)$：假设存在的一个联合概率密度函数；
$q(x|z)$：假设存在的似然分布；
$q(z|x)$：假设存在的后验条件概率分布；
$q(z)$：假设存在的先验分布；
反之，关于$p$符合的都是证据分布$\tilde{p}(x)$潜变量空间中真实存在的。

开始吧。

\[\begin{aligned} KL(p(x,z)||q(x,z))&=\iint p(x,z)ln\frac{p(x,z)}{q(x,z)}dxdz \\ &=\int_x \tilde{p}(x)[\int_zp(z|x)ln\frac{p(x,z)}{q(x,z)}dz]dx \\ &=\mathbb{E}{x \sim \tilde{p}(x)}[\int_zp(z|x)ln\frac{\tilde{p}(x)p(z|x))}{q(x,z)}dz] \\ &=\mathbb{E}{x \sim \tilde{p}(x)}[\int_zp(z|x)ln \tilde{p}(x)dz + \int_zp(z|x)ln\frac{p(z|x)}{q(x,z)})] \end{aligned} \\ \]

其中

\[\mathbb{E}{x \sim \tilde{p}(x)}[\int_zp(z|x)ln \tilde{p}(x)dz]=\mathbb{E}{x \sim \tilde{p}(x)}[ln \tilde{p}(x)] \]

是真实存在的证据分布$\tilde{p}(x)$的信息熵，记作常数$C$

因此$KL(p(x,z)||q(x,z))=C+\mathbb{E}_{x \sim \tilde{p}(x)}[\int_zp(z|x)ln\frac{p(z|x)}{q(x,z)})dz]$，因此最小化$KL(p(x,z)||q(x,z))$相当于最小化后面那项

\[\mathcal{L}=KL(p(x,z)||q(x,z))-C=\int_zp(z|x)ln\frac{p(z|x)}{q(x,z)})dz \]

并且我们可以说$\mathcal{L}$存在下界$-C$。

接着来

\[\begin{aligned} \mathcal{L}&=\mathbb{E}{x \sim \tilde{p}(x)}[\int_zp(z|x)ln\frac{p(z|x)}{q(x,z)})dz] \\ &=\mathbb{E}{x \sim \tilde{p}(x)}[\int_zp(z|x)ln\frac{p(z|x)}{q(x|z)q(z))})dz] \\ &=\mathbb{E}{x \sim \tilde{p}(x)}[\int_zp(z|x)ln\frac{p(z|x)}{q(z)}dz-\int_zp(z|x)lnq(x|z)dz] \\ &=\mathbb{E}{x \sim \tilde{p}(x)}[KL(p(z|x)||q(z))-\mathbb{E}_{z \sim p(z|x)}[lnq(x|z)]] \end{aligned} \]

得到原作者论文中的损失函数式子。

4. 直观的物理意义

首先要牢记一点，最小化$\mathcal{L}$。

第一项：$-\mathbb{E}_{z \sim p(z|x)}[lnq(x|z)]$

KL项已经存在下界0了，所以应该是最大化$\mathbb{E}_{z \sim p(z|x)}[lnq(x|z)]$，怎么理解呢？

官方名字应该叫做，当$z$采样于$p(z|x)$分布时，最大对数似然函数的期望

可以理解为：

$z$目前已经完成从$p(z|x)$分布中采样得到了；
这个条件概率分布$q(x|z)$理解为固定$z$，对$q(x)$分布进行积分；
$\mathbb{E}{z \sim p(z|x)}[lnq(x|z)] \approx \frac{1}{k}\sum{i=1}^k{lnq(x_i|z)}$，以离散的形式看会更清晰，固定$z$后生成$x_i$的期望；

这项越大，表示重构的$\hat{x}$越接近于$x$。

第二项：$KL(p(z|x)||q(z))$

这个就不用多说了，KL代表两个分布之间的近似程度，一般我们会假设$q(z) \sim N(0,I)$，所以我们是对$p(z|x)$这一项进行了约束，让其接近于标准正态分布。这样有两个好处：

方便后续作为生成模型采样；
强制性的添加噪声，提高encoder的噪声鲁棒性，以及防止退化为一个自编码器模型；

GAN暴力解决

0. 前言

关于上一节中VAE的一些概念，再进行补充：

\[\begin{aligned} p(x)&=\int_z p(x,z)dz=\int_zp(x|z)p(z)dz \\ p(z) &= \int_xp(x,z)dx=\int_xp(z|x)\tilde{p}(x)dx \end{aligned} \]

上述两个公式分别还原了在VAE中编码器与解码器的工作。

如前面节所述，后验分布$p_\theta(z|x)$较难计算得到，所以需要用一个神经网络$q_\phi(z|x)$进行拟合；

之所以不使用一个$q_\phi(x|z)$对似然分布$p_\theta(x|z)$进行拟合主要是由于：

![[002 VAE详细文档#一些补充---对变分推断的一些思考]]

1. 背景

一道面试题：

现有生成服从均匀分布的一个随机数生成程序，那如何据此去做一个生成符合正态分布的随机数 据呢？即，如何从均匀分布X_{U[0,1]转化为正态分布Y}N(0,1)？

\[Y=f(X) \]

是否可以寻找一个映射关系，让$X$与$Y$实现一一对应，通过这个映射使得均匀分布映射为正态分布？

那么这个映射关系一定使得$X \sim U[0,1]$和$Y \sim N(0,1)$都符合$[x,x+dx]$区间的概率与$[y,y+dy]$区间的概率相同，即：

\[\int_0^x \rho(t)dt=\int_{-\infty}^y \phi(t)dt=\int_{-\infty}^y\frac{1}{\sqrt{2\pi}}exp(-\frac{t^2}{2})dt=\Phi(y) \]

$!NOTE$
为什么说[x, x+dx]区间的概率和[y, y+dy]区间的概率相同？

上面的区间概率实际上只是连续概率密度函数中，计算一个点对应的概率值 ，针对$X$的样本记作$\rho(x)$，针对$Y$的样本记作$\phi(y)$；

倒推来说，我们希望最后服从均匀分布的随机数程序生成一个数，例如0.7，我们希望它能经过映射关系f后转化到对应的正态分布数据0.5244（实际上我们希望一个服从正态分布的随机数程序可以直接生成这个数），所以换言之，我们希望均匀分布随机数程序生成0.7的概率和正态分布随机数程序生成0.5244的概率是相同的 ，是一种一一对应的映射关系；

其中$\Phi(y)$是指标准正态分布的累计分布函数（Cumulative Distribution Function)

因此，$y$其实可以由CDF的逆函数表达：

\[y=\Phi^{-1}(\int_0^x\rho(t)dt) \]

但是但是，CDF是没有一个显式的函数表达式的！因此，求逆显然也是不可行的。

举这个例子只是想说，从均匀分布->标准正态分布的过程已是如此艰难，更不用说一些我们无法说出分布的离散例子了。

2. 神经推导

那咋办呢？

简单，上神经网络呗，特别要记住遇到$f(*)$就要想到神经网络，有点类似于当年米开朗基罗那种

给我一个支点，我就可以翘起一个地球

的豪迈，基本上一个显式或隐式的函数都可以通过神经网络拟合得到。

既然具备了利器，那我们收敛回现实，讨论一下比正态分布更复杂的分布，并且这类分布通常是由$Z=\{z_1,z_2,\dots,z_n\}$这些样本来描述的（比如我们只能给出一批图片的样本，而无法告诉我们的网络这批图片遵从什么分布，又或者说我知道图片遵从什么分布了还需要你生成模型干啥？），我们的GAN所做的事情就是把噪声（标准正态分布）映射到这堆数据背后的分布中去。

来吧，拟合

\[Y=G(X;\theta) \]

特别用了$G$来表示Generative，生成模型。通过把噪声$X$输入到这个$G$中，得到一个希望逼近于真实图片分布的一个$Y$分布。

$!NOTE$
重点注意这里，X和Y都大写表示分布，如上文所述是分布到分布的映射。

通常来说，两个分布的接近程度我们可以使用

\[\begin{aligned} KL(p_1(x)||p_2(x))&=\int p_1(x)log\frac{p_1(x)}{p_2(x)}dx\\ JS(p_1(x),p_2(x))&=\frac{1}{2}KL(p_1(x)||p_2(x))+\frac{1}{2}KL(p_2(x)||p_1(x)) \end{aligned} \]

上述二者的区别在于KL距离是不对称的，即$KL(p_1(x)||p_2(x))$和$KL(p_2(x)||p_1(x))$是不相等的 。但是JS距离是对称的。

anyway，现在没有概率分布，就勉强用频率来代替一下，先看看能不能计算距离再说。

\[\begin{aligned} p_z(I_i) &=\frac{1}{N} \sum_{j=1}^N \#(z_j \in I_i) \\ p_y(I_i) &=\frac{1}{M} \sum_{j=1}^M \#(y_j \in I_i) \end{aligned} \]

$!NOTE\] Example 我现在有\$\\{1.2, 1.5, 2.3, 3.1, 3.6, 4.0, 4.2, 5.7, 6.1, 6.8\\}\$这些数据，我需要评估这些数据背后的分布，使用上述公式整体步骤如下： 1. 划分区间，\$I_1=\[1,3)、I_2=\[3,5)、I_3=\[5,7)\$； 2. 统计落在每个区间内的个数，\$C(I_1)=3、C(I_2)=4、C(I_3)=3\$； 3. 计算\$p(I_1)=\\frac{3}{10}=0.3、p(I_2)=\\frac{4}{10}=0.4、p(I_3)=\\frac{3}{10}=0.3\$；$

注意到$y$是由$G(X;\theta)$生成的，所以应该使用$p_y(I_i;\theta)$表示，那么我们可以通过构建：

\[\begin{aligned} \mathcal{L}&=JS(p_y(I_i;\theta),p_z(I_i)) \\ \theta &= \mathop{\arg \min} \limits_{\theta}\mathcal{L} \end{aligned} \]

得到最终的生成器网络参数$\theta$。

但是但是但是，对于多元变量的概率分布 而言。计算复杂度是巨大的。假设一张MNIST的手写数据集照，它的维度是28*28=784的，用上述方法统计它的频率，那划分的区间就是：

\[\mathop{\{0,1\},\{0,1\},\dots, \{0,1\}}\limits_{782} \]

$2^{784} \approx 10^{236}$量级！

还是换个方法吧...

3. 神经距离

说白了，距离不就是

\[\mathcal{L}=f(\{y_i\}{i=1}^M, \{z_i\}{i=1}^N) \]

只不过也是一个映射关系，也是一个函数罢了。

对了，上神经网络吧，我让神经网络帮我打分 ，帮我看他们的分布差距！

\[\mathcal{L}=f(\{y_i\}{i=1}^M, \{z_i\}{i=1}^N; \Theta) \]

$!NOTE$
GAN的高明之处就在于，连距离都是暴力求解 的，相比VAE使用KL散度去衡量$q_\phi(z|x)$和$p_\theta(z|x)$之间的距离，VAE简直太文艺了。尤其注意一点，我这里也不使用 $p_y(I_i)$频率去估计给出样本的分布了，把这步变换直接放入神经网络自己算去吧。

但是这种算法，我应该保障：输入顺序的改变（shuffle）不改变数据的分布，所以需要进行一步无序化的操作，这类操作在计算离散的样本之间的分布距离 （尤其是在聚类任务中）经常用到：

\[\mathcal{L}=\frac{1}{M!}\sum^{对所有y_1,\dots,y_M可能的排列求和}{j=1}D(\{y_i\}{i=1}^M, \{z_i\}_{i=1}^N; \Theta) \]

若$D(y_i,\Theta)$表示$y_i$到聚类中心$\Theta$的欧氏距离，则上述$\mathcal{L}$表示簇内平均距离；

若$D(y_i,\Theta)$表示$y_i$与理论分布$q_{\Theta}(y)$的负对数似然，则上述$\mathcal{L}$表示近似KL散度；

上述是大数定理 的体现，宗旨是数量足够多的时候，个体差异的均值可以表征整体差异状态。

\[\begin{aligned} D(y_i,\Theta)&=-log q_{\Theta}(y_i)，表示与理论分布的负对数似然\\ \{y_i\}{i=1}^M &\sim P{emp}，表示离散样本假设服从一个经验分布，Q_{\Theta}表示理论分布\\ KL(P_{emp}||Q_{\Theta})&=\int P_{emp}log\frac{P_{emp}}{Q_{\Theta}}=\int P_{emp}logP_{emp}-\int P_{emp}logQ_{\Theta}\\ &=H(P_{emp})-\mathbb{E}{y \sim P{emp}}[logq_{\Theta}(y)] \\ &\approx -\sum_{i=1}^M\frac{1}{M}log\frac{1}{M}-\frac{1}{M}\sum_{i=1}^Mlogq_{\Theta}(y_i)\\ &=logM+\frac{1}{M}\sum_{i=1}^MD(y_i,\Theta)\\ &\approx \frac{1}{M}\sum D(y_i,\Theta),M\rightarrow\infty \end{aligned} \]

$!NOTE\] 感性认知一、\$-logq_{\\Theta}(y_i)\$表示样本在理论分布\$Q\$下**的`不匹配程度`或者说`不符合预期程度`**，具体来说： 1. 如果\$q_{\\Theta}(y_i)\$越大，表示\$y_i\$满足这个分布的可能性越高，但是\$-logq_{\\Theta}(y_i)\$会越小，表示`符合预期`，表示`意外程度低`； 2. 反之，如果\$q_{\\Theta}(y_i)\$越小，表示\$y_i\$满足这个分布的可能性越低，但是\$-logq_{\\Theta}(y_i)\$会越大，表示`不符合预期`，表示\`意外程度高；二、交叉熵\$H(P,Q)=-\\int P_{emp}logQ_{\\Theta}=-\\mathbb{E}_{y \\sim P_{emp}}\[logq_{\\Theta}(y)\]\\approx\\frac{1}{M}\\sum_{i=1}\^Mlog-q_{\\Theta}(y_i)\$，其实**表征了所有样本的负对数似然的平均值** ，表示`用分布Q编码真实分布P的样本所需要的平均信息量`；三、KL散度\$KL(P\|\|Q)=H(P,Q)-H(P)\$，本质上是，去除`P`本身的不确定性（熵的定义）后，Q对于P的额外信息损失，是**衡量分布差异的度量** （因此也可以理解\$KL(P\|\|Q)\$和\$KL(Q\|\|P)\$不一样啦\~）$

证明到此结束，我想说的是，在数据量够多的情况下，直接使用

\[\mathcal{L}=\frac{1}{M}\sum D(\{y_i\}{i=1}^M, \{z_i\}{i=1}^N; \Theta) \]

来估计两个离散分布之间的距离是符合大数定理的，可以这么搞。

4. GAN就完了

由于$\{z_i\}{i=1}^M$是固定的，变数都在于由$\theta$生成的$\{y_i\}{i=1}^M$序列上，所以先简写为

\[\mathcal{L}=\frac{1}{M}\sum_{i=1}^M D(y_i; \Theta) \]

再回顾一下$D(y_i; \Theta)$和$Y=G(X;\theta)$的定义：

$Y=G(X;\theta)$是指从指定分布$X$中推导目标$Y$的过程；
$D(y_i; \Theta)$是指生成的$Y$与已有样本$Z$之间的距离，由于样本都是离散的，所以通过大量样本的平均距离代替分布之间的距离。

因此，$\mathcal{L}$就是表征两个分布之间的差异程度，可以想象为Entrophy的打分机制，分数越高越表示二者之间的差距越大【1：假】，分数越低表示二者之间的差距越小【0：真】。

$!NOTE$
值得注意的是，1和0并不总代表着真和假，它的含义是人为赋予 的。这点在代码中的损失函数构建中也可见一斑（无论是否加负号，都是成立的）。

根据GAN中生成器G、判别器D的概念，G希望生成得到的样本足够真实，即生成得到的$y_i$输入D中的分数$\mathcal{L}$足够小（当等于0时，完全是真的 ）；而D则希望生成得到的$y_i$输入后得到的分数$\mathcal{L}$足够大（当等于1时，完全可以区分 ），并且希望真实样本$z_i$输入得到的分数$\mathcal{L}$足够小（希望真的可以被识别为真的 ）。因此这里就存在了GAN中Adversarial对抗的含义。

并且也引出训练过程：

1.固定生成器$G(X;\theta)$，生成一批样本$Y$，得到目标函数：

\[\begin{aligned} \Theta &=\mathop{\arg \max} \limits_{\Theta}L_1\\ &=\mathop{\arg \max} \limits_{\Theta}\frac{1}{B}\sum_{i=1}^B[D(y_i,\Theta)-D(z_i,\Theta)] \end{aligned} \]

$!NOTE$
这里的B指的是批次数batchsize，个人理解这是大数定理影响下的无奈妥协之举。

2.固定判别器$D(Y;\Theta)$，通过训练$\theta$使得生成样本越加逼真：

\[\begin{aligned} \theta &=\mathop{\arg \min} \limits_{\theta}L_2\\ &=\mathop{\arg \min} \limits_{\theta}\frac{1}{B}\sum_{i=1}^B[D(G(x_i,\theta),\Theta)] \end{aligned} \]

$!NOTE$

$L_1$是真伪样本分布差（的最大值） ，那么$L_1$越小表示"伪造"样本质量越好，所以$L_1$是表征训练程度的指标，$L_1$越小表示训练的越好；

将$L_1$作为核心指标的原因也和训练过程有关，由于首先需要生成一批样本，所以如果生成器太弱$L_1$过大的话 ，$L_2$会被要求快速的下降 来使得惩罚尽可能的小 ，但是这也可能会导致生成器生成一些重复、保底 的图片，对于训练不是很友好；所以一定程度上要求生成器强一些，$L_1$一开始就比较小，这样才能倒逼 $L_2$不大且往更精细（更小）的方向去；

5. 正则约束---WGAN

如果不给D加上约束，会使得$L_1$值$\rightarrow\infty$，因为$D(z_i,\Theta)$就会变得很小以证明判别器觉得它是真的。

通常来说，可以在最后加上sigmod来使得最终输出约束在$[0,1]$的区间内，但是由于$L_1$值$\rightarrow\infty$，会导致那段的梯度特别小，无法实现梯度的更新。（例如：$x=10$，Sigmoid输出是$0.9999$，导数是$0.0001$。那么$-\nabla_{\theta}D(G(z))$会由于$D(G(z)) \approx 0(1)$而导致梯度无法有效回传）

WGAN从原理出发，通过如下约束：

距离是为了表明两个对象的差距，而如果对象产生微小的变化，那么距离的波动也不能太大。

\[\begin{aligned} \Vert D(y_i,\theta)-D(y^{'}_i,\theta)\Vert &\leq C\Vert y_i-y^{'}_i\Vert^\alpha \\ \Vert D(y_i,\theta)-D(y^{'}_i,\theta)\Vert &\leq C\Vert y_i-y^{'}_i\Vert, \alpha=1 \\ \Vert \frac{\partial D(y,\Theta)}{\partial y}\Vert &\leq C \end{aligned} \]

上述就是常见的Lipschitz（利普西茨）约束，满足这个约束可以整体的稳定性得到提升，不会出现对$y$的一点变动导致距离极大变化的问题（也是在拆东墙补西墙，弥补由神经网络度量距离的问题）

\[\begin{aligned} \Theta&=\mathop{\arg \max}\limits_{\Theta}\frac{1}{B}\sum_{i=1}^B[D(y_i,\Theta)-D(z_i,\Theta)] \\ &=\mathop{\arg \min}\limits_{\Theta}\frac{1}{B}\sum_{i=1}^B[D(z_i,\Theta)-D(y_i,\Theta)] \end{aligned} \]

可以通过把上述利普西茨约束放在$L_1$项中：

\[\begin{aligned} \Theta&=\mathop{\arg \max}\limits_{\Theta}\frac{1}{B}\sum_{i=1}^B[D(y_i,\Theta)-D(z_i,\Theta)]+\lambda \max(\Vert \frac{\partial D(y,\Theta)}{\partial y}\Vert,1) \\ \Theta&=\mathop{\arg \max}\limits_{\Theta}\frac{1}{B}\sum_{i=1}^B[D(y_i,\Theta)-D(z_i,\Theta)]+\lambda (\Vert \frac{\partial D(y,\Theta)}{\partial y}\Vert-1)^2 \end{aligned} \]

后者是WGAN原作者提出的损失函数，通过一个弱正则项对变动起到约束作用。

具体计算时，偏导数通过离散化计算：

\[\begin{aligned} \Theta&=\mathop{\arg \max}\limits_{\Theta}\frac{1}{B}\sum_{i=1}^B[D(y_i,\Theta)-D(z_i,\Theta)]+\frac{\lambda}{B} \sum_{i=1}^B\max( \frac{\vert D(y_{i,1},\Theta)-D(y_{i,2},\Theta)\vert}{\Vert y_{i,1}-y_{i,2} \Vert},1) \\ \Theta&=\mathop{\arg \max}\limits_{\Theta}\frac{1}{B}\sum_{i=1}^B[D(y_i,\Theta)-D(z_i,\Theta)]+\frac{\lambda}{B} \sum_{i=1}^B( \frac{\vert D(y_{i,1},\Theta)-D(y_{i,2},\Theta)\vert}{\Vert y_{i,1}-y_{i,2} \Vert}-1)^2 \end{aligned} \]

其中$y_{i,j}=\epsilon_{i,j}y_i+(1-\epsilon_{i,j})z_i$，$\epsilon_{i,j} \sim U[0,1]$是随机数，$j$表示插值步数，上述为2。

$!NOTE$
对$y_i$和$z_i$中间进行插值生成，也是考虑到真实样本和生成样本之间的连接区域是最有可能违反利普西茨约束 ，也是最有意义对其进行约束的一个范围。

至此，由VAE->GAN->WGAN的序言就结束了。

总体而言，个人理解VAE是一个很优雅，很唯美的哲学对抗，不同于GAN需要先固定生成器优化判别器，再固定判别器优化生成器，直接通过重构＋正则的方式实现了动态对抗；而GAN的意义在于通过神经网络的方式直接把度量的形式都暴力求解出来了，一改往日需要用KL、JS等散度值衡量分布距离的日子；但是GAN由于使用神经网络度量距离会导致违反Lipschitz约束，即对象微小变动导致输入神经网络后距离剧增的现象，因此在判别器$L_1$中引入正则项，使尽可能的遵循该约束。