余同最短路。

最短路我们学过，那同余最短路又是什么东西呢？？可以用来解决什么问题？？往下看。

我们从一道题来得到这个算法的思路。

T494899 硬币问题

正宗的同余最短路

有 $n$ 种面值的硬币（每种有无限枚），问使用这些硬币能够凑出 $[1,m]$ 的多少种金额。$n \le 100,m \le 10^{12},w_i \le 10^6$。

显然这个东西可以使用完全背包做。这样是 $O(nm)$ 的，可是缺点太大。

于是，一个很神奇的解决方法就出现了：同余最短路。

我们观察一个性质：如果对于某一个 $w_i$，如果 $x$ 是可以通过若干面额凑出来的，则 $x+w_i$ 也一定可以凑出来。

所以对于 $x \bmod w_i = d$ 的情况，如果能够找到可以凑出来的 $x$ 的最小值，则就可以通过数学方式计算出 $[1,m]$ 中的所有 $\bmod w_i = d$ 的合法方案数。

具体地，根据左边界可以得出 $x + k \times w_i \ge 1$，根据右边界可以得出 $x + k \times w_i \le m$，其中 $k$ 是一个自然数。

解不等式就可以得出 $k$ 的区间，也可以 $O(1)$ 计算出 $\bmod w_i = d$ 的所有合法方案数。

于是这里的问题就变成了如何找到每种余数下的最小的 $x$。这个时候就需要请出我们的同余最短路了。

考虑到直接对于每一个 $w_i$ 算 $\bmod w_i = d$ 的合法方案数会算重，很麻烦。

不妨直接使用最小的 $w_a$。

可以证明，使用 $\bmod w_a = d (0 \le d < w_a)$ 的一定是全体的答案。很容易证明，也很容易理解。

考虑从举例来理解这个算法的过程。$n=3,m=1000,w=\{3,7,8\}$。

最短路一定是需要建图的。为了便于理解，所以这个时候就建 $8$ 个点 $0$ 到 $7$，表示对 $8$ 的余数。

你应该可以猜到最短路就是什么了，没错就是对于 $8$ 的余数 $0 \le d \le 7$ 的可以凑出来的最小 $x$。

显然 $0$ 的最短路就是 $0$。

虽然这样是不符合条件的因为 $0 \<1$ ，但是为了正确地跑出最短路也只能这样做。为了补救一下，算完最后把答案 $-1$ 即可。

显然对于 $0$ 这个点，有三种选择：加上 $3$、加上 $7$ 或者加上 $8$。

因为 $d \equiv d+8 \ (\bmod 8)$，所以不考虑加上 $8$（这样就会形成自环，反而不好处理）。

而 $0 + 7 \equiv 7 \ (\bmod 8)$，因此存在 $0 \to 7$ 的边权为 $7$。$0 \to 3$ 的边权为 $3$ 同理。

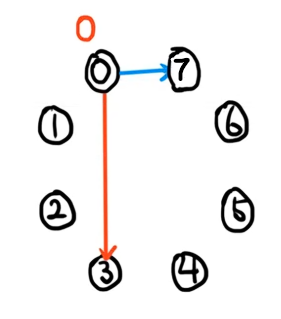
因为这个例子只有两种边，所以这里设边权为 $7$ 的边为蓝边，边权为 $3$ 的边为红边。

把边权为 $3$ 的边连完，就可以得到：

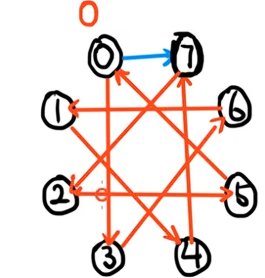
把边权为 $7$ 的边连完，就可以得到：

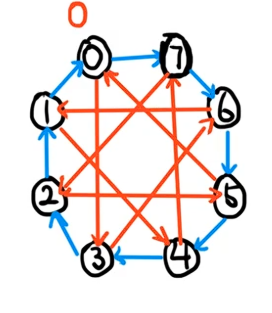
至此所有的边都连完了，于是就可以幸福愉快地跑最短路了。果断选择 dijkstra，因为 $w_i$ 都是正的所以 dijkstra 一定是正确的。

如果有 $w_i$ 是负数，就只能另想办法了。

dijkstra 的过程这里不再阐述，最后跑出来就是这个结果：

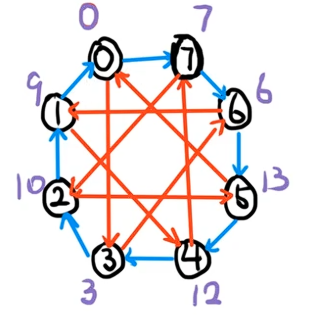
目测可以发现，除去 $0$ 以外，其他所有点得出来的结果都是正确的！

总结一下，算出来所有余数的最小能够凑出来的面值的过程为：

先建出 $[0,w_a -1]$ 的所有点。
对于每一个点 $x$，对于 $1 \le i \le n$，连边 $x \to (x + w_i) \bmod w_a$。
设 $dis_0$ 为 $0$。以 $0$ 为源点跑 dijkstra，最终的 $dis$ 值就是每一个余数的最小面值（$0$ 除外，$dis_0$ 理应当是 $w_a$），采用数学方式就可以算出来最终的结果。

于是就做完了。这里的东西只和 $w_i$ 和 $n$ 有关，而 $w_i$ 的范围是不大的，和 $m$ 没有半毛钱关系。

建出来的图有 $w_a \approx 10^6$ 个点，一共有 $O(w_a \times n) \approx O(10^8)$ 条边。

如果存图还是太占用空间了，于是考虑直接无实物建图 ，因为每一条边的起点和终点都是很有规律的。复杂度应该是 $O(n \log n + m)$ 的，可以跑过去，但还是有一些慢，毕竟 $m \approx 10^8$ 嘛。

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
#define N 1000010
int n, w[N];
int dis[N], m;
bool vis[N];

void Dijkstra(int start) {
	priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
	for (int i = 0; i < w[1]; ++i)
		dis[i] = 1e17, vis[i] = 0;
	dis[start] = 0;
	q.push({0, start});
	while (q.empty() == 0) {
		auto [tmp, u] = q.top();
		q.pop();
		if (vis[u] == 1)
			continue;
		else
			vis[u] = 1;
		for (int i = 2; i <= n; ++i) {
			int v = (u + w[i]) % w[1];
			if (vis[v] == 0 && dis[v] > dis[u] + w[i]) {
				dis[v] = dis[u] + w[i];
				q.push({dis[v], v});
			}
		}
	}
}

signed main() {
	ios::sync_with_stdio(0);
	cin >> n >> m;
	for (int i = 1; i <= n; ++i)
		cin >> w[i];
	sort(w + 1, w + n + 1);
	Dijkstra(0);
	int ans = 0;
	for (int i = 0; i < w[1]; ++i)//为了节省时间，所以采用最小的 w_1
		if (dis[i] < 1e17 && dis[i] <= m)
			ans += (m - dis[i]) / w[1] + 1;
	cout << ans - 1 << endl;
	return 0;
}

注意，这种方法只是解决同余最短路问题的解法中的一种。还有另一种方法，比想象中的要简单。

转圈背包

转圈背包还是一种背包，容易想到，可能是完全背包的优化版本。

于是试图使用完全背包来计算 $dis_i$。

于是我们思考，在同余 $w$ 的情况下，另外一个物品 $w_a$ 最多用几次（假设所有 $w_a$ 已经对 $w$ 取模）。根据数学，显然是 $w / \gcd(w,w_a) - 1$（$w / \gcd{w,w_a}$ 是环的长度，这是一个经典的数学结论）。

于是这就从一个完全背包换成了一个多重背包。

当我们画出来状态转移的有向图的时候：

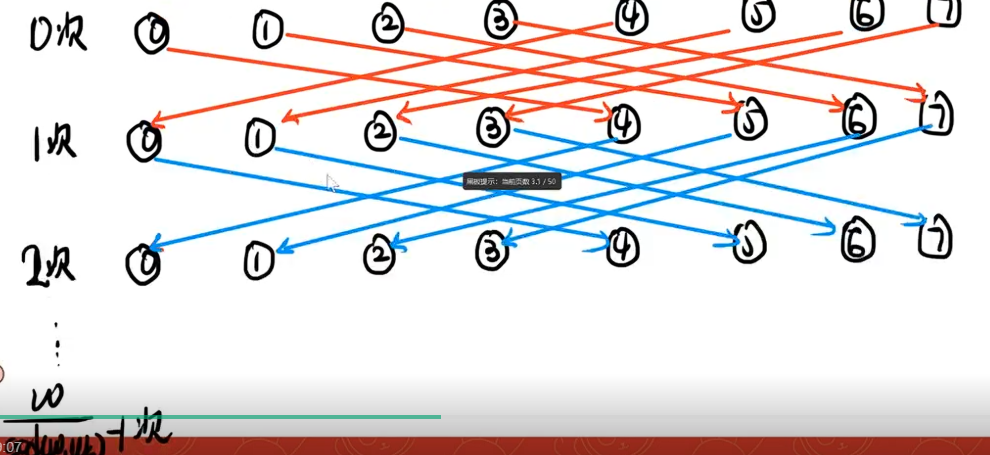
于是就可以类似转圈地进行 dp 了。

但是我们发现，这东西你会超过限制吧？对于单个物品，就一共需要转移 $w \times \frac{w}{\gcd(w,w_a)}$ 次。

整合起来，最多就需要跑 $n \times w^2$ 的量级，显然是不可以接受的。

于是！就需要请出我们重量级的转圈背包了。

考虑假设一个例子，假设 $w = 8$，而 $w_a = 2$。

则很容易提取到其中的一个 $4$ 元环：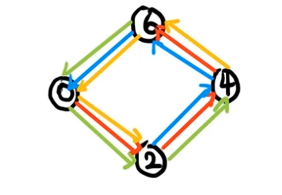

我们发现每一条边都被走了 $3$ 次，而共有 $4$ 条边，也就是一共转移了 $3 \times 4 = 12$ 次。这也是它慢的原因。

接下来，我们需要做一个模型的转化，这个转化超级简单。

我们将其转化为：从 $0$ 开始，先转移一遍。然后（不同的点）再绕整个环一遍进行转移。

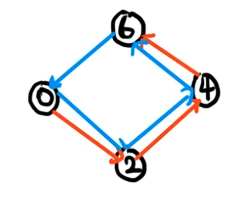
因为转移 $4$ 次和转移 $0$ 次的效果一模一样，所以这样是正确的。

所以，更上面的图片的转移次数为 $w \times (\frac{w}{\gcd(w,w_a)}-1)$，但是下面的这张图片转移次数大约为 $2w$。

所以拼起来就是 $O(n \times \min\{w_i\})$ 的。勉强能够过去这道题。

代码还是很好写的。

cpp 复制代码

#include<bits/stdc++.h>
using namespace std; 
#define int long long
#define N 1001000
int t,n,m,w[N],dp[N];
int cal(int dis,int x) {return (dis <= x) ? (x - dis) / w[1] + 1 : 0;}//计算
int circle(int l,int r)
{
    sort(w + 1,w + n + 1);//物品一定要从小到大考虑
    memset(dp,0x3f,sizeof(dp));
    dp[0] = 0;//dp[i] 表示模 w[1] 为 i 的情况下，最小能够凑出来的金额

    for(int i = 2;i <= n;++i)//依次考虑物品 w[2] to w[n]
        for(int st = 0,up = __gcd(w[i],w[1]) - 1;st <= up;++st)//刚好 0 ~ __gcd(w[i],w[1]) - 1 能够作为每一个环的起点
//枚举每一个环的起点
            for(int u = st,c = 0;c < 2;c += (u == st)) {//c 表示走过了起点多少次，用来统计转圈的圈数
                int v = (u + w[i]) % w[1];//计算要转移的位置
                dp[v] = min(dp[v],dp[u] + w[i]);//转移
                u = v;
            }
        
    int ans = 0;
    for(int i = 0;i < w[1];i++) ans += cal(dp[i],r) - cal(dp[i],l - 1);//计算得到答案
//cal(x,y) 表示从 1 到 y 有多少个数对 w[1] 取模和 x 同于
    return ans;
}
signed main()
{
    ios::sync_with_stdio(false);

    cin >> n >> m;
    for(int i = 1;i <= n;++i) cin >> w[i];
    cout << circle(1, m) << endl;

    return 0;
}