本文发布于博客园,会跟随补题进度实时更新,若您在其他平台阅读到此文,请前往博客园获取更好的阅读体验。
跳转链接:https://www.cnblogs.com/TianTianChaoFangDe/p/18822660
开题 + 补题情况
今天打完蓝桥杯,还是 ACM 赛制好玩啊~~
这场题相对而言比较简单,也是汲取了上次的教训,做题节奏放慢了,稍微细心了点,打出了历史最佳战绩,虽然还是不小心 WA 了两发。

1001 - 烤羊
签到题,枚举调料的使用,可以使用二进制枚举,注意选取的不能超过目的值。
点击查看代码(赛时代码写得依托)
cpp
void solve()
{
i64 k, a, b, c;std::cin >> k >> a >> b >> c;
if(a == k || b == k || c == k) {
std::cout << 0 << '\n';
return;
}
if(a + b == k || b + c == k || a + c == k) {
std::cout << 0 << '\n';
return;
}
if(a + b + c == k) {
std::cout << 0 << '\n';
return;
}
if(a + b + c < k) {
std::cout << k - a - b - c << '\n';
return;
}
auto get = [&](i64 x) -> i64 {
if(x > k)return inf64;
return k - x;
};
i64 ans = inf64;
if(a + b + c > k) {
ans = std::min(ans, get(a));
ans = std::min(ans, get(b));
ans = std::min(ans, get(c));
ans = std::min(ans, get(a + b));
ans = std::min(ans, get(a + c));
ans = std::min(ans, get(b + c));
ans = std::min(ans, get(a + b + c));
if(ans == inf64)ans = k;
std::cout << ans << '\n';
return;
}
}1003 - 抹茶
连续区间贪心选取,很明显的双指针题。
点击查看代码
cpp
void solve()
{
int n;std::cin >> n;
std::vector<i64> a(n + 1), b(n + 1);
for(int i = 1;i <= n;i ++) {
std::cin >> a[i];
}
for(int i = 1;i <= n;i ++) {
std::cin >> b[i];
}
i64 ans = 0;
for(int i = 1, j = 0;i <= n;i = j + 1) {
while(j + 1 <= n && a[j + 1] + b[j + 1] == a[i] + b[i]) {
j ++;
}
i64 tmp = 0;
for(int k = i;k <= j;k ++) {
tmp += a[k] * (j - i + 1);
}
ans = std::max(ans, tmp);
}
std::cout << ans << '\n';
}1007 - 双相
要想最大,肯定是优先选最大的,将两种颜色的分数分别放入两个优先队列,然后模拟选取,直到选不了一人无法移动为止。
点击查看代码
cpp
void solve()
{
int n;std::cin >> n;
std::vector<i64> a(n + 1);
std::string s;
for(int i = 1;i <= n;i ++)std::cin >> a[i];
std::cin >> s;
s = ' ' + s;
std::priority_queue<i64> r, b;
for(int i = 1;i <= n;i ++) {
if(s[i] == 'R') {
r.push(a[i]);
} else {
b.push(a[i]);
}
}
i64 ans = 0;
int sum = 0;
while(true) {
sum ++;
if(sum & 1) {
if(!r.size()) {
break;
}
ans += r.top();
r.pop();
} else {
if(!b.size()) {
break;
}
ans += b.top();
b.pop();
}
}
std::cout << ans << '\n';
}1008 - 天使
对于此题,我们可以先将范围缩小,假设只有三个使徒,考虑他们的结合顺序,不难发现:
\[a \times b + (a + b) \times c = a \times c + (a + c) \times b = b \times c + (b + c) \times a \]
因此,不管怎么结合,最后的答案都不会变化,结合后的又可以和其他的进行结合,那么,把这个结论推广到 \(n\) 个使徒同样成立。
因此不管怎么结合,最后的答案都一样。
所以,我们只需要从左到右结合算出答案,然后用 \(\sum_{i = 2}^n C_i^2\) 算出种类数即可。
点击查看代码(省略了取模类)
cpp
Z C(Z n) {
return n * (n - 1) / 2;
}
void solve()
{
int n;std::cin >> n;
std::vector<i64> a(n + 1);
for(int i = 1;i <= n;i ++)std::cin >> a[i];
Z ans = 0;
Z now = a[1];
for(int i = 2;i <= n;i ++) {
ans += now * a[i];
now += a[i];
}
Z sum = 1;
for(int i = n;i >= 2;i --) {
sum *= C(i);
}
std::cout << ans << ' ' << sum << '\n';
}1002 - 英逃
首先需要观察出答案是具有单调性的。
为什么?
假设修改区间 \([l, r]\) 是可以达到题目要求的,那么对于 \([l - 1, r]\),可以分析以下两种情况(区间 \([l, r + 1]\) 同理):
- \(a_{l - 1} \geq \max_{i = l}^ra_i\)(如下图,黑色为修改前,红色为修改后,下同):
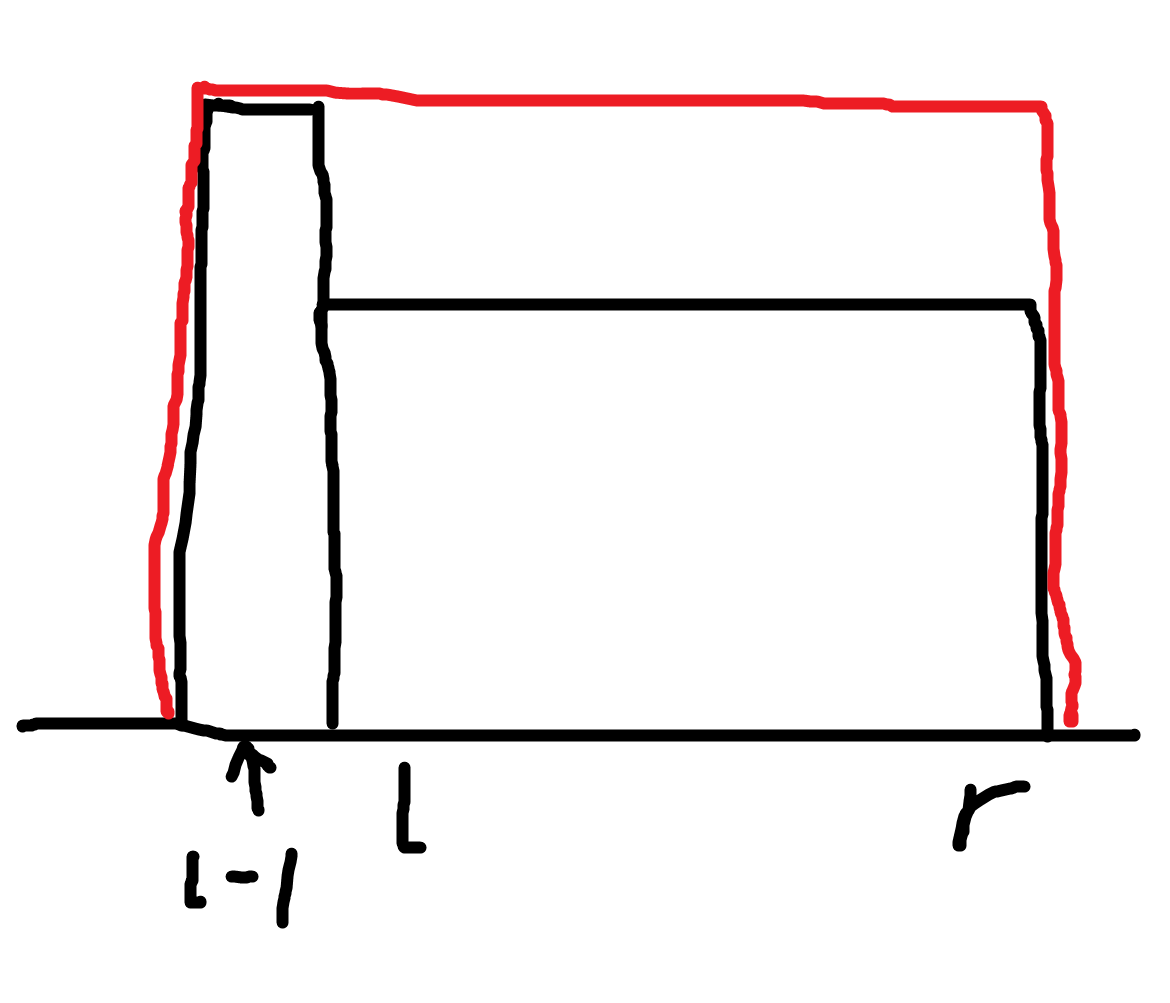
对于区间 \([l, r]\),它们对代价的贡献无变化,仍为 \(0\),但对于左边这个新增的 \(a_{l - 1}\),由于相邻两个数的差值变为了 \(0\),因此对代价的贡献变小了,那么如果修改区间 \([l, r]\) 能达到题目目的,修改区间 \([l - 1, r]\) 同样能达到题目目的。 - \(a_{l - 1} < \max_{i = l}^ra_i\),此时继续分两种情况讨论:
- \(a_{l - 2} \leq a_{l - 1}\)(如下图):
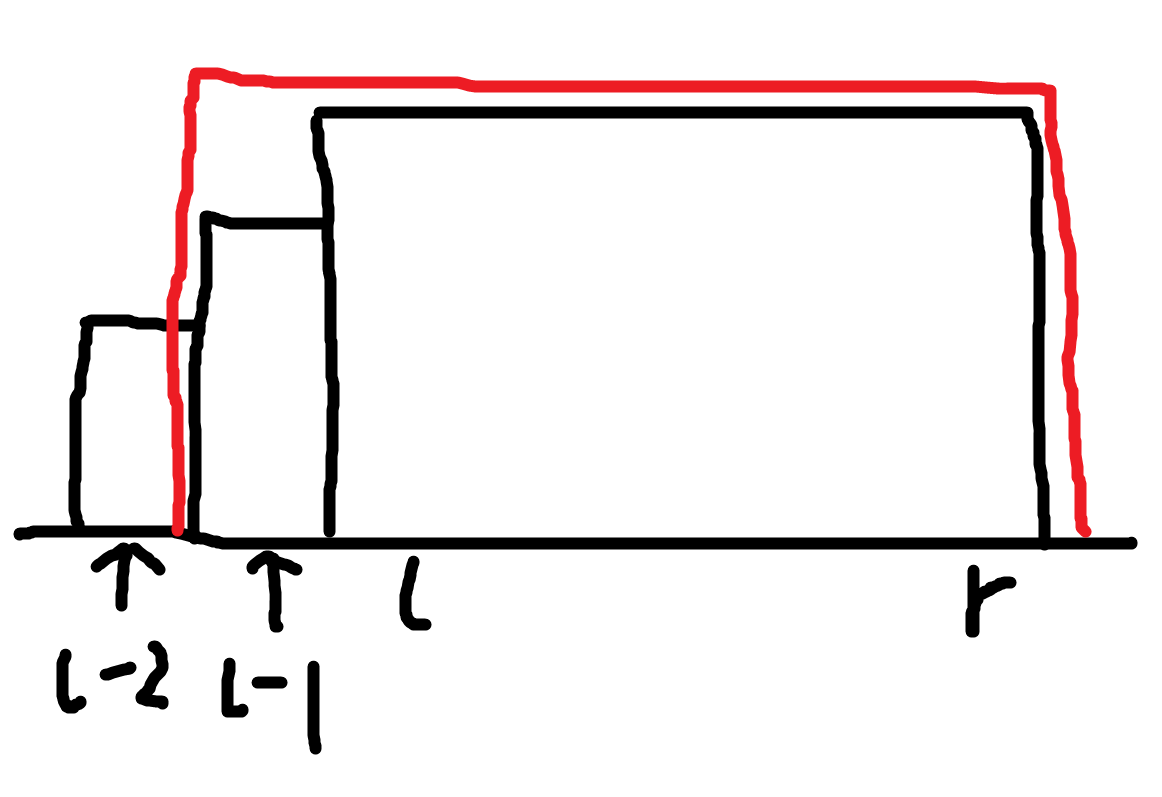
对于这种情况,我们可以发现,\(a_{l - 1}\) 和 \(\max_{i = l}^ra_i\) 的差值缩小了 \(\max_{i = l}^ra_i - a_{l - 1}\),\(a_{l - 1}\) 和 \(a_{l - 2}\) 的差值增大了 \(\max_{i = l}^ra_i - a_{l - 1}\),因此对代价的贡献无变化,那么如果修改区间 \([l, r]\) 能达到题目目的,修改区间 \([l - 1, r]\) 同样能达到题目目的。 - \(a_{l - 2} > a_{l - 1}\)(如下图):

对于这种情况,我们可以发现,\(a_{l - 1}\) 和 \(\max_{i = l}^ra_i\) 的差值缩小了 \(\max_{i = l}^ra_i - a_{l - 1}\),\(a_{l - 1}\) 和 \(a_{l - 2}\) 的差值缩小了 \(\max_{i = l}^ra_i - a_{l - 1}\),因此对代价的贡献缩小了 \(2 \times (\max_{i = l}^ra_i - a_{l - 1})\),那么如果修改区间 \([l, r]\) 能达到题目目的,修改区间 \([l - 1, r]\) 同样能达到题目目的。
- \(a_{l - 2} \leq a_{l - 1}\)(如下图):
因此,答案具有单调性,可以二分。
我们首先记录一下差分的绝对值以及差分的绝对值的前缀和,使用 ST 表来维护区间最值,然后进行二分答案,对每个二分到的区间长度,遍历所有可能的修改区间,更改修改后的代价总和,判断是否可能达到题目要求,在所有可能的答案中取最小即可。
点击查看代码
cpp
void solve()
{
int n;
i64 x;
std::cin >> n >> x;
std::vector<i64> a(n + 1);
for(int i = 1;i <= n;i ++)std::cin >> a[i];
std::vector<i64> d(n + 1);
for(int i = 2;i <= n;i ++) {
d[i] = abs(a[i] - a[i - 1]);
}
std::vector<i64> pre(n + 1);
for(int i = 2;i <= n;i ++) {
pre[i] = pre[i - 1] + d[i];
}
if(pre[n] <= x) {
std::cout << 0 << '\n';
return;
}
std::vector<std::array<i64, 40>> st(n + 1);
for(int i = 1;i <= n;i ++) {
st[i][0] = a[i];
}
int mx = std::__lg(n);
for(int k = 1;k <= mx;k ++) {
for(int i = 1;i + (1 << (k - 1)) <= n;i ++) {
st[i][k] = std::max(st[i][k - 1], st[i + (1 << (k - 1))][k - 1]);
}
}
auto getmx = [&](int l, int r) -> i64 {
int s = std::__lg(r - l + 1);
return std::max(st[l][s], st[r - (1 << s) + 1][s]);
};
auto check = [&](i64 m) -> bool {
i64 tmp = pre[n];
for(int i = 1;i <= n - m + 1;i ++) {
tmp = pre[n];
tmp -= pre[i + m - 1] - pre[i];
if(i != 1)tmp -= abs(a[i] - a[i - 1]);
if(i + m - 1 != n)tmp -= abs(a[i + m] - a[i + m - 1]);
i64 mx = getmx(i, i + m - 1);
if(i != 1)tmp += abs(mx - a[i - 1]);
if(i + m - 1 != n)tmp += abs(a[i + m] - mx);
if(tmp <= x)return true;
}
return false;
};
int l = 0, r = n + 1;
while(l + 1 < r) {
int mid = l + r >> 1;
if(check(mid))r = mid;
else l = mid;
}
std::cout << r << '\n';
}1010 - 章鱼
这题是很明显的换根 DP。
首先我们考虑一下,当一个点是一对点的 \(LCA\) 时,什么样的点对的 \(LCA\) 是它。
- 自己和自己的 \(LCA\) 都是自己。
- 对于这个点,它的子树(不包含父节点那个子树)中任选两个子树,两个子树中各自任选一个点,\(LCA\) 是它自己。
- 对于这个点,从它的子树(不包含父节点那个子树)中任选一个点,和这个点的 \(LCA\) 是它自己。
那么,思路也就出来了,对于每个结点为 \(LCA\) 时,逐个计算,当一个结点作为根时,除了根所在的这棵子树,对其他的子树按上述规则进行计数,对于每一棵子树,无论这棵子树哪个结点作为根,计算得到的答案都是相同的,因为都相当于是把这棵子树变成了父子树,这棵子树的结点都不可能和任何结点的 \(LCA\) 是当前结点。
换根 DP 足以解决这个问题。
点击查看代码
cpp
void solve()
{
int n;std::cin >> n;
std::vector<std::vector<int>> g(n + 1);
for(int i = 1;i < n;i ++) {
int u, v;std::cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
std::vector<int> sz(n + 1);
auto dfs = [&](auto &&self, int st, int pre) -> void {
sz[st] = 1;
for(auto &i : g[st]) {
if(i == pre)continue;
self(self, i, st);
sz[st] += sz[i];
}
};
dfs(dfs, 1, 0);
std::vector<i64> ans(n + 1);
auto C = [](i64 n) -> i64 {
return n * (n - 1) / 2;
};
auto dfs1 = [&](auto &&self, int st, int pre) -> void {
int n = g[st].size();
std::vector<i64> szpre(n + 1), Cpre(n + 1);
for(int i = 1;i <= n;i ++) {
if(g[st][i - 1] == pre)szpre[i] = szpre[i - 1] + sz[1] - sz[st];
else szpre[i] = szpre[i - 1] + sz[g[st][i - 1]];
if(g[st][i - 1] == pre)Cpre[i] = Cpre[i - 1] + C(sz[1] - sz[st]);
else Cpre[i] = Cpre[i - 1] + C(sz[g[st][i - 1]]);
}
for(int i = 1;i <= n;i ++) {
ans[st] += (szpre[i] - szpre[i - 1]) * (C(szpre[i - 1] + szpre[n] - szpre[i]) - (Cpre[i - 1] + Cpre[n] - Cpre[i]));
ans[st] += (szpre[i] - szpre[i - 1]) * (szpre[i - 1] + szpre[n] - szpre[i]);
}
ans[st] += sz[1] - 1;
ans[st] += C(szpre[n]) - Cpre[n];
for(auto &i : g[st]) {
if(i == pre)continue;
self(self, i, st);
}
};
dfs1(dfs1, 1, 0);
for(int i = 1;i <= n;i ++) {
ans[i] += sz[1];
std::cout << ans[i] << " \n"[i == n];
}
}