技术背景

QUBO(Quadratic Unconstrained Binary Optimization)模型是一种常用于求解组合优化问题的一种技术，它所能够求解的问题是这样定义的：给定一个布尔类型的数组：

\[x=[x_1, x_2, x_3, ..., x_n]^T, x_i\in\{0,1\} \]

以及一个相同维度的\(Q\)矩阵，对于\(Q\)矩阵有：\(Q_{ij}=Q_{ji}\)，也就是一个实对称矩阵。然后可以得到一个总体的损失函数：

\[y=x^TQx \]

而QUBO模型的求解，就是找到使得损失函数值\(y\)最小的一组\(x_t\)，作为问题的最终解。如果把矩阵形式的QUBO函数展开，可以写为：

\[x_t=\mathrm{argmin}\ y=\sum_iQ_{ii}x_i+\sum_{i,j}Q_{ij}x_ix_j \]

也就是说，只要问题能够被定义成这种形式，那么就都可以通过QUBO的相关求解器，或者是物理机来进行求解。关于物理机求解的部分，往往通过一个线性变换转换为Ising模型进行求解。Ising模型对应的自变量为：

\[x=[x_1, x_2, x_3, ..., x_n]^T, x_i\in\{-1, 1\} \]

然后求解：

\[x_t=\mathrm{argmin}\ y=\sum_ih_ix_i+\sum_{i,j}J_{ij}x_ix_j \]

关于QUBO模型的求解方法，第一种方案是直接在变量空间中进行遍历搜索，直到找到一个合适的解。但是由于QUBO模型的解空间可以大到\(2^n\)大小，随着变量的增长而指数增长，暴力搜索可能并不是一个最有效的方法。更加promising的一种方式是使用物理机器，构建整个解空间的量子叠加态，通过变分的方法去优化基态能量，最终在本征态附近去搜索最优解：

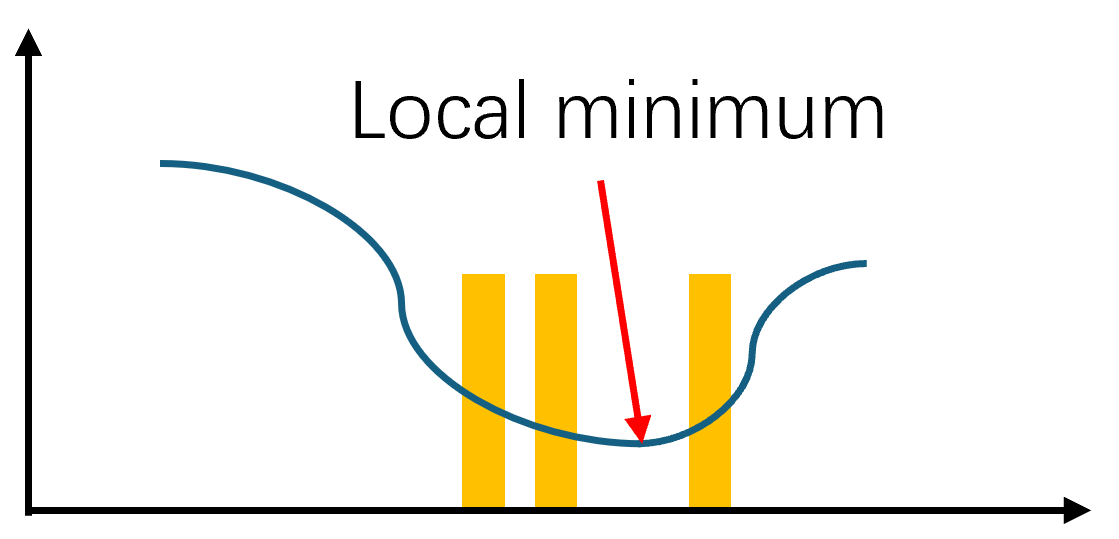
因为量子态的解空间是连续的，因此本征态附近往往对应的Solution State也对应比较低的能量或者Cost。在了解了QUBO模型的求解方案之后，还有一个非常至关重要的问题，那就是如何把我们所需要求解的问题映射到QUBO模型上，这是本文要着重进行介绍的内容。核心内容来自Fred Glover(Tabu Search禁忌搜索的提出者)的一篇综述文章，加上一些我的个人理解和示例的具象化。

数字分配问题

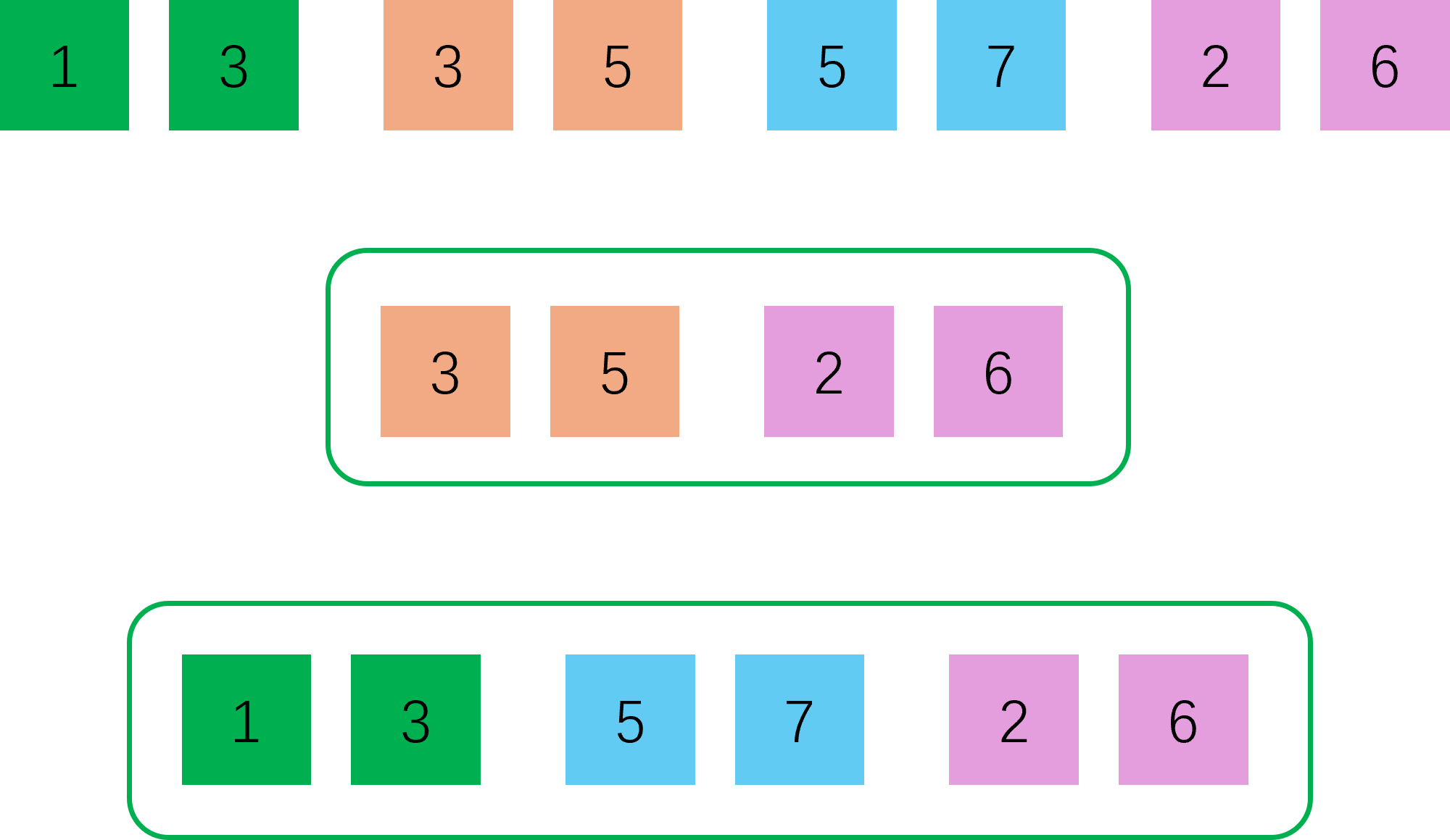
Number Partitioning是一个比较好理解的经典问题：我们有一组数字，现在要把这组数字分为两组，使得分割之后的两组数字的总和最接近。

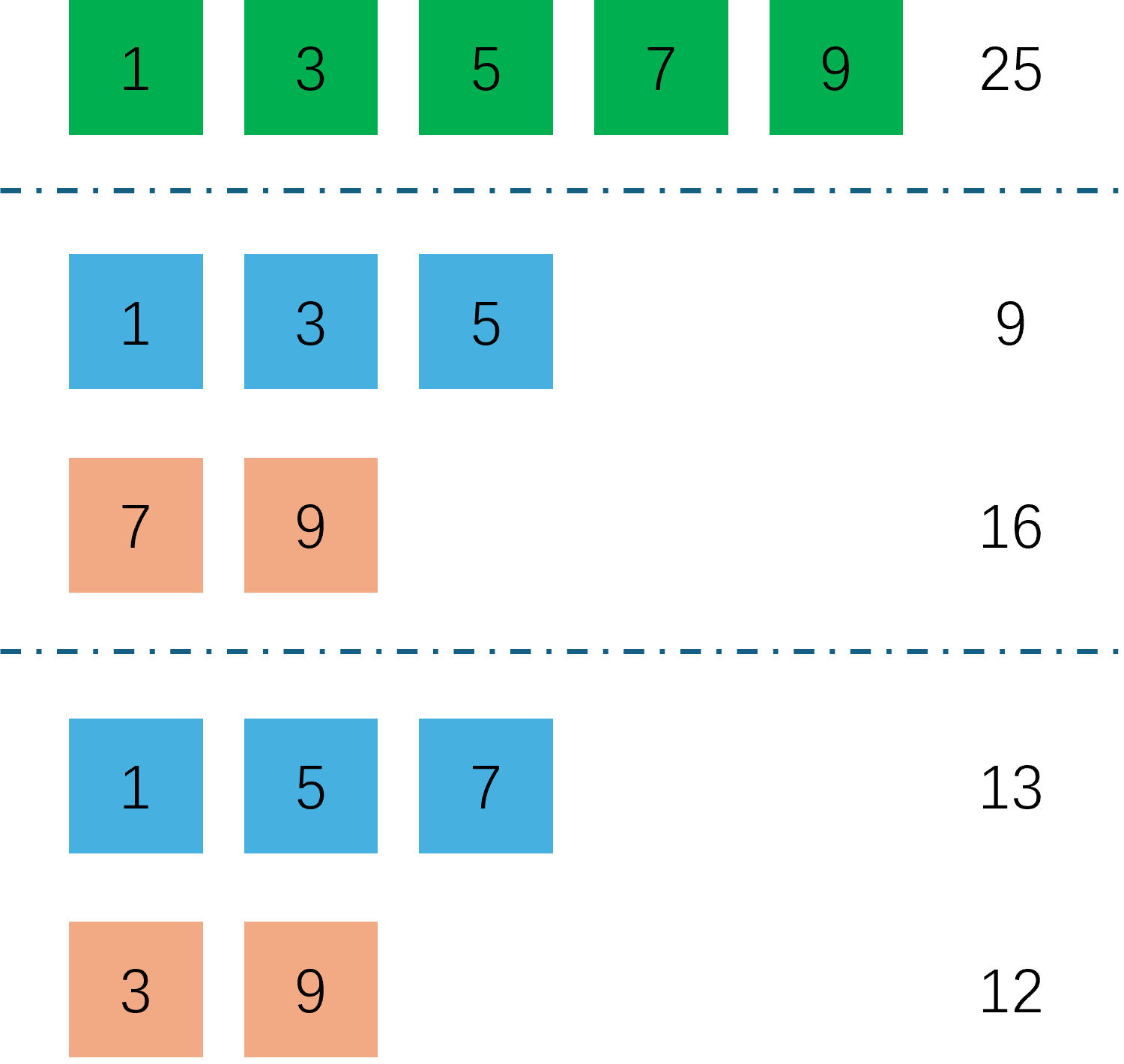
在上面这个示意图中，最上面一排绿色的数字表示待分配的数字组合，下面提供了两种分配方案。第一种分配方案两组数总和的差距为7，第二种分配方案数字总和的差距为1，那么第二种分配方案显然就是一种更好的选择。在理解清楚这个问题之后，接下来要考虑如何使用QUBO模型对这个问题进行建模。首先我们用一个数组\(V\)来记录原始数字的值：

\[V=\{v_1, v_2, v_3, ..., v_m\} \]

然后用一个布尔数组来记录对应编号的数字被分配到第一个组合里面还是第二个组合里面：

\[X=\{x_1, x_2, x_3, ..., x_m\}, x_i\in\{0, 1\} \]

如果定义\(x_i=1\)时，\(v_i\)被分配到第一个集合中，那么第一个集合最终的数字总和就是：

\[S_1=\sum_iv_ix_i \]

第二个数字组合的总和就是：

\[S_2=-S_1+\sum_iv_i \]

可以得到两个数字组合的总和差值为：

这个总和差值，也就是我们需要优化的目标函数。对于这种绝对值形式的目标函数，我们可以直接取一个平方值作为QUBO模型的模型函数：

\[Y=\left(2\sum_iv_ix_i-C\right)^2=4\sum_iv_i^2x_i^2+4\sum_{i,j}v_iv_jx_ix_j-4C\sum_iv_ix_i+C^2 \]

因为对于\(x_i\)来说有：\(x_i^2=x_i\)，因此QUBO模型函数也可以写为：

\[Y=4\sum_i(v_i^2-Cv_i)x_i+4\sum_{i,j}v_iv_jx_ix_j \]

可以得到\(Q\)矩阵的对角元为：

\[Q_{ii}=4v_i^2-4Cv_i \]

又因为QUBO模型的\(Q\)矩阵是一个对称矩阵，因此非对角元为：

\[Q_{ij}=Q_{ji}=2v_iv_j \]

有了\(Q\)矩阵，就完成了数字分配问题的QUBO建模，后续的工作就是交给求解器或者是Ising机/物理机来完成了。

最大切割问题

Max Cut最大切割问题，是一个图论中的典型问题。问题定义是比较简单的，给定一个无向图\(G(V,E)\)，将所有的节点分为两个集合，使得连接两个集合的边数量最多。

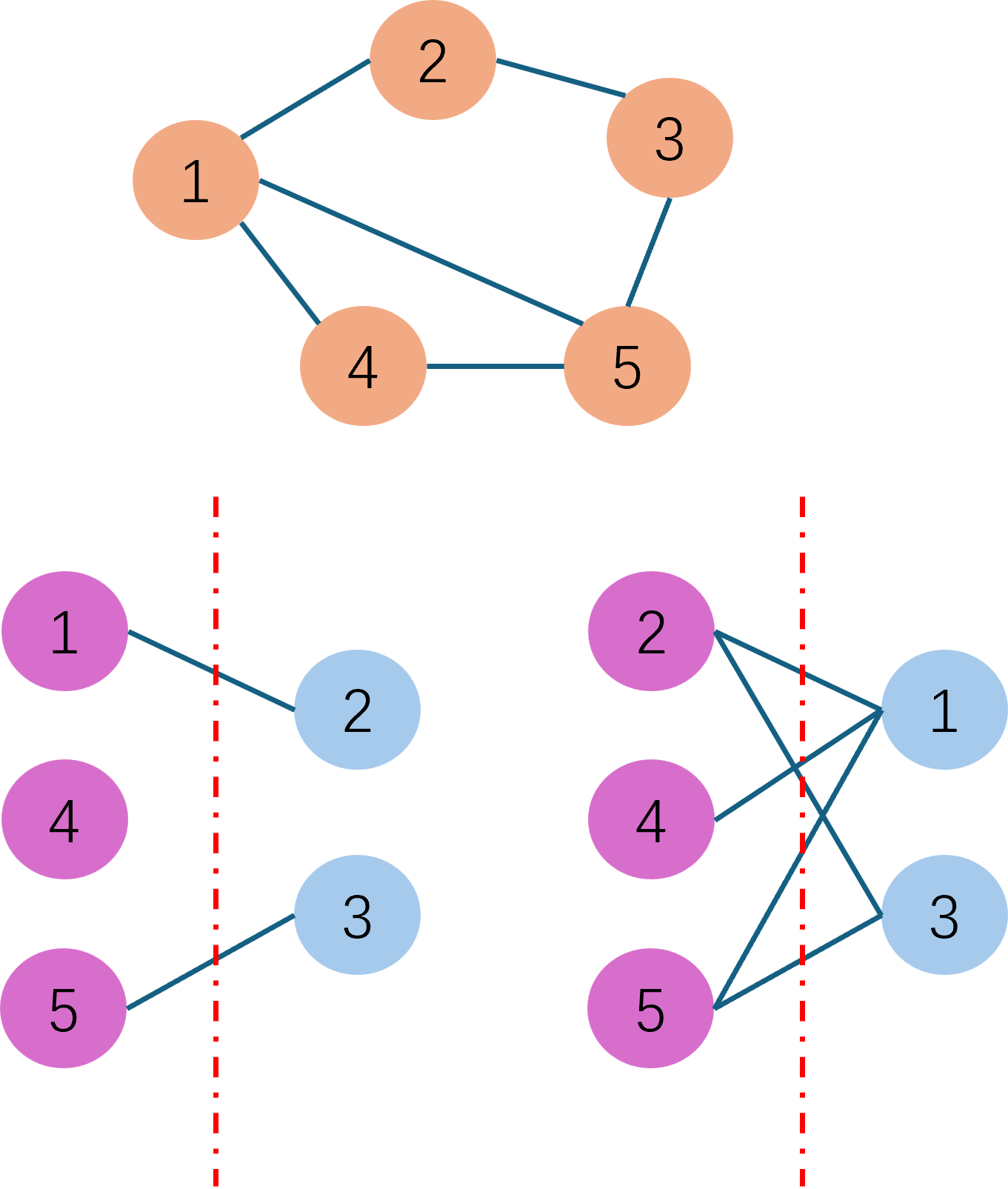
例如上图中的黄色节点，就是原始给定的无向图。如果把该无向图的节点按照左下角的示例分成\(\{1,4,5\}\)和\(\{2,3\}\)两个集合，那么连接两个集合的边的数量是2。如果按照右下角的示例分成\(\{2,4,5\}\)和\(\{1,3\}\)，那么连接两个集合的边的数量就是5，明显是一个更好的分配方案。理解清楚问题定义之后，我们可以用QUBO模型来对该问题进行建模。首先定义节点信息和边信息：

\[V=\{v_1, v_2, v_3, ..., v_m\}\\ E=\{e_1, e_2, e_3, ..., e_n\}, e_i=(v_{ji}, v_{ki}) \]

在定义一个布尔数组，用于判定节点被分配到哪个集合中：

\[X=\{x_1, x_2, x_3, ..., x_m\}, x_i\in\{0,1\} \]

如果\(x_i=0\)，则表示节点\(v_i\)被分配到了第1个集合中，如果\(x_i=1\)，则表示节点\(v_i\)被分配到第2个集合中。完成这些定义后，我们可以数值化的表达Max Cut问题的目标函数：

\[y=\sum_{(v_i,v_j)\in E}x_i+x_j-2x_ix_j \]

这个目标函数的特点是，我们对所有的边进行遍历，如果一条边所连接的两个节点被分配到两个集合中，得到的值是1，如果两个节点被分配到同一个集合中，这个函数值是0。所以，如果我们最大化这个目标函数，就等同于最大化连接两个集合的边的数量。但是因为在求解QUBO问题时，我们通常只能对目标函数做最小化，因此需要加上一个负号，使目标函数变为一个最终的QUBO模型函数：

\[Y=\sum_{(v_i,v_j)\in E}2x_ix_j-x_i-x_j \]

注意到\(\sum_{(v_i,v_j)\in E}x_i\)这一项，其实是在数节点\(v_i\)的近邻数量，所以我们可以根据边的信息预先计算一个近邻数量数组：

\[N=\{n_1, n_2, n_3, ..., n_m\} \]

那么结合QUBO的模型函数，我们可以得到\(Q\)矩阵的对角元为：

\[Q_{ii}=-n_i \]

非对角元为：

\[Q_{ij}=Q_{ji}=1, (v_i,v_j)\in E \]

得到\(Q\)矩阵之后，就可以代入求解器或者物理机进行求解了。

最少节点覆盖问题

跟最大切割问题有点类似，最少节点覆盖也是一个图论问题。给定一个无向图\(G(V,E)\)，只保留一部分节点，但要求剩下的节点能够覆盖到所有的边，求最少的节点保留数量和方案。

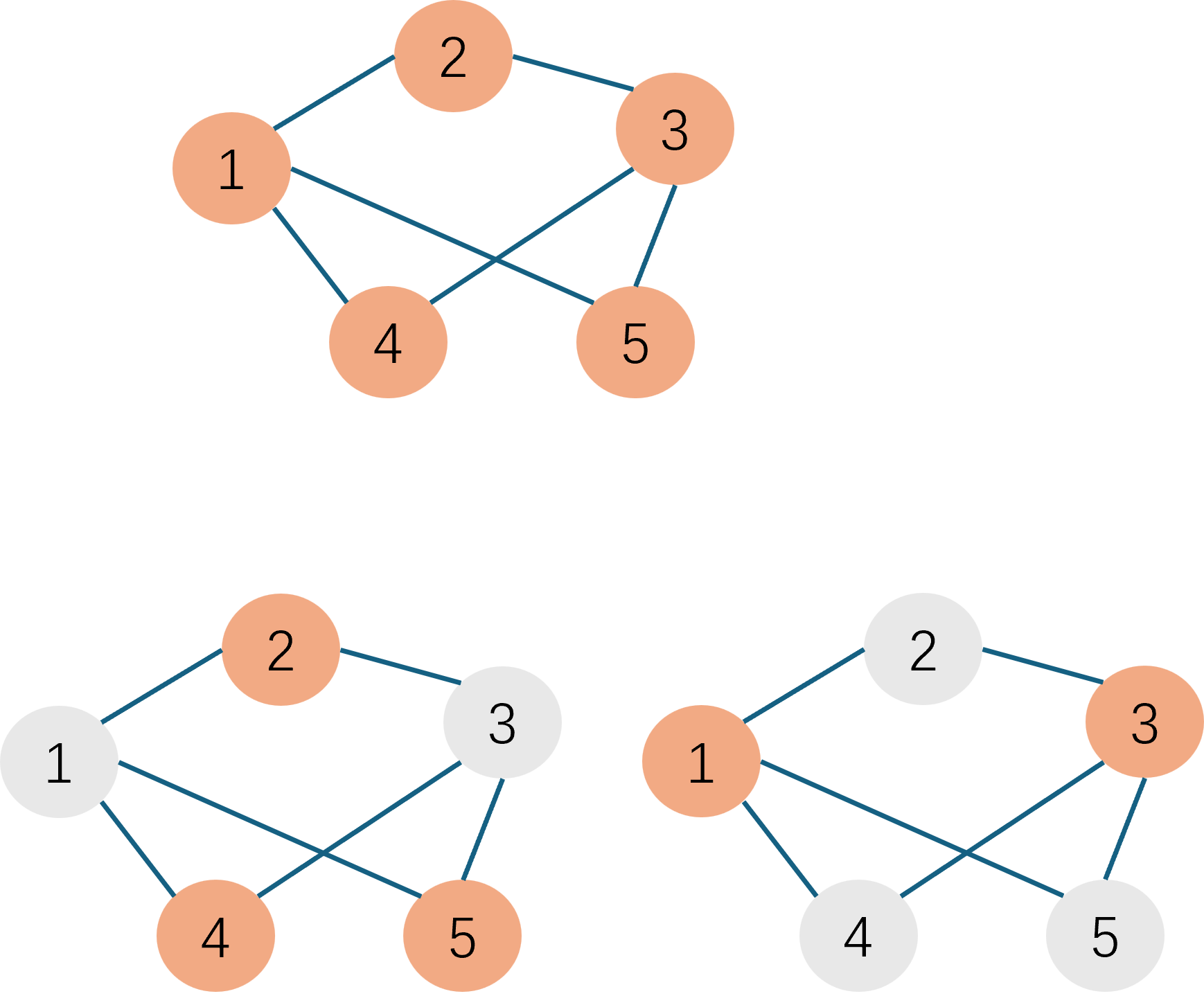
就像上面这个图中，最原始的有5个节点。假如按照左下角的方案，我们只保留2，4，5这三个节点，可以看到所有的边都有被覆盖到，那么这个节点保留方案是一个可行解。但如果是按照右下角的节点保留方案，只保留1，3两个节点，我们发现所有的边也都有被覆盖到，那么这就是一个更好的方案。接下来要给出这个问题的QUBO建模形式。首先我们还是给定无向图的节点信息和边信息：

\[V=\{v_1, v_2, v_3, ..., v_m\}\\ E=\{e_1, e_2, e_3, ..., e_n\}, e_i=(v_{ji}, v_{ki}) \]

此时我们定义一个节点是否保留的布尔数组：

\[X=\{x_1, x_2, x_3, ..., x_m\}, x_i\in\{0,1\} \]

这里如果\(x_i=1\)表示节点\(v_i\)被保留下来，如果\(x_i=0\)，那就说明\(v_i\)没有被保留下来。这样我们保留下来的节点数就是：

\[y=\sum_ix_i \]

但需要注意的是，此时还要考虑这样的一个约束条件：

\[\prod_{(v_i,v_j)\in E}(x_i+x_j)>0 \]

这个约束条件是说，对于所有的边，至少有一个节点被保留下来了，否则就不是一个可行解。按照常规的搜索求解方案，我们就是对解空间进行遍历，找到所有的可行解，再从可行解中查找\(y\)最小的解作为最终解。但是这样求解的效率太低了，我们可以考虑把这个硬约束条件转化成一个软约束条件，变成一个QUBO形式的函数，这样我们就可以使用QUBO模型来进行求解。只要软约束条件定义的好，我们也可以使得最终的解大概率满足硬约束条件。这里采用的软约束条件，是一个类似于最大切割问题的约束：

\[Y=\sum_ix_i+P\sum_{(v_i,v_j)\in E}\left(1-x_i-x_j+x_ix_j\right) \]

这里引入了一个惩罚值\(P,P>0\)，这是一个经验性的参数。而后面这个惩罚项的意义是，如果\(x_i=x_j=0\)，也就是有一条边的两个节点都不被保留的情况，此时的惩罚值为\(P\)。如果存在\(q\)条这样的边，那么惩罚值就会是\(qP\)。而如果其中有一个值是1，也就是\(x_i=1\or x_j=1\)，那么惩罚值计算出来是0。因此，只要我们最小化\(Y\)，理想条件下，最终可以把惩罚项优化到0，就可以得到\(Y=y\)的优化后的可行解。如果此时定义每个节点的近邻节点数量为：

\[N=\{n_1, n_2, n_3, ..., n_m\} \]

那么可以写出最少节点覆盖问题的QUBO模型的\(Q\)矩阵对角元素：

\[Q_{ii}=1-n_iP \]

非对角元为：

\[Q_{ij}=Q_{ji}=0.5P, (v_i,v_j)\in E \]

完成\(Q\)矩阵元素计算之后，就可以代入求解器或者物理机进行求解了。

集合封装问题

Set Packing集合封装问题，也可以从无向图的角度来理解。我们先假定一个集合里面只能有2个元素，那么一个集合就相当于一条边。给定一张图\(G(V,E)\)，最后只保留一些边，注意这里保留的不是节点了。我们的目标是使得最后被保留下来的边的数量最大化，这就是一个简单版的集合封装问题了。对于更加广义的集合封装问题，往往一个集合对应着很多条边，那么优化的目标就是使得保留下来的集合的数量尽可能的多，而不是边的数量尽可能的多了。当然，这里有一个约束条件是，同一个节点在最终被保留下来的集合的集合中，最多只能出现一次。也就是说，如果一个节点出现在多个边或者多个集合中，最终可以被保留下来的边或者集合只能在其中最多选一个。我们可以看一个图来更加直观的理解：

在原始的集合中，1号节点和3号节点可以构成一个集合，3号节点又和5号节点可以构成一个集合。虽然这里展示的集合中都只有2个节点，但是对于更加广义的集合封装问题，这里的集合中可以有多个的节点。为了满足约束条件，我们可以有两个集合保留的方案。第一个方案我们保留3,5和2,6这两个集合，其他的集合都不能再保留下来了，因为会有节点冲突。而第二个方案我们保留下来了1,3、5,7和2,6这三个集合，显然是一个更好的方案。接下来用QUBO模型对这个问题进行建模，首先定义节点和集合：

\[V=\{v_1, v_2, v_3, ..., v_m\}\\ S=\{s_1, s_2, s_3, ..., s_n\}, s_i=(v_{ji}, v_{ki}, ..., v_{li}) \]

假如第\(i\)个节点出现在第\(j\)个集合中，我们定义一个二维的元素：

\[a_{ij}=1,v_i\in s_j \]

反之有：

\[a_{ij}=0,v_i\notin s_j \]

不同于最少节点覆盖问题，这里我们要定义的布尔数组是以集合为单位的：

\[X={x_1, x_2, x_3, ..., x_n}, x_i\in\{0,1\} \]

其中\(x_i=1\)时我们说第\(i\)个集合要被保留下来。这样我们就可以定义出最终需要保留的集合的总数：

\[y=\sum_ix_i \]

我们的最终目标就是使得\(y\)最大化，但同时要满足约束条件：

\[\sum_ja_{ij}x_j\leq 1 \]

这个约束条件表示：遍历所有被保留的集合，第\(i\)个节点最多只能出现1次。那么我们可以用反向思维来进行QUBO建模，设立一个惩罚项，用于惩罚一个节点在多个被保留的集合中出现的次数：

\[Y=-\sum_ix_i+P\sum_i\left(\sum_{j,k}a_{ij}a_{ik}x_jx_k\right) \]

通过最小化\(Y\)的值，理想条件下使得惩罚项的值为0，即可得到我们所需要的\(y\)的最大值。这个QUBO模型对应的\(Q\)矩阵的对角元素为：

\[Q_{ii}=-1 \]

非对角元为：

\[Q_{jk}=Q_{kj}=0.5P\sum_ia_{ij}a_{ik} \]

完成\(Q\)矩阵元素计算之后，就可以代入求解器或者物理机进行求解。

最大可满足性问题

相比于前面的几个问题，Max 2-Sat最大可满足性问题，理解起来会相对比较抽象一点。首先是literal，这个概念其实就是一个命题，不同于前面提到的图论中的节点，命题可以被clause所包含，命题的否同样也可以作为一个命题被clause所包含。这里的clause是多个命题的或，在Max 2-Sat问题中，一个clause里面有两个literal，只要其中的一个literal成立，那么这个clause就成立。最终的优化目标，就是给定literal的值，使得尽可能多的clause成立。下图是一个简单的Max 2-Sat示例：

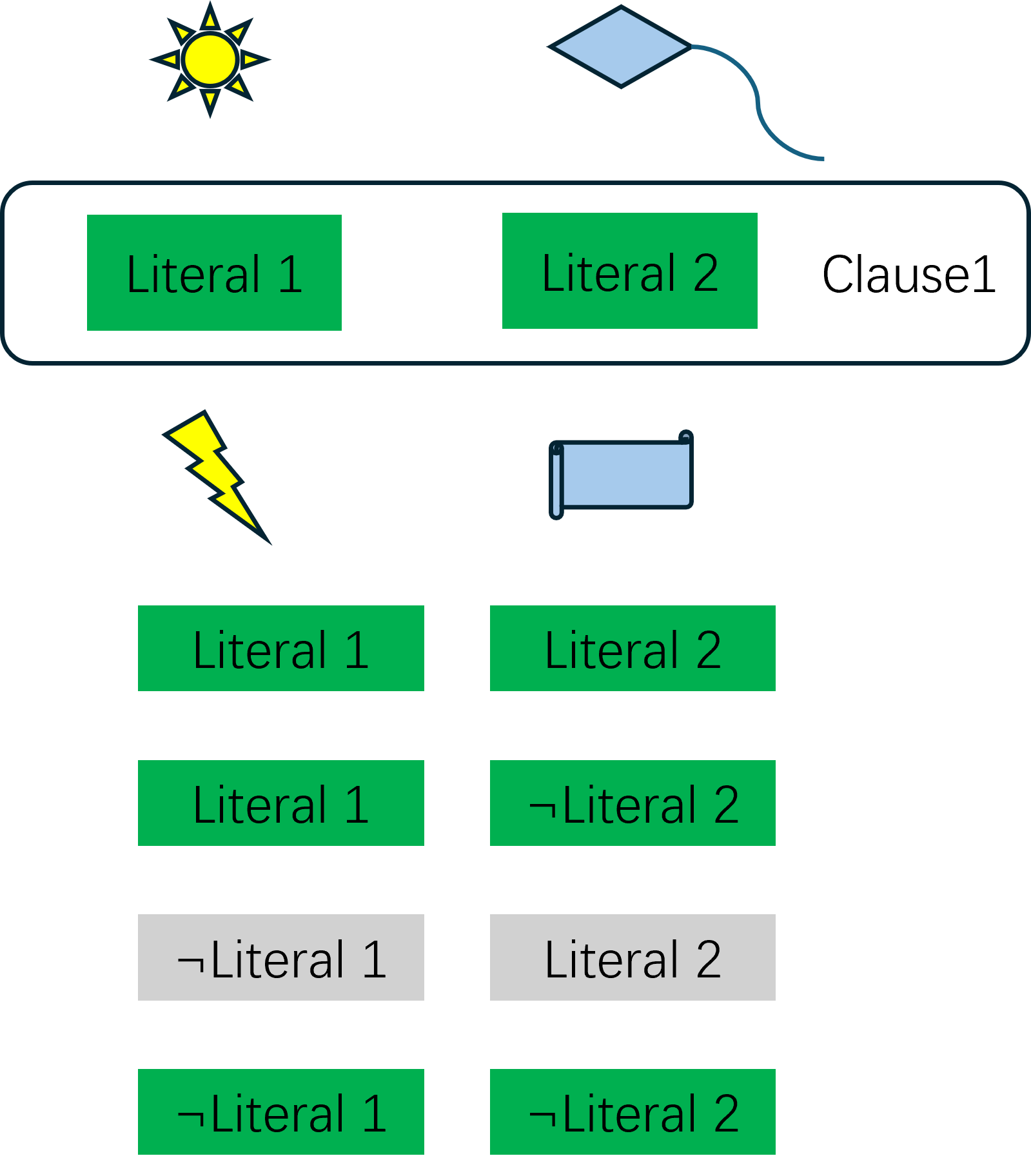
假如我们在做一个形成规划，literal1用来表示天气，literal1为True时表示出太阳，literal1为False时，或者literal1的否为True时，表示打雷下雨。而literal2为False时，表示出门放风筝，literal2为True或者literal2的否为False时，表示在家里看书。这样的话两个literal之间就有了一定的关联性，如果把这两个literal组成一个clause，那么就不能让它出现打雷的同时出门放风筝，也就是两个literal都是False这样的情况。当然，这样理解起来可能还是会有点抽象，建议还是直接看建模的部分。首先我们定义一系列literal的值：

\[L=\{l_1, l_2, l_3, ..., l_m\}, l_i\in\{0,1\} \]

还有一系列的二元clause：

\[C=\{c_1, c_2, c_3, ..., c_n\} \]

前面提到，literal本身和literal的否都可以存在于clause中，因此我们需要定义两个二维的变量用于标记literal在clause中的位置：

\[a_{ij}=1,l_i\in c_j;a_{ij}=0,l_i\notin c_j;b_{ij}=1,\neg l_i\in c_j;b_{ij}=0,\neg l_i\notin c_j \]

然后用一个布尔数组用于表示clause是否成立：

\[X=\{x_1, x_2, x_3, ..., x_n\}, x_i\in\{0, 1\} \]

类似于集合封装和最少节点覆盖问题，我们需要优化的目标还是数数量，不过是数clause的数量：

\[y=\sum_ix_i \]

但是这里有两个约束条件。第一个约束条件，因为我们是2-Sat问题，因此一个clause中最多只能存在2个literal：

\[\sum_ia_{ij}c_j+b_{ij}c_j=2 \]

但是这个约束条件不一定会体现在最终的惩罚函数中（跟使用的惩罚函数有关系）。第二个约束条件是最终被保留下来的clause一定是成立的：

\[\prod_{k}\left[a_{ik}l_i+a_{jk}l_j+b_{ik}(1-l_i)+b_{jk}(1-l_j)\right]x_k\geq 1 \]

换句话说，存在于clause \(c_k\)中的两个literal至少有一个是True的。如果从逆向的思维来考虑，我们希望至少有一个literal为True，那么就惩罚所有的literal都是False的这种情况：

\[Y=-\sum_ix_i+P\sum_k\left[a_{ik}a_{jk}(1-l_i)(1-l_j)+a_{ik}b_{jk}(1-l_i)l_j+b_{ik}a_{jk}l_i(1-l_j)+b_{ik}b_{jk}l_il_j\right]x_k \]

在这个形式的惩罚函数中，虽然我们没有显式的包含第一个约束条件，但其实已经排除了所有literal数量不为2的情况。那么根据上述函数，可以得到QUBO模型的\(Q\)矩阵的对角元为：

\[Q_{ii}=\sum_k(-a_{ik}a_{jk}+b_{ik}a_{jk}) \]

非对角元为：

\[Q_{ij}=Q_{ji}=0.5P\sum_k(a_{ik}a_{jk}-a_{ik}b_{jk}-b_{ik}a_{jk}+b_{ik}b_{jk}) \]

完成\(Q\)矩阵元素计算之后，就可以代入求解器或者物理机进行求解。

集合划分问题

Set Partitioning集合划分问题，其实是一个典型的任务调度和分配问题，是一个日常生活中很常见的一个问题种类。如下是一个示例：

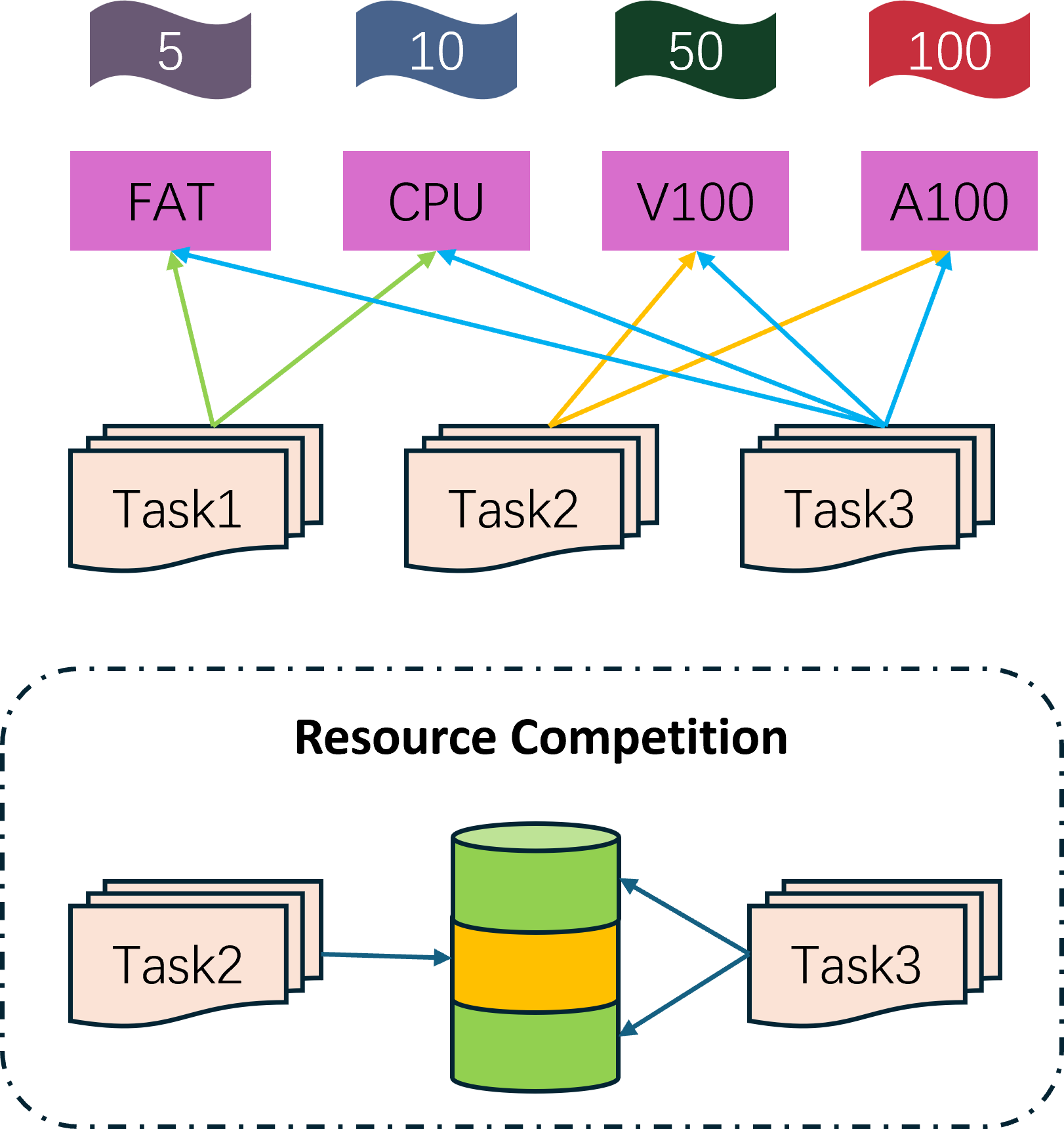
这是一个超算集群的任务提交问题，任务一可以提交到胖节点或者CPU节点进行计算，任务二可以提交到有GPU的节点进行计算，任务三在几种类型的节点上都能算。但是不同的节点的耗费是不一一的，因此我们要找到一种分配的方案，使得总体的耗费最少。当然，真实场景里面我们必须要考虑到一个任务间的资源竞争问题，而这里我们仅讨论最简单的这部分任务分配的问题。先定义一系列的集群对应的费用：

\[C=\{c_1, c_2, c_3, ..., c_m\} \]

再定义一系列的待执行任务：

\[T=\{t_1, t_2, t_3, ..., t_n\} \]

有了集群和任务，可以再定义一个二维的数组，用于标记任务所处的集群，例如：

\[a_{ij}=1,t_i\in c_j, a_{ij}=0, t_i\notin c_j \]

这里的记法非常的不规范，能够理解\(a_{ij}\)这个参数表示的含义即可。然后定义一个布尔数组用于标识集群是否被使用到：

\[X=\{x_1, x_2, x_3, ..., x_m\}, x_i\in\{0, 1\} \]

这样总体的任务计算费用为：

\[y=\sum_i c_ix_i \]

我们的目标就是最小化任务的总体资金耗费。且这里需要满足一个约束条件：

\[\sum_ja_{ij}x_j=1 \]

这个约束条件表示的是，每一个任务都被调度了至少一次。像这种用等号来表述的约束条件是最好处理的，直接使用等号两边的差值平方做惩罚函数即可：

\[Y=\sum_i c_ix_i+P\sum_i\left(\sum_ja_{ij}x_j-1\right)^2 \]

通过展开这个目标函数，我们可以得到QUBO模型的\(Q\)矩阵对角元：

\[Q_{ii}=c_i+P\sum_ja^2_{ji}-2P\sum_ja_{ji} \]

非对角元为：

\[Q_{ij}=Q_{ji}=P\sum_ka_{ki}a_{kj} \]

完成\(Q\)矩阵元素计算之后，就可以代入求解器或者物理机进行求解。

图着色问题

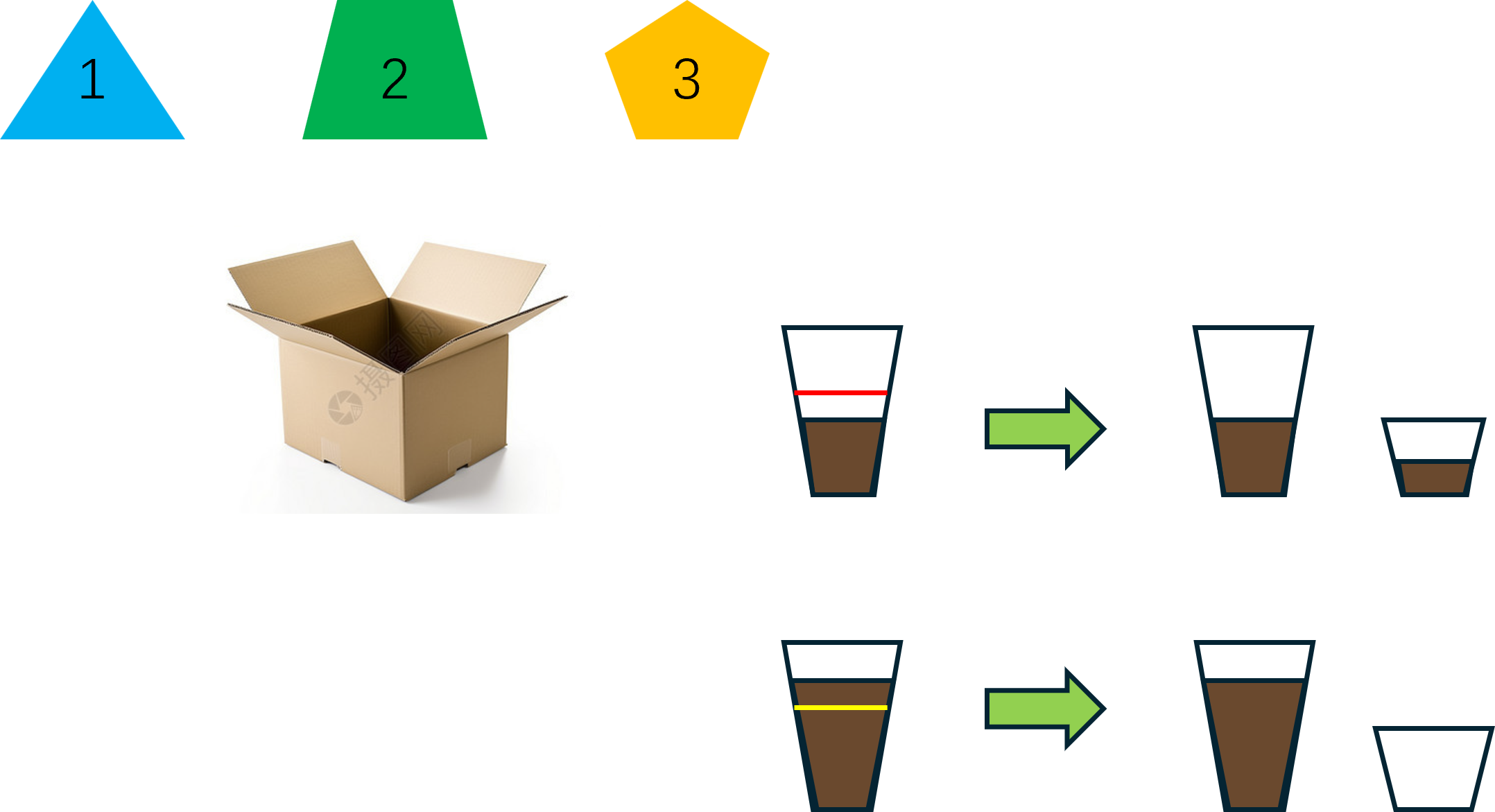
Graph Coloring图着色问题，问题本身是比较好理解的。给定一个无向图\(G(V,E)\)，要在每个节点上涂一个颜色，要求是每一条边所连接的两个节点不能涂同一种颜色，然后求解颜色使用最少的一个方案。就像下面这个示例：

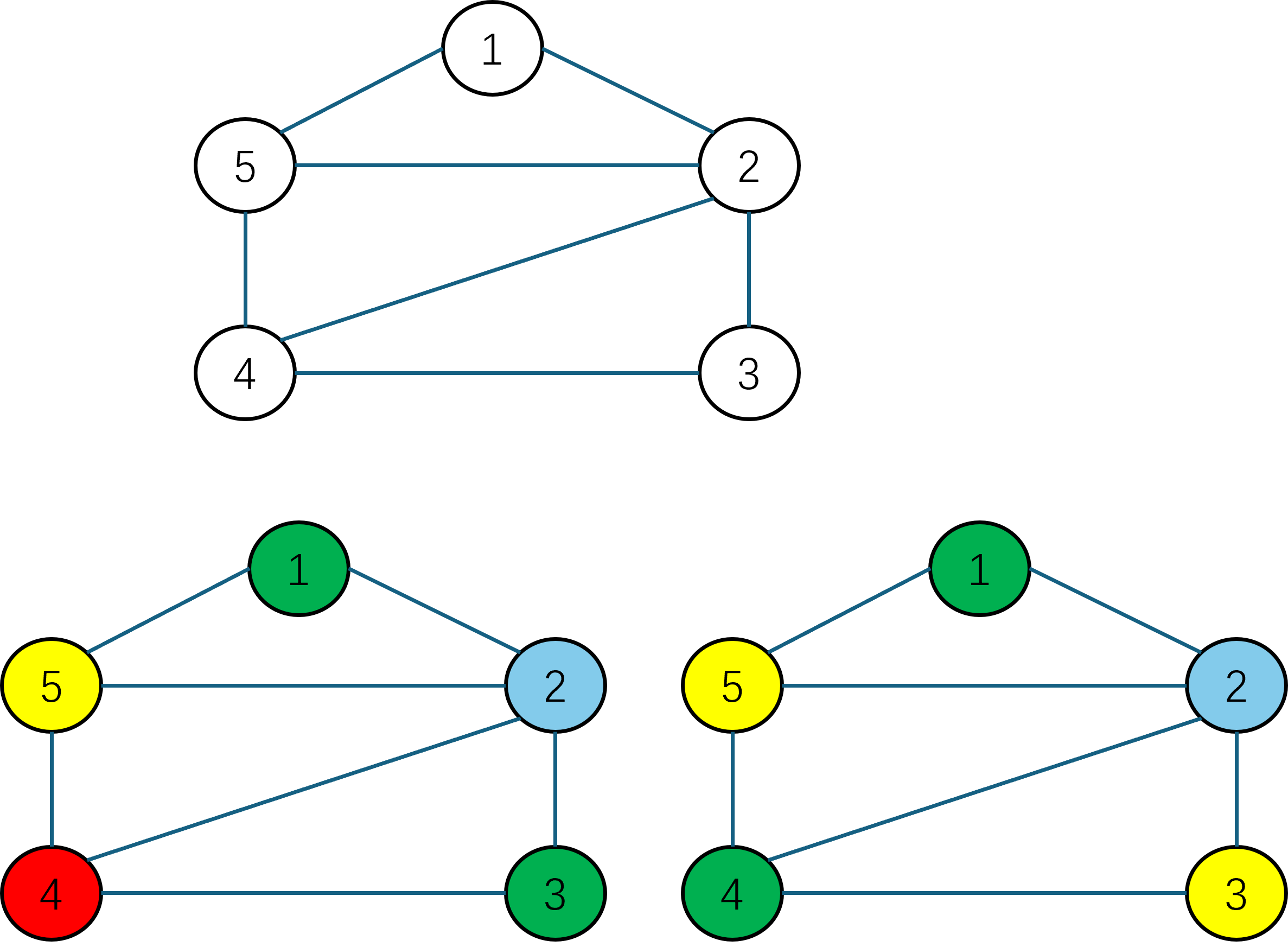
对于这个示例图，我们给出了两种不同的着色方案。左边的方案用了4种不同的颜色，右边的方案使用了3种不同的颜色。两个着色方案都满足同边不同色的要求，但是右边使用的颜色数量更少，是一个更好的方案。不过这里图着色问题与四色问题不同的是，图着色问题不需要去证明颜色数量的普适性，我们只需要针对给定的颜色数量，给出一个可行的着色方案即可。那么我们可以首先定义节点和边：

\[V=\{v_1, v_2, v_3, ..., v_m\}\\ E=\{e_1, e_2, e_3, ..., e_n\} \]

另外还需要定义一个颜色的集合：

\[C=\{c_1, c_2, c_3, ..., c_p\} \]

有了颜色和节点的定义，可以再定义一个二维数组用于标记节点所使用的颜色：\(x_{ij}=1\)表示第\(i\)个节点涂上了第\(j\)种颜色，而\(x_{ij}=0\)表示第\(i\)个节点没有涂上第\(j\)种颜色。假定在一个没有任何约束的情况下，是有可能出现一个节点着多种颜色或者没有着任何颜色的情况，那么我们就需要通过使用约束条件来避免这种情况的出现：

\[\sum_{(v_j,v_k)\in E}(x_{ij}+x_{ik})\leq 1,\sum_jx_{ij}=1 \]

第一个条件表示同一个颜色在每一条边连接的两个节点上出现的次数最多1次，可以避免一条边连接同一种颜色的可能性，类似于Max 2-Sat中的约束条件。第二个条件表示每一个节点只能涂一种颜色，类似于Set Partitioning中的约束条件。那么我们就可以给出一个相对应的惩罚值函数：

\[Y=P\sum_i\sum_{(v_j,v_k)\in E}x_{ij}x_{ik}+P\sum_i\left(\sum_jx_{ij}-1\right)^2 \]

由于\(x_{ij}\)是一个二维的数组，而QUBO模型所能够求解的是一维的数组，因此这里可以将\(x_{ij}\)展开成一维进行求解，定义：

\[z_f=z_{(i-1)m+j}=x_{ij} \]

那么对应于一维的布尔数组\(Z\)，可以计算其QUBO模型的\(Q\)矩阵的对角元：

\[Q_{ii}=-P \]

需要注意的是，这里的对角元索引\(i\)是已经展开成一维之后的情况。这个案例比较特殊的是，它的\(Q\)矩阵的非对角元可以分成两个部分：着色非对角部分和节点非对角部分。这是因为我们对二维的\(x\)数组进行了展开，因此最终的结果会是一个块对角矩阵，例如参考文献1中给出的一个案例：

这部分非对角元素的值为：

\[Q_{ij}=Q_{ji}=P \]

而节点间的相互作用其实是块跟块之间的相互作用，因此会是一系列的对角矩阵块，同样的可以参考下参考文献一中的示例：

节点间作用项的非对角元为：

\[Q_{ij}=Q_{ji}=0.5P \]

完成\(Q\)矩阵元素计算之后，就可以代入求解器或者物理机进行求解。

广义0-1规划问题

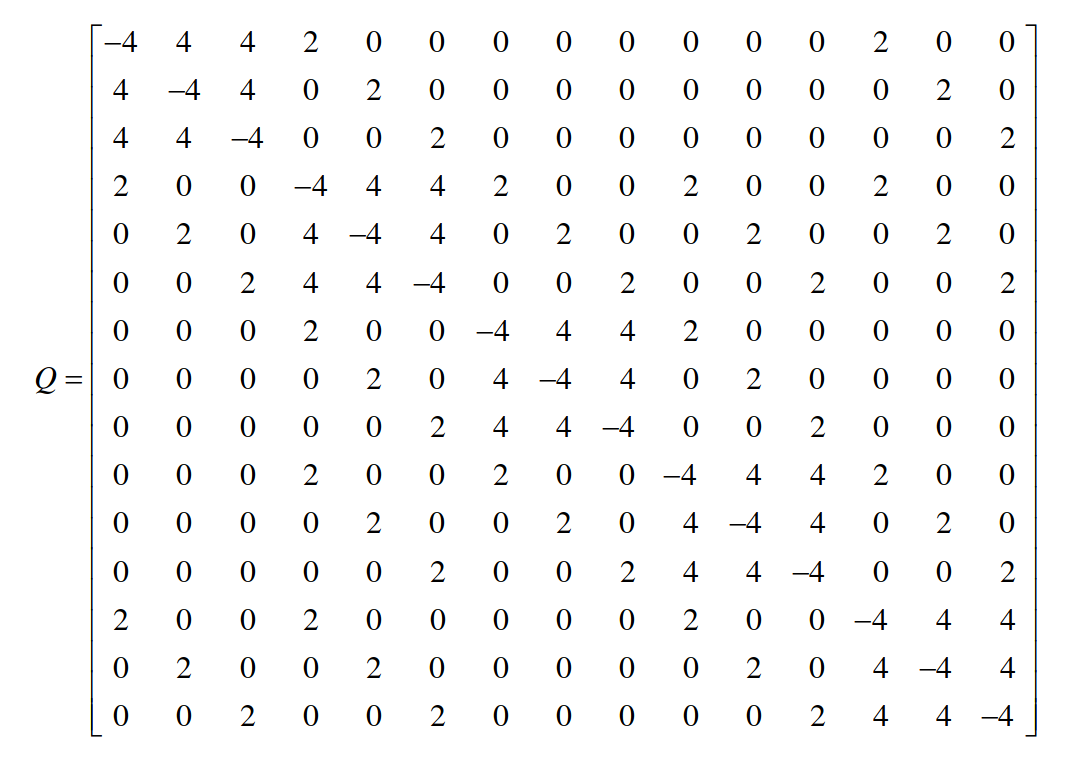
General 0-1 Programming广义0-1规划问题，其实可以包含上面的大多数问题。简答的理解就是有一个需要最小化的损失函数，再加上一系列不同形式的约束条件，这样的问题都可以使用广义0-1规划问题的求解框架来进行求解。最典型的0-1规划问题是这个背包问题：假如我们有一系列的物品，每个物品都有自己的价值和重量，而背包的载重量是有限的，所以我们需要在背包承重范围内装入尽可能价值高的物品。这里就有一个问题了，如果是限制总重量等于某个值，那问题是比较容易建模的，直接参考Set Partitioning的这种约束条件设立一个二次的惩罚值即可。但这里我们要求的是装载物品的重量小于某个值，有些其他场景下可能是大于某个值。对于这种不等式约束条件的建模，就是广义0-1规划问题所需要解决的一个问题。我们先来看一个示例：

左上角就是一个经典的背包问题了，这里我们不直接对背包问题进行展开介绍，但是我们会用到它的目标函数。给定一系列的物品，它们的价值和重量分别为：

\[V=\{v_1, v_2, v_3, ..., v_m\}\\ C=\{c_1, c_2, c_3, ..., c_m\} \]

最后决定是否将这个物品装进背包的布尔数组为：

\[X=\{x_1, x_2, x_3, ..., x_m\},x_i\in\{0,1\} \]

那么背包问题的目标函数为：

\[y=\sum_i v_ix_i \]

需要满足的约束条件为：

\[\sum_ic_ix_i\leq U \]

这里的\(U\)就是背包的承重量了。不过这里我们只是借用一下背包问题的约束条件和目标函数，因为我们要将这个问题推广到一个更加通用的场景。对于更加通用的广义0-1规划问题，其约束条件为：

\[\sum_ic_ix_i\leq U\\ \sum_im_ix_i=N\\ \sum_id_ix_i\geq L\\ \]

此时再回头解释一下上面图中右下角两个图的含义。如果我们要装一杯咖啡，要求咖啡的量必须要低于杯子上的红线，也就是第一种约束条件的形式。但是这种形式的约束没办法直接用到最终的目标函数中，除非可以把它转化成第二种形式的约束条件构建一个二次函数\(P\left(\sum_im_ix_i-N\right)^2\)。但是如果我们直接使用红线处作为约束条件，通过优化让咖啡的量无限的接近于红线，这有可能导致一种结果是最终咖啡的量会在红线的周围有一个震荡，有可能比红线高一点点。但我们这个约束本身是硬约束，高一点点都不行。那怎么办呢？这里用到的策略是，再准备一个小杯子，我们先把大杯子中的咖啡量优化到接近于红线，然后不管多了少了，再往小杯子里面倒满咖啡。这样的话，可以大概率的保障大杯子中最终剩下的咖啡是低于红线的。这个思路写出来的软约束条件是这样的，我们先定义一堆的slack variable松弛变量（表示额外引入的小咖啡杯）：

\[X'=\{x_{m+1}, x_{m+2}, x_{m+3}, ..., x_{m+p}\} \]

那么可以写出约束条件\(\sum_ic_ix_i\leq U\)的对应函数形式为：

\[P\left(\sum_ic_ix_i+\sum_i^p2^ix_{m+i}-U\right)^2 \]

我们只要尽可能的去优化\(X+X'\)，理想条件下使得这一项约束的结果为0，就可以得到一个符合约束条件的结果。不论\(X'\)的结果如何，\(X\)都是符合约束条件的。类似的思路处理大于号的情况，假如我们要求的是咖啡的量必须高于那一条黄色的线呢？我们再引入一个小杯子，但是这个杯子里面已经装满了咖啡。我们先把大杯的咖啡优化到接近于黄线的量，但此时咖啡的量有可能会比黄线略低，这不符合我们的约束条件。那么我们再把小杯中的咖啡全都倒进大杯子，那么此时大杯子中的咖啡就大概率会是高于黄线的，也就符合我们的约束条件。这里我们需要再定义一些松弛变量：

\[X''=\{x_{m+p+1}, x_{m+p+2}, x_{m+p+3}, ..., x_{m+p+q}\} \]

跟前面类似的方法，可以写出\(\sum_id_ix_i\geq L\)对应的函数形式：

\[P\left(\sum_id_ix_i-\sum_i^q2^ix_{m+p+q}-L\right)^2 \]

这样就可以写出完整的广义0-1规划问题的目标优化函数：

\[Y=P\left(\sum_ic_ix_i+\sum_i^p2^ix_{m+i}-U\right)^2+P\left(\sum_im_ix_i-N\right)^2+P\left(\sum_id_ix_i-\sum_i^q2^ix_{m+p+q}-L\right)^2 \]

根据这个函数，可以去计算QUBO模型的\(Q\)矩阵的相关元素，这里不做展开介绍。完成\(Q\)矩阵元素计算之后，就可以代入求解器或者物理机进行求解。

二次分配问题

Quaratic Assignment二次分配问题，常见于物流建站选址问题。例如下面这个简单示例：

黄色站点的数量跟蓝色地址的数量是一致的，站点和站点之间的流量是固定的，地址和地址之间的距离也是固定的。解决这个问题，就是需要给定一个站点的选址方案，使得总体的运输量（\(流量\times距离\)）最小。如果我们定义站点和地址为：

\[T=\{t_1, t_2, t_3, ..., t_n\}\\ L=\{l_1, l_2, l_3, ..., l_n\} \]

再定义一个二维的流量数组和一个二维的距离数组：

\[f_{00}=0,f_{ij}=f_{ji}=F(t_i,t_j)\\ d_{00}=0,d_{ij}=d_{ji}=D(l_i,l_j) \]

最后，还需要一个布尔数组来标记站点跟地址之间的关系，如果站点\(t_i\)建在\(l_j\)，则令\(x_{ij}=1\)，否则令\(x_{ij}=0\)。那么我们可以计算出目标函数，也就是总运输量为：

\[y=\sum_{i,j,a,b}f_{ij}d_{ab}x_{ia}x_{jb} \]

简单来说就是，当\(t_i,t_j\)两个站点选址在\(l_a,l_b\)时，这两个站点之间的运输量为\(f_{ij}d_{ab}\)，遍历所有的选址，就可以得到总运输量。当然，此时要考虑到两个约束条件：

\[\sum_jx_{ij}=1,\sum_ix_{ij}=1 \]

因为\(x\)是一个\(n\times n\)的矩阵，从矩阵上来看，这个约束条件就是每一行、每一列都有且只有一个元素的值是1。对应到问题场景中就是：每个站点只能建在一个地址上，且每个地址上只能建一个站点。而且考虑到站点数量和地址数量一致，因此每个地址上有且只有一个站点。因为这两个约束条件都是等式，因此约束条件还比较好加：

\[Y=\sum_{i,j,a,b}f_{ij}d_{ab}x_{ia}x_{jb}+P\left(\sum_jx_{ij}-1\right)^2+P\left(\sum_ix_{ij}-1\right)^2 \]

只要优化的足够好，使得所有的惩罚项为0，那么就有\(Y=y\)，最后就可以得到一个符合约束条件的运输量最优解。当然，跟图着色问题有点类似的是，因为这里的\(X\)是一个二维的数组，所以我们需要对它做一个展开：

\[z_f=z_{(i-1)m+j}=x_{ij} \]

在这种变换下就可以计算QUBO模型的\(Q\)矩阵的元素，然后代入求解器或者物理机进行求解。

二次背包问题

前面在广义0-1规划问题中提到过0-1背包问题，在前面这个问题里面我们只注重于物品自身的价值上，而Quadratic Knaspack二次背包问题，除了物品本身的价值之外，还要考虑物品的两两耦合所带来的增值，如下是一个简单的示例：

上面就是一个普通的0-1背包问题，每一个物品都有自己的价值，两两之间互不关联。而下面这个示例，两个熟料瓶和一个瓶盖。如果我们同时装两个熟料瓶，而没有这个盖子，那就凑不出一个完整的瓶子。而如果选择一个塑料瓶和一个瓶盖，那么就得到了一个完整的瓶子，可以放心的用于盛装液体。这两个不同的方案选取，就会带来不同的效果，这就是二次背包问题所要解决的一个问题场景。我们先定义一个布尔数组用于决定是否将物品装进背包：

\[X=\{x_1, x_2, x_3, ..., x_n\},x_i\in\{0,1\} \]

每个物品的重量和价值分别为：

\[M=\{m_1, m_2, m_3, ..., m_n\}\\ V=\{v_1, v_2, v_3, ..., v_n\} \]

上面这些跟0-1背包问题的定义都是一致的，包括约束条件也是一致的：

\[\sum_ix_im_i\leq U \]

装进背包的所有物品的重量，不能超过背包本身的承重能力\(U\)。但是前面提到了，二次背包问题中引入了一个两两耦合的价值增益\(P_{ij}\)，表示\(x_i=1\and x_j=1\)时带来的价值增益。所以二次背包的目标函数形式为：

\[y=\sum_ix_iv_i+\sum_{i,j}P_{ij}x_ix_j \]

回顾一下广义0-1规划问题中的小于号是怎么进行QUBO建模的，我们可以定义一个松弛变量：

\[X'=\{x_{n+1}, x_{n+2}, x_{n+3}, ..., x_{n+q}\},x_i\in\{0,1\} \]

然后给出最终的QUBO模型函数：

\[Y=-\sum_ix_iv_i-\sum_{i,j}P_{ij}x_ix_j+P\left(\sum_{i=1}^nx_im_i+\sum_{i=1}^q2^ix_{n+i}-U\right)^2 \]

把这个式子展开就可以得到QUBO模型的\(Q\)矩阵的元素，然后代入求解器或者物理机进行求解。

总结概要

这篇文章算是对Fred Glover的一篇综述的解读，添加了一些方便直观理解的示例具体的建模过程。对于不同的场景，可以使用不同的惩罚项进行QUBO建模，从而可以使用求解器或者Ising机进行求解。

版权声明

本文首发链接为：https://www.cnblogs.com/dechinphy/p/qubo.html

作者ID：DechinPhy

更多原著文章：https://www.cnblogs.com/dechinphy/

请博主喝咖啡：https://www.cnblogs.com/dechinphy/gallery/image/379634.html

参考文献

A Tutorial on Formulating and Using QUBO Models. Fred Glover, Gary Kochenberger, Yu Du. May 2019