0x0f 前置
其实最小生成树只是某个人用来装*的 ------ 某老师
1x0f 简介
首先给出生成子图的定义(From OI Wiki):

嗯......有点抽象,不妨简化一下:
有一个图 \(G\),如果删去 \(G\) 中的若干条边与若干个点得到一个图 \(G'\),且图 \(G'\) 还保证连通,则称 \(G'\) 为 \(G\) 的生成子图。
那么显然,如果 \(G'\) 是一棵树,那么 \(G'\) 称为 \(G\) 的生成树。
显然,生成树不一定唯一。
那么,最小生成树的"最小"决定于你要求什么,是点权或是边权?由你自己决定。
1x1f 分析
这是一张较为经典的图:
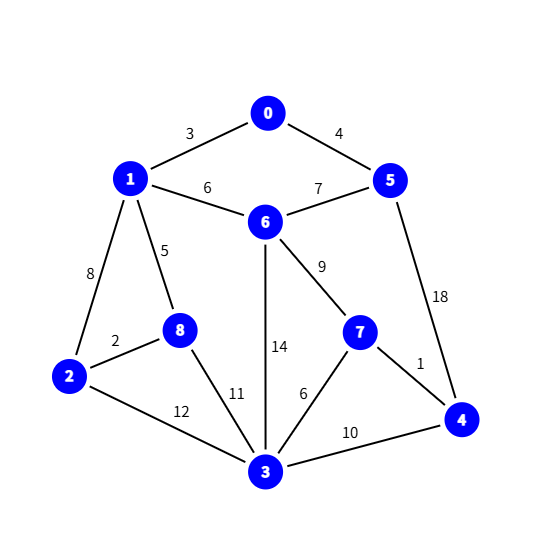
那么这方案求最小生成树:
- 使用 dfs 递归选或不选,再判断是否联通
但是 dfs 递归时间本来就慢,而判连通则需更多的时间复杂度,显然不可行。
但是,我们可以当和珅贪心!
- 按照边权排序
- 选择边7-4,连通7,4
- 选择边2-8,连通2,8
- 选择边1-0,连通1,0
- 选择边0-5,连通0,5
- 选择边1-8,连通1,8
- 选择边1-6,连通1-6
- 选择边3-7,连通3,7
- 选择边6-5,但是由于6,5已经连通,所以可以不加此边
- 选择边1-2,但是由于1,2已经连通,所以可以不加此边
- 选择边6-7,连通6,7
- 已经形成一棵树,后面的边都不选了
那么我们发现,这个方法需要两种操作:
- 判断两个点是否在同一连通块内
- 将两个点添加到同一个连通块内
于是,基于并查集与贪心实现的Kruskal闪亮登场!!!
1x2f 实现
1x2f0fLuogu P3366【模板】最小生成树
首先,定义结构体数组Edge{u,v,w}来表示一条边,使用fa数组来表示并查集
输入及初始化: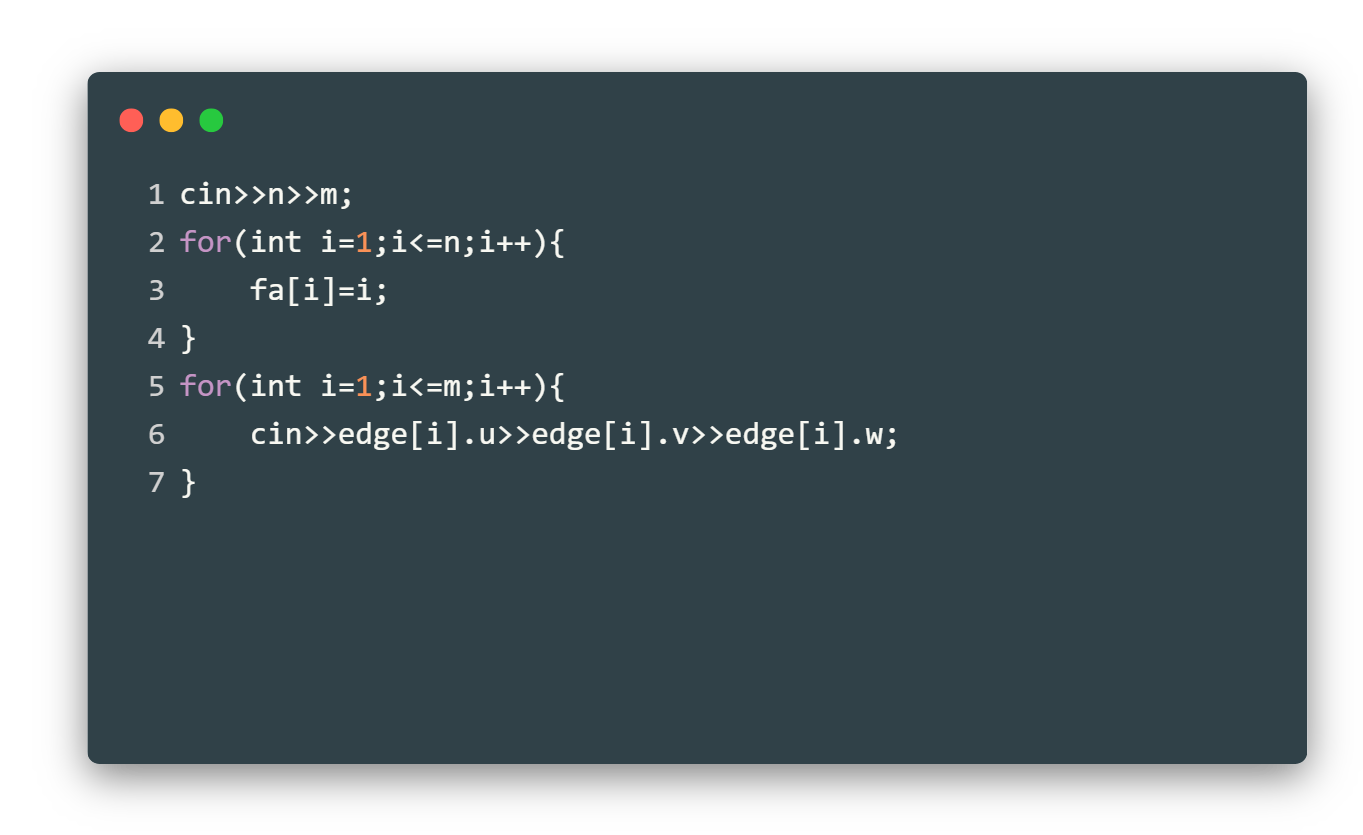
并查集基本操作: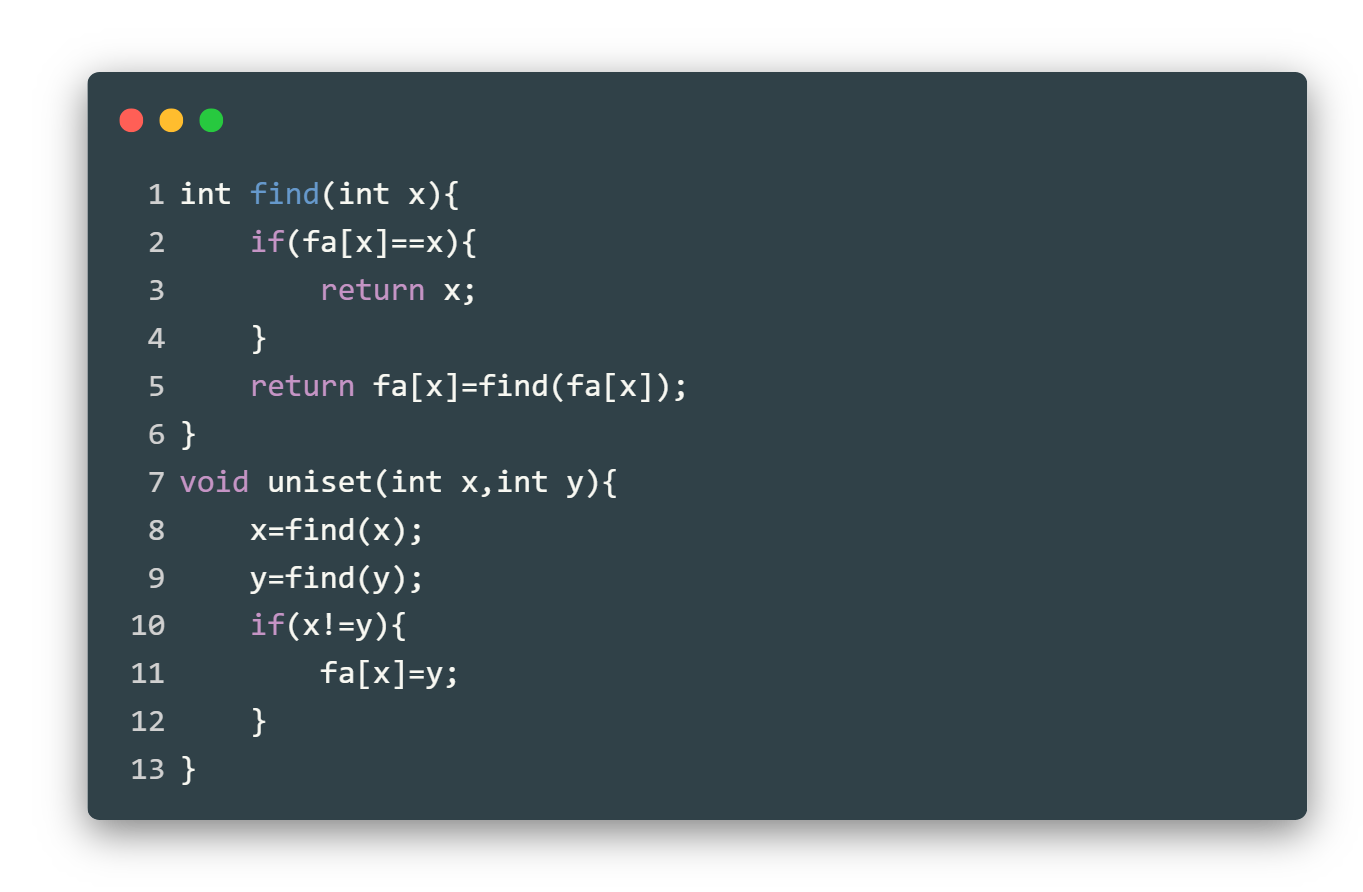
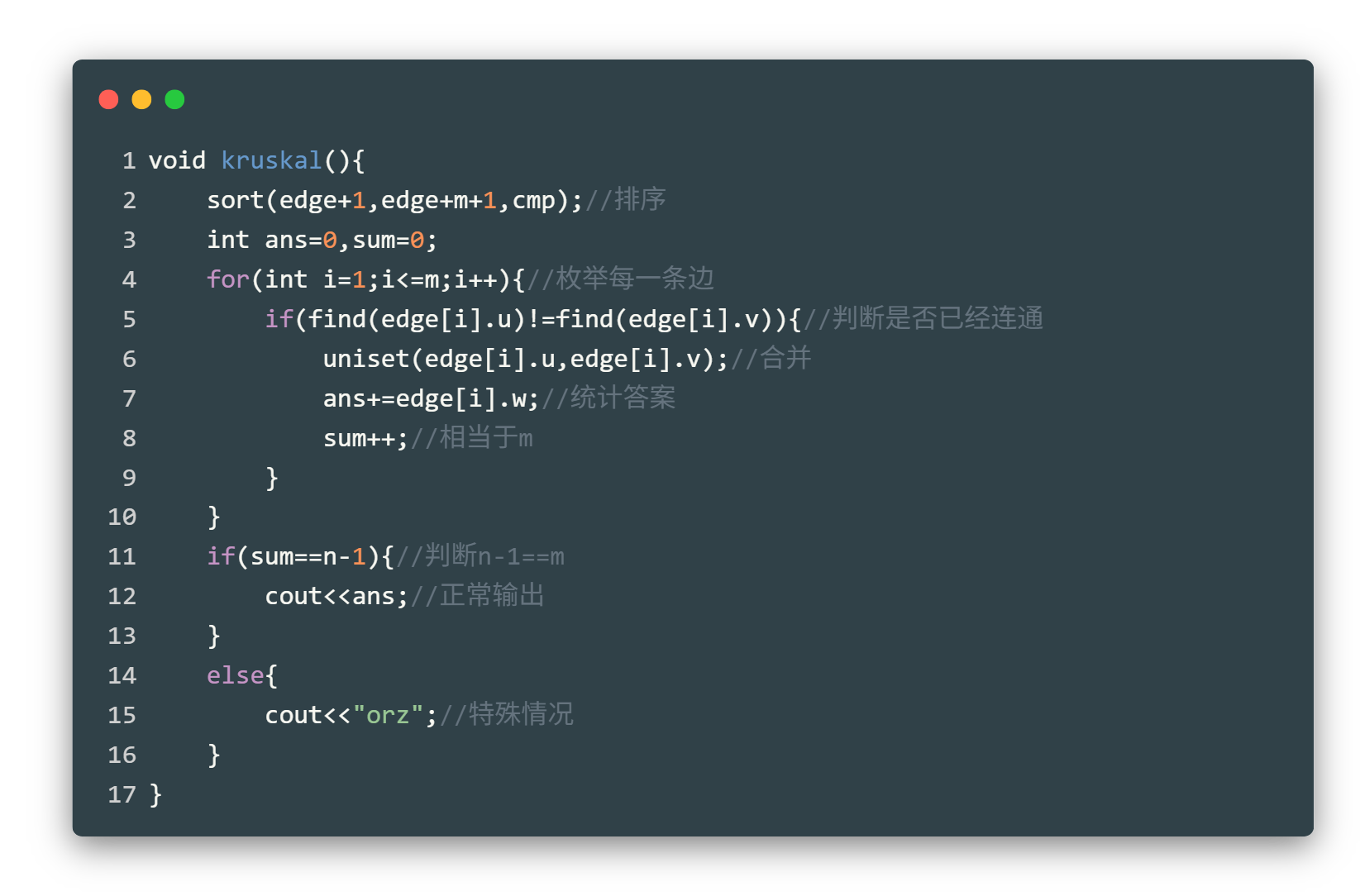
kruskal操作:
特殊处理:
可以发现,在最后如果图本身不连通,还需输出 orz ,我们可以发现,如果图本身不连通,那么最后就不会是一棵树,即 \(n-1\not=m\),判断即可。
1x2f1f Luogu P2820 局域网
读题后可以发现,依旧是求最小生成树,只需在一开始求出边权总和,在最后求差值即可。
主要代码: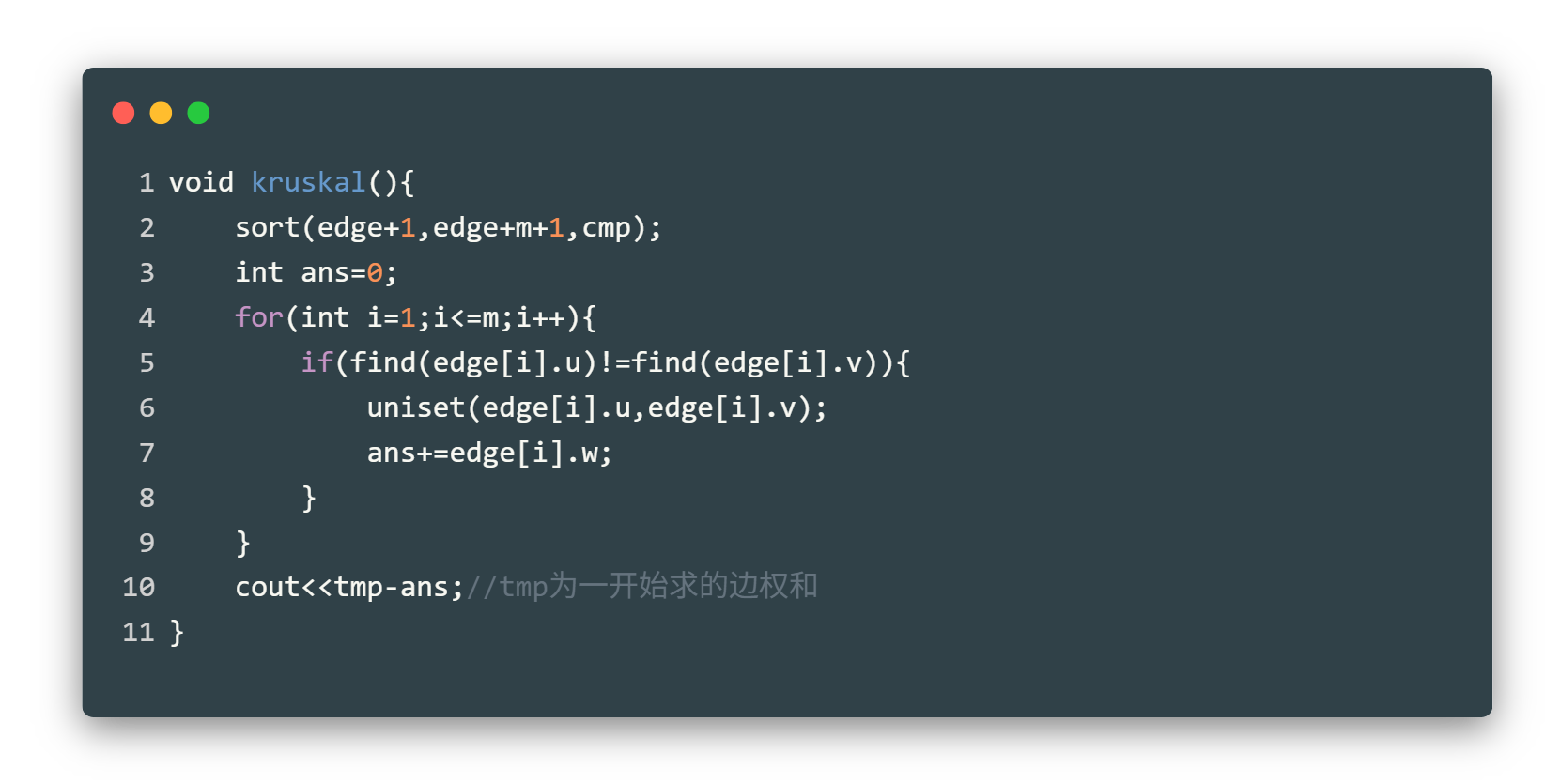
3x0f 练习题
基础题:
附加题: