模拟退火 学习笔记

ShanLing32025-04-27 20:54

模拟退火

前置知识:爬山算法

爬山算法是一种局部择优的方法，采用启发式方法，是对深度优先搜索的一种改进，它利用反馈信息帮助生成解的决策。------Oi Wiki

具体来讲，爬山算法的流程就像一只喝醉了的兔子在山上跳，它每次都会朝它认为更高的地方跳。在跳的过程中，兔子会越来越谨慎（即在水平方向上每次跳的距离比前一次短一些）。

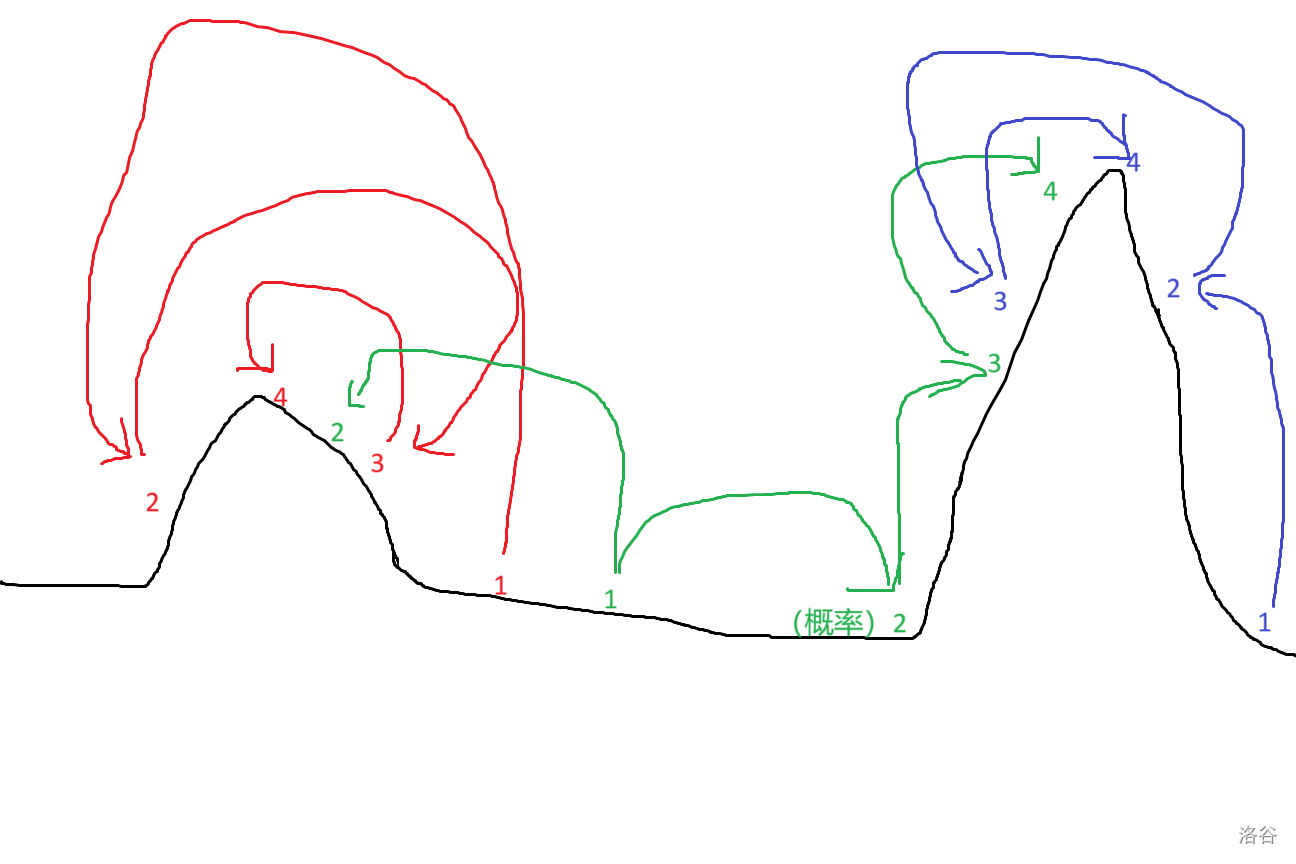
下图中蓝色部分能体现这一过程。注意到在 \(2->3\) 的过程中兔子越过了山顶，但没有关系，随着它跳动距离的减少，它会越来越接近山顶。

例题

[JSOI2008] 球形空间产生器

给出 \(n\) 维空间中，在一 \(n\) 维球体上的 \(n+1\) 个点坐标，求球心坐标。

讲解引用Oi-Wiki上的：

  1. 初始化球心为各个给定点的重心（即其各维坐标均为所有给定点对应维度坐标的平均值），以减少枚举量。

  2. 对于当前的球心，求出每个已知点到这个球心欧氏距离的平均值。

  3. 遍历所有已知点。记录一个改变值 \(cans\)（分开每一维度记录）对于每一个点的欧氏距离，如果大于平均值，就把改变值加上差值，否则减去。实际上并不用判断这个大小问题，只要不考虑绝对值，直接用坐标计算即可。这个过程可以形象地转化成一个新的球心，在空间里推来推去，碰到太远的点就往点的方向拉一点，碰到太近的点就往点的反方向推一点。

  4. 将我们记录的 \(cans\) 乘上温度，更新球心，回到步骤 2

  5. 在温度小于某个给定阈值的时候结束。

    #include <bits/stdc++.h>
    using namespace std;

    int n;
    double spot[15][15],ans[15],dis[15],cans[15];

    void check()
    {
    double sum=0;

    复制代码 
     for(int i=1;i<=n+1;i++)
 {
     dis[i]=cans[i]=0;

     for(int j=1;j<=n;j++)
         dis[i]+=(spot[i][j]-ans[j])*(spot[i][j]-ans[j]);

     dis[i]=sqrt(dis[i]);
     sum+=dis[i];
 }

 sum/=(n+1);

 for(int i=1;i<=n+1;i++)
     for(int j=1;j<=n;j++)
         cans[j]+=(dis[i]-sum)*(spot[i][j]-ans[j])/sum;

    }

    int main( void )
    {
    scanf("%d",&n);
    for(int i=1;i<=n+1;i++)
    for(int j=1;j<=n;j++)
    {
    scanf("%lf",&spot[i][j]);
    ans[j]+=spot[i][j];
    }

    复制代码 
     for(int i=1;i<=n;i++)
     ans[i]/=(n+1);
 
 for(double t=10001;t>=0.0001;t*=0.99995)
 {
     check();
     for(int i=1;i<=n;i++)
         ans[i]+=cans[i]*t;
 }

 for(int i=1;i<=n;i++)
     printf("%.3lf ",ans[i]);

 return 0;

    }

劣势

如上图中红色部分所示，当有多座山时，兔子最终到达的山顶可能不是最高的。

这也就意味着在目标函数不是单峰函数时，爬山算法容易陷入局部最优解。

模拟退火

流程与爬山算法类似，在基础上加入退火操作。

如上图绿色部分所示，兔子有一定概率朝更矮的方向跳，这使它在不是最高的山上也有可能跳到最高的山上。

过程

如果新状态更优就更新状态，否则以一定概率更新。

定义当前温度为 \(T\)，新状态 \(S'\) 与已知状态 \(S\)（新状态由已知状态通过随机的方式得到）之间的能量（值）差为 \(\Delta E\)（\(\Delta E\geqslant 0\)），则不优情况下更新解的概率为 \(e^\frac{-\Delta E}{T}\)。

一些细节

  1. 温度和计算状态的参数对结果影响很大，可以对拍来调参数。
  2. 为保证准确性，可以多执行几次模拟退火。
  3. 即使如此，也可能一次提交无法通过，可以换随机种子多次尝试。

例题一

[HAOI2006] 均分数据

已知 \(n\) 个正整数 \(a_1,a_2 ... a_n\) 。要将它们分成 \(m\) 组，使得各组数据的数值和最平均，即各组数字之和的均方差最小。

对于一种给定的顺序，一个很容易想到的操作方案是将 \(a\) 插进当前和最小的一组。

复制代码 
double ask()
{
    memset(b,0,sizeof(b));
    b[0]=2e9;

    for(int i=1;i<=n;i++)
    {
        int x=0;
        for(int j=1;j<=m;j++)
            if(b[j]<b[x])
                x=j;
        
        b[x]+=a[i];
    }

    double num2=0;
    for(int i=1;i<=m;i++)
        num2+=(num1-b[i])*(num1-b[i]);

    return sqrt(num2/m);
}

其实卡时+每次随机一个排列就可以过了。

每次随机选择两个位置并交换，如果所得的结果更优则更新数组，否则有一定概率更新。

复制代码 
#include <bits/stdc++.h>
using namespace std;
#define urd uniform_real_distribution

int n,m,a[25],b[25];
double num1,ans=2e9;
mt19937 rnd(1919810);

void sa()
{
    for(double st=3000;st>0.00000001;st*=0.95)
    {
        int x=rnd()%n+1,y=rnd()%n+1;
        swap(a[x],a[y]);

        double now=ask();//省略

        if(now<ans)
            ans=now;
        else if(urd<>(0,1)(rnd)>exp(now-ans)/st)
            swap(a[x],a[y]);
    }
}

int main( void )
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        num1+=a[i];
    }

    num1/=m;
    
    const clock_t st=clock();
    while(1)//卡时
    {
        rnd=mt19937(rnd());
        sa();

        const clock_t ed=clock();
        const int time_limit=950;
        if(double(ed-st)*1000/CLOCKS_PER_SEC>=time_limit)
            break;
    }

    printf("%.2lf",ans);

    return 0;
}

例题二

[JSOI2016] 炸弹攻击1

平面上有 \(n\) 个建筑（可视为圆）与 \(m\) 个敌人。你可以在任意位置放置半径不超过 \(R\) 的圆，其范围内不能有任何建筑，求其能包含的最多的敌人数。

该题中答案为整数且范围很小，如果只以答案为状态，函数不平滑，而且有很多位置受建筑影响答案为 \(0\)，这使得函数被分成很多段。

考虑在状态中加入新成分。经过思考可以想到将所有答案为 \(0\) 的位置的状态设为「当前圆为碰到第一个敌人还需增大的半径」，再通过尝试可以找到一个合适的系数。

复制代码 
#include <bits/stdc++.h>
using namespace std;
#define urd uniform_real_distribution

mt19937 rnd(12);

int n,m,mxr,ans;
struct node
{
    int x,y,r;
}a[15],b[1005];

double gtds(double x,double y,double xx,double yy)
{
    return (x-xx)*(x-xx)+(y-yy)*(y-yy);
}

double _count(double x,double y)
{
    int num1=0;
    double num2=1e13,r=mxr;

    for(int i=1;i<=n;i++)
    {
        double dis=sqrt(gtds(a[i].x,a[i].y,x,y));
        r=min(r,max(dis-a[i].r,0.0));
    }

    for(int i=1;i<=m;i++)
    {
        double dis=sqrt(gtds(b[i].x,b[i].y,x,y));
        if(dis<=r)
            num1++;
        num2=min(num2,dis-r);
    }

    ans=max(ans,num1);
    return num1-max(0.0,num2)*14.14;
}

void sa()
{
    double x=0,y=0;
    double ls=_count(x,y);

    for(double st=1e12;st>=1e-8;st*=0.9996)
    {
        double xx=x+urd<>(-10,10)(rnd)*st;
        double yy=y+urd<>(-10,10)(rnd)*st;

        double now=_count(xx,yy);
        if(now>ls || urd<>(0,1)(rnd)<=exp((now-ls)/st))
        {
            x=xx;
            y=yy;
            ls=now;
        }
    }
}

int main( void )
{
    scanf("%d%d%d",&n,&m,&mxr);
    for(int i=1;i<=n;i++)
        scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].r);
    for(int i=1;i<=m;i++)
        scanf("%d%d",&b[i].x,&b[i].y);

    sa();
    rnd=mt19937(20060617);
    sa();
    sa();

    printf("%d",ans);

    return 0;
}

例题三

Coloring

按要求在 \(n \times m\) 的格子上染色，求使得相邻格子颜色不同的数量最少的染色方案。

每次随机交换两个格子的颜色，能使答案更优就保留操作，否则概率保留。

复制代码 
#include <bits/stdc++.h>
using namespace std;
#define urd uniform_real_distribution

mt19937 rnd(chrono::system_clock::now().time_since_epoch().count());

int n,m,c,a[25][25],aa[25][25],ans=2e9,b[25][25],book[25];

int check(int xa,int ya,int xb,int yb)
{
    if(xa<1 || xa>n)
        return 0;
    if(xb<1 || xb>n)
        return 0;
    if(ya<1 || ya>m)
        return 0;
    if(yb<1 || yb>m)
        return 0;
    
    if(a[xa][ya]!=a[xb][yb])
        return 1;
    return 0;
}


void sa()
{
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
                a[i][j]=aa[i][j];
        
    int lst=0;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            lst+=check(i,j,i+1,j)+check(i,j,i,j+1);

    for(double st=1;st>=1e-15;st*=0.99999)
    {
        if(lst<ans)
        {
            ans=lst;
            for(int i=1;i<=n;i++)
                for(int j=1;j<=m;j++)
                    b[i][j]=a[i][j];
        }

        int xa=rnd()%n+1,ya=rnd()%m+1;
        int xb=rnd()%n+1,yb=rnd()%m+1;

        int now=lst;
        now-=check(xa,ya,xa-1,ya)+check(xb,yb,xb-1,yb);
        now-=check(xa,ya,xa+1,ya)+check(xb,yb,xb+1,yb);
        now-=check(xa,ya,xa,ya-1)+check(xb,yb,xb,yb-1);
        now-=check(xa,ya,xa,ya+1)+check(xb,yb,xb,yb+1);

        swap(a[xa][ya],a[xb][yb]);
        now+=check(xa,ya,xa-1,ya)+check(xb,yb,xb-1,yb);
        now+=check(xa,ya,xa+1,ya)+check(xb,yb,xb+1,yb);
        now+=check(xa,ya,xa,ya-1)+check(xb,yb,xb,yb-1);
        now+=check(xa,ya,xa,ya+1)+check(xb,yb,xb,yb+1);
        
        if(now<lst || urd<>(0,1)(rnd)<=exp((lst-now)/st))
            lst=now;
        else
            swap(a[xa][ya],a[xb][yb]);
    }
}

int main( void )
{
    scanf("%d%d%d",&n,&m,&c);
    int nx=1,ny=1;
    for(int i=1;i<=c;i++)
    {
        int x;
        scanf("%d",&x);
        while(x--)
        {
            aa[nx][ny]=i;

            nx++;
            if(nx>n)
            {
                nx=1;
                ny++;
            }
        }
    }

    sa();
    sa();
    sa();

    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
            printf("%d ",b[i][j]);
        putchar('\n');
    }

    return 0;
}
热门推荐
01西电B测-计算机网络综合实验(含验收问题)02KGG转MP3工具|非KGM文件|解密音频03从零安装 LLaMA-Factory 微调 Qwen 大模型成功及所有的坑04YOLOv5改进 | 添加CA注意力机制 + 增加预测层 + 更换损失函数之GIoU05yolov8，yolo11，yolo12 服务器训练到部署全流程 笔记06我决定放弃搞 Java 了07yolov8实战第五天——yolov8+ffmpg实时视频流检测并进行实时推流——（推流，保姆教学）08YOLOv8入门 | 重要性能衡量指标、训练结果评价及分析及影响mAP的因素【发论文关注的指标】09DeepSeek各版本说明与优缺点分析10Coze扣子平台完整体验和实践（附国内和国际版对比）