【深度学习】MLE视角下的VAE与DDPM损失函数推导

正文

最大似然估计的由来

VAE和DDPM都是likelihood-based生成模型，都是通过学习分布->采样实现图像生成的；

这类模型最大的特点就是希望实现

\[\theta = \arg\max \limits_{\theta} \mathbb{E}{x \sim p{data}(x)}[log(p_{\theta}(x))] \]

上述式子是啥意思呢？$\theta$是神经网络的参数集合，$p_{\theta}(x)$是神经网络模型学习（拟合）得到的分布。所以上式意思是我希望我的神经网络生成的图片足够逼真 ，生成出符合原始数据分布的概率足够高。

换一个思路去考虑这个问题，我现在有一个神经网络参数化的$p_{\theta}$，和真实数据分布$p_{data}$

$!NOTE$
这里教个小技巧，看到$p_{\theta}$就当作$N(\mu_{\theta},\sigma_{\theta}^2)$去理解（并不是说所有神经网络都在拟合高斯分布，只是这种情况比较多，且这么理解更加直观。）

我们本质的目的还是说$p_{\theta} \rightarrow p_{data}$，尽可能的逼近

\[\begin{aligned} D_{KL}(p_{data}||p_{\theta}) &= \int p_{data}(x)log\frac{p_{data}(x)}{p_{\theta}(x)}dx \\ &= \int p_{data}(x)logp_{data}(x)dx - \int p_{data}(x)logp_{\theta}(x)dx \\ &=\mathbb{E}{x \sim p{data}(x)}[logp_{data}(x)]-\mathbb{E}{x \sim p{data}(x)}[logp_{\theta}(x)] \end{aligned} \]

又因为$D_{KL}(p_{data}||p_{\theta}) \geq 0$，这就要求$\mathbb{E}{x \sim p{data}(x)}[logp_{\theta}(x)]$尽可能的大，以离散的形式理解：

\[\begin{aligned} \mathbb{E}{x \sim p{data}(x)}[logp_{data}(x)]-\mathbb{E}{x \sim p{data}(x)}[logp_{\theta}(x)] \approx \frac{1}{N}\sum_{i=1}^N logp_{data}(x_i)-\frac{1}{N}\sum_{i=1}^N logp_{\theta}(x_i),x_i \sim p_{data} \end{aligned} \]

当$p_\theta \rightarrow p_{data}$时，那么每次采样得到的$p_{\theta}(x_i)$就是等于$p_{data}(x_i)$，这样就保证$D_{KL}(p_{data}||p_{\theta})$最小。

$!NOTE$
有没有可能$p_{\theta}$和$p_{data}$不相等 ，但是也有样本概率的整体差趋近于0呢？以高斯分布举例$p_{data}(x)=N(175,10^2I),p_{\theta}(x)=N(165,5^2I)$，那么有可能个别甚至一部分 从$p_{data}$采样得到的$x_i$在$p_{\theta}(x_i)$中的概率值会高于 $p_{data}(x_i)$，但是就整体而言，其余部分的均值会拉低这个水平 ，导致最终的$D_{KL}(p_{\theta}||p_{data})$还是会很高。

另一个方面，$D_{KL}(p_{\theta}||p_{data}) \geq 0$，除了两个分布相等之外没有别的可能实现。

那为什么有些资料中，最大似然估计中没有涵盖$\mathbb{E}{x \sim p{data}(x)}$这项呢？

假设有$N$个独立同分布（i.i.d）的样本$\{x_1,x_2,\cdots,x_N\}$，MLE的目标是最大化样本的联合概率

\[\theta=\arg\max \limits_{\theta}=\prod_{i=1}^Np_{\theta}(x_i) \]

直观来说，我希望$p_{\theta}(x)$足够接近于$p_{data}(x)$，这样从$p_{data}(x)$采样得到的$x_i$在$p_{\theta}(x)$分布下的概率值才会尽可能的高。

取对数后转化为求和的形式

\[\theta = \arg \max \limits_{\theta} \sum_{i=1}^Nlogp_{\theta}(x_i) \]

当$N \rightarrow \infty$时，根据大数定律有

\[\frac{1}{N}\sum_{i=1}^Nlogp_{\theta}(x_i) \rightarrow \mathbb{E}{x \sim p{data}(x)}[log(p_{\theta}(x))] \]

因此$\theta = \arg \max \limits_{\theta} \sum_{i=1}^Nlogp_{\theta}(x_i)$和$\theta = \arg\max \limits_{\theta} \mathbb{E}{x \sim p{data}(x)}[log(p_{\theta}(x))]$在形式上取得一致。

VAE的Loss推导

\[\begin{aligned} logp_{\theta}(x)&=logp_{\theta}(x)\int_zq_{\phi}(z|x)dz \\ &=\int_z q_{\phi}(z|x)logp_{\theta}(x)dz \\ &=\mathbb{E}{z \sim q{\phi}(z|x)}[logp_{\theta}(x)] \\ &=\mathbb{E}{z \sim q{\phi}(z|x)}[log\frac{p_{\theta}(x,z)}{p(z|x)}] \\ &=\mathbb{E}{z \sim q{\phi}(z|x)}[log\frac{p_{\theta}(x,z)}{p_{\theta}(z|x)}\frac{q_{\phi}(z|x)}{q_{\phi}(z|x)}] \\ &=\mathbb{E}{z \sim q{\phi}(z|x)}[log\frac{p_{\theta}(x,z)}{q_{\phi}(z|x)}]+\mathbb{E}{z \sim q{\phi}(z|x)}[\frac{q_{\phi}(z|x)}{p_{\theta}(z|x)}] \\ &=\mathbb{E}{z \sim q{\phi}(z|x)}[log\frac{p_{\theta}(x,z)}{q_{\phi}(z|x)}]+D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x))\\ &\geq \mathbb{E}{z \sim q{\phi}(z|x)}[log\frac{p_{\theta}(x,z)}{q_{\phi}(z|x)}] = ELBO \end{aligned} \]

$!NOTE\] MLE、ELBO与Loss之间的联系 1. 对于一些显式的概率模型，直接使用\$\\theta = \\arg \\max \\limits_{\\theta} \\sum_{i=1}\^Nlogp_{\\theta}(x_i)\$公式； 2. 但是对于包含隐变量的概率模型，由于\$p_{\\theta}(x)=\\int p_{\\theta}(x,z)dz\$中对于\$z\$变量的积分过于复杂而**不直接使用MLE的方法进行计算** ；取而代之，是通过构建变分下界（\$ELBO\$）**不等式** 的方式，通过**最大化\$ELBO\$的方式去逼近MLE的目标** 。通过分解单个数据点的\$logp_{\\theta}(x)\$，再扩展到全体数据\$\\sum_{i=1}\^N ELBO_i\$，最终与MLE目标等价，并且通过该不等式**引出最终的损失函数**'； 3. 当目标是**显式函数** 时，Loss是MLE本身；目标是**隐式函数**时，Loss是ELBO（MLE的下界）$

其中，由于$D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x)) \geq 0$，所以把$\mathbb{E}{z \sim q{\phi}(z|x)}[log\frac{p_{\theta}(x,z)}{q_{\phi}(z|x)}]$作为变分下界（ELBO）

\[\begin{aligned} ELBO &= \mathbb{E}{z \sim q{\phi}(z|x)}[log\frac{p_{\theta}(x,z)}{q_{\phi}(z|x)}] \\ &= \mathbb{E}{z \sim q{\phi}(z|x)}[log\frac{p_{\theta}(x|z)p(z)}{q_{\phi}(z|x)}] \\ &=\mathbb{E}{z \sim q{\phi}(z|x)}[logp_{\theta}(x|z)]-\mathbb{E}{z \sim q{\phi}(z|x)}[log\frac{q_{\phi}(z|x)}{p(z)}] \\ &=\mathbb{E}{z \sim q{\phi}(z|x)}[logp_{\theta}(x|z)]-D_{KL}(q_{\phi}(z|x)||p(z)) \end{aligned} \]

在这里我需要更新一下对VAE的认识，之前的文章也是从流程的角度去解释为什么需要一个$q_{\phi}(z|x)$去对后验分布进行拟合，这里我想以MLE推导得出ELBO的角度去进行更深入的解释。

VAE的动态平衡调节

生成图像流程：$x \rightarrow q_{\phi}(z|x) \rightarrow z \rightarrow p_{\theta}(x|z) \rightarrow \hat{x}$

因此根据梯度调优时，VAE的调优策略类似于EM算法

固定$\phi$参数，优化$\theta$参数。在ELBO中$\mathbb{E}{z \sim q{\phi}(z|x)}[logp_{\theta}(x|z)]$表现于提高由解码器生成图像的精确度 。但是此时$\theta$的变动导致与似然分布$p_{\theta}(x|z)$强相关的代理后验分布$p_{\theta}(z|x)$也发生了变化 ，导致$D_{KL}(q_{\phi}(z|x)||p_{\theta}(z|x))$值发生了变化，进而影响了ELBO损失函数的值；
固定$\theta$参数，优化$\phi$参数。因此$q_{\phi}(z|x)$会天然的通过调整$\mu_{\phi}$和$\sigma_{\phi}$去最大化ELBO的数值 ，体现在最小化$D_{KL}(q_{\phi}(z|x)||N(0,I))=\frac{1}{2}(1+log\sigma_{\phi}^2-\mu_{\phi}^2-\sigma_{\phi}^2)$，提高编码器分布与先验分布的近似度 。同时，$\mu_{\phi}$和$\sigma_{\phi}$值的变动生成不同的$z$值采样，又需要让$\theta$参数不断更新进而学习如何精准生图；

二者是一个动态平衡的效果。

$!NOTE\] 如果提高解码器精度所调整的\$\\theta\$导致代理后验分布\$p_{\\theta}(z\|x)\$偏离标准正态分布很远（趋向于一个尖锐的分布，\$z\$集中于一个位置）。那么\$q_{\\phi}(z\|x) \\rightarrow p(z)\$以提高ELBO与\$q_{\\phi}(z\|x) \\rightarrow p_{\\theta}(z\|x)\$以降低\$D_{KL}(q_{\\phi}(z\|x)\|\|p_{\\theta}(z\|x))\$最终提升ELBO不是**背道而驰**的嘛？事实上，由于无法显式计算\$D_{KL}(q_{\\phi}(z\|x)\|\|p_{\\theta}(z\|x))\$，只能通过最大化ELBO，即\$q_{\\phi}(z\|x) \\rightarrow p(z)\$的形式去提升ELBO，这也导致了： 1. 最终的\$q_{\\phi}(z\|x)\$可能与真实的\$p_{\\theta}(z\|x)\$**相隔甚远** ，\$q_{\\phi}(z\|x) \\rightarrow N(0,I)\$是**对抗中妥协** 的结果，试想少了\$D_{KL}(q_{\\phi}(z\|x)\|\|p(z))\$这层约束项，\$p_{\\theta}(z\|x)\$跟着解码器\$\\theta\$参数一变，\$q_{\\phi}(z\|x)\$为了防止\$D_{KL}(q_{\\phi}(z\|x)\|\|p_{\\theta}(z\|x))\$过大影响ELBO的值，真的会跟着走，**导致最终趋向于狄拉克分布，这是我们不想看到的**； 2. 工程实际而言，保证了\$q_{\\phi}(z\|x)\$空间结构趋向于\$N(0,I)\$，这是**精度和多样性的一个妥协**； 3. 个人理解，\$q_{\\phi}(z\|x) \\rightarrow N(0,I)\$也**降低了\$p_{\\theta}(x\|z)\$的学习成本** ，让二者更好的形成一个平衡，最终也会**矫正** 代理后验分布\$p_{\\theta}(z\|x)\$回归标准正态分布；$

MHVAE的Loss推导

Markovian Hierarchical Varitational AutoEncoder，马尔可夫级联VAE

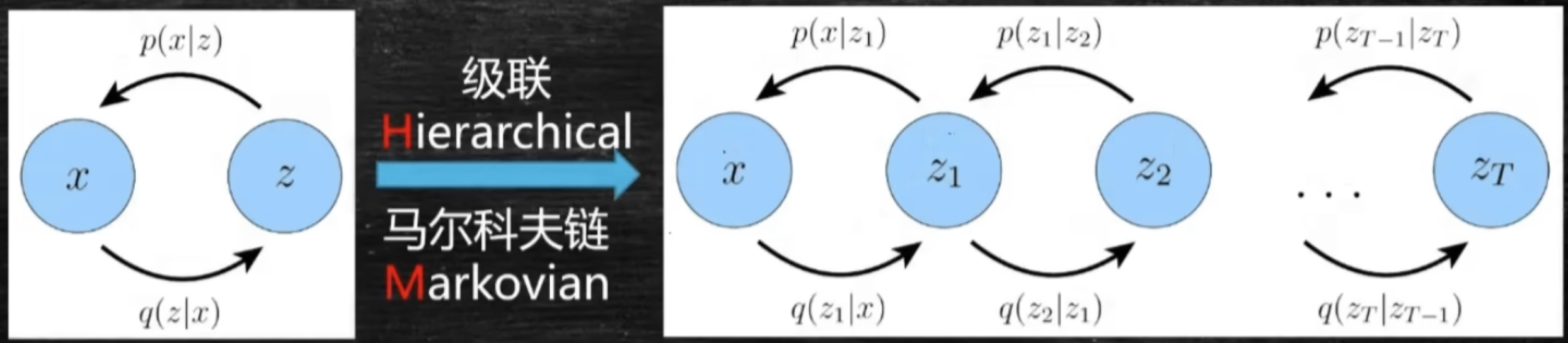
参考之前由MLE推导得到ELBO的公式可知

\[\begin{aligned} logp_{\theta}(x)&=log\int p_{\theta}(x,z_{1:T})dz_{1:T}\\ &=log\int\frac{p_{\theta}(x,z_{1:T})q_{\phi}(z_{1:T}|x)}{q_{\phi}(z_{1:T}|x)}dz_{1:T} \\ &=log\mathbb{E}{q{\phi}(z_{1:T}|x)}[\frac{p_{\theta}(x,z_{1:T})}{q_{\phi}(z_{1:T}|x)}] \\ &\geq\mathbb{E}{q{\phi}(z_{1:T}|x)}[log\frac{p_{\theta}(x,z_{1:T})}{q_{\phi}(z_{1:T}|x)}] = ELBO \\ \end{aligned} \]

$!NOTE$
最后一步用到了琴生不等式，对于一个凸函数而言：$\frac{log(x_1) + log(x_2)}{2} \leq log(\frac{x_1 + x_2}{2})$

DDPM的Loss推导

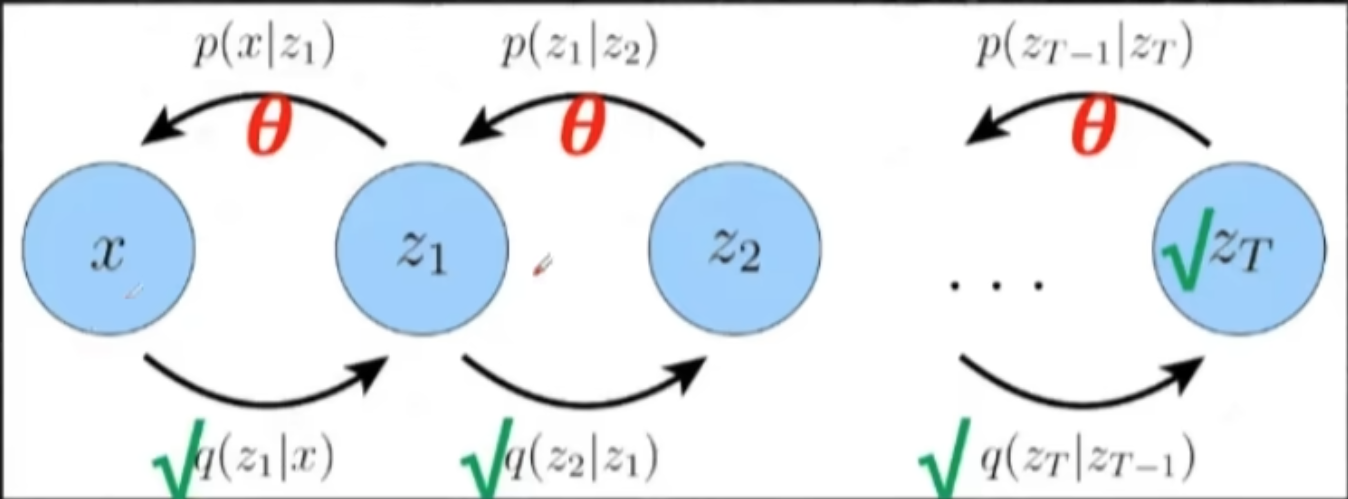
图中是基于MHVAE的标注，替换为$x \rightarrow x_0$、$z_i \rightarrow x_i$

其中加噪过程$q(x_{t}|x_{t-1})$是人为的，具体公式参考[[001 DDPM-v2]]，因此不添加$\phi$参数；

其中去噪过程$p_{\theta}(x_{t-1}|x_t)$是需要学习的，因此添加$\theta$参数进行神经网络参数化操作；

DDPM的ELBO

参考上述MLE推导得到ELBO的公式

\[\begin{aligned} logp_{\theta}(x)&=log\int p_{\theta}(x_{0:T})dx_{1:T}\\ &=log\int\frac{p_{\theta}(x_{0:T})q(x_{1:T}|x_0)}{q(x_{1:T}|x_0)}dx_{1:T} \\ &=log\mathbb{E}{q(x{1:T}|x_0)}[\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}] \\ &\geq\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}] = ELBO \\ \end{aligned} \]

其中

\[\begin{aligned} p_{\theta}(x_{0:T}) &= p(x_T)p(x_{0:T-1}|x_T)\\ &=p(x_T)p(x_{T-1}|x_{T})p(x_{0:T-2}|x_{T-1},x_T)\\ &=p(x_T)p(x_{T-1}|x_{T})p(x_{0:T-2}|x_{T-1}) \\ &=\cdots \\ &=p(x_T)p(x_{T-1}|x_{T})\cdots p(x_0|x_1) \\ &=p(x_T)\prod_{t=1}^Tp(x_{t-1}|x_t) \end{aligned} \]

\[\begin{aligned} q(x_{1:T}|x_0) &= q(x_{2:T}|x_1)q(x_1|x_0) \\ &=q(x_{3:T}|x_2,x_1)q(x_2|x_1)q(x_1|x_0) \\ &=q(x_{3:T}|x_2)q(x_2|x_1)q(x_1|x_0) \\ &=\cdots \\ &=q(x_{T}|x_{T-1})\cdots q(x_2|x_1)q(x_1|x_0)\\ &=\prod_{t=1}^Tq(x_t|x_{t-1}) \end{aligned} \]

代入得

\[\begin{aligned} logp_{\theta}(x)&\geq\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)\prod_{t=1}^Tp_{\theta}(x_{t-1}|x_t)}{\prod_{t=1}^Tq(x_t|x_{t-1})}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)p_{\theta}(x_0|x_1)\prod_{t=2}^Tp_{\theta}(x_{t-1}|x_t)}{\prod_{t=1}^Tq(x_t|x_{t-1})}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)p_{\theta}(x_0|x_1)\prod_{t=1}^{T-1}p_{\theta}(x_{t}|x_{t+1})}{q(x_T|x_{T-1})\prod_{t=1}^{T-1}q(x_t|x_{t-1})}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)p_{\theta}(x_0|x_1)}{q(x_T|x_{T-1})}]+\mathbb{E}{q(x{1:T}|x_0)}[log\prod_{t=1}^{T-1}\frac{p_{\theta}(x_{t}|x_{t+1})}{q(x_t|x_{t-1})}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[logp_{\theta}(x_0|x_1)]+\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})}]+\mathbb{E}{q(x{1:T}|x_0)}[\sum_{t=1}^{T-1}log\frac{p_{\theta}(x_{t}|x_{t+1})}{q(x_t|x_{t-1})}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[logp_{\theta}(x_0|x_1)]+\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})}]+\sum_{t=1}^{T-1}\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_{t}|x_{t+1})}{q(x_t|x_{t-1})}] \\ &=\mathbb{E}{q(x{1}|x_0)}[logp_{\theta}(x_0|x_1)]+\mathbb{E}{q(x{T},x_{T-1}|x_0)}[log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})}]+\sum_{t=1}^{T-1}\mathbb{E}{q(x{t-1},x_t,x_{t+1}|x_0)}[log\frac{p_{\theta}(x_{t}|x_{t+1})}{q(x_t|x_{t-1})}] \\ \end{aligned} \]

$!NOTE$

$\prod_{t=2}^Tp_{\theta}(x_{t-1}|x_t)$可以通过换元法 ，改写成$\prod_{t=1}^{T-1}p_{\theta}(x_{t}|x_{t+1})$；

期望的和等于和的期望；

最后一行由于其它变量都没有用上，因此只保留相关的变量进行采样；

消除变量

\[\begin{aligned} \mathbb{E}{q(x{T},x_{T-1}|x_0)}[log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})}] &= \iint q(x_T,x_{T-1}|x_0)log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})}dx_{T-1}dx_T \\ &=\iint log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})} q(x_T|x_{T-1},x_0)q(x_{T-1}|x_0)dx_{T-1}dx_T \\ &=\iint log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})} q(x_T|x_{T-1})q(x_{T-1}|x_0)dx_{T-1}dx_T \\ &=\int [\int log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})}q(x_T|x_{T-1})dx_T]q(x_{T-1}|x_0)dx_{T-1} \\ &=\int q(x_{T-1}|x_0)[-D_{KL}(q(x_T|x_{T-1})||p_{\theta}(x_T))]dx_{T-1} \\ &=\mathbb{E}{q(x{T-1}|x_0)}[-D_{KL}(q(x_T|x_{T-1})||p_{\theta}(x_T))] \end{aligned} \]

这里尤其尤其要注意的是 ，积分顺序非常关键！

我踩得坑是：

\[\begin{aligned} \mathbb{E}{q(x{T},x_{T-1}|x_0)}[log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})}] &= \iint q(x_T,x_{T-1}|x_0)log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})}dx_{T-1}dx_T \\ &=\iint log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})} q(x_T|x_{T-1},x_0)q(x_{T-1}|x_0)dx_{T-1}dx_T \\ &=\iint log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})} q(x_T|x_{T-1})q(x_{T-1}|x_0)dx_{T-1}dx_T \\ &=\int [\int q(x_{T-1}|x_0)dx_{T-1}]log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})}q(x_T|x_{T-1})dx_T \\ &=\int 1 \times log\frac{p_{\theta}(x_T)}{q(x_T|x_{T-1})}q(x_T|x_{T-1})dx_T \\ &=-D_{KL}(q(x_T|x_{T-1})||p_{\theta}(x_T)) \end{aligned} \]

$!important$

$\int p(x_1|x_2) dx_1=1$，要看清楚这里是积分，$x_1$是变量，积分完之后$x_1$变量就消失了

代入上式，若先把$x_{T-1}$当作变量积分掉的话 ，剩下的带有$x_{T-1}$条件概率的积分就无法完成

因此只能先把$x_T$当作变量积分掉 ，因为剩下的$x_{T-1}$变量没有$x_T$的条件概率。

同理

\[\begin{aligned} \mathbb{E}{q(x{t-1},x_t,x_{t+1}|x_0)}[log\frac{p_{\theta}(x_{t}|x_{t+1})}{q(x_t|x_{t-1})}] &= \iiint q(x_{t-1},x_t,x_{t+1}|x_0)log\frac{p_{\theta}(x_{t}|x_{t+1})}{q(x_t|x_{t-1})}dx_{t-1}dx_t dx_{t+1} \\ &=\iiint q(x_{t+1},x_{t-1}|x_0)q(x_t|x_{t-1})log\frac{p_{\theta}(x_{t}|x_{t+1})}{q(x_t|x_{t-1})}dx_{t-1}dx_t dx_{t+1} \\ &=\iint [\int log\frac{p_{\theta}(x_{t}|x_{t+1})}{q(x_t|x_{t-1})}q(x_t|x_{t-1})dx_t]q(x_{t+1},x_{t-1}|x_0)dx_{t-1}dx_{t+1} \\ &=\iint q(x_{t+1},x_{t-1}|x_0)[-D_{KL}(q(x_t|x_{t-1})||p_{\theta}(x_{t}|x_{t+1}))]dx_{t-1}dx_{t+1} \\ &=\mathbb{E}{q(x{t-1},x_{t+1}|x_0)}[-D_{KL}(q(x_t|x_{t-1})||p_{\theta}(x_{t}|x_{t+1}))] \end{aligned} \]

此时有

\[\begin{aligned} logp_{\theta}(x)&\geq\mathbb{E}{q(x{1}|x_0)}[logp_{\theta}(x_0|x_1)]+\mathbb{E}{q(x{T-1}|x_0)}[-D_{KL}(q(x_T|x_{T-1})||p_{\theta}(x_T))]+\mathbb{E}{q(x{t-1},x_{t+1}|x_0)}[-D_{KL}(q(x_t|x_{t-1})||p_{\theta}(x_{t}|x_{t+1}))] \\ \end{aligned} \]

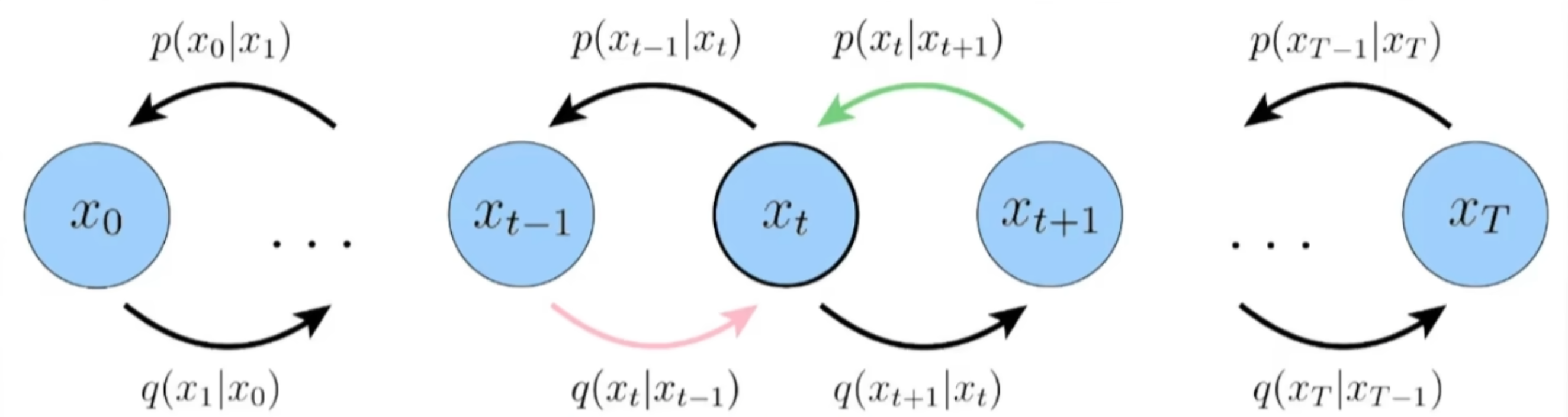
这里出现了一个问题，多元变量求期望方差会很大 ，那么能不能通过一些方法消去部分的变量呢？

马尔可夫性质贝叶斯

\[\begin{aligned} logp_{\theta}(x)&\geq\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)\prod_{t=1}^Tp_{\theta}(x_{t-1}|x_t)}{\prod_{t=1}^Tq(x_t|x_{t-1})}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)p_{\theta}(x_0|x_1)\prod_{t=2}^Tp_{\theta}(x_{t-1}|x_t)}{\prod_{t=1}^Tq(x_t|x_{t-1})}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)p_{\theta}(x_0|x_1)\prod_{t=2}^{T}p_{\theta}(x_{t-1}|x_{t})}{q(x_1|x_0)\prod_{t=2}^{T}q(x_t|x_{t-1})}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)p_{\theta}(x_0|x_1)}{q(x_1|x_{0})}]+\mathbb{E}{q(x{1:T}|x_0)}[log\prod_{t=2}^{T}\frac{p_{\theta}(x_{t-1}|x_{t})}{q(x_t|x_{t-1})}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)p_{\theta}(x_0|x_1)}{q(x_1|x_{0})}]+\mathbb{E}{q(x{1:T}|x_0)}[log\prod_{t=2}^{T}\frac{p_{\theta}(x_{t-1}|x_{t})}{q(x_t|x_{t-1},x_0)}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)p_{\theta}(x_0|x_1)}{q(x_1|x_{0})}]+\mathbb{E}{q(x{1:T}|x_0)}[log\prod_{t=2}^{T}\frac{p_{\theta}(x_{t-1}|x_{t})}{\frac{q(x_{t-1}|x_{t},x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}}] \\ \end{aligned} \]

$!NOTE$

由于马尔可夫性质规定：$x_{t}$时刻只与$x_{t-1}$时刻相关。因此$q(x_t|x_{t-1},x_0)=q(x_t|x_{t-1})$；

但是逆向过程并不满足马尔可夫性质 ，即$q(x_{t-1}|x_{t},x_0) \neq q(x_{t-1}|x_{t})$，因此后文中$q(x_{t-1}|x_{t},x_0)$中的$x_0$一直没有删除；

值得注意的是，我们从原理正向推导出发时，直接在逆向非马尔可夫性质条件下在$p(x_{t}|x_{t-1})$中添加$x_0$条件，并通过预估$\hat{x_0}=f(x_t,t)$的形式来消除新增的$x_0$条件。上面的思路显得比较跳跃且难以想象 ，通过MLE估计ELBO的推导中，在满足马尔科夫性质下利用$q(x_t|x_{t-1})=q(x_t|x_{t-1},x_0)$公式进行推导显得更为合理 ，极度怀疑正向推导加$x_0$的措施是根据ELBO推导过程的trick来的。

其中

\[\begin{aligned} \mathbb{E}{q(x{1:T}|x_0)}[log\prod_{t=2}^{T}{\frac{q(x_{t-1}|x_{t},x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}}] &=\mathbb{E}{q(x{1:T}|x_0)}[log\prod_{t=2}^{T}q(x_{t-1}|x_{t},x_0)]+\mathbb{E}{q(x{1:T}|x_0)}[log\frac{\cancel{q(x_2|x_0)}}{q(x_1|x_0)}+log\frac{\cancel{q(x_3|x_1)}}{\cancel{q(x_2|x_0)}}+\cdots+log\frac{q(x_T|x_0)}{\cancel{q(x_{T-1}|x_0)}}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\prod_{t=2}^{T}q(x_{t-1}|x_{t},x_0)]+\mathbb{E}{q(x{1:T}|x_0)}[log\frac{q(x_T|x_0)}{q(x_{1}|x_0)}] \end{aligned} \]

代入原式得

\[\begin{aligned} logp_{\theta}(x)&\geq\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)p_{\theta}(x_0|x_1)}{q(x_1|x_{0})}]+\mathbb{E}{q(x{1:T}|x_0)}[log\prod_{t=2}^{T}\frac{p_{\theta}(x_{t-1}|x_{t})}{\frac{q(x_{t-1}|x_{t},x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}}] \\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)p_{\theta}(x_0|x_1)}{\cancel{q(x_1|x_{0})}}]+\mathbb{E}{q(x{1:T}|x_0)}[log\prod_{t=2}^{T}\frac{p_{\theta}(x_{t-1}|x_{t})}{q(x_{t-1}|x_{t},x_0)}]+\mathbb{E}{q(x{1:T}|x_0)}[log\frac{\cancel{q(x_1|x_0)}}{q(x_{T}|x_0)}]\\ &=\mathbb{E}{q(x{1:T}|x_0)}[log\frac{p_{\theta}(x_T)p_{\theta}(x_0|x_1)}{q(x_{T}|x_0)}]+\mathbb{E}{q(x{1:T}|x_0)}[\sum_{t=2}^{T}log\frac{p_{\theta}(x_{t-1}|x_{t})}{q(x_{t-1}|x_{t},x_0)}]\\ &=\mathbb{E}{q(x{1}|x_0)}[logp_{\theta}(x_0|x_1)]+\mathbb{E}{q(x{T}|x_0)}[log\frac{p_{\theta}(x_T)}{q(x_{T}|x_0)}]+\mathbb{E}{q(x{t-1},x_t|x_0)}[\sum_{t=2}^{T}log\frac{p_{\theta}(x_{t-1}|x_{t})}{q(x_{t-1}|x_{t},x_0)}] \\ &=\mathbb{E}{q(x{1}|x_0)}[logp_{\theta}(x_0|x_1)]+\mathbb{E}{q(x{T}|x_0)}[log\frac{p_{\theta}(x_T)}{q(x_{T}|x_0)}]+\sum_{t=2}^{T}\mathbb{E}{q(x{t-1},x_t|x_0)}[log\frac{p_{\theta}(x_{t-1}|x_{t})}{q(x_{t-1}|x_{t},x_0)}] \\ &=\mathbb{E}{q(x{1}|x_0)}[logp_{\theta}(x_0|x_1)]-D_{KL}(q(x_{T}|x_0)||p_{\theta}(x_T))+\sum_{t=2}^{T}\mathbb{E}{q(x{t-1},x_t|x_0)}[log\frac{p_{\theta}(x_{t-1}|x_{t})}{q(x_{t-1}|x_{t},x_0)}] \end{aligned} \]

其中

\[\begin{aligned} \mathbb{E}{q(x{t-1},x_t|x_0)}[log\frac{p_{\theta}(x_{t-1}|x_{t})}{q(x_{t-1}|x_{t},x_0)}] &= \iint q(x_{t-1},x_t|x_0)log\frac{p_{\theta}(x_{t-1}|x_{t})}{q(x_{t-1}|x_{t},x_0)}dx_{t-1}dx_t \\ &=\iint q(x_{t-1}|x_{t},x_0)q(x_{t}|x_{0})log\frac{p_{\theta}(x_{t-1}|x_{t})}{q(x_{t-1}|x_{t},x_0)}dx_{t-1}dx_t \\ &=\int [\int log\frac{p_{\theta}(x_{t-1}|x_{t})}{q(x_{t-1}|x_{t},x_0)}q(x_{t-1}|x_{t},x_0)dx_{t-1}]q(x_{t}|x_0)dx_{t} \\ &=\mathbb{E}{q(x{t}|x_0)}[-D_{KL}(q(x_{t-1}|x_{t},x_0)||p_{\theta}(x_{t-1}|x_{t}))] \end{aligned} \]

$!NOTE\] Title 注意上式不能将\$q(x_{t-1},x_t\|x_0)\$分解为\$q(x_t\|x_{t-1})q(x_{t-1}\|x_0)\$，因为不管先对\$x_{t-1}\$还是\$x_t\$积分，都会**在后续被积函数中作为条件存在**$

至此利用马尔可夫性质对完成了多元变量的消除工作：

\[\begin{aligned} logp_{\theta}(x)&\geq\underbrace{\mathbb{E}{q(x{1}|x_0)}[logp_{\theta}(x_0|x_1)]}{重构项}-\underbrace{D{KL}(q(x_{T}|x_0)||p_{\theta}(x_T))}{正则项}+\underbrace{\sum{t=2}^{T}\mathbb{E}{q(x{t}|x_0)}[-D_{KL}(q(x_{t-1}|x_{t},x_0)||p_{\theta}(x_{t-1}|x_{t}))]}_{去噪匹配项} \end{aligned} \]

也可以看到这里前两项与VAE具有相同的形式。

当$T=1$时，即意味着只有一个潜变量$x_1=z$，这时退化到与VAE的ELBO具有完全相同的表达式。

ELBO解析

$\sum_{t=2}^{T}\mathbb{E}{q(x{t}|x_0)}[-D_{KL}(q(x_{t-1}|x_{t},x_0)||p_{\theta}(x_{t-1}|x_{t}))]$是ELBO中占比最大的，优先看这个。

其中$p_{\theta}(x_{t-1}|x_{t})$是模型参数化的结果，$q(x_{t-1}|x_{t},x_0)$是模型需要靠近的对象（ground-truth）。

对[[001 DDPM-v2#后向生成过程|ground-truth的推导]]不再赘述，最终结果为

\[q(x_{t-1}|x_{t},x_0) = N(\frac{1}{\sqrt{\alpha_{t}}}[x_{t}-\frac{\beta_{t}}{\sqrt{\bar{\beta}{t}}}\bar{\epsilon}{t}], \frac{\beta_{t}\bar{\beta}{t-1}}{\bar{\beta}{t}}I) \]

由于最终模型参数化$p_{\theta}(x_{t-1}|x_{t})$是为了接近$q(x_{t-1}|x_{t},x_0)$，那不妨：

直接使用$q(x_{t-1}|x_{t},x_0)$的方差：$\frac{\beta_{t}\bar{\beta}{t-1}}{\bar{\beta}{t}}$；
参考$q(x_{t-1}|x_{t},x_0)$均值的形式去设置预测的变量：$\frac{1}{\sqrt{\alpha_{t}}}[x_{t}-\frac{\beta_{t}}{\sqrt{\bar{\beta}{t}}}\bar{\epsilon}{\theta}]$

代入上述假设，展开$D_{KL}(q(x_{t-1}|x_{t},x_0)||p_{\theta}(x_{t-1}|x_{t}))$

\[\begin{aligned} D_{KL}(q(x_{t-1}|x_{t},x_0)||p_{\theta}(x_{t-1}|x_{t})) &= D_{KL}(N(\frac{1}{\sqrt{\alpha_{t}}}[x_{t}-\frac{\beta_{t}}{\sqrt{\bar{\beta}{t}}}\bar{\epsilon}{t}], \frac{\beta_{t}\bar{\beta}{t-1}}{\bar{\beta}{t}}I)||N(\frac{1}{\sqrt{\alpha_{t}}}[x_{t}-\frac{\beta_{t}}{\sqrt{\bar{\beta}{t}}}\bar{\epsilon}{\theta}], \frac{\beta_{t}\bar{\beta}{t-1}}{\bar{\beta}{t}}I)) \\ \end{aligned} \]

参考

\[D_{KL}(N(\mu_1,\sigma_1^2I)||N(\mu_2,\sigma_2^2))=\log\frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2} \]

得到最终的值为

\[\begin{aligned} D_{KL}(q(x_{t-1}|x_{t},x_0)||p_{\theta}(x_{t-1}|x_{t})) &= \log\frac{\sqrt{\frac{\beta_{t}\bar{\beta}{t-1}}{\bar{\beta}{t}}}}{\sqrt{\frac{\beta_{t}\bar{\beta}{t-1}}{\bar{\beta}{t}}}}+\frac{\frac{\beta_{t}\bar{\beta}{t-1}}{\bar{\beta}{t}}+(\frac{1}{\sqrt{\alpha_{t}}}[x_{t}-\frac{\beta_{t}}{\sqrt{\bar{\beta}{t}}}\bar{\epsilon}{t}]-\frac{1}{\sqrt{\alpha_{t}}}[x_{t}-\frac{\beta_{t}}{\sqrt{\bar{\beta}{t}}}\bar{\epsilon}{\theta}])^2}{2\frac{\beta_{t}\bar{\beta}{t-1}}{\bar{\beta}{t}}}-\frac{1}{2} \\ &=\frac{\beta_t}{2\alpha_t\bar{\beta}{t-1}}\Vert \bar{\epsilon}{\theta}-\bar{\epsilon}_{t} \Vert^2 \end{aligned} \]