最重要:01背包(完全背包)
设dp[i][j]表示前i个物品装进容量为j的背包
分两种情况,要么不要(第一项),要么要(第二项)f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i])
注意,要判断j-w[i]是否为正
完全背包:
f[i][j]=max(f[i-1][j],f[i][j-w[i]]+v[i])
空间优化:
因为上一行用完就不会再用了
每次只会用到上一行的数据
所以只需要保留i-1和i这两行就行
所以考虑滚动数组
原来的数组:
f
| | | | | i=1
| | | | | i=2
| | | | | i=3
......
现在的数组:
f
| | | | | i=1,3,5,...
| | | | | i=2,4,6,...
所以只需要把所有f数组里的"i"变成i%2就行

这种方法很多dp都可以用
那么还有一种方法可以只用一维,但是只有背包能用
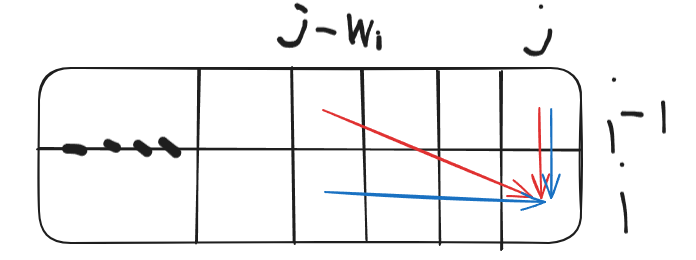
观察到01背包(红)在更新f[i][j]的时候需要f[i-1]的值还未被更新,所以想要大的更新了小的没更新,要逆序枚举
而多重背包(蓝)在更新时需要f[i-1]已经更新,所以要正序枚举
P2979
有两种情况
如果没有大奶酪,那么就是最最最最普通的完全背包
因为我们要尽可能多的奶酪被压扁
先枚举上边的大奶酪是哪一种
再把背包大小变成m*5/4-大奶酪高度
再跑完全背包
but
放上大奶酪也不一定就好
所以你要判断一下,把这种情况和最普通的完全进行比较,选最大的
1941
呵呵,绿题我能会就怪了
这是一道背包题,想不到吧
先假设这是一道简单的dp题
定义f[i][j]表示小鸟在(i,j)位置的最小步数
考虑没有柱子的情况
f[i][j]可以从f[i-1][j+y]或f[i-1][j-x]+1 , f[i-1][j-2x]+2......转移过来
如果你真这么做,那么O(nm^2)直接炸
会发现这些方程有点熟悉
f[i-1][j+y]不就是01背包吗?(-变成+了)
f[i-1][j-x]+1 , f[i-1][j-2x]+2......
不就是f[i][j-w[i]]+v[i]完全背包吗?
所以就是完全背包+01背包
柱子呢?
如果f[i][j]这个位置和柱子重合了
那么直接赋值为inf
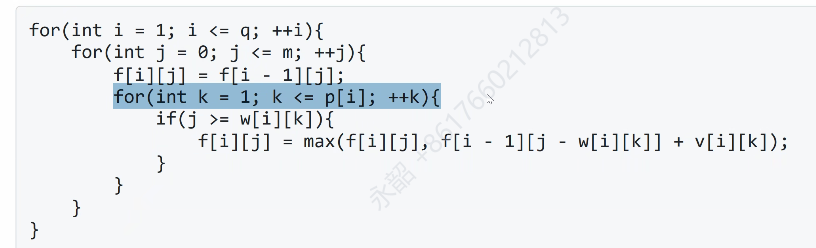
多重背包
如果把每个都拆开成一个一个的小物品做01背包三层循环O(nms[i])太大了
那么二进制优化
会发现对于任何一个正整数n
找到2^(k-1)< n < 2^k
则n可以写成1+2+4+8+...+2^(k-2)+剩下的差
如40=1+2+4+8+16 + 9
那么一个物品就会被拆成log下取整+1个数
这样就优化多了

分组背包
首先是一堆01
给它分个组,每个组里只能选一个
P1782
呵呵,蓝题,呵呵呵呵哈哈哈
前半部分:标准的多重背包,用二进制优化不然就炸
后半部分:分组背包,枚举X
可行性背包

第0列赋值1,O(nm)
但是会发现里面存的都是0,1
所以可以用bitset优化
bool qwq[5]={1,0,1,1,1};
那么bitset也就是10111
bitset<5> qwq=10111
它可以看做一个二进制数,左边是低位,右边是高位
即11101
对其右移1位:1101
那么bitset就变成1011(所以反了)

这是直接用bool数组O(nm)

注意!!标蓝的>>变成<<
会比直接用bool快64(机器字长)倍
P5020
先将a排个序
那么a1一定在新的货币系统中
那么就可以把所有a1的倍数都删掉
再取最小的(假设是a2)
然后再把能用a1和a2都删掉直到没有
令f[i]表示i能否被新货币表示出来
若枚举到ai为0,则这个就是无法被表示的,就新加入货币系统,更新货币系统
P1537
判断:能否凑出一些弹珠为总价值的一半
多重可行性背包
但是直接跑6*2*10^4*2*10^4肯定过不了
你可以二进制优化O(6*log(n[i])*n)
当然,你可以再进行bitset优化,再快64倍O(6*log(n[i])*n/64)


注意!!!状态转移方程是wi和vi打反了,不然也就没啥变化了
f[i][j]的定义很重要!!
AT_abc364_e [ABC364E] Maximum Glutton
f[i][j][k]表示前i个物品,甜度为j,咸度为k,的最大菜肴
发现答案的值域很小,所以考虑把答案和甜/咸换一下
