稀疏贝叶斯谱估计及EM算法求解

稀疏贝叶斯

稀疏贝叶斯学习(sparse bayes learning，SBL)最早被提出是作为一种机器学习算法[1]。但是在这里我们主要用它来做谱估计，作为求解稀疏重构问题的方法[2]。稀疏重构还有个更好听的名字叫压缩感知，但我既不知道他哪里压缩了也不明白他怎么个感知法，也有人说这是两回事，在此咱们不纠结，就叫他稀疏重构了。

稀疏重构问题

对于如下问题：

\[\begin{equation} \boldsymbol{t} = \boldsymbol{\Phi}\boldsymbol{w} + \boldsymbol{\epsilon} \tag{1} \end{equation} \]

其中\(\boldsymbol{\Phi} \in \mathbb{C}^{N\times M}\) 为过完备字典，即\(rank(\boldsymbol{\Phi})=N\ and\ M>N\) 。\(\boldsymbol{t} \in \mathbb{C}^{N \times 1}\) 为观测信号，\(\boldsymbol{w}\in\mathbb{C}^{M \times 1}\)为权重向量，\(\boldsymbol{\epsilon}\in\mathbb{C}^{N\times 1}\)为观测噪声，希望求得\(\boldsymbol{w}\)满足：

\[\begin{equation} \boldsymbol{w} = \arg\min_{\boldsymbol{w}}||\boldsymbol{t} - \boldsymbol{\Phi} \boldsymbol{w}||_2^2 + \lambda||\boldsymbol{w}||_0 \tag{2} \end{equation} \]

其中\(||\boldsymbol{w}||_0\) 为0范数，即\(\boldsymbol{w}\)中非零元的个数。通俗来讲就是用字典矩阵 \(\boldsymbol{\Phi}\) 中最少的向量对\(\boldsymbol{t}\)进行表示，所求的\(\boldsymbol{w}\)就是求得的权重系数。该问题属于\(NP-hard\)问题，无法直接求解，但有许多近似解法，包括LASSO，OMP等，本篇所介绍的SBL也是求解算法之一。

稀疏贝叶斯

式(1)中的噪声 \(\boldsymbol{\epsilon}\) 通常被认为服从0均值高斯分布，即\(\epsilon \sim\mathcal{N}(0,\sigma^2\boldsymbol{I})\)，则\(\boldsymbol{t}\)的条件概率密度函数可以写作:

\[\begin{equation} p(\boldsymbol{t}|\boldsymbol{w};\sigma^2)=(2\pi\sigma^2)^{-\frac{N}{2}}\exp(-\frac{1}{2\sigma^2} ||\boldsymbol{t} - \boldsymbol{\Phi} \boldsymbol{w}||_2^2) \tag{3} \end{equation} \]

同时假定\(\boldsymbol{w}\)的先验服从高斯分布：

\[\begin{equation} p(\boldsymbol{w};\boldsymbol{\Gamma})=(2\pi)^{-\frac{M}{2}}|\boldsymbol{\Gamma}|^{-\frac{1}{2}}\exp(-\frac{1}{2}\boldsymbol{w}^H{\boldsymbol{\Gamma}^{-1}\boldsymbol{w}}) \tag{4} \end{equation} \]

其中\(\boldsymbol{\Gamma}=diag([\gamma_1,\gamma_2,...,\gamma_M]^T)\)为对角阵，是权重的方差。这里通过式(3)和式(4)可以求得边际概率：

\[\begin{align} p(\boldsymbol{t};\boldsymbol{\Gamma},\boldsymbol{\sigma^2})=&\int p(\boldsymbol{t}|\boldsymbol{w};\sigma^2)p(\boldsymbol{w};\boldsymbol{\Gamma})d\boldsymbol{w}\nonumber \\ =&\int(2\pi\sigma^2)^{-\frac{N}{2}}(2\pi)^{-\frac{M}{2}}|\boldsymbol{\Gamma}|^{-\frac{1}{2}}\exp(-\frac{1}{2\sigma^2} ||\boldsymbol{t} - \boldsymbol{\Phi} \boldsymbol{w}||_2^2-\frac{1}{2}\boldsymbol{w}^H{\boldsymbol{\Gamma}^{-1}\boldsymbol{w}})d\boldsymbol{w} \tag{5} \end{align} \]

对于上式，先重点看指数里面部分：

\[\begin{align} &-\frac{1}{2\sigma^2} ||\boldsymbol{t} - \boldsymbol{\Phi} \boldsymbol{w}||_2^2-\frac{1}{2}\boldsymbol{w}^H{\boldsymbol{\Gamma}^{-1}\boldsymbol{w}}\nonumber \\ = &-\frac{1}{2}[\sigma^{-2}\boldsymbol{t}^H\boldsymbol{t}-2\sigma^{-2}\boldsymbol{t}^H\boldsymbol{\Phi} \boldsymbol{w}+\boldsymbol{w}^H(\sigma^{-2}\boldsymbol{\Phi}^H\boldsymbol{\Phi}+\boldsymbol{\Gamma}^{-1})\boldsymbol{w}]\nonumber\\ =&-\frac{1}{2}[\sigma^{-2}\boldsymbol{t}^H\boldsymbol{t}-2\sigma^{-2}\boldsymbol{t}^H\boldsymbol{\Phi} \boldsymbol{w}+\boldsymbol{w}^H\boldsymbol{\Sigma_w}^{-1}\boldsymbol{w}]\nonumber \\ =&-\frac{1}{2}(\sigma^{-2}\boldsymbol{\Sigma_w\Phi}^H\boldsymbol{t}-\boldsymbol{w})^H\boldsymbol{\Sigma_w}^{-1}(\sigma^{-2}\boldsymbol{\Sigma_w\Phi}^H\boldsymbol{t}-\boldsymbol{w})-\frac{1}{2}[\boldsymbol{t}^H(\boldsymbol{I-\boldsymbol{\Phi}\boldsymbol{\Sigma_w}\boldsymbol{\Phi}^H})\boldsymbol{t}] \tag{6} \end{align} \]

其中\(\boldsymbol{\Sigma_w}=(\sigma^{-2}\boldsymbol{\Phi}^H\boldsymbol{\Phi}+\boldsymbol{\Gamma}^{-1})^{-1}\)，并令\((\boldsymbol{I-\boldsymbol{\Phi}\boldsymbol{\Sigma_w}\boldsymbol{\Phi}^H})^{-1} = \boldsymbol{\Sigma_t}\)，根据矩阵求逆引理可以推导出\(\boldsymbol{\Sigma_t} = \sigma^2\boldsymbol{I}+\boldsymbol{\Phi\Gamma\Phi}^H\)。

然后将上述结果带入(5):

\[\begin{align} &p(\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)\nonumber \\=&(2\pi\sigma^2)^{-\frac{N}{2}}(2\pi)^{-\frac{M}{2}}|\boldsymbol{\Gamma}|^{-\frac{1}{2}}\exp(-\frac{1}{2}\boldsymbol{t}^H\boldsymbol{\Sigma_t}^{-1}\boldsymbol{t})\nonumber \\ &\ \ \int\exp[-\frac{1}{2}(\sigma^{-2}\boldsymbol{\Sigma_w\Phi}^H\boldsymbol{t}-\boldsymbol{w})^H\boldsymbol{\Sigma_w}^{-1}(\sigma^{-2}\boldsymbol{\Sigma_w\Phi}^H\boldsymbol{t}-\boldsymbol{w})]d\boldsymbol{w} \tag{7} \end{align} \]

可以看出指数上凑出了高斯分布的形式，但还差指数外的系数。要凑成完整的高斯分布，注意到\(\sigma^{-\frac{N}{2}}|\boldsymbol{\Sigma_w}|^{\frac{1}{2}}|\boldsymbol{\Gamma}|^{-\frac{1}{2}} = |\boldsymbol{\Sigma_t}|^{-\frac{1}{2}}\)，可得：

\[\begin{align} &p(\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)\nonumber \\ =&(2\pi)^{-\frac{N}{2}}|\boldsymbol{\Sigma_t}|^{-\frac{1}{2}}\exp(-\frac{1}{2}\boldsymbol{t}^H\boldsymbol{\Sigma_t}^{-1}\boldsymbol{t})\nonumber \\ &\ \ \int(2\pi)^{-\frac{M}{2}}|\boldsymbol{\Sigma_w}|^{-\frac{1}{2}}\exp[-\frac{1}{2}(\sigma^{-2}\boldsymbol{\Sigma_w\Phi}^H\boldsymbol{t}-\boldsymbol{w})^H\boldsymbol{\Sigma_w}^{-1}(\sigma^{-2}\boldsymbol{\Sigma_w\Phi}^H\boldsymbol{t}-\boldsymbol{w})]d\boldsymbol{w} \tag{8} \end{align} \]

积分内积完结果为\(1\)，所以：

\[\begin{align} &p(\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)=(2\pi)^{-\frac{N}{2}}|\boldsymbol{\Sigma_t}|^{-\frac{1}{2}}\exp(-\frac{1}{2}\boldsymbol{t}^H\boldsymbol{\Sigma_t}^{-1}\boldsymbol{t}) \tag{9} \end{align} \]

另外，积分内积掉的为\(\boldsymbol{w}\)的后验分布：

\[\begin{align} &p(\boldsymbol{w}|\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)\nonumber\\ =&(2\pi)^{-\frac{M}{2}}|\boldsymbol{\Sigma_w}|^{-\frac{1}{2}}\exp[-\frac{1}{2}(\sigma^{-2}\boldsymbol{\Sigma_w\Phi}^H\boldsymbol{t}-\boldsymbol{w})^H\boldsymbol{\Sigma_w}^{-1}(\sigma^{-2}\boldsymbol{\Sigma_w\Phi}^H\boldsymbol{t}-\boldsymbol{w})]\nonumber\\ =&\mathcal{N}(\boldsymbol{\mu_w},\boldsymbol{\Sigma_w}) \tag{10} \end{align} \]

其中\(\boldsymbol{\mu_w} = \sigma^{-2}\boldsymbol{\Sigma_w\Phi}^H\boldsymbol{t}\)，\(\boldsymbol{\Sigma_w}=(\sigma^{-2}\boldsymbol{\Phi}^H\boldsymbol{\Phi}+\boldsymbol{\Gamma}^{-1})^{-1}\)。我们可以选择\(\boldsymbol{\mu}\)作为\(\boldsymbol{w}\)的求解结果（均值嘛，合情合理），但是算\(\boldsymbol{\mu}\)就要知道\(\sigma^2\)和\(\boldsymbol{\Gamma}\)，这俩可以通过对\(p(\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)\)进行最大似然估计求得，但是很不幸，直接求解似然函数是求不出来的（你可以试试，我没算出来，当然参考文献里也没算出来），而且这大概率不是个凸函数，最优解也算不出来，算个次优解意思意思得了。下面介绍下用EM算法求解这个问题。

EM算法

EM算法是怎么回事，什么思想，什么原理网上其他帖子已经讲的很好了[3]，这里直接介绍如何求解上述问题。

理论推导

我们的的核心问题还是要对\(p(\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)\)最大似然求解参数，即：

\[\begin{align} \sigma^2,\boldsymbol{\Gamma} =& \arg\max_{\sigma^2,\boldsymbol{\Gamma}}\mathcal{L}{(\sigma^2,\boldsymbol{\Gamma})}\nonumber\\ \mathcal{L}{(\sigma^2,\boldsymbol{\Gamma})} &= \log[p(\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)] \tag{11} \end{align} \]

然后引入\(\boldsymbol{w}\)，将似然函数写作：

\[\begin{align} \log[p(\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)]&= \log[\int p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)d\boldsymbol{w}] \nonumber\\ =&\log[\int \frac{Q(\boldsymbol{w})}{Q(\boldsymbol{w})}p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)d\boldsymbol{w}] \tag{12} \end{align} \]

上式中\(Q(\boldsymbol{w})\)是\(\boldsymbol{w}\)的一个函数，显然它可以是任意值不为零的函数，此时我们认为它是\(\boldsymbol{w}\)的某个分布函数，因此上式的积分可以写作期望形式：

\[\begin{align} \log[p(\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)] =&\log[\mathbf{E}_{\boldsymbol{w}\sim Q(\boldsymbol{w})} \frac{p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)}{Q(\boldsymbol{w})}] \tag{13} \end{align} \]

对上式进一步操作需要用到Jensen不等式，Jensen不等式网上有详细讲解[4]，大概就是对于一个随机变量\(X\) 和一个函数\(f(X)\) ，当\(f\)的二阶导小于0（上凸）时\(f(\mathbf{E}(X)) \geq \mathbf{E}f(X)\)，等号成立的条件是\(X = \mathbf{E}(X)\)。则式(13)可写为：

\[\begin{align} \log[p(\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)] =&\log[\mathbf{E}{\boldsymbol{w}\sim Q(\boldsymbol{w})} \frac{p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)}{Q(\boldsymbol{w})}]\nonumber\\ \geq & \mathbf{E}{\boldsymbol{w}\sim Q(\boldsymbol{w})} \log[p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)]-\mathbf{E}_{\boldsymbol{w}\sim Q(\boldsymbol{w})}\log[Q(\boldsymbol{w})]\nonumber\\ =& \mathcal{J}(\sigma^2,\boldsymbol{\Gamma}) \tag{14} \end{align} \]

这里我们得到了\(\mathcal{L}{(\sigma^2,\boldsymbol{\Gamma})}\)的一个下界\(\mathcal{J}(\sigma^2,\boldsymbol{\Gamma})\)，理论上可以通过最大化\(\mathcal{J}(\sigma^2,\boldsymbol{\Gamma})\)来最大化\(\mathcal{L}{(\sigma^2,\boldsymbol{\Gamma})}\)，但是一眼望去\(\mathcal{J}(\sigma^2,\boldsymbol{\Gamma})\)更布嚎算，至少\(Q(\boldsymbol{w})\)是啥咱还不知道呢！所以得确定下\(Q(\boldsymbol{w})\)。

首先可以确定的是，在固定\(\sigma^2\)和\(\boldsymbol{\Gamma}\)时，根据Jensen不等式取得等号的条件，\(\mathcal{J}(\sigma^2,\boldsymbol{\Gamma})\)能取到的最大值就是\(\mathcal{L}{(\sigma^2,\boldsymbol{\Gamma})}\)，取得最大值的条件是期望内的数是个常数（与所求期望的随机变量无关）即\(\frac{p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)}{Q(\boldsymbol{w})}\)与\(\boldsymbol{w}\)无关。不难看出，满足此条件的\(Q(\boldsymbol{w})\)为：

\[\begin{align} Q(\boldsymbol{w}) = p(\boldsymbol{w}|\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2) \tag{15} \end{align} \]

但是这样直接把\(Q(\boldsymbol{w})\)代回\(\mathcal{J}(\sigma^2,\boldsymbol{\Gamma})\)让他等于\(\mathcal{L}{(\sigma^2,\boldsymbol{\Gamma})}\)那不是就又绕回去了，所以不能这么干。聪明的人们想到了两步走的方法：

第一步，用当前现有的\(\sigma^2_{(k)}\)和\(\boldsymbol{\Gamma}{(k)}\)，得到\(Q{(k)}(\boldsymbol{w}) = p(\boldsymbol{w}|\boldsymbol{t};\boldsymbol{\Gamma}{(k)},\sigma^2{(k)})\)，并用\(Q_{(k)}(\boldsymbol{w})\)计算出\(\mathcal{J}{(k)}(\sigma^2,\boldsymbol{\Gamma})=\mathbf{E}{\boldsymbol{w}\sim Q_{(k)}(\boldsymbol{w})} \log[p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)]-\mathbf{E}{\boldsymbol{w}\sim Q{(k)}(\boldsymbol{w})}\log[Q_{(k)}(\boldsymbol{w})]\) ，这就是EM算法中的E步，这一步是从Jensen不等式的层面对\(\mathcal{J}(\sigma^2,\boldsymbol{\Gamma})\)进行最大化，使\(\mathcal{J}_{(k)}(\sigma^2,\boldsymbol{\Gamma})\)逼近\(\mathcal{L}{(\sigma^2,\boldsymbol{\Gamma})}\)。

第二步，固定\(Q_{(k)}(\boldsymbol{w})\)不动，通过最大化\(\mathcal{J}{(k)}(\sigma^2,\boldsymbol{\Gamma})\)求\(\sigma^2{(k+1)}\)和\(\boldsymbol{\Gamma}{(k+1)}\)。由于固定\(Q{(k)}(\boldsymbol{w})\)以后\(\mathcal{J}{(k)}(\sigma^2,\boldsymbol{\Gamma})\)中的\(\mathbf{E}{\boldsymbol{w}\sim Q_{(k)}(\boldsymbol{w})}\log[Q_{(k)}(\boldsymbol{w})]\)始终为常数，所以在第一步其实就用不到，直接丢掉。于是乎有：

\[\begin{align} \sigma^2_{(k+1)},\boldsymbol{\Gamma}{(k+1)} =& \arg\max{\sigma^2,\boldsymbol{\Gamma}}\mathbf{E}{\boldsymbol{w}\sim Q{(k)}(\boldsymbol{w})} \log[p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)] \tag{16} \end{align} \]

这就是EM算法中的M步，这一步是对逼近\(\mathcal{L}{(\sigma^2,\boldsymbol{\Gamma})}\)的\(\mathcal{J}{(k)}(\sigma^2,\boldsymbol{\Gamma})\)最大化，让得到的\(\sigma^2{(k+1)},\boldsymbol{\Gamma}{(k+1)}\)进一步趋近最优解。把M步中算出的\(\sigma^2{(k+1)},\boldsymbol{\Gamma}_{(k+1)}\)再拿回E步，就完成了一次迭代。

目前为止还是理论层面，我们得回到我们的问题，看看\(\mathbf{E}{\boldsymbol{w}\sim Q{(k)}(\boldsymbol{w})} \log[p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)]\)以及\(\sigma^2_{(k+1)},\boldsymbol{\Gamma}_{(k+1)}\)到底怎么算。

EM算法求解SBL

先看\(\mathbf{E}{\boldsymbol{w}\sim Q{(k)}(\boldsymbol{w})} \log[p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)]\)，其中:

\[p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)=p(\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)p(\boldsymbol{w}|\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2) =p(\boldsymbol{t}|\boldsymbol{w};\sigma^2)p(\boldsymbol{w};\boldsymbol{\Gamma}) \tag{17} \]

\(p(\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)\)在式(7)，\(p(\boldsymbol{w}|\boldsymbol{t};\boldsymbol{\Gamma},\sigma^2)\)在式(10)，\(p(\boldsymbol{t}|\boldsymbol{w};\sigma^2)\)在式(3)，\(p(\boldsymbol{w};\boldsymbol{\Gamma})\)在式(4)，随便选一对就能算出\(p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)\)，我这里就不算了。

对计算的结果取对数后得到：

\[\begin{align} &\log[p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)] \nonumber\\ =&-\frac{N}{2}log(\sigma^2)-\frac{1}{2}log|\Gamma|-\frac{1}{2\sigma^2}(\boldsymbol{t}^H\boldsymbol{t}+2\boldsymbol{t}^H\boldsymbol{\Phi w}+\boldsymbol{w}^H\boldsymbol{\Phi}^H\boldsymbol{\Phi}\boldsymbol{w})-\frac{1}{2}\boldsymbol{w}^H\boldsymbol{\Gamma}^{-1}\boldsymbol{w}+C \tag{18} \end{align} \]

然后求期望，为了避免式子冗长，后面把没用的常数\(C\)扔了，并将\(\mathbf{E}{\boldsymbol{w}\sim Q{(k)}(\boldsymbol{w})}\)简写为\(\mathbf{E}_{(k)}\)：

\[\begin{align} &\mathbf{E}{(k)}\log[p(\boldsymbol{t},\boldsymbol{w};\boldsymbol{\Gamma},\sigma^2)] \nonumber\\ =&-\frac{N}{2}log(\sigma^2)-\frac{1}{2}log|\Gamma|\nonumber\\ &-\frac{1}{2\sigma^2}(\boldsymbol{t}^H\boldsymbol{t}+2\mathbf{E}{(k)}[\boldsymbol{t}^H\boldsymbol{\Phi} {w}]+\mathbf{E}{(k)}[\boldsymbol{w}^H\boldsymbol{\Phi}^H\boldsymbol{\Phi}\boldsymbol{w}])-\frac{1}{2}\mathbf{E}{(k)}[\boldsymbol{w}^H\boldsymbol{\Gamma}^{-1}\boldsymbol{w}]\nonumber\\ =&\mathcal{J}_{(k)}(\sigma^2,\boldsymbol{\Gamma}) \tag{19} \end{align} \]

由于此刻\(\boldsymbol{w}\sim Q_{(k)}(\boldsymbol{w}),Q_{(k)}(\boldsymbol{w}) = p(\boldsymbol{w}|\boldsymbol{t};\boldsymbol{\Gamma}{(k)},\sigma^2{(k)})\)，并结合式(10)，可得出\(\mathbf{E}{(k)}[\boldsymbol{t}^H\boldsymbol{\Phi} {w}]=\boldsymbol{t}^H\boldsymbol{\Phi}{\mu}{(k)}\)，\(\mathbf{E}{(k)}[\boldsymbol{w}^H\boldsymbol{\Phi}^H\boldsymbol{\Phi}\boldsymbol{w}]=tr[\boldsymbol{\Phi}^H\boldsymbol{\Phi\Sigma_w}^{(k)}]+\boldsymbol{\mu}{(k)}^H\boldsymbol{\Phi}^H\boldsymbol{\Phi}\boldsymbol{\mu}{(k)}\)，\(\mathbf{E}{(k)}[\boldsymbol{w}^H\boldsymbol{\Gamma}^{-1}\boldsymbol{w}] = tr[\boldsymbol{\Gamma}^{-1}{(k)}\boldsymbol{\Sigma_w^{(k)}}]+\boldsymbol{\mu}{(k)}^H\boldsymbol{\Gamma}^{-1}\boldsymbol{\mu}{(k)}\)，其中\(\boldsymbol{\Sigma_w}^{(k)}=(\sigma{(k)}^{-2}\boldsymbol{\Phi}^H\boldsymbol{\Phi}+\boldsymbol{\Gamma}{(k)}^{-1})^{-1}\)，\(\boldsymbol{\mu}{(k)}= \sigma_{(k)}^{-2}\boldsymbol{\Sigma_w^{(k)}}\boldsymbol{\Phi}^H\boldsymbol{t}\)，\(tr(\cdot)\)为求矩阵的迹，即主对角线元素的和。对于二次型求期望可以参考matrix cookbook[5]。然后有：

\[\begin{align} &\mathcal{J}{(k)}(\sigma^2,\boldsymbol{\Gamma})\nonumber\\ =&-\frac{N}{2}log(\sigma^2)-\frac{1}{2}log|\Gamma|\nonumber\\ &-\frac{1}{2\sigma^2} (\boldsymbol{t}^H\boldsymbol{t} +\boldsymbol{t}^H\boldsymbol{\Phi}{\mu}{(k)} +tr[\boldsymbol{\Phi}^H\boldsymbol{\Phi\Sigma_w}^{(k)}]+\boldsymbol{\mu}{(k)}^H\boldsymbol{\Phi}^H\boldsymbol{\Phi}\boldsymbol{\mu}{(k)})\nonumber\\ &-\frac{1}{2}(tr[\boldsymbol{\Gamma}^{-1}{(k)}\boldsymbol{\Sigma_w^{(k)}}]+\boldsymbol{\mu}{(k)}^H\boldsymbol{\Gamma}^{-1}\boldsymbol{\mu}_{(k)}) \tag{20} \end{align} \]

上述部分算是EM算法中的E步，下面看M步，即最大化\(\mathcal{J}{(k)}(\sigma^2,\boldsymbol{\Gamma})\)来求\(\sigma^2{(k+1)}\)和\(\boldsymbol{\Gamma}_{(k+1)}\)。最大化的方式就是求导，导函数为0的点即为最大值。当然，严谨的来讲导函数为0的点是否为最大值还需要经过一些验证，这里就不验证了。求导过程比较简单，也不详细讲了，其中涉及到的矩阵求导可以参考matrix cookbook，这里直接给出结果：

\[\begin{align} \frac{\partial\mathcal{J}{(k)}(\sigma^2,\boldsymbol{\Gamma})}{\partial\gamma_i}= -\frac{1}{2\gamma_i}+\frac{1}{2\gamma_i^2}\boldsymbol{\Sigma_w}^{(k)}(i,i) +\frac{1}{2\gamma_i^2}[\boldsymbol{\mu}{(k)}(i)]^2 \tag{21} \end{align} \]

其中\(\gamma_i\)表示对角阵\(\boldsymbol{\Gamma}\)的第\(i\)个元素，\(\boldsymbol{\Sigma_{w}}^{(k)}(i,i)\)为\(\boldsymbol{\Sigma_{w}}^{(k)}\)的主对角线上第\(i\)个元素，\(\boldsymbol{\mu}{(k)}(i)\)为\(\boldsymbol{\mu}{(k)}\)的第\(i\)个元素。令式(21)为0可以得到：

\[\gamma_i^{(k+1)}=\boldsymbol{\Sigma_{w}}^{(k)}(i,i)+[\boldsymbol{\mu}_{(k)}(i)]^2 \tag{22} \]

其中\(\gamma_i^{(k+1)}\)为\(\boldsymbol{\Gamma}{(k+1)}\)的第\(i\)元素。\(\sigma^2{(k+1)}\)同理：

\[\begin{align} &\frac{\partial\mathcal{J}{(k)}(\sigma^2,\boldsymbol{\Gamma})}{\partial\sigma^2}= -\frac{N}{2\sigma^2}+\frac{1}{2(\sigma^2)^2} (||t-\Phi \boldsymbol{\mu}{(k)}||^2_2 +tr[\boldsymbol{\Phi\Phi}^h\boldsymbol{\Sigma_w}^{(k)}])=0\nonumber\\ &\sigma^2_{(k+1)}=\frac{||t-\Phi \boldsymbol{\mu}_{(k)}||^2_2 +tr[\boldsymbol{\Phi\Phi}^h\boldsymbol{\Sigma_w}^{(k)}]}{N} \tag{23} \end{align} \]

其中的\(tr[\boldsymbol{\Phi\Phi}^h\boldsymbol{\Sigma_w}^{(k)}]\)还可以写作\(\sigma^2_{(k)}tr[\boldsymbol{I}-\boldsymbol{\Gamma}_{(k)}^{-1}\boldsymbol{\Sigma_w}^{(k)}]\)，读者自证不难）。

至此我们已经完成了全部推导。

回顾式(17)到式(21)不难发现，实际进行EM算法求解的过程中并不需要真正的去求期望，和最大化损失函数，这些步骤已经蕴含在推导中了，而实际要做的只是根据(10)利用\(\sigma^2_{(k)}\)和\(\boldsymbol{\Gamma}{(k)}\)算出\(\boldsymbol{\mu}{(k)}\)和\(\boldsymbol{\Sigma_{w}}^{(k)}\)，再根据(22)和(23)算出\(\sigma^2_{(k+1)}\)和\(\boldsymbol{\Gamma}_{(k+1)}\)就行了。鉴于这仍然是两步走，所以第一步是实际中的E步，第二步为M步。

代码及结果

matlab 代码如下

function [w,ii] = sbl(t,Phi,gpu,sigma,Gamma)
	% t is the received signal
	% Phi is the dictionary
	% gpu means if you want to accelerate your code by gpu
	% sigma is the initial value of sigma, usually set 1
	% Gamma is the initial value of Gamma, usually set eye(M)
	% initial
	
	[N,M] = size(Phi);
	if(strcmp(gpu,'gpu'))
		t = gpuArray(t);
		Phi = gpuArray(Phi);
		Gamma = gpuArray(Gamma);
		matEyeN = gpuArray(eye(N));
		vecOne = gpuArray(ones(M,1));
	else
		matEyeN = eye(N);
		vecOne = ones(M,1);
	end
	
	%save the previous variable
	sigmaS = sigma;
	sigmaP = sigmaS;
	GammaP = Gamma;   
	
	ii = 0;
	iterErrNow = 100;
	
	while((iterErrNow>1e-2)&&(ii<200))
		ii = ii+1;
		% e-step
		Sigmat = sigmaS.*matEyeN + Phi*Gamma*Phi';
		Sigmaw = Gamma-Gamma*Phi'*Sigmat^(-1)*Phi*Gamma;
		mu = sigmaS^(-1).*Sigmaw*(Phi')*t;
		
		% m-step
		Gamma = diag(abs(diag(Sigmaw)+abs(mu).^2));
		sigmaS = abs((t-Phi*mu)'*(t-Phi*mu)+sigmaS*sum(vecOne-...
			diag(Gamma).^(-1).*diag(Sigmaw)))/N;
			
		% stop when variable's changes become small enough
		iterErrNow = norm(sigmaP-sigmaS)+norm(diag(GammaP)-diag(Gamma)); 
		
		sigmaP = sigmaS;
		GammaP = Gamma;
		
		w = mu;
	
	end
end

实验代码

% close all

%% parameter
N = 64;
M = 16*N;
fs = 1;
f = 0:1/M:(M-1)/M;
t = 0:N-1;
window = rectwin(N);
Phi = exp(2*pi*1i*t'*f);

%% signal module
% fx = 0.3*rand(1,3);
fx = [0.1,0.2,0.21];
a = 0.3+0.7*rand(3,1);
x = exp(2*pi*1i*t'*fx)*a;
x = x./sqrt(var(x));
SNR = 0;
noise = 2^(-0.5)*(randn(N,1)+1i*randn(N,1));
x = x + 10^(-SNR/20)*noise;
% x = x.*window;
xf = fft(x,M)/N;

fig = figure;
hold on
plot(0:1/M:(M-1)/M,20*log10(abs(xf)))

%% sbl
tic
[wEst,iterNum,sigma] = sbl(x,Phi,'gpu',2,eye(M));
toc
plot(0:1/M:(M-1)/M,20*log10(abs(wEst)))
scatter(fx,20*log10(a))
xlim([0,0.5])
ylim([-60,10])
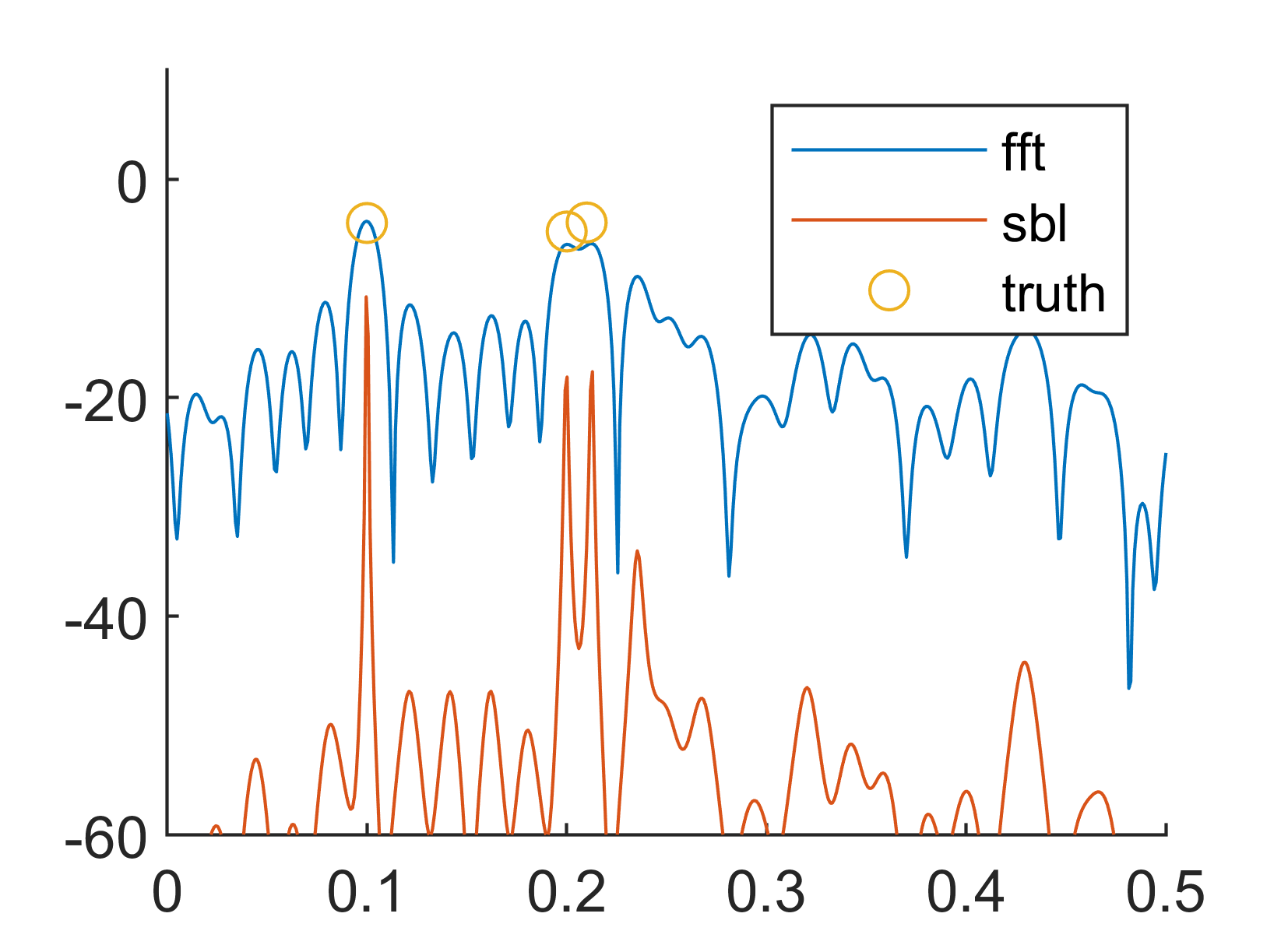
legend('fft','sbl','truth')

结果如下：

参考文献

1\]TIPPING M E. Sparse Bayesian Learning and the Relevance Vector Machine\[J\]. Journal of Machine Learning Research, 2001, 1(Jun): 211-244 \[2\]WIPF D P, RAO B D. Sparse Bayesian learning for basis selection\[J/OL\]. IEEE Transactions on Signal Processing, 2004, 52(8): 2153-2164. DOI:10.1109/TSP.2004.831016 \[3\] \[4\] \[5\][https://www.math.uwaterloo.ca/\~hwolkowi/matrixcookbook.pdf](https://www.math.uwaterloo.ca/~hwolkowi/matrixcookbook.pdf)