排序算法之基础排序:冒泡、选择、插入排序详解
- 前言
- [一、冒泡排序(Bubble Sort)](#一、冒泡排序(Bubble Sort))
-
- [1.1 算法原理](#1.1 算法原理)
- [1.2 代码实现(Python)](#1.2 代码实现(Python))
- [1.3 性能分析](#1.3 性能分析)
- [二、选择排序(Selection Sort)](#二、选择排序(Selection Sort))
-
- [2.1 算法原理](#2.1 算法原理)
- [2.2 代码实现(Java)](#2.2 代码实现(Java))
- [2.3 性能分析](#2.3 性能分析)
- [三、插入排序(Insertion Sort)](#三、插入排序(Insertion Sort))
-
- [3.1 算法原理](#3.1 算法原理)
- [3.2 代码实现(C++)](#3.2 代码实现(C++))
- [3.3 性能分析](#3.3 性能分析)
- 四、三种基础排序算法的对比与应用场景
- 总结
前言
排序算法是数据处理的基础且重要的组成部分,冒泡排序、选择排序和插入排序作为基础排序算法,虽然在效率上不及一些高级排序算法,但它们原理简单、易于理解,是学习排序算法的入门之选,也是理解更复杂排序算法的基础。本文我将详细介绍这三种基础排序算法的原理、实现代码、性能分析以及实际应用场景。
一、冒泡排序(Bubble Sort)
1.1 算法原理
++冒泡排序++的基本思想是重复地走访过要排序的数列,一次比较两个相邻的元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个过程就像水中的气泡,较小(或较大)的元素会逐渐 "浮" 到数列的顶端,因此得名冒泡排序。
具体过程如下:
比较相邻的元素。如果第一个比第二个大(升序排序),就交换它们两个。
对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
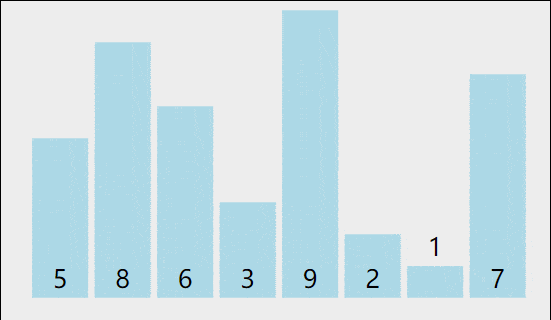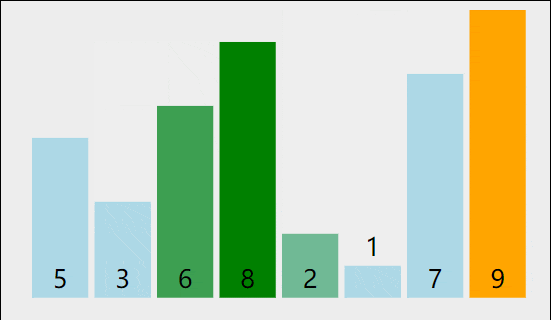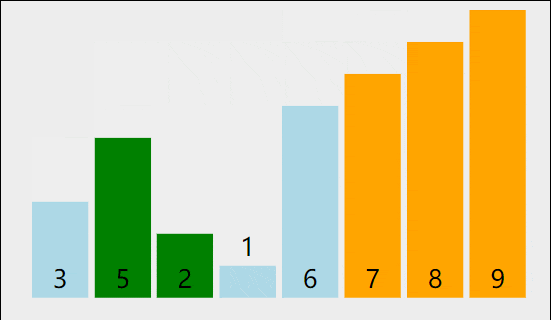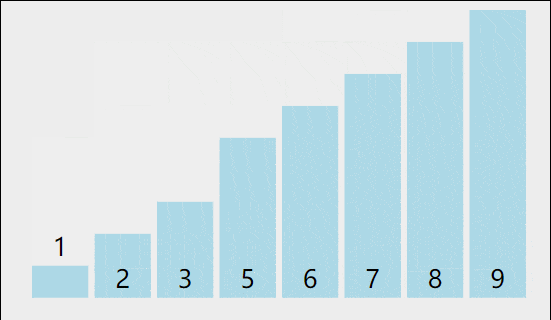
1.2 代码实现(Python)
python
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr在上述代码中,外层循环控制排序的轮数,一共需要n轮(n为数组长度)。内层循环用于每一轮中相邻元素的比较和交换,随着外层循环的进行,每一轮比较的次数逐渐减少,因为每一轮结束后,最大的元素已经 "沉" 到了数组末尾。
1.3 性能分析
时间复杂度:
最好情况:当数组已经是有序状态时,冒泡排序只需要进行一次遍历,比较n - 1次,不需要交换元素,时间复杂度为 O ( n ) O(n) O(n)。
最坏情况:当数组是逆序状态时,需要进行 n ( n − 1 ) / 2 n(n - 1) / 2 n(n−1)/2次比较和交换操作,时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
平均情况:时间复杂度同样为 O ( n 2 ) O(n^2) O(n2)。
空间复杂度 :冒泡排序只需要使用常数级别的额外空间来进行元素交换,空间复杂度为 O ( 1 ) O(1) O(1)。
稳定性:冒泡排序是一种稳定的排序算法,因为在比较和交换元素时,相同元素的相对顺序不会改变。
二、选择排序(Selection Sort)
2.1 算法原理
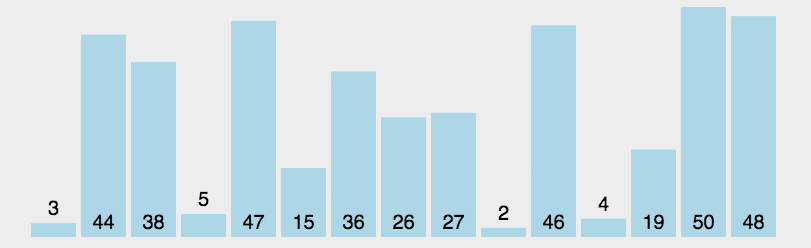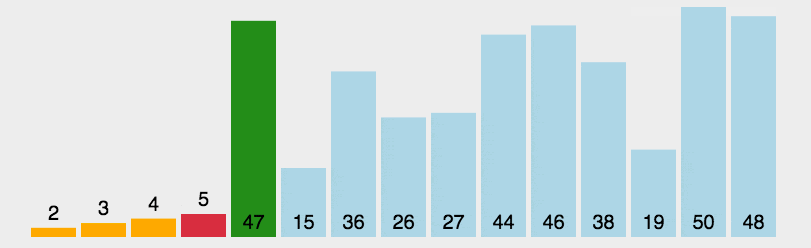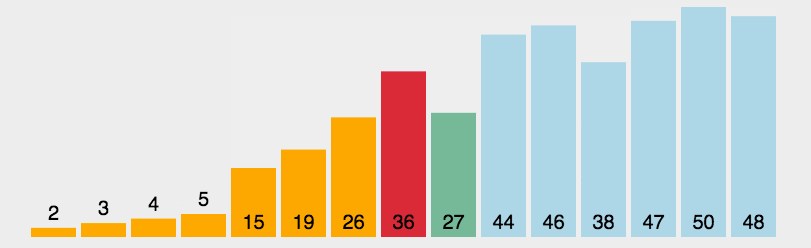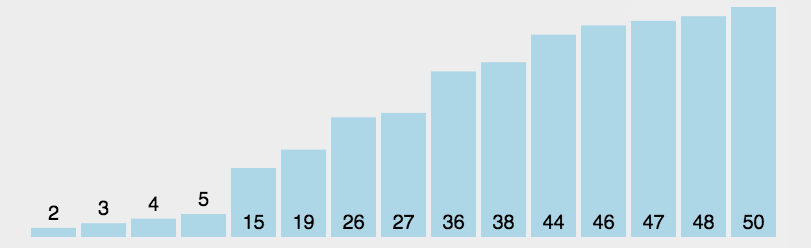
++选择排序++的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
具体步骤如下:
在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
2.2 代码实现(Java)
java
public class SelectionSort {
public static int[] selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
return arr;
}
public static void main(String[] args) {
int[] arr = {64, 25, 12, 22, 11};
int[] sortedArr = selectionSort(arr);
for (int num : sortedArr) {
System.out.print(num + " ");
}
}
}上述 Java 代码中,外层循环控制排序的轮数,一共需要n - 1轮(n为数组长度)。内层循环用于在每一轮中找到未排序部分的最小元素的索引,然后将其与当前轮起始位置的元素交换。
2.3 性能分析
时间复杂度:
最好情况:即使数组已经是有序的,选择排序也需要进行 n ( n − 1 ) / 2 n(n - 1) / 2 n(n−1)/2次比较,时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
最坏情况:同样需要进行 n ( n − 1 ) / 2 n(n - 1) / 2 n(n−1)/2次比较和交换操作,时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
平均情况:时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
空间复杂度 :选择排序只需要使用常数级别的额外空间来进行元素交换,空间复杂度为 O ( 1 ) O(1) O(1)。
稳定性 :选择排序是不稳定的排序算法,因为在选择最小元素并交换位置时,可能会改变相同元素的相对顺序。例如,数组[5, 5, 3],在排序过程中两个5的相对顺序可能会发生变化。
三、插入排序(Insertion Sort)
3.1 算法原理
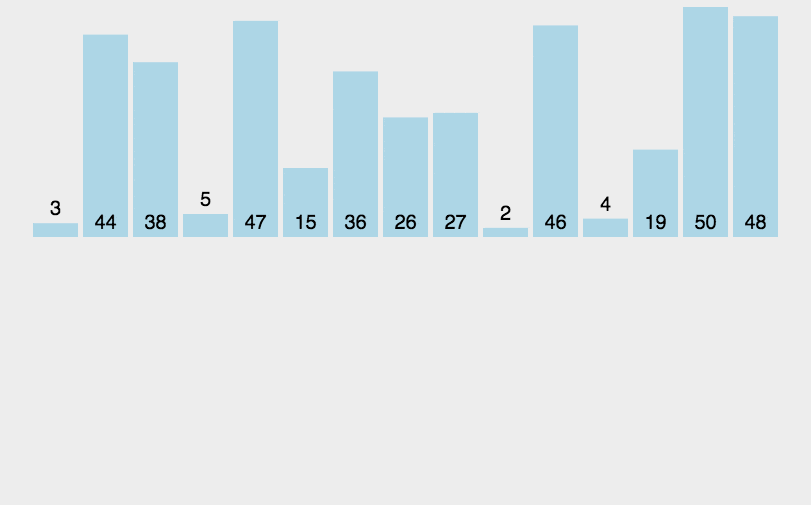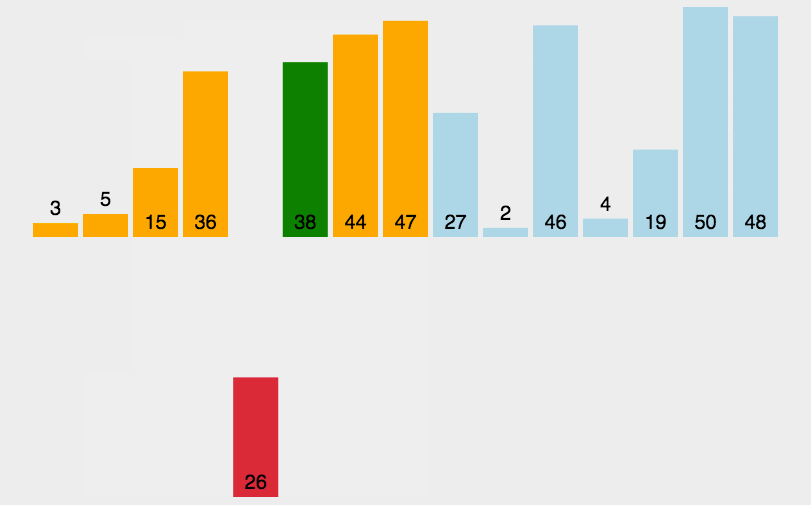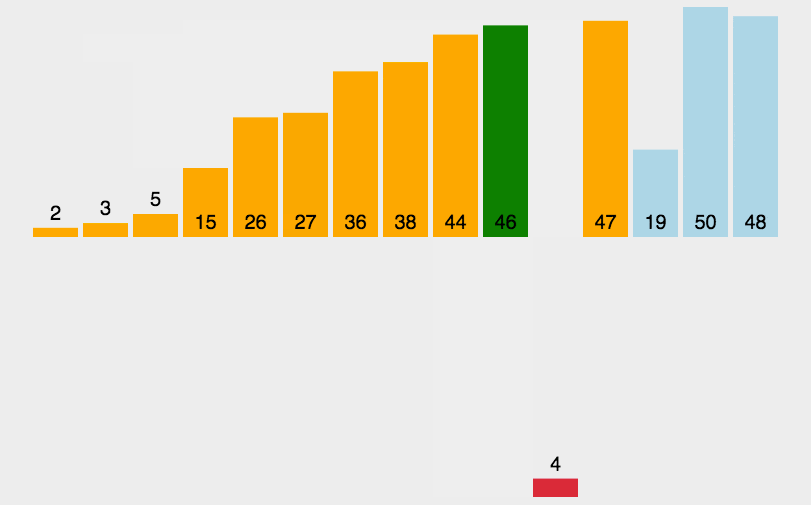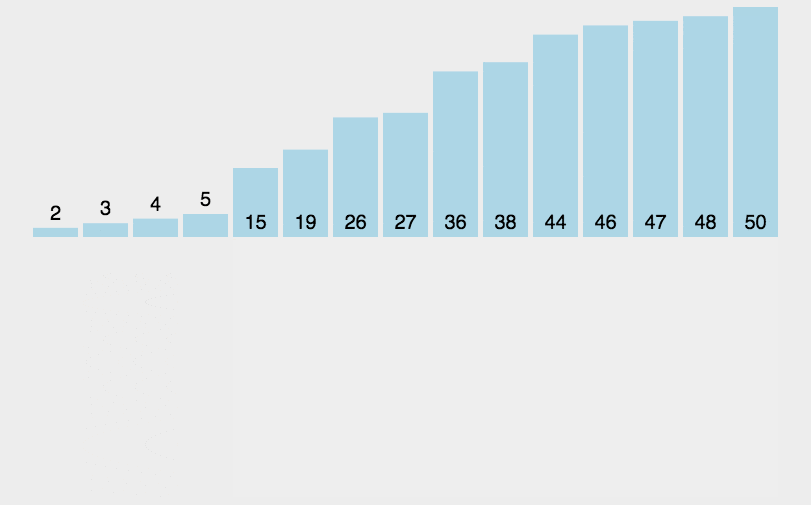
++插入排序++的基本思想是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据。其操作过程就像玩扑克牌时整理手中牌的过程,每次从 "牌堆" 中摸一张牌,插入到手中已整理好的牌的合适位置。
具体过程如下:
从第一个元素开始,该元素可以认为已经被排序。
取出下一个元素,在已经排序的元素序列中从后向前扫描。
如果该元素(已排序)大于新元素,将该元素移到下一位置。
重复步骤 3,直到找到已排序的元素小于或者等于新元素的位置。
将新元素插入到该位置后。
重复步骤 2~5,直到所有元素均排序完毕。
3.2 代码实现(C++)
cpp
#include <iostream>
#include <vector>
using namespace std;
vector<int> insertionSort(vector<int> arr) {
int n = arr.size();
for (int i = 1; i < n; ++i) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
return arr;
}在 C++ 代码中,外层循环从数组的第二个元素开始(因为第一个元素默认已排序)。内层循环用于在已排序部分中找到合适的插入位置,将当前元素插入到正确的位置,使得已排序部分始终保持有序。
3.3 性能分析
时间复杂度:
最好情况:当数组已经是有序状态时,每插入一个元素只需要比较一次,不需要移动元素,时间复杂度为 O ( n ) O(n) O(n)。
最坏情况:当数组是逆序状态时,插入每个元素都需要比较和移动i次(i为当前元素的索引),时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
平均情况:时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
空间复杂度 :插入排序只需要使用常数级别的额外空间来保存当前要插入的元素,空间复杂度为 O ( 1 ) O(1) O(1)。
稳定性:插入排序是稳定的排序算法,因为在插入元素时,相同元素的相对顺序不会改变。
四、三种基础排序算法的对比与应用场景
算法对比
| 排序算法 | 时间复杂度(最好) | 时间复杂度(最坏) | 时间复杂度(平均) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 插入排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
应用场景
冒泡排序:由于其简单易懂,常用于教学场景帮助初学者理解排序算法的基本概念。在数据规模较小且对时间要求不高的情况下,也可以使用。
选择排序:适用于对稳定性要求不高,且数据规模较小的排序场景。比如在一些简单的游戏内数据排序或者资源管理系统中,当数据量不大时可以使用。
插入排序:对于部分有序的数组或者数据量较小的数组,插入排序表现较好。例如,在数据库的某些索引维护操作中,如果数据更新后仍保持部分有序,插入排序可以高效地对新数据进行插入和排序。
总结
冒泡排序、选择排序和插入排序作为基础排序算法,虽然在时间复杂度上都为 O ( n 2 ) O(n^2) O(n2),在处理大规模数据时效率较低,但它们的原理简单,实现容易,是学习排序算法的重要基石。通过理解这三种算法,我们可以更好地掌握排序算法的基本思想,为学习更复杂高效的排序算法(快速排序、归并排序、堆排序等)打下坚实的基础。在下期博客中,我将深入探讨快速排序与归并排序这两种高效排序算法,详细解析它们的实现机制、性能特点以及在不同场景下的应用优势,帮助大家进一步拓宽对排序算法的认知边界。
That's all, thanks for reading!
创作不易,点赞 鼓励;
知识无价,收藏 备用;
持续精彩,关注不错过!