探秘Transformer系列之（34）--- 量化基础

[探秘Transformer系列之（34）--- 量化基础](#探秘Transformer系列之（34）--- 量化基础)
- [0x00 概述](#0x00 概述)
- [0x01 背景知识](#0x01 背景知识)
  - [1.1 需求](#1.1 需求)
  - [1.2 压缩](#1.2 压缩)
  - [1.3 如何表示数值](#1.3 如何表示数值)
  - [1.4 常见数据类型](#1.4 常见数据类型)
- [0x02 量化简介](#0x02 量化简介)
  - [2.1 深度神经网络的稀疏性](#2.1 深度神经网络的稀疏性)
    - [2.1.1 权重稀疏](#2.1.1 权重稀疏)
    - [2.1.2 激活稀疏](#2.1.2 激活稀疏)
    - [2.1.3 梯度稀疏](#2.1.3 梯度稀疏)
  - [2.2 量化机制](#2.2 量化机制)
    - [2.2.1 基本操作](#2.2.1 基本操作)
    - [2.2.2 范围映射](#2.2.2 范围映射)
      - 量化误差
      - 校准
      - [均匀量化 & 非均匀量化](#均匀量化 & 非均匀量化)
      - [Afﬁne Quantization & Scale Quantization](#Afﬁne Quantization & Scale Quantization)
      - [MinMax 量化 & 基于截断的量化](#MinMax 量化 & 基于截断的量化)
    - [2.2.3 量化比特](#2.2.3 量化比特)
    - [2.2.4 分类](#2.2.4 分类)
  - [2.3 量化对象](#2.3 量化对象)
    - [2.3.1 权重（和偏置）](#2.3.1 权重（和偏置）)
    - [2.3.2 激活](#2.3.2 激活)
    - [2.3.3 校准](#2.3.3 校准)
    - [2.3.3 量化粒度](#2.3.3 量化粒度)
      - 逐张量量化
      - [逐通道量化 & 逐token量化](#逐通道量化 & 逐token量化)
      - 逐组量化
      - 混合精度量化 (Hybrid Quantization)
    - [2.3.4 术语](#2.3.4 术语)
  - [2.4 量化工作流程](#2.4 量化工作流程)
    - [2.4.1 PTQ](#2.4.1 PTQ)
    - [2.4.2 QAT](#2.4.2 QAT)
    - [2.4.3 推荐流程](#2.4.3 推荐流程)
  - [2.5 加速原因](#2.5 加速原因)
    - [2.5.1 访存加速](#2.5.1 访存加速)
    - [2.5.2 向量化运算加速](#2.5.2 向量化运算加速)
    - [2.5.3 量化算子优化](#2.5.3 量化算子优化)
- [0xFF 参考](#0xFF 参考)

0x00 概述

虽然基于Transformer架构的LLMs已经取得了长足的发展，但由于LLMs的参数变得越来越多，部署基于Transformer的LLMs面临着重大挑战。例如，即使是中等规模的LLMs，如LLaMA13B，也需要大约26GB的内存来加载其所有参数的FP16格式。这样的开销不仅推高了使用成本，而且限制了它们的更广泛应用。

为了应对这些挑战，人们提出了许多针对LLMs的专业压缩方法，包括剪枝、知识传递、量化、紧凑的架构设计以及动态网络等。这些方法有助于减少模型推理过程中的内存和计算成本，以便模型可以在各种资源受限的设备上运行。模型量化（Model Quantization，也叫网络量化）则是模型压缩中的一项重要方法。模型量化过程分为两部分：将模型的单精度参数（一般 FP32-32位浮点参数）转化为低精度参数（一般 INT8-8 位定点参数），以及模型推理过程中的浮点运算转化为定点运算。模型量化技术可以降低模型的存储空间、内存占用和计算资源需求，从而提高模型的推理速度。

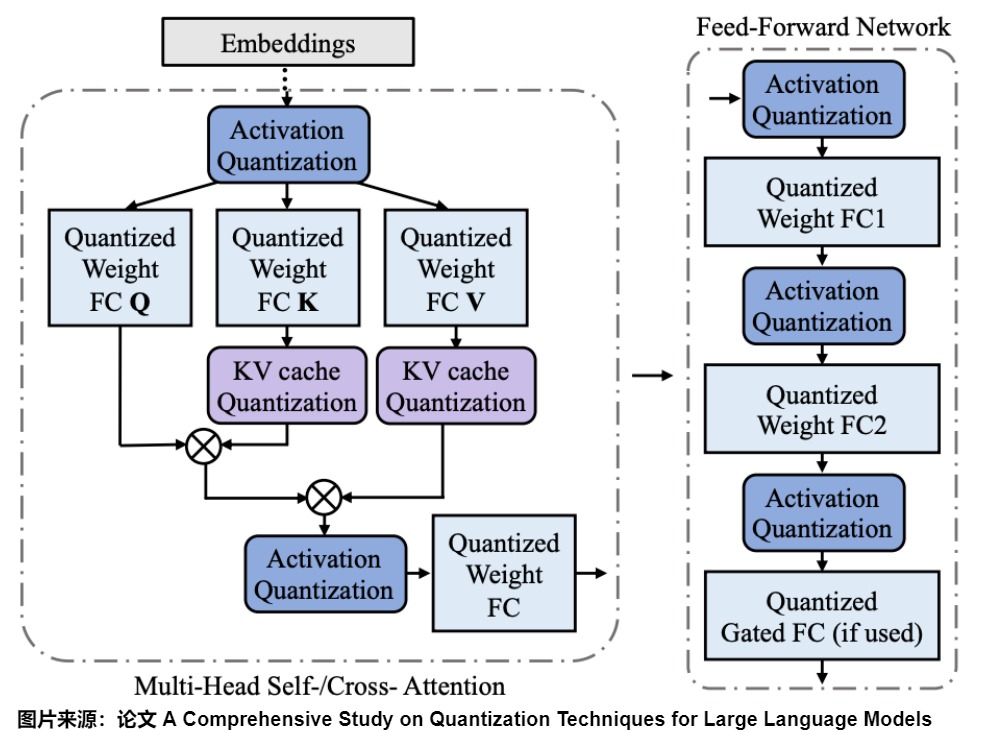
注：关于量化，一共有5篇，本文是第一篇。

0x01 背景知识

1.1 需求

在大语言模型的实际运行过程中，资源效率问题主要体现在显存压力和计算效率两个方面。这些问题随着模型规模的扩大和应用场景的复杂化而愈发突出。

显存压力：大语言模型在处理长文本时面临着严重的显存压力。这种压力体现在两个方面：
- 模型参数规模的增加。大型语言模型之所以得名，是因为它们包含的参数数量。这些模型通常拥有数十亿个参数，存储这些参数可能相当昂贵。在推理过程中，激活值是输入和权重的乘积，同样可能非常庞大，通常需要配备大量显存的GPU来加速推理过程。
- KV Cache的特性是随着输入序列长度的增加，所需显存呈线性增长。例如，在处理一个32K长度的文本序列时，仅KV Cache就可能占用10-15GB显存，这与模型本身的权重参数需要共享有限的显存空间。这种显存压力直接限制了模型处理超长文本的能力，也影响了系统的整体扩展性。
计算效率：显存资源的限制进一步导致了计算效率的下降。具体表现在三个层面：
- 批处理能力受限：由于显存占用，系统难以同时处理多个大批量请求。
- 响应延迟增加：特别是在处理长序列时，模型的推理时间显著延长。
- 系统吞吐量下降：受限于显存容量，服务器能够同时处理的请求数量大幅减少。

另外，不同的应用场景也带来了独特的挑战：

边缘计算环境下，需要在有限的计算资源中实现模型的高效运行。
移动设备应用要求模型能够适应严格的内存限制。
实时交互场景对模型的响应延迟提出了更高要求。

对于模型小型化，人们关注的是模型的平均推理时间和功耗, 平均推理时间可以用latency 或 throughput 来衡量, 而功耗则可以用参考生成token过程中所用到GPU的功耗。这两个指标都与模型参数量紧密相关, 特别是LLMs的参数量巨大, 导致部署消耗GPU量大。

综上所述，在部署过程中如何使得模型变得更小更轻，且保持模型能力尽可能不下降就成了一个重要的研究话题。

1.2 压缩

模型压缩算法可以将一个庞大而复杂的预训练模型转化为一个精简的小模型，减少对硬件的存储、带宽和计算需求，以达到加速模型推理和落地的目的。按照压缩过程对网络结构的破坏程度，有研究人员将模型压缩技术分为"前端压缩"和"后端压缩"两部分:

前端压缩，是指不改变原网络结构的压缩技术，主要包括知识蒸馏、轻量级网络（紧凑的模型结构设计）以及滤波器（filter）层面的剪枝（结构化剪枝）等；
后端压缩，是指包括低秩近似、未加限制的剪枝（非结构化剪枝/稀疏）、参数量化以及二值网络等，目标在于尽可能减少模型大小，会对原始网络结构造成极大程度的改造。

近年来主流的模型压缩方法包括：数值量化（Data Quantization，也叫模型量化），模型稀疏化（Model sparsification，也叫模型剪枝 Model Pruning），知识蒸馏（Knowledge Distillation），轻量化网络设计（Lightweight Network Design）和张量分解（Tensor Decomposition）。

1.3 如何表示数值

让我们首先看看在计算机中如何表示数值。因为神经网络的推理和训练都是计算密集型的。所以，数值的有效表示就显得尤为重要。

在计算机科学中，一个给定的数值通常表示为浮点数（或称为浮点），即带有小数点的正数或负数。这种表达方式利用科学计数法来表达实数。即用一个尾数（Mantissa，尾数，它实际上是有效数字的非正式说法），一个基数(Base)，一个指数(Exponent)以及一个表示正负的符号来表达实数。具体参见下图。

定点是另外一种数值的表示，它和浮点的区别在于，将整数（integer）部分和小数（fractional）部分分开的点在哪里。定点保留特定位数整数和小数，而浮点保留特定位数的有效数字（significand）和指数（exponent）。

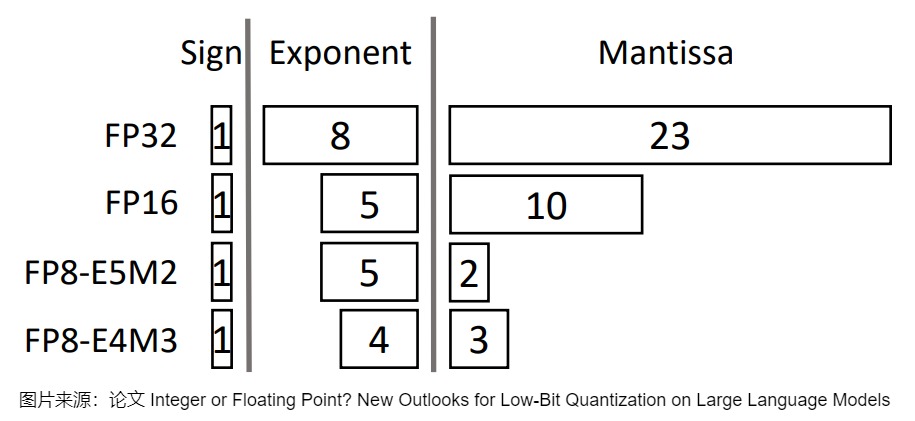由上图可知，尾数和指数由"位"或二进制数字表示，不同数据类型的尾数和指数不同，我们用越多的位来表示一个值，它通常就越精确。这些位的一个巧妙特性是，我们可以计算设备存储给定值需要多少内存。由于一字节内存中有8位，我们可以为大多数形式的浮点表示创建一个基本公式。

\[memory = \frac{number\_of\_bits}{8} \times number\_of\_params \]

现在假设我们有一个模型，包含700亿个参数。大多数模型默认使用32位浮点数（通常称为全精度）表示，仅加载模型就需要280GB的内存。

\[64\text{-}bits = \frac{64}{8} \times 70B \approx 560GB \\ 32\text{-}bits = \frac{32}{8} \times 70B \approx 280GB \\ 16\text{-}bits = \frac{16}{8} \times 70B \approx 140GB \\ \]

模型参数的位数（包括在训练期间）变得非常重要，因为其决定了模型占据的内存大小。但是随着精度的降低，模型的准确性通常也会下降。所以我们希望在保持准确性的同时减少表示数值的位数。

1.4 常见数据类型

我们再来看看常见的数据类型以及使用它们替代32位（称为全精度 或FP32）表示的影响。

常规精度模型把模型权重数值格式表示为 FP32（32位浮点，单精度）。
混合精度（Mixed precision）在模型中同时使用 FP32 和 FP16 的权重数值格式。FP16 减少了一半的内存大小，但有些参数或操作符必须采用 FP32 格式才能保持准确度。
低精度模型把模型权重数值格式表示为 FP16（半精度浮点）或者 INT8（8位的定点整数），目前业界正努力追求INT4和INT1的精度，而INT32或FP16的性能改进并不显著，所以INT8的量化是主要的选择。

另外，当我们在特定数据类型（如 INT8）中进行计算时，我们需要另一种数据类型的结构来保存结果，以便处理溢出，这叫做。累加数据类型（accumulation data type），比如INT8的accumulation data type是INT32。累加数据类型指定了相关数据类型值的累加（加法、乘法等）结果的类型。例如考虑两个 int8 值 A = 127、B = 127，并将 C 定义为 A 和 B 的和：

复制代码

C = A + B

这里的结果 C 远大于 int8 的最大可表示值 127，因此，我们需要一种精度更高的数据类型，以避免巨大的精度损失。比如bfloat16的累加数据类型就是float32。

下图给出了不同数据类型对应的累加数据类型、数学操作和带宽优化率。

0x02 量化简介

量化的核心思想是：在可接受的精度损失范围内，用更紧凑的数据格式来表示原始数据。

量化概念源自数字信号处理领域，指将信号的连续取值（或者大量可能的离散取值）近似为有限多个（或者较少的）离散值的过程。神经科学中与神经网络量化的研究表明，以连续形式存储的信息将不可避免地受到噪声的破坏，而且离散表示具有更高的泛化能力，以及在有限资源下具有更高的效率。所以人们普遍认为，人脑是以离散/量化形式存储信息，而不是以连续形式存储信息。

在机器学习中，模型量化是指将神经网络的浮点算法转换为低精度的整数以节省计算开销，比如使用 8 位整数（int8）等低精度数据类型来表示权重和激活度，而不是通常的 32 位浮点。减少比特数意味着生成的模型尺寸会减少、进而在推理时所需的内存存储更少，能耗更低。而且矩阵乘法等运算可以用整数算术更快地完成。因此，量化是一种降低推理计算和内存成本的有效技术。

神经网络模型可以量化有几点关键因素：

首先，神经网络的推理和训练都是计算密集型的。因此，数值的有效表示就显得尤为重要。
其次，大多数当前的神经网络模型都严重过度参数化，因此有足够的机会在不影响精度的情况下降低比特精度。
再次，神经网络对激进量化和极端离散化非常鲁棒。在量化模型与原始非量化模型之间具有较高的误差/距离的同时，仍然可以获得非常好的泛化性能。
最后，神经网络模型的分层结构提供了一个额外的维度来探索。神经网络中不同的层对损失函数有不同的影响，这激发了混合精度量化方法。

2.1 深度神经网络的稀疏性

根据深度学习模型中可以被稀疏化的对象，深度神经网络中的稀疏性主要包括权重稀疏，激活稀疏和梯度稀疏。

2.1.1 权重稀疏

在大多数神经网络中，通过对网络层（卷积层或者全连接层）对权重数值进行直方图统计，可以发现，权重数值分布很像正态分布（或者是多正态分布的混合），且越接近于 0，权重越多，这就是权重稀疏现象。有研究人员认为，权重数值的绝对值大小可以看做重要性的一种度量，权重数值越大对模型输出贡献也越大，反正则不重要，删去后对模型精度的影响应该也比较小。

2.1.2 激活稀疏

激活函数会造成激活的稀疏性。我们以ReLU 激活函数为例，其定义为：\(ReLU(x)=max(0,x)\) ，该函数使得负半轴的输入都产生 0 值的输出，这可以认为激活函数给网络带了另一种类型的稀疏性。即无论网络接收到什么输入，大型网络中很大一部分神经元的输出大多为零。

2.1.3 梯度稀疏

大多数深度神经网络模型参数的梯度其实也是高度稀疏的，论文"DEEP GRADIENT COMPRESSION: REDUCING THE COMMUNICATION BANDWIDTH FOR DISTRIBUTED TRAINING"发现，在分布式 SGD 算法中，99.9% 的梯度交换都是冗余的。

2.2 量化机制

我们接下来介绍一些量化相关知识点。

量化原理如下图所示。量化的主要目标是在尽可能保持原始参数的精度的同时，减少表示原始参数所需的位数。具体如下图所示，[-R, R] 是量化前的数据范围，[-127, 127] 是量化后的数据范围。这样就把模型权重等参数的精度从高位宽连续取值（通常为float32或者大量可能的离散值）降低到有限多个低位宽离散值（通常为int8）的过程。

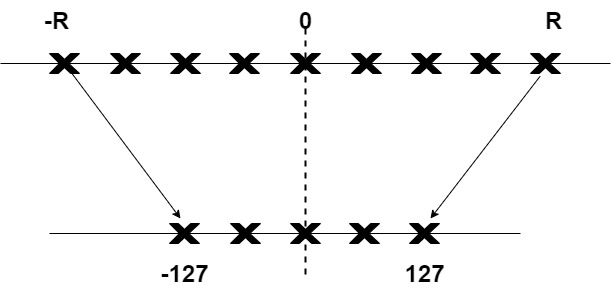
下图给出了量化公式。其中 X 是浮点张量，X¯是量化后的整数张量，Δ 是缩放系数，⌊⋅⌉ 表示四舍五入函数，N 为量化位数（此处为 8 位）。这里假设张量围绕 0 对称。该量化方法基于浮点数绝对值最大值来计算缩放系数 Δ，这会保留激活中的异常值，而这些异常值对模型的准确性至关重要。我们可以基于部分校准样本集的激活值离线计算缩放系数 Δ，这称为静态量化；也可以在模型运行时根据激活统计数据来动态计算缩放系数，这称为动态量化。

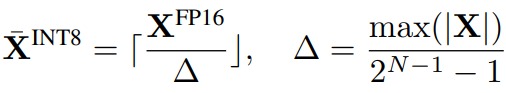
2.2.1 基本操作

量化有两个基本操作：

量化（quantization）：将数据转换为较低精度，比如将一个实数转换为一个量化的整数（float32 变成int8）。
反量化（ de-quantization）：将数据转换为较高精度。比如将一个数从一个量化的整数表示形式转换为一个实数（int8变成float32）。

具体如下图所示。我们会在接下来进行细致分析。

也可以进一步细化。下面(1)式是量化，(2)式是反量化。Q(·)表示量化操作，X代表输入tensor，S即为scale，Z即为zero-point，b为量化比特，round(⋅)和clip(⋅)分别表示取整和截断操作，\(q_{min}\)和\(q_{max}\)是量化后的最小值和最大值。S和Z统称为量化参数。多数的量化算法可以理解为就是为了找到更好的S和Z，使得量化模型的结果尽可能逼近原模型的结果.。

\[Q(X) = clamp(\lfloor\frac{X}{S}\rceil + Z, 0, 2^b -1)\tag {1}\\ \]

\[\hat X = (Q(X) - Z) \times S \tag{2} \]

假设r表示量化前的浮点数，量化后的整数q可以表示为：

\[q = clip(round(\frac{r}{s} + z), q_{min},q_{max}) \]

2.2.2 范围映射

量化过程的核心就是找到一个合适的映射关系，将浮点数映射到整数空间。这个映射需要保证：

能够覆盖原始数据的完整范围。
尽可能保持数值的相对关系。
保证量化后的数值都落在某个表示范围内，比如INT8是0-255。

在范围映射中，必须将范围[A1, A2]的数据转换为B位整数的范围。具体而言，是将范围[A1, A2]中的所有元素映射到目标范围中，超出[A1, A2]范围的元素将被剪切到最接近的边界。比如，我们需要将FP32映射到int8范围内，int8 只能表示 256 个值，而 float32 可以表示的值范围更广。而一般神经网络层权重的值分布范围很窄，但是在这值域中数值点数量却很大。所以需要仔细调整范围映射，才能更好地将float32值范围 [a, b] 投射到 int8 空间。

量化误差

大部分模型量化的使用者或者研究者，更关注的是量化模型的精度问题。模型量化将更高数值精度的浮点模型转换为少数的离散定点，不可避免会引入误差。而在神经网络模型中，每一层的量化误差传递放大，就会导致量化模型精度过低。一般定义量化操作为： \(\hat{X} = Round( clamp(\frac{X}{s}, Q_{min}, Q_{max}) )\)，其中 Round 表示舍入操作，clamp 截断超过量化域范围 \(\left [ Q_{min}, Q_{max} \right ]\) 的异常值。Round 和 Clamp 操作都会导致数值精度的不可逆损失，简单来说，一个tensor 的量化误差可以表示为截断误差和舍入误差之和。而这两者又是相关联的，s 表示缩放因子，定义为 \(s = \frac{X_{max} - X_{min} }{2^{bit}-1 }\) ，也就是说它是通过截断的上下界来决定。综合两者可以得到一个经验公式 \(\sigma ^{2} ～ \frac{s^{2} }{12}\)，即量化误差正比于 \(s^{2}\) 。

校准

为了计算 scale 和 zero_point，我们需要知道 FP32 weight/activation 的实际动态范围。校准就是选择一个最优范围的过程，即找到一个能包含尽可能多的值，同时又能最小化量化误差的范围。校准对有效的量化至关重要。对于推理过程来说，weight 是一个常量张量，动态范围是固定的，activation 的动态范围是变化的，它的实际动态范围必须经过采样获取（数据校准）。如果量化过程中的每一个 FP32 数值都在这个实际动态范围内，我们一般称这种为不饱和状态；反之如果出现某些 FP32 数值不在这个实际动态范围之内我们称之为饱和状态。

均匀量化 & 非均匀量化

从范围映射角度来看，根据量化数据表示的原始数据范围是否均匀，可以将量化方法分为均匀量化&非均匀量化。实际的深度神经网络的权重和激活值通常是不均匀的，因此理论上使用非线性量化导致的精度损失更小，但在实际推理中，非线性量化的计算复杂度较高，所以我们通常使用线性量化。

非均匀量化（也称为非线性量化）。非均匀量化定义如下图所示，当实数 r 的值落在量化步长 \(\Delta_i\) 和\(\Delta_{i+1}\) 之间时，量化器Q将其投影到相应的量化级别\(X_i\)，\(X_i\)和\(\Delta_i\)的间距都是不均匀的。对于固定位宽，非均匀量化可以实现更高的精度，因为可以通过更多地关注重要值区域或找到适当的动态范围来更好地捕获分布。例如，许多非均匀量化方法是针对权重和激活的钟形分布而设计的，这些分布通常涉及长尾。典型的基于规则的非均匀量化是使用对数分布，其中量化步长和级别呈指数增长而不是线性增长。
均匀量化（也称为线性量化）。线性量化采用均匀分布的聚类中心，原始浮点数据和量化后的整数存在一个简单的线性变换关系。因为卷积、全连接等网络层本身只是简单的线性计算，因此线性量化中可以直接用量化后的数据进行直接计算。均匀量化将实数值范围划分为均匀的有限区间，然后，同一区间内的实数值被映射到相同的整数。其实，均匀量化得到的量化值（又称量化级别）也是均匀的。

下图给出了均匀量化（左）和非均匀量化（右）之间的比较。连续域 r 中的实数值被映射到量化域Q中的离散、较低精度值，这些值用橙色点来标记。请注意，在均匀量化中，量化值（量化级别）之间的距离是相同的，而在非均匀量化中它们可以变化。

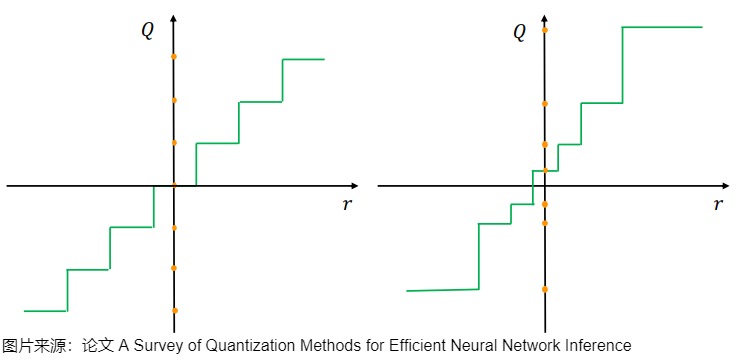
神经网络的权重通常不是均匀分布的，因此非均匀量化是可行的。一般来说，非均匀量化使我们能够通过非均匀地分配比特和离散化参数范围来更好地捕获信号信息，可以提供更高的精度和更低的量化误差。然而，非均匀量化方案可能会因为涉及耗时的查找操作而效率低下，通常难以在通用计算硬件（例如 GPU 和 CPU）上有效部署。因此，均匀量化由于其简单性和到硬件的高效映射而成为目前事实上的标准方法。

Afﬁne Quantization & Scale Quantization

均分量化即Uniform quantization分两步：

选择要量化的数值（浮点）的范围并截断，截断的意义是：大于数值范围的就让其为数值范围的最大值，小于数值范围的就变成数值范围的最小值。
将截断后的数值映射到整数上，这一步有round的操作。

设\([\beta,\alpha]\)是为量化选择的可表示实值的范围，b是带符号整数表示的位宽（bit-width）。均匀量化将输入值\(x\in[\beta,\alpha]\)变换到\([-2^{b-1}, 2^{b-1}-1]\)内，其中范围外的输入被截断到最近的边界。

由于我们只考虑均匀变换，因此根据量化前后浮点空间中的零的量化值是否依然是 0，可以将浮点数的线性量化分为两类：对称量化 Symmetric Quantization 和非对称量化 Asymmetric Quantization。我们将这两种选择分别称为scale和afﬁne。对应变换函数也是两种选择：f(x) = s · x + z及其特例 f(x) = s · x。

Scale Quantization：变换函数是 f(x) = s · x, 即对称量化，s 是缩放因子。Scale Quantization的特点如下：
- 对称量化就是将一个张量中的 [−𝑚𝑎𝑥(∣𝑥∣), 𝑚𝑎𝑥(∣𝑥∣)] 内的 FP32 值分别映射到 8 bit 数据的 [−128,127] 的范围内，中间值按照线性关系进行映射。可以看出，对称量化的浮点值和量化值范围都是相对于零对称的，所以叫对称量化。
- 在对称量化中，原始浮点值的范围被映射到量化空间中以零为中心的对称范围。对于int8，那么int8的值域范围就是[-127, 127]，不适用128这个数值。对称量化的一个很好的例子被称为绝对最大值（absmax）量化。给定一系列值，我们取最大的绝对值（α）作为执行线性映射的范围。
- 对称量化可以避免量化算子在推理中计算z相关的部分，降低推理时的计算复杂度；在解量化步骤中，对称量化的计算效率更高，实现起来更简单。
- 对称量化在量化权重的实践中被广泛采用，因为将零点归零可以减少推理过程中的计算成本，并且使实现更加简单。
- 将对称量化在用到激活上时有疑问，因为激活值常常为非负值。因为量化区间大多落在非负区间，浪费了量化范围，增大了量化误差。
- 对权值和数据的量化可以归结为寻找 𝑠𝑐𝑎𝑙𝑒 的过程，量化方法的改进本质上是选择最优 𝑠𝑐𝑎𝑙𝑒 值的过程。
Afﬁne Quantization：变换函数是 f(x) = s · x + z，即非对称量化，s是缩放因子，z是零点。Afﬁne Quantization的特点如下：
- 非对称量化的裁剪范围不一定是相对于原点对称的。它将浮点范围中的最小值（β）和最大值（α）映射到量化范围的最小值和最大值。这样可以利用到整个量化范围，但是计算更复杂。比如，对于int8，那么int8的值域范围就是[0,255]。
- 非对称算法一般能够较好地处理数据分布不均匀的情况。与对称量化相比，非对称量化通常导致更窄的裁剪范围，这对激活可能严重失衡的神经网络中的激活尤为重要。例如，ReLU之后的激活总是具有非负值，这个情况下还是用对称量化就会浪费一个bit的表示能力，只能[0, 127]。非对称量化可以根据实际数据的分布确定最小值和最小值，可以更加充分的利用量化数据信息，使得量化导致的损失更低。
- 权重参数的非对称量化算法可以分为两个步骤：
  - 通过在权重张量中找到 min 和 max 值，从而确定缩放系数 s 和零点偏移值 z。
  - 将权重张量的每个值从 FP32 转换为 INT8。

具体参见下图。round(⋅)和clip(⋅)分别表示取整和截断操作，s是数据量化的间隔，z是表示数据偏移的偏置。

下图给出了对位宽（bit-width）为8的不同均匀量化的直观解释。s是缩放因子，z是零点。浮动点网格(ﬂoating-point grid）为黑色，整数量化网格（integer quantized grid）为蓝色。

MinMax 量化 & 基于截断的量化

剪切范围和校准是均匀量化中的一个重要因素，选择合适的剪切范围可以减少异常值的数量，但也会导致更大的尺度系数和量化误差。根据实际值是否被截断（clipped），均匀量化又可以分为两类：保留所有值范围的 MinMax 量化和基于截断（clipping-based）的量化。

MinMax量化虽然允许将向量值的完整范围映射出来，但它带来了一个主要的缺点：异常值。如果原始数据中一个值比其他所有值都大得多，该值可以被认为是一个异常值。如果我们要把异常值映射到这个完整范围内，所有小的值都会被映射到相同或者相似的较低位表示，并且失去它们的差异信息。比如下图，因为500这个异常值的存在，导致 -255~255 这些数被映射到更小的范围内。

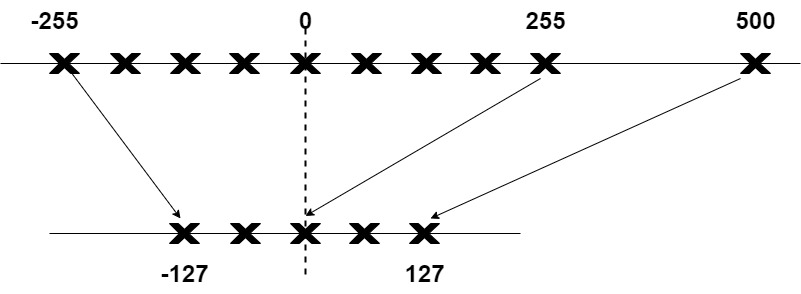
所以我们可以选择裁剪某些值，也就是定义一个自定义的动态范围，把极端值排除在外。裁剪会设置原始值的不同动态范围，任何超出这个范围的值都会被"裁剪"，不管它实际有多大，都被映射到目标范围的最大值或最小值。在下面的例子中，手动将动态范围设置为[-255,255]，那么所有超出该范围的值将被映射到-127或127，无论它们的实际值如何。

与 MinMax 量化相比，截断异常值有助于提高精度并为中间值分配更多位，显著降低了"非异常值"的量化误差。但是会导致离群值的量化误差增大。

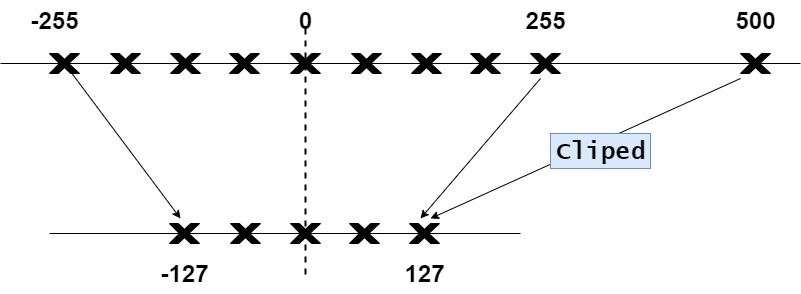
在现有截断算法中，截断值往往基于一个给定的数值，缺乏对数据实际分布的学习能力。为此，可以采用可学习的截断方式，即通过构建最小化单层量化MSE模型，求解得到截断参数 t的最优值。

2.2.3 量化比特

计算机中不同数据类型的占用比特数及其表示的数据范围各不相同。可以根据实际业务需求将原模型量化成不同比特数的模型，用来量化的比特数越少，量化后的模型压缩率越高。工业界目前最常用的量化位数是8比特，低于8比特的量化被称为低比特量化。1比特是模型压缩的极限，可以将模型压缩为1/32，在推理时也可以使用高效的XNOR和BitCount位运算来提升推理速度。下图给出了量化原理以及1bit和2bit的公式。

2.2.4 分类

论文"LLMC: Benchmarking Large Language Model Quantization with a Versatile Compression Toolkit"从数学角度把量化算法做如下分类。"Trans."指示算法是否是等效变换。γ是比例因子。s和Q表示变换向量和矩阵。I是恒等矩阵。L是具有学习率η的损失函数。α和β表示剪切最小值和最大值。H是Hessian矩阵，E表示用H计算的量化误差。λ是衰减系数。

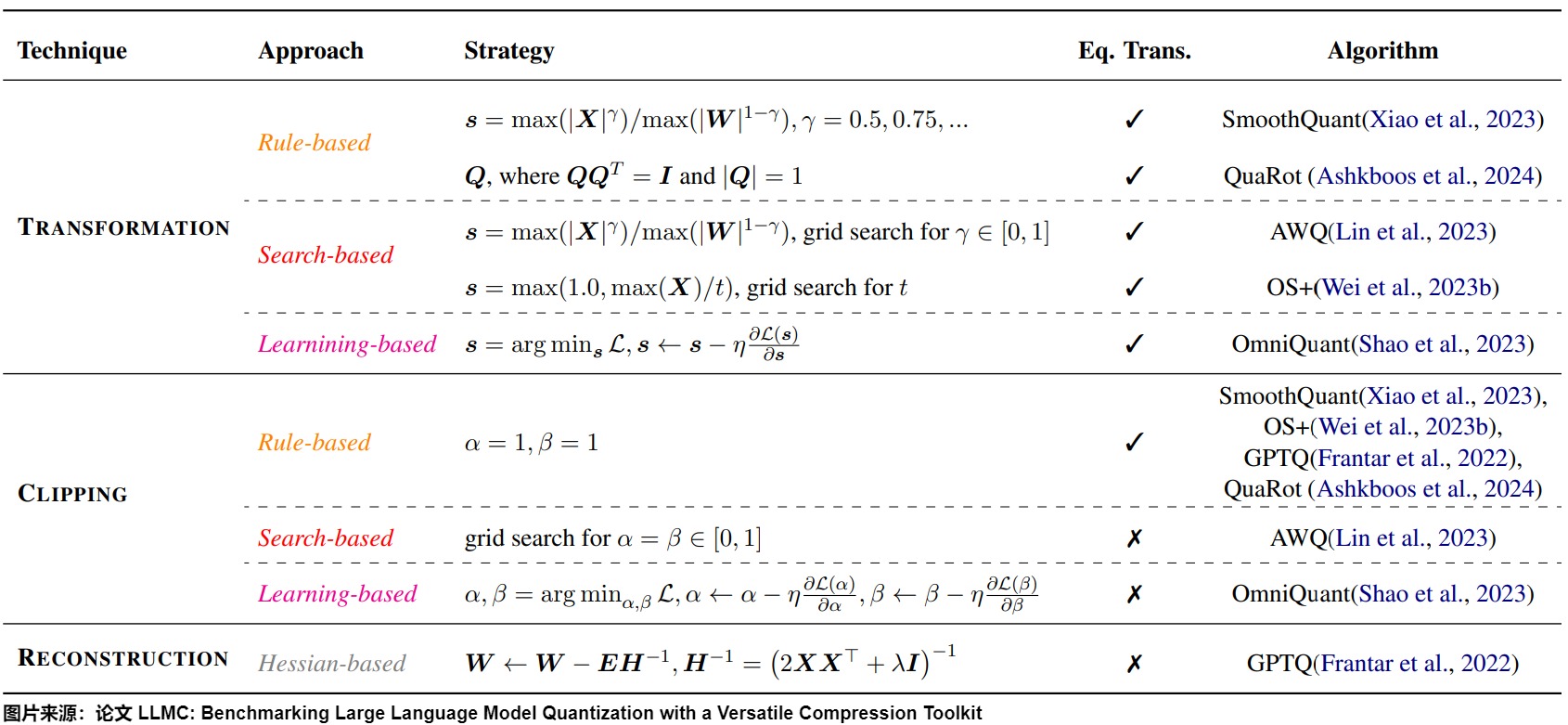
2.3 量化对象

模型量化的对象主要包括以下几个方面：

权重（weight）：weight的量化是最常规也是最常见的。量化weight可达到减少模型大小内存和占用空间。
激活（activation）：实际中activation往往是占内存使用的大头，因此量化activation不仅可以大大减少内存占用。更重要的是，结合weight的量化可以充分利用整数计算来获得性能提升。
梯度（Gradients）：在训练深度学习模型时，梯度通常是浮点数，因此量化梯度的主要作用是在分布式计算中减少通信开销，同时，也可以减少backward时的开销。因为主要用于训练，梯度量化相对上面两者略微小众一些，顾略过。
KV Cache：量化 KV Cache对于提高长序列生成的吞吐量至关重要。我们会在后续章节进行深入分析。

2.3.1 权重（和偏置）

权重量化仅量化模型的权重以压缩模型的大小，在推理时将权重反量化为原始的float32数据，后续推理流程与普通的float32模型一致。权重量化的好处是在某些需求中可以不需要校准数据集，不需要实现量化算子，且模型的精度误差较小。由于实际推理使用的仍然是float32算子，所以推理性能不会提高。由于偏置的数量（百万级）远少于权重（十亿级），偏置通常保持较高的精度（如INT16），因此量化的主要工作集中在权重上。

2.3.2 激活

因为模型主要由权重和偏置组成，在运行模型之前就已知这些值，因此我们可以将LLM的权重和偏置视为静态值。与权重不同，激活会随着在推理过程中输入模型的每个数据和层的不同而变化，这使得准确量化它们变得具有挑战性。由于这些值在每个隐藏层之后更新，所以只有在输入数据通过模型时才能知道它们在推理过程中的状态。为了量化激活值，需要用户提供一定数量的校准数据集用于统计每一层激活值的分布，并对量化后的算子做校准。校准数据集可以来自训练数据集或者真实场景的输入数据，需要数量通常非常小。

2.3.3 校准

可选择范围的校准技术主要包括：

max-min（最大最小值）：这是使用最简单也是较为常用的一种采样方法。基本思想是直接从 FP32 张量中选取最大值和最小值来确定实际的动态范围。对 weights 而言，这种采样方法是不饱和的，但是对于 activation 而言，如果采样数据中出现离群点，则可能明显扩大实际的动态范围，比如实际计算时 99% 的数据都均匀分布在 [-100, 100] 之间，但是在采样时有一个离群点的数值为 10000，这时候采样获得的动态范围就变成 [-100, 10000]。
滑动平均最大最小值(MovingAverageMinMax)：与 MinMax 算法直接替换不同，MovingAverageMinMax 会采用一个超参数 c (Pytorch 默认值为0.01)逐步更新动态范围。这种方法获得的动态范围一般要小于实际的动态范围。
KL散度（KL divergence）：最小化原始值和量化值之间的分布差异（KL散度）。一般认为量化之后的数据分布与量化前的数据分布越相似，量化对原始数据信息的损失也就越小，即量化算法精度越高。KL 距离(也叫 KL 散度)一般被用来度量两个分布之间的相似性。TensorRT 使用 KL 散度算法进行量化校准的过程：首先在校准集上运行 FP32 推理，然后对于网络每一层执行以下步骤：
1. 收集激活输出的直方图。
2. 生成许多具有不同饱和度阈值的量化分布。
3. 选择最小化 KL_divergence(ref_distr, quant_distr) 的阈值 T，并确定 Scale。
百分比（Percentile）：手动选择输入范围的百分位数，比如选取tensor的99%或者其他百分比的数值，其余的截断。也就是说，不是使用最大/最小值，而是使用第i个最大/最小值作为β/α。
MSE：优化原始权重和量化权重之间的均方误差。

2.3.3 量化粒度

量化方法的一个关键点是如何为权重计算所裁剪范围[α， β]的粒度。所谓量化有不同的粒度其实是指基于不同的粒度去计算量化缩放系数，即多大数据共享同一个缩放因子。一般来说，更细的粒度可以减少量化误差，但需要存储更多的量化参数并引入更高的计算开销。

量化粒度对应于哪些权重/激活一起量化并共享量化参数。按照量化粒度，我们可以把模型的量化分为逐向量量化（per-tensor）、逐token量化、逐通道（per-channel）量化和逐组量化（per-group）等。

逐张量量化

逐张量量化（per-tensor）也叫做逐层量化，这是最简单的一种方式，也是最粗粒度的量化方式。

该方案以一层网络为量化单位，每层网络一组量化参数（S和Z），比如整个激活矩阵的张量计算出一个统一的缩放因子（scale factor）；整个权重矩阵也是如此。后将张量中的所有元素都使用这个缩放因子量化到低精度格式，例如 INT8。因此也叫逐层量化（Layerwise）。例如，一个 INT8 的 per-tensor 动态量化器会找到整个张量的最大绝对值，以此计算出一个缩放因子，然后将所有元素缩放到 INT8 的表示范围内 [-127, +127] 并进行取整。

在大多数计算机视觉任务中，层的激活输入与许多不同的卷积过滤器进行卷积，如下图所示。每个卷积滤波器都可以有不同的取值范围。而逐层量化会对对属于同一层的所有卷积滤波器使用相同的裁剪范围。虽然这种方法很容易实现，但由于每个卷积滤波器的范围可能变化很大，它通常会导致次优精度。例如，一个参数范围相对较窄的卷积核（例如下图中的Filter 1）可能会因为同一层中另一个范围更大的核而失去其量化分辨率。

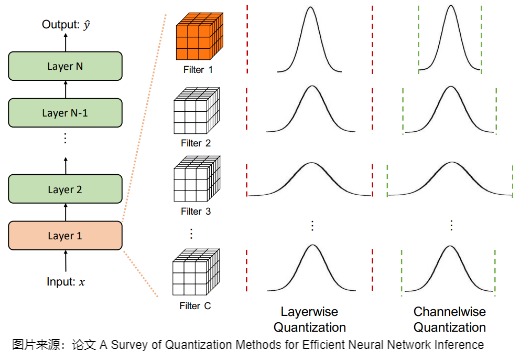
逐通道量化 & 逐token量化

逐张量量化是整个矩阵共用一个缩放系数，而逐 token 量化和逐通道量化则为每个 token 或权重的输出通道设定不同的缩放系数。

per-channel（channel就是维度，类似于embedding的维度，或者hidden size）。逐通道量化如上面卷积示例图最后一列所示。也就是说，以每一层网络的每个量化通道为单位，给每个通道都分配了一组独立的量化参数。逐通道量化由于量化粒度更细，能获得更高的量化精度，但计算也更复杂。以LLM来说，逐通道量化通常是针对权重而言，每列（通常指 hidden dim 维度的一列）对应一组量化系数。
per-token与逐通道量化类似，但，是针对激活（token就是文字的token）而言，每行（每个token）对应一组独立的量化参数。

当进行矩阵乘法时，可以通过组合各种技巧，例如逐行或逐向量量化，来获取更精确的结果。具体参见下图。图左侧是对于激活X和权重W都进行逐向量量化，即用整个矩阵张量的最大绝对值对张量进行归一化。右侧则使用逐token量化和逐通道量化混合进行。找到 X 的每一行和 W 的每一列的最大绝对值，然后逐行或逐列归一化 X 和 W 。最后将 X 和 W 相乘得到 C。最后，我们再计算与X 和 W 的最大绝对值向量的外积，并将此与 C 求哈达玛积来反量化回 FP16。

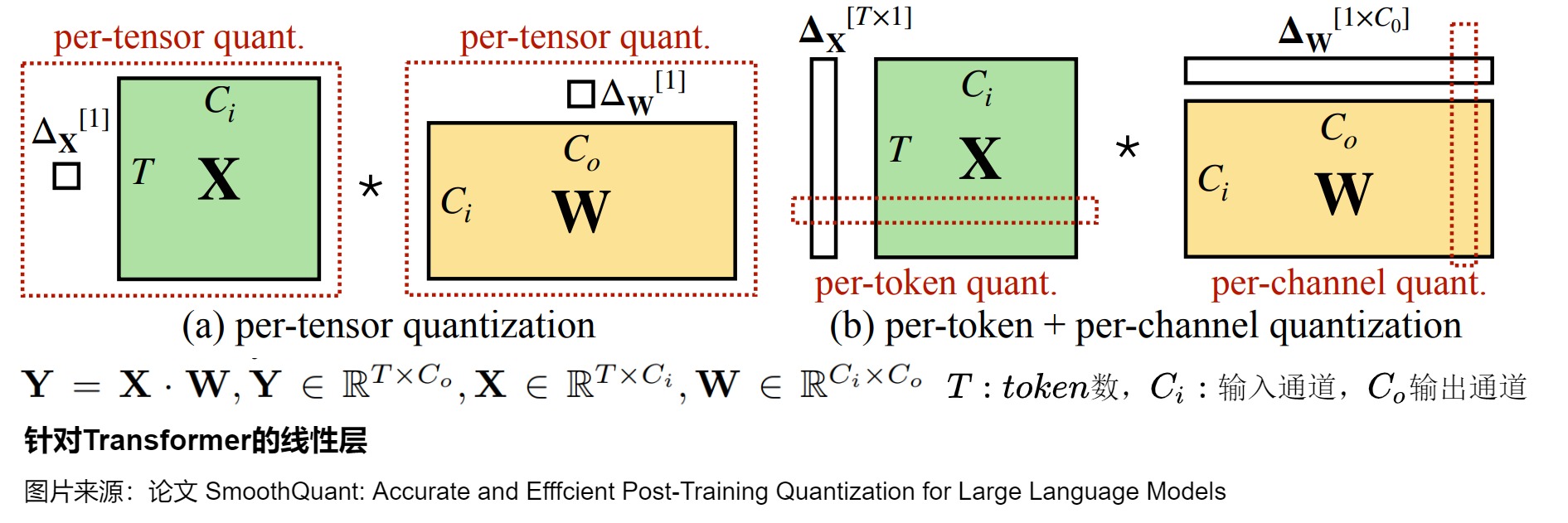
逐组量化

per-channel 量化的一个粗粒度版本是为不同的通道组使用不同缩放系数。逐组量化以组为单位，每个group使用一组S和Z；它的粒度处于 per-tensor 和 per-channel 之间。K行（对应激活）或者K列（对应权重）共享一个量化系数。当 group=1 时，逐组量化与逐层量化等价；当 group=num_filters（如：dw（Depthwise）将卷积核变成单通道）时，逐组量化与逐通道量化等价。

对于卷积示例图来说，可以在一个层内分组多个不同的通道来计算裁剪范围（激活或卷积核）。这对于参数在单个卷积/激活中的分布变化很大的情况很有帮助。然而，这种方法不可避免地带来了考虑不同缩放因子的额外成本。

下图给出了per-token和group-wise的对比。

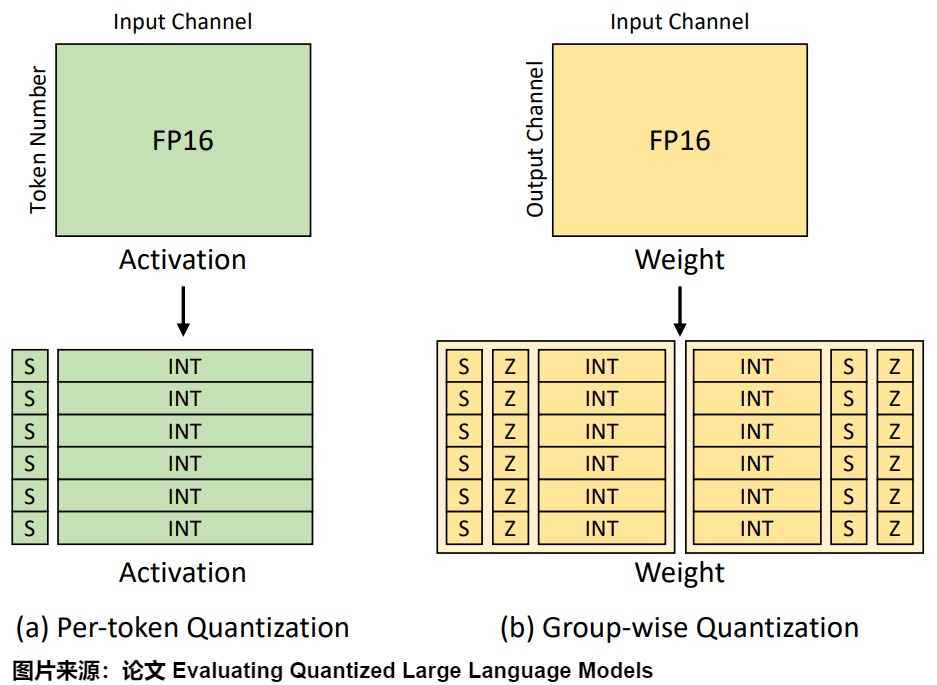
我们再看看OpenPPL-LLM的方案和思考。

OpenPPL-LLM引入两种不同的量化技术，即Groupwise量化(（通常为int4量化）与Channelwise量化（通常为INT8量化）。如下图所示，对于一个4x4矩阵而言，Groupwise量化将相邻的两个元素视作一组（图中颜色相同的元素为一组），组内元素共享量化参数。由于组内元素数量很少，这种量化方案具有较高量化精度，但将为系统带来更大的计算负担与访存开销。Channelwise量化将矩阵的每一列元素视作一组，每列元素共享量化参数，这种方案量化精度稍差，但其访存模式利于tensor core的运算，可以充分利用GPU的低精度运算器加速运算。这两种量化方式都可以起到压缩显存的作用。

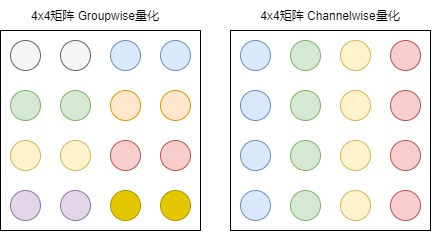
针对batchsize<16的推理场景，大语言模型中的所有计算任务都是访存密集型的，系统的运行瓶颈不在于计算，参数访存量远远超过激活访存。因此非常适合使用Groupwise量化的方式单独压缩矩阵乘法的参数矩阵，其计算和输入输出仍然保持FP16精度。这种量化将提供更高的量化精度。groupwise量化所带来的额外计算量也不会拖慢系统整体的运行效率。

针对batchsize>16的推理场景，groupwise的量化方式无法起到加速作用，此时系统的计算负载将逐渐转变为计算密集型的，我们必须利用GPU上具有更高算力的低精度运算器(int8 Tensorcore)加速网络执行。Groupwise量化并不利于GPU TensorCore的运行，这种量化方式将导致严重的访存不连续，因此性能很差。此时推荐以Channelwise量化的方式同时对矩阵乘法的输入和参数矩阵进行量化。

需要注意的是，Groupwise量化与Channelwise量化对应着不同的权重预处理过程，这两种方案必须在服务启动时加以确定，不能在模型运行时动态切换。因此我们需要在服务部署之初就确定量化模式的选择。

混合精度量化 (Hybrid Quantization)

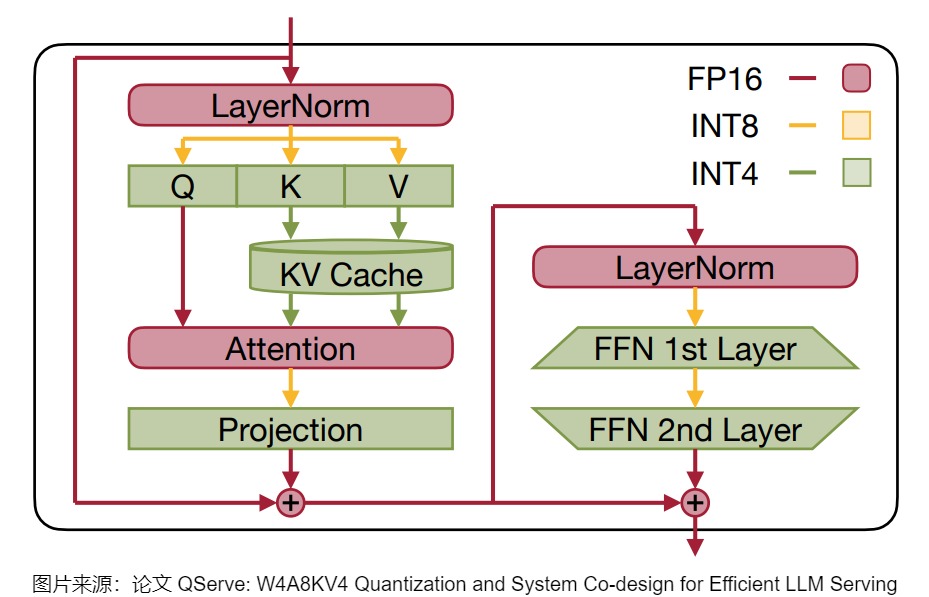
混合精度量化是一种更灵活的量化策略，它允许模型的不同部分使用不同的位宽进行量化。在大模型量化的过程中，不同的线性层对量化的敏感程度不同。基于此，混合精度量化对所有线性层进行敏感程度分类，将敏感层回退到更高精度计算，而对非敏感层做低精度量化计算。在量化前，通过随机采样生成校准集，并采集所有线性层的激活值，计算"四分位比例"统计量。

2.3.4 术语

我们接下来看看术语。

以W1A16为例：W1A16指的是一种特定的量化设置，这里的 "W1" 和 "A16" 分别代表权重矩阵和激活值的量化比特宽度。

"W1" 表示权重矩阵被量化到1-bit。这意味着模型中的权重只使用两个可能的值（通常是-1和+1），这极大地减少了模型的存储需求和计算复杂性。但这种极端的量化会导致信息损失，需要特别的设计和技术来保持模型性能。
"A16" 表示激活值保持16-bit的精度。激活值是神经网络中层与层之间传递的数据，保持16比特的精度有助于减少量化引入的误差，并帮助模型保持一定的计算精度。

2.4 量化工作流程

我们在前面介绍了校准。实际上，在实践中将浮点模型转为量化模型的方法有以下三种方法：

data free：不使用校准集，传统的方法直接将浮点参数转化成量化数，使用上非常简单，但是一般会带来很大的精度损失，但是高通最新的论文 DFQ 不使用校准集也得到了很高的精度。
calibration：基于校准集方案，通过输入少量真实数据进行统计分析。
finetune：基于训练 finetune 的方案，将量化误差在训练时仿真建模，调整权重使其更适合量化。好处是能带来更大的精度提升，缺点是要修改模型训练代码，开发周期较长。

按量化工作阶段的不同（压缩模型的阶段或者说量化应用的时间）来分类，校准可以分为如下三种：

训练中量化（QAT, Quantization-Aware-Training）。QAT 在模型训练过程中加入伪量化算子，让量化目标无缝地集成到模型的训练过程中，然后使用训练数据进行微调，让模型在量化值的约束下进行调整和学习，通过训练时统计输入输出的数据范围来提升量化后模型的精度，适用于对模型精度要求较高的场景。
训练后量化（PTQ, Post-Training-Quantization）。PTQ 在模型训练完成后对其参数进行量化，只需要少量校准数据进行校准，以计算裁剪范围和缩放因子。PTQ的主要优势在于其简单性和高效性，无需对LLM架构进行修改或进行重新训练。适用于追求高易用性和缺乏训练资源的场景。但PTQ可能会在量化过程中引入一定程度的精度损失。
量化感知微调（Quantization-Aware Fine-tuning，QAF）。QAF 在预训练模型的微调期间应用量化。主要目标是确保经过微调的LLM在量化为较低位宽后仍保持性能。通过将量化感知整合到微调中，以在模型压缩和保持性能之间取得平衡。

因为QAF比较小众，所以我们重点介绍QAT和PTQ。

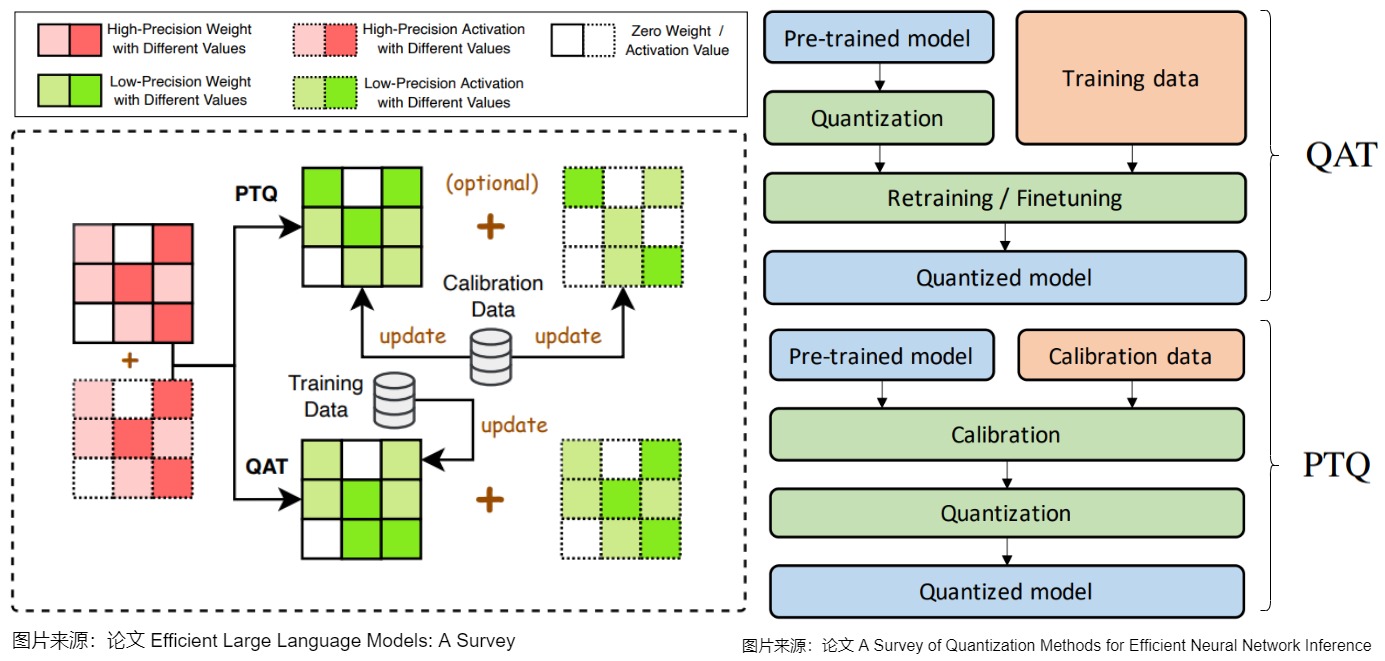
下图是QAT和PTQ之间的比较。在 QAT 中，对预训练模型进行量化，然后使用训练数据进行微调，以调整参数并恢复准确性下降。在 PTQ 中，使用校准数据（例如，训练数据的一个小子集）来校准预训练模型，以计算裁剪范围和缩放因子。然后，根据校准结果对模型进行量化。本质上 PTQ 就是在校准过程中，研究不同的metric来更好地选择截断上下界。

在实际应用中，更为常用的是PTQ的方法，大部分芯片厂商自己的编译器，已经集成了基础的PTQ方法，并与算子融合图优化等组合使用，对绝大部分模型能获得精度与速度都令人满意的结果。PTQ 还有一个额外的优点，那就是它可以应用于数据有限或未标记的情况。然而，与 QAT 相比，这通常会以较低的精度为代价，特别是对于低精度量化。另外，PTQ还有一个缺点是，量化并不考虑实际的训练过程。

2.4.1 PTQ

PTQ涉及在训练模型之后对模型的参数（包括权重和激活）进行量化。

权重的量化可以在推理之前使用对称量化或非对称量化来执行，因为在大多数情况下，在推理期间参数是固定的，裁剪范围可以事先静态确认。但是，激活的量化需要推断模型以获取它们的潜在分布，因为每个输入样本的激活映射是不同的，我们事先不知道它们的范围。

所以这里又引出了激活量化的两种形式，即按照是否推理时使用可以分为静态/动态量化。静态量化是在推理前预先计算量化参数，通过校准样本输入离线找到典型的激活统计信息。动态量化是在运行时使用统计信息来动态计算量化参数，通常更准确但需要较高的开销来计算所需的统计信息。

从架构设计的角度来看，静态量化通过预计算的方式实现了最优的推理性能，这种方案在延迟稳定性和资源效率方面表现出色，特别适合边缘计算和大规模服务器部署场景。而动态量化则通过运行时自适应机制提供了更大的灵活性，能够更好地处理数据分布变化剧烈的场景，这在自然语言处理等领域具有独特优势。

动态量化

动态量化是一种在模型运行时进行量化的技术。它只对权重进行预先量化，对于激活值，则是在运行时动态计算量化参数，即在运行的时候动态计算每个激活的范围。具体流程是：

数据通过隐藏层后，其激活值被收集。
然后使用这些激活值的分布来计算量化输出所需的零点（z ）和比例因子（s）值。
每次数据通过新层时都会重复此过程。每一层都有其自己的z 和 s 值，因此具有不同的量化方案。

动态量化每次计算范围开销很大，不如静态量化快，而且在某些硬件上也没法使用。但是这种方式简单灵活且效果也很好（精度更高），特别适用于那些输入数据分布变化较大的场景。

静态量化

静态量化是在模型推理之前完成的，因此称为"静态"量化。这种方法就是在量化前预先计算激活的范围值（z和s），为了找到这些值，需要使用一个代表性数据（校准数据集），将其提供给模型以收集激活值的分布情况。实际操作步骤如下：

模型训练完成后，在激活函数上放置观察器来记录激活值。
使用校准数据集进行若干次前向传播（大约使用几百个样本就足够了），执行推理流程后统计每层激活值的数据分布并且得到相应的量化参数。
在收集了这些值之后，就可以计算推理过程中执行量化所需的s 和 z 值，然后作为参数的一部分存储下来。
在进行实际推理时，s 和 z 值不会重新计算，而是全局使用，量化所有激活。因为它在校准过程中只用了一组和值。如果在实际推理时激活值的分布变化很大，就可能导致更高的量化误差。

小结

通常，动态量化由于仅尝试计算每个隐藏层的s 和 z 值，因此可能更准确。但是这会大大增加计算时间，因为需要计算这些值。静态量化的精度虽然较低，但由于已经知道用于量化的s 和 z 值，因此速度更快，所以一般都会使用静态量化。

2.4.2 QAT

有时候，一个训练好的模型数值分布较差，各种PTQ策略都不能获得很好的效果的时候，就需要采用QAT的方法，在训练或微调中引入量化误差，约束数值分布从而获得较好的量化结果。或者在少部分特殊的模型结构场景，更低bit量化的量化需求情况下，就得求助于QAT方法。

与训练后量化（PTQ）在模型训练完成之后进行量化不同，QAT是在训练过程中学习量化过程（模拟量化），其利用伪量化算子将量化带来的精度损失计入训练误差，使得优化器能在训练过程中尽量减少量化误差，得到更高的模型精度。

QAT通常比PTQ更精确，因为量化过程已在训练中被考虑。其工作原理如下：

初始化：设置权重和激活值的范围\(q_{min}\)和\(q_{max}\)的初始值；
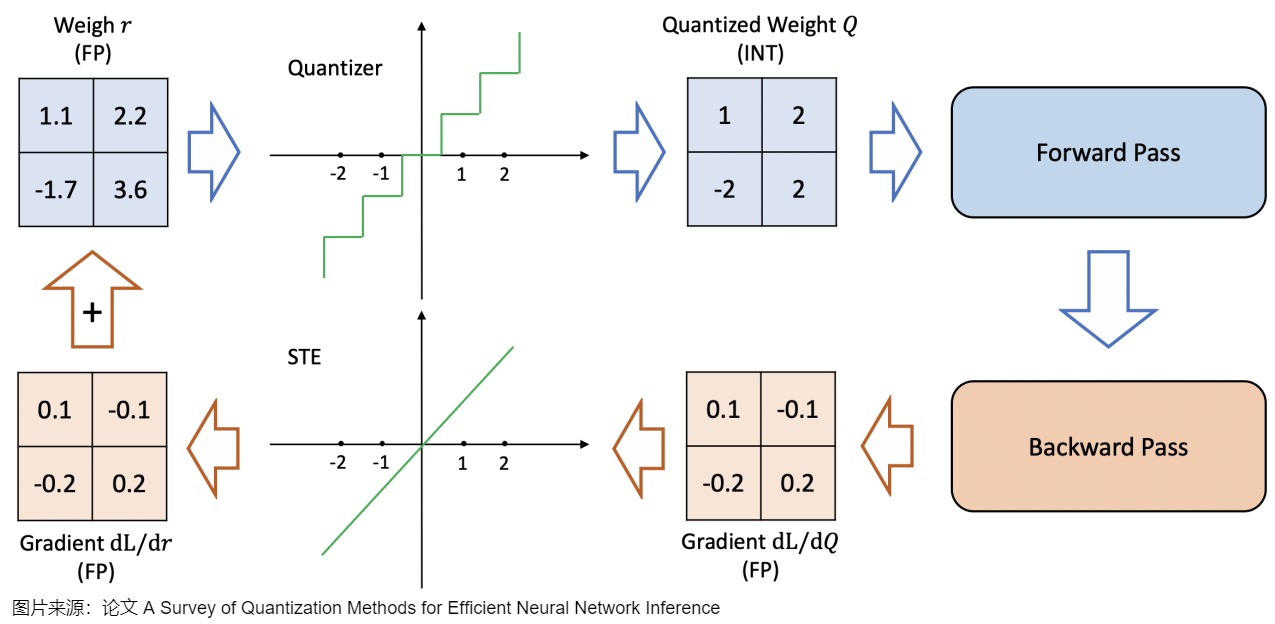
构建模拟量化网络：在需要量化的权重和激活值后插入伪量化算子；这是一个首先将权重量化为例如INT4，然后再反量化回FP32的过程。这个过程允许模型在训练、损失计算和权重更新过程中考虑量化过程。QAT试图探索损失中的"宽 "极小值以最小化量化误差，因为"窄 "极小值往往会导致较大的量化误差。在一个"宽"极小值中选择一个不同的更新权重，其量化误差将大大降低。
量化训练：重复执行以下步骤直到网络收敛，计算量化网络层的权重和激活值的范围\(q_{min}\)和\(q_{max}\)，并根据该范围将量化损失带入到前向推理和后向参数更新的过程中；
导出量化网络：获取\(q_{min}\)和\(q_{max}\)，并计算量化参数s和z；将量化参数代入量化公式中，转换网络中的权重为量化整数值；删除伪量化算子，在量化网络层前后分别插入量化和反量化算子。

所以尽管PTQ在高精度（例如FP32）中有更低的损失，但QAT在低精度（例如INT4）中会获得更低的损失。

2.4.3 推荐流程

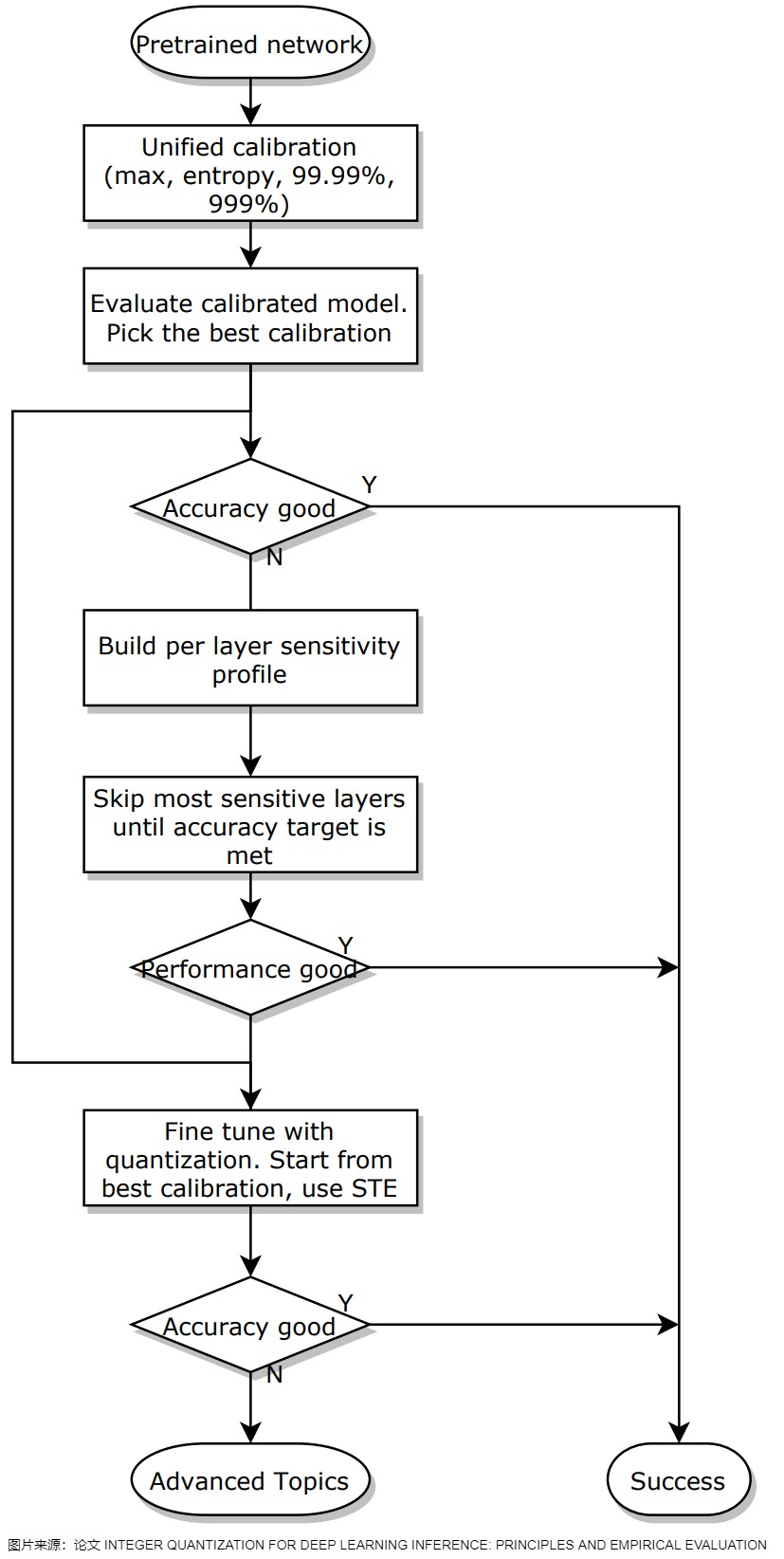
论文"INTEGER QUANTIZATION FOR DEEP LEARNING INFERENCE: PRINCIPLES AND EMPIRICAL EVALUATION"给出了一个推荐的量化工作流，具体参见下面图。

2.5 加速原因

量化模型如何实现加速？其原因大约为以下几个方面：访存加速、向量化运算加速、量化算子优化。

2.5.1 访存加速

量化模型的显存占用与量化bit数呈倍性关系（忽略量化参数的额外显存），这一点对于访存瓶颈的模型来说有极大的好处。现代的高性能运算芯片，对于乘加等并行计算有很强的优化，内存的读写反而成为了瓶颈。通过量化操作将浮点模型转换为低bit，可以显著地降低访存耗时。需要注意的是，某些方案中，量化只针对权重，所以在实际推理时，还需要执行反量化操作获得浮点的权重，再进行计算，所以只看计算量反而是有所增加的。但凭借访存部分的速度提升，便能获得可观的模型整体推理加速。这里其实也体现了模型量化的另一个显著优势点：节省显存。

2.5.2 向量化运算加速

在高性能CPU或GPU tensor core中，为了大规模运算，一般都会设计高效的向量化运算指令来实现并行计算。当向量化运算与模型量化相配合会有很好的效果。举个例子，一个512-bit寄存器，可以同时处理16个32-bit的float数，如果将其量化为8-bit定点数，则同样的资源可以同时处理64个数。

2.5.3 量化算子优化

我们以Cutlass 的FPA_INTB GEMM算子为例来学习。该算子实现了高效的LLM weight-only 量化，被广泛使用。常见的GEMM算子，都是同等精度的tensor进行矩阵乘法，但在大模型量化领域，受限于量化模型精度，weight-only的量化反而更加常见。这就带来一个问题，如何实现量化后的INT4/8 类型权重与float类型的激活之间的GEMM计算。Cutlass 将DeQuant操作与GEMM操作融合进一个算子，同时设计了高效的位操作DeQuant实现，能够实现 26x 的throughput 加速。具体可以参考论文 Who Says Elephants Can't Run: Bringing Large Scale MoE Models into Cloud Scale Production .

0xFF 参考

NeurIPS 2024 Oral：用 DuQuant 实现 SOTA 4bit 量化青稞

压缩神经网络的艺术： MIT 韩松教授的两篇经典论文解析 Yixin

从Training Dynamics到Outlier------LLM模型训练过程中的数值特性分析 Reiase

【读点论文】A Survey of Quantization Methods for Efficient Neural Network Inference 羞儿

A Survey of Quantization Methods for Efficient Neural Network Inference

https://www.armcvai.cn/2023-03-05/model-quantization.html

模型量化技术综述：揭示大型语言模型压缩的前沿技术 [DeepHub IMBA](javascript:void(0)😉

大模型性能优化（一）：量化从半精度开始讲，弄懂fp32、fp16、bf16

便捷的post training quantization方案: GPTQ

【AI不惑境】模型量化技术原理及其发展现状和展望龙鹏-笔名言有三

AWQ, Activation-aware Weight Quantization

大模型量化感知训练开山之作：LLM-QAT 吃果冻不吐果冻皮

ZeroQuant系列(v1, v2)

LLM-QAT: Data-Free Quantization Aware Training for Large Language Models

https://link.zhihu.com/?target=https%3A//github.com/facebookresearch/LLM-QAT)

关于大模型推理的量化算法总结孙培钦

、王文广万字长文揭秘大模型量化的GPTQ方法：从OBS经OBQ到GPTQ，海森矩阵的魔力

王文广万字长文揭秘大模型量化技术：探究原理，理解大模型高效推理最重要的技术

akaihaoshuai：从0开始实现LLM：6、模型量化理论+代码实战（LLM-QAT/GPTQ/BitNet 1.58Bits/OneBit）
akaihaoshuai：从0开始实现LLM：6.1、模型量化（AWQ/SqueezeLLM/Marlin）

https://zhuanlan.zhihu.com/p/703513611

AI大模型高效推理的技术综述！花哥 [AI大模型前沿](javascript:void(0)😉

Zirui Liu, Jiayi Yuan, Hongye Jin, Shaochen Zhong, Zhaozhuo Xu, Braverman, V., Beidi Chen, & Hu, X. (2023). KIVI : Plug-and-play 2bit KV Cache Quantization with Streaming Asymmetric Quantization.

Databricks 博文: LLM Inference Performance Engineering: Best Practices

Coleman Hooper, Sehoon Kim, Hiva Mohammadzadeh, Michael W. Mahoney, Yakun Sophia Shao, Kurt Keutzer, & Amir Gholami. (2024). KVQuant: Towards 10 Million Context Length LLM Inference with KV Cache Quantization.

T. Dettmers, M. Lewis, Y. Belkada, and L. Zettlemoyer, (2022). LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale.

A. Gholami, S. Kim, Z. Dong, Z. Yao, M. W. Mahoney, and K. Keutzer, (2021). A Survey of Quantization Methods for Efficient Neural Network Inference.

KIVI: A Tuning-Free Asymmetric 2bit Quantization for kv Cache :https://arxiv.org/abs/2402.02750

Xiao, Guangxuan, et al. "Smoothquant: Accurate and efficient post-training quantization for large language models." International Conference on Machine Learning. PMLR, 2023.