探秘Transformer系列之（36）--- 大模型量化方案

[探秘Transformer系列之（36）--- 大模型量化方案](#探秘Transformer系列之（36）--- 大模型量化方案)
- [0x00 概述](#0x00 概述)
- [0x01 8位量化](#0x01 8位量化)
  - [1.1 LLM.int8()](#1.1 LLM.int8())
    - [1.1.1 动机](#1.1.1 动机)
    - [1.1.2 方案](#1.1.2 方案)
      - 8位数据类型和量化
      - [逐向量量化（vector-wise quantization）](#逐向量量化（vector-wise quantization）)
      - [混合精度分解（mixed precision decomposition）](#混合精度分解（mixed precision decomposition）)
    - [1.1.3 缺点](#1.1.3 缺点)
  - [1.2 ZeroQuant](#1.2 ZeroQuant)
    - [1.2.1 主要贡献](#1.2.1 主要贡献)
    - [1.2.2 方案](#1.2.2 方案)
  - [1.3 SmoothQuant](#1.3 SmoothQuant)
    - [1.3.1 动机](#1.3.1 动机)
      - 现状
      - 量化方案的问题
    - [1.3.2 方案](#1.3.2 方案)
    - [1.3.3 不足](#1.3.3 不足)
- [0x02 4位量化](#0x02 4位量化)
  - [2.1 GPTQ](#2.1 GPTQ)
    - [2.1.1 背景](#2.1.1 背景)
      - 逐层量化
      - OBQ
        
        OBD
        
        OBS
        
        OBQ
    - [2.1.2 GPTQ 方案](#2.1.2 GPTQ 方案)
      - 特色
      - 取消贪心算法
      - [Lazy Batch-Updates](#Lazy Batch-Updates)
      - [Cholesky(乔莱斯基) 分解](#Cholesky(乔莱斯基) 分解)
      - 总体算法
  - [2.2 AWQ](#2.2 AWQ)
    - [2.2.1 动机](#2.2.1 动机)
    - [2.2.2 方案](#2.2.2 方案)
      - 选择权重
      - 激活感知缩放
        
        推导
        
        问题
        
        最优缩放因子搜索
      - 应用
      - [与 SmoothQuant 的关系](#与 SmoothQuant 的关系)
  - [2.3 LLM-QAT](#2.3 LLM-QAT)
    - [2.3.1 动机](#2.3.1 动机)
    - [2.3.2 方案](#2.3.2 方案)
      - [Data-free 蒸馏](#Data-free 蒸馏)
      - 知识蒸馏
      - 量化函数
      - [KV Cache的量化感知训练](#KV Cache的量化感知训练)
      - 结论
  - [2.4 QLoRA](#2.4 QLoRA)
    - [2.4.1 动机](#2.4.1 动机)
    - [2.4.2 方案](#2.4.2 方案)
  - [2.5 FlatQuant](#2.5 FlatQuant)
    - [2.5.1 动机](#2.5.1 动机)
    - [2.5.2 方案](#2.5.2 方案)
- [0x03 低位量化](#0x03 低位量化)
  - [3.1 SqueezeLLM](#3.1 SqueezeLLM)
    - [3.1.1 动机](#3.1.1 动机)
    - [3.1.2 方案](#3.1.2 方案)
      - 基于敏感度的非均匀量化
      - 针对离群点的稠密稀疏量化
  - [3.2 SpQR](#3.2 SpQR)
    - [3.2.1 动机](#3.2.1 动机)
      - 离群值
      - 参数灵敏度分析
    - [3.2.2 方案](#3.2.2 方案)
      - 量化算法
      - 稀疏量化表示的实现和利用
  - [3.3 BitNet](#3.3 BitNet)
    - [3.3.1 方案](#3.3.1 方案)
      - 架构
      - 流程
        
        权重量化
        
        激活量化
        
        反量化
        
        QAT
    - [3.3.2 结果](#3.3.2 结果)
  - [3.4 BitNet b1.58](#3.4 BitNet b1.58)
    - [3.4.1 方案](#3.4.1 方案)
      - 0的力量
      - 量化
  - [3.5 OneBit](#3.5 OneBit)
    - [3.5.1 主要贡献](#3.5.1 主要贡献)
    - [3.5.2 挑战](#3.5.2 挑战)
    - [3.5.3 方案](#3.5.3 方案)
- [0xFF 参考](#0xFF 参考)

0x00 概述

继前一篇介绍了大模型量化基础之后，本篇我们来看看一些量化方案。

因为大家目前都用压缩到某个bit来衡量量化方案，因此我们接下来就按照量化比特来进行分类学习。

0x01 8位量化

因为目前硬件 (例如 NVIDIA GPU、Intel CPU、高通 DSP 等) 普通都支持INT8 GEMM，因此为了加快推理速度，研究人员提出了将 weight 和 activation 量化为 INT8 (即 W8A8)的方案。

下图给出了几种8bit量化方案的对比。

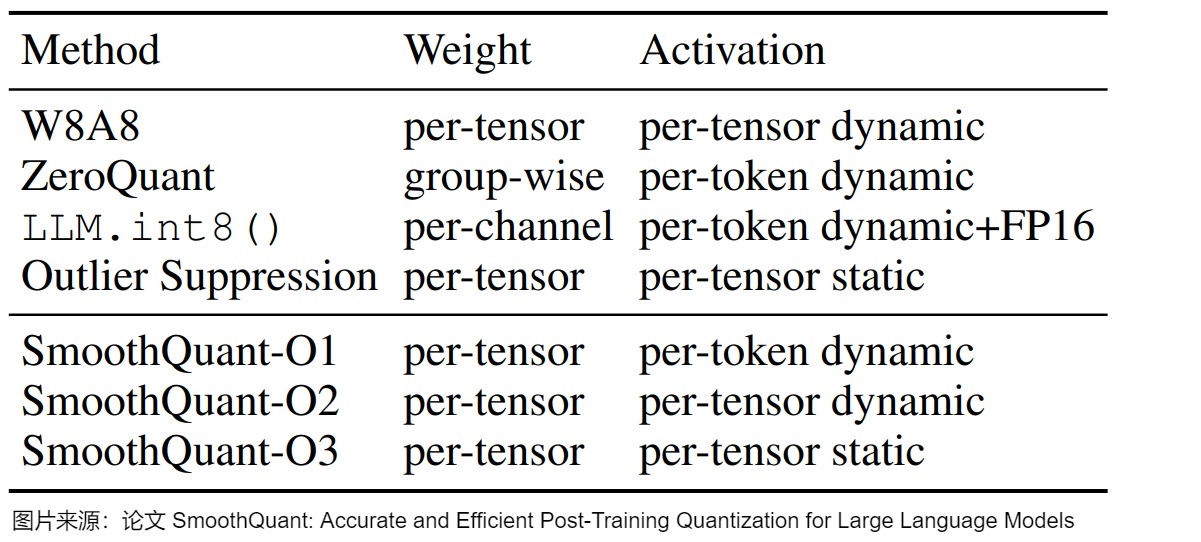
本节介绍的三种方案特点摘要如下。

方法	量化权重与激活	特点
LLM.int8()	W8A8	混合精度量化，离群点保持FP16，其它值量化为INT8
ZeroQuant	W8A8	应用Dynamic per-token activation 量化和分组 weight 量化。
SmoothQuant	W8A8	提出了一种按通道缩放的方法，将高精度量化的复杂性从激活转移到权重，借此平滑激活异常值。

1.1 LLM.int8()

LLM.int8()出自论文" LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale"，是 LLM 量化早期工作之一。论文的核心思想是分而治之。对绝大部分权重（Per-channel）和激活（Per-token）用8bit量化（vector-wise）。对离群特征的几个维度保留16bit，不进行量化。

1.1.1 动机

作者首先提出了activation outlier概念，这是后续大模型量化一直都在注重的点，这两年大模型的优化主要集中在保持activation outlier对应的权重的基础上如何做量化。

LLMs的激活非常难以量化，是因为激活中会出现具有大幅度的activation outlier，导致较大的量化误差和准确性下降。这些离群值与正常值相比会有数百倍的数值差距。activation outlier影响巨大，容易导致量化失败。因为如果按照张量量化的方案，会一个tensor共享一个缩放值，这样，只要有一个异常值就能破坏量化的精度。试想一下，张量的大部分值都在0到1之间，假设有一个异常值等于一万，量化之后，这一个异常值就把其它的值拉到0了，会产生很大的精度损失。但同时又有研究表明，这部分离群值会对模型的性能产生显著影响，因此必须想办法保留离群值而不是直接清零，这就产生了一个难以调和的矛盾。

作者发现激活中的异常值集中在一小部分通道中，且outliers占据的维度很少(不到1%)。于是作者思考，是否可以把异常值单独分出来处理。剩下的部分只使用一个缩放值就可以得到很好的结果了。另外，作者认为，其实换个角度来看，矩阵乘法可以看成是左边矩阵的行和右边矩阵的列在做点乘。如果我们把左边矩阵按行做量化，右边矩阵按列做量化，那么就可以得到更加精确的量化值，可以进一步得到更高的精度。

1.1.2 方案

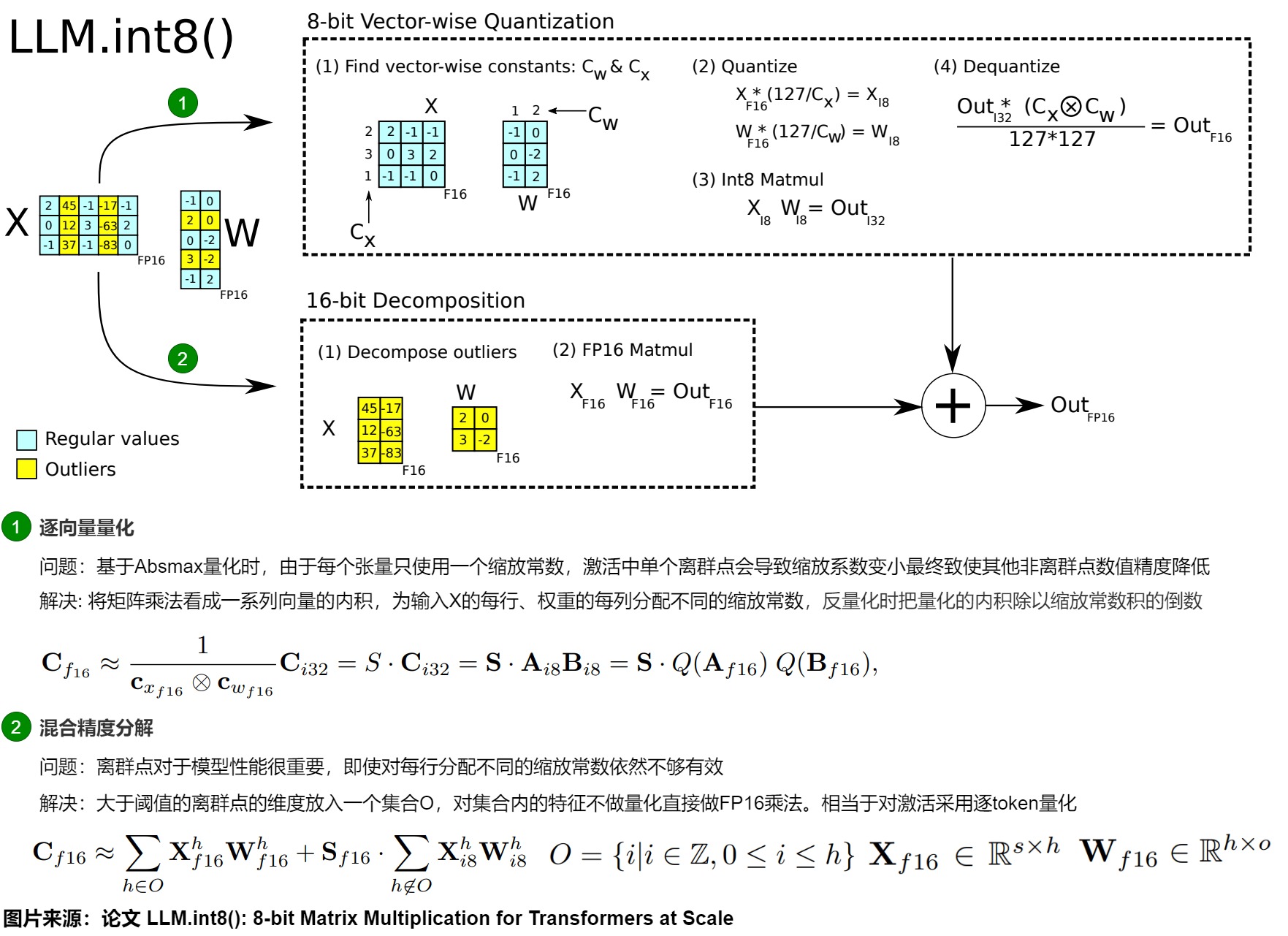
基于以上思考，论文提出了一个两步量化方法 LLM.int8()。

逐向量量化。具体是：
- 从输入的隐含状态中，按列提取异常值 (离群特征，即大于某个阈值的值)。
- 根据输入通道内的离群值分布将激活和权重分成离群值和普通值两个不同的部分。包含激活值和权重的异常数据的通道以FP16格式存储，其他通道则以INT8格式存储。后续会对每个向量内积使用不同的归一化常数。
混合精度矩阵分解。具体是：
- 对绝大部分权重和激活的正常特征仍然用8bit量化（vector-wise）后计算（W8A8），计算完成后再量化为FP16。对离群特征的几个维度保留FP16，对其做高精度的矩阵乘法（W16A16）。
- 把反量化非离群值的矩阵乘结果与离群值矩阵乘结果相加，获得最终的 FP16 结果。

具体如下图所示，通过离群(Outlier)检测，把输入X和权重W中包含异常值的行、列挑选出来直接做fp16的浮点矩阵乘法，然后剩下的正常点（X每一行用absmax进行量化、W每一列用absmax进行量化）量化后进行int8乘法再反量化回fp16，最后把它们累加起来作为最终结果输出。

8位数据类型和量化

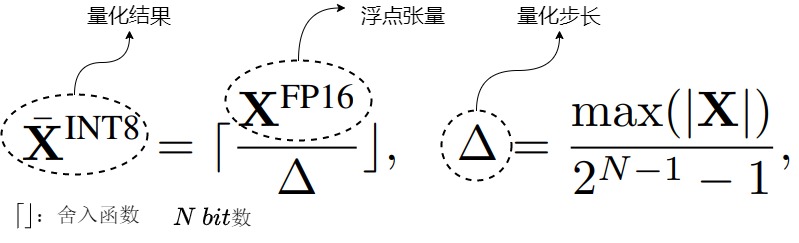
我们首先看看8位数据类型和量化的特点。这里介绍的是高精度非对称量化 (Zeropoint quantization) 和对称量化 (Absmax quantization)。虽然 Zeropoint 量化通过使用数据类型的全位范围来提供高精度，但由于实际的限制，它很少使用。Absmax 量化是最常用的技术。

下图(a)表示Absmax量化，b)表示Zeropoint量化。[β，α]分别表示区间最小和最大值。

Absmax量化：除以绝对值的最大值乘127从而把输入缩放到8位宽 [−127,127] ， ⌊⌉ 表示取最近邻整数，记$s_{xfl16}$为缩放系数。该方法即为缩放量化。
Zeropoint量化：上述量化方案对于ReLU的输出只有正区间被使用，而Zeropoint提出使用动态区间 ndx 缩放，使用零点 zpx 平移，从而可使用全区间数值。该方法即为仿射量化，更准确但由于实际限制该方法较少使用。

逐向量量化（vector-wise quantization）

当进行Absmax量化时，会为每个 tensor 使用一个 scaling 常数。由于每个tensor只使用一个缩放常数，激活中存在单个离群点会导致缩放系数变小，最终致使其他非离群点数值精度降低。如果每个张量有多个 scaling 常数就可以缓解此问题。因此，作者使用了 Vector-wise Quantization。

Vector-wise Quantization具体为：将矩阵乘法看成一系列向量（独立的行与列）的内积，可对每个内积使用不同的归一化常数。对于给定输入 $X_{f16}$和权重 $W_{f16}$，输入为FP16的int8矩阵乘法，我们为输入 $X_{f16} \in R^{s×ℎ}$ 的每行、权重 $W_{f16} \in R^{ℎ×o}$ 的每列分配不同的缩放常数 $c_{xf16}$ 和 $c_{wf16}$ ，反量化时把量化的内积除以缩放常数积的倒数。对于整个矩阵乘法，这相当于外积$c_{xf16}⊗c_{wf16}$的反规范化（denormalization）。并且，可以在下一个操作前，通过反归一化恢复矩阵乘法的输出。

混合精度分解（mixed precision decomposition）

参数规模达到十亿级的 8-bit Transformer 的一个重要问题是，它们具有异常值特征，需要高精度的量化。然而， Vector-wise Quantization（量化隐藏状态的每一行）对异常值特征依然不够有效。作者观察到，这些异常值特征在实践中既非常稀疏又有规律，仅占所有特征维度的 0.1%。因此，作者开发了一种新的矩阵乘法的混合精度分解技术：将大于阈值 $\alpha$ 的离群点的维度放入一个集合O，对集合内的特征不做量化、直接做FP16乘法，而其他维度进行8位乘法。实验发现，当$\alpha$=6.0，就足以抵消量化带来的降级影响（performance degradation）。因为异常值特征维度通常小于7即 |O|≤7 ，因此分解操作基本只消耗很少内存。

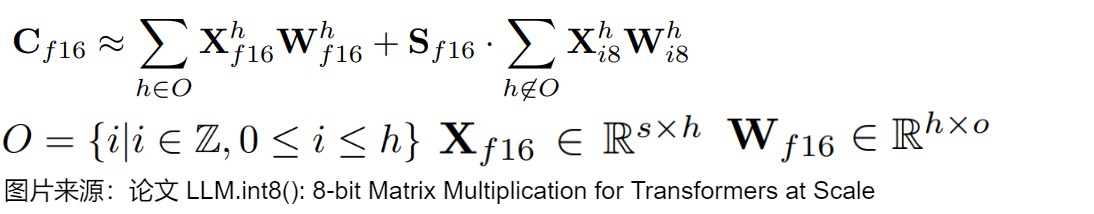
1.1.3 缺点

论文不足点如下：

很难在硬件加速器上高效实现outlier的分解，而且运行时进行异常值检测，这导致推理速度比fp16还慢
模型量化仅到8bit，仍是4bit的2倍大。

1.2 ZeroQuant

1.2.1 主要贡献

ZeroQuant的主要贡献如下：

对激活按 per-token 的动态量化，每个token都有独立的量化参数。对权重矩阵进行分组量化，每组都有独立的量化参数。这样兼顾了性能和精度。
提出一种无需访问原始训练数据的逐层知识蒸馏算法（LKD）来提取量化网络，降低了显存开销。

1.2.2 方案

用于激活的按token量化

现有 PTQ 中对激活进行量化常见做法是静态量化，其中最小/最大范围是在离线校准阶段计算的。

对于激活范围方差较小的小模型来说，这种方法可能就足够了。然而，LLM的激活范围存在巨大差异。因此，静态量化方案（通常应用于所有tokens/样本）将导致准确度显著下降。克服这个问题的一个办法就是采用更细粒度的token-wise量化并动态计算每个token的最小/最大范围，以减少激活引起的量化误差。然而，使用现有的深度学习框架直接应用 token-wise 量化会导致显著的量化和反量化成本，因为 token-wise 量化引入了额外的操作，导致 GPU 计算单元和主存之间产生昂贵的数据移动开销。

为了解决这个问题，ZeroQuant 构建了一个高度优化的推理后端，用于Transformer模型 token-wise 量化。例如，ZeroQuant 的推理后端采用算子融合技术将量化算子与其先前的算子（如Layer Norm）融合，以减轻 token-wise 量化的数据移动成本。类似地，在将最终 FP16 结果写回到下一个 FP16 算子（如：GeLU）的主存之前，使用权重和激活量化 scales 缩放 INT32 accumulation，可以减轻不同 GeMM 输出的反量化成本。

Token-wise 量化可以显著减少量化激活的表示误差，它不需要校准激活范围，对于ZeroQuant 的量化方案（INT8 权重和 INT8 激活）不存在与量化相关的成本（例如，激活范围校准）。

用于权重矩阵的分组量化

将 INT8 PTQ 应用于 BERT/GPT-3 模型会导致准确性显著下降。关键的挑战是 INT8 的表示无法完全捕获权重矩阵中不同行和不同激活Token的不同数值范围。解决这个问题的一种方法是对权重矩阵（激活）使用group-wise（token-wise）量化。

分组量化最先在Q-BERT中提出，其中权重矩阵被划分为 g 个组，每个组单独量化。然而，在Q-BERT中，作者仅将其应用于量化感知训练。更重要的是，他们没有考虑硬件效率约束，也没有系统后端支持，因此没有降低时延。

ZeroQuant 的设计中考虑了 GPU Ampere 架构（例如: A100）的硬件约束，其中计算单元基于 Warp Matrix Multiply and Accumulate (WMMA) 的分片（Tiling）大小，以实现最佳加速。与单矩阵量化相比，ZeroQuant 的分组量化由于其更细粒度的量化而具有更好的精度，同时极大的降低了延迟。

逐层知识蒸馏

知识蒸馏（KD）是缓解模型压缩后精度下降的最有力方法之一。然而，当应用到LLM上时，KD 存在一些局限性：

KD 需要在训练过程中将教师和学生模型放在一起，这大大增加了内存和计算成本；
KD 通常需要对学生模型进行充分训练。因此，需要在内存中存储权重参数的多个副本来更新模型；
KD 通常需要原始训练数据，有时由于隐私/机密问题而无法访问。

为了解决这些限制，ZeroQuant 提出了逐层蒸馏（LKD）算法缓解精度损失。该算法将原始模型作为教师模型，量化后的模型作为学生模型，通过逐层传递知识的方式，引导学生模型模仿教师模型的输出。这种方法不需要原始训练数据，且能够在不增加额外计算成本的情况下，有效提升量化模型的精度。

第二版ZeroQuant-V2分析了权重量化和激活值量化对精度的敏感性，比较了常用PTQ算法的模型效果，最后引入了一种称为低秩补偿（LoRC）的优化技术，它可以与 PTQ 的协同工作，以最小的模型参数大小的增加来改善整个模型质量的恢复，但这种方法的扩展性似乎不是很好。

第三版ZeroQuant-FP主要探索了浮点（FP）量化的可行性，特别关注FP8和FP4格式。对于LLM，FP8激活在性能上优于INT8，而在权重量化方面，FP4在性能上与INT4相比具有可比性，甚至更优越；LoRC有助于提升W4A8的整体表现。同时为了解决由权重和激活之间的差异(从FP4到FP8)引起的挑战，ZeroQuant-FP要求所有缩放因子为2的幂，并将缩放因子限制在单个计算组内。

第四版ZeroQuant-HERO是一种新的硬件增强型训练后 W8A8 量化框架，它考虑了内存带宽限制和计算密集型运算，总体偏工程方向，将transformer中更多子模块进行了量化改造，分别是：Embedding层量化、Attention模块量化、MLP 模块量化，同时采用不同量化精度对各个模块进行量化组合，按需选取量化等级。

1.3 SmoothQuant

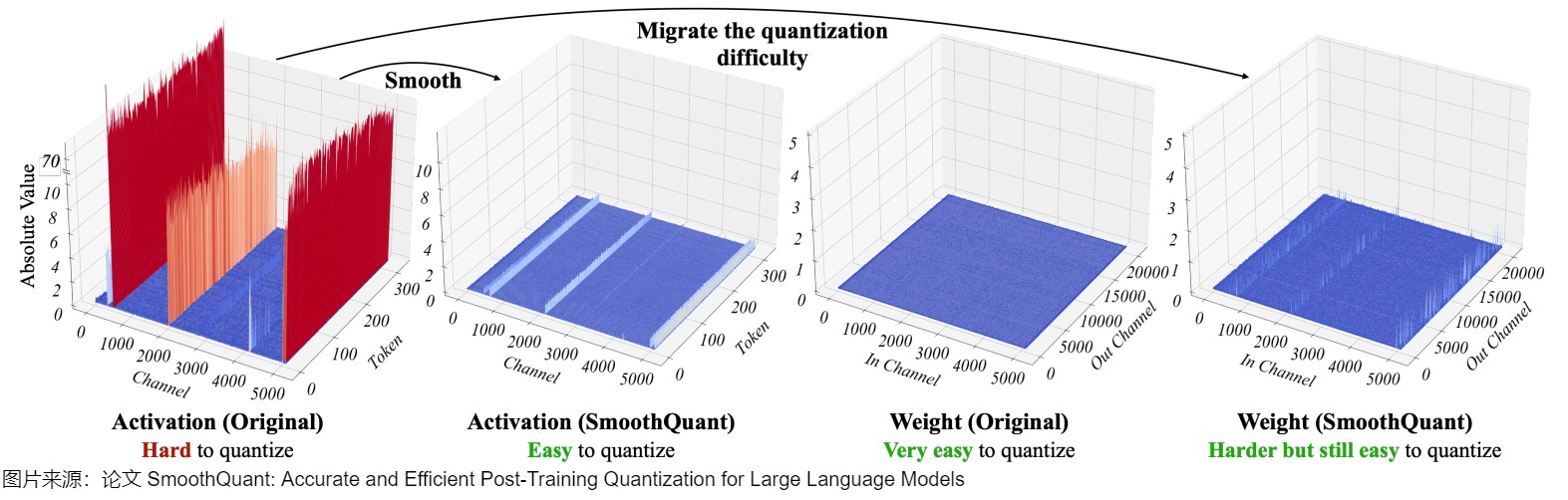
SmoothQuant由论文"SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models"给出，其量化位宽为 W8A8，即权重和激活都是用 8bit 量化。

SmoothQuant 的核心思路是，激活 X 之所以难以量化，是因为存在离群值拉伸了量化的线性映射范围，导致大部分数值的有效位数减少。而且，不同token在激活通道之间具有相似变化。因此，论文提出了一种按通道缩放的方法，在离线阶段引入平滑因子 s 来平滑激活中的异常值，并通过数学上的等效转换将量化的难度从激活迁移至权重 W 上（逐通道对权重乘上缩放因子，在激活上乘上缩放因子矩阵的逆，从而保持整体的输出不变，激活值整体变小，权重整体变大，激活值更好量化了），从而降低激活的量化难度。经过平滑处理的激活 X 和调整后的权重 W 均易于量化。

1.3.1 动机

现状

针对异常值，ZeroQuant 和 LLM.int8() 提出了各自的解决办法：

ZeroQuant 应用了动态逐 token 激活量化和分组权重量化来解决激活离群值问题。虽然该方法实现效率较高，但对于 175B 参数的 OPT 模型的准确性较差。
LLM.int8() 通过引入混合精度分解（即对异常值保持 FP16，其他激活使用 INT8）解决了该准确性问题，但是这种方法在工程上很难在 AI 加速器上高效实现，是一种硬件不友好的量化方案。

因此，需要寻找到一种高效、对硬件友好且无需训练的量化方案，使得 LLMs 中所有计算密集型操作均采用 INT8。

量化方案的问题

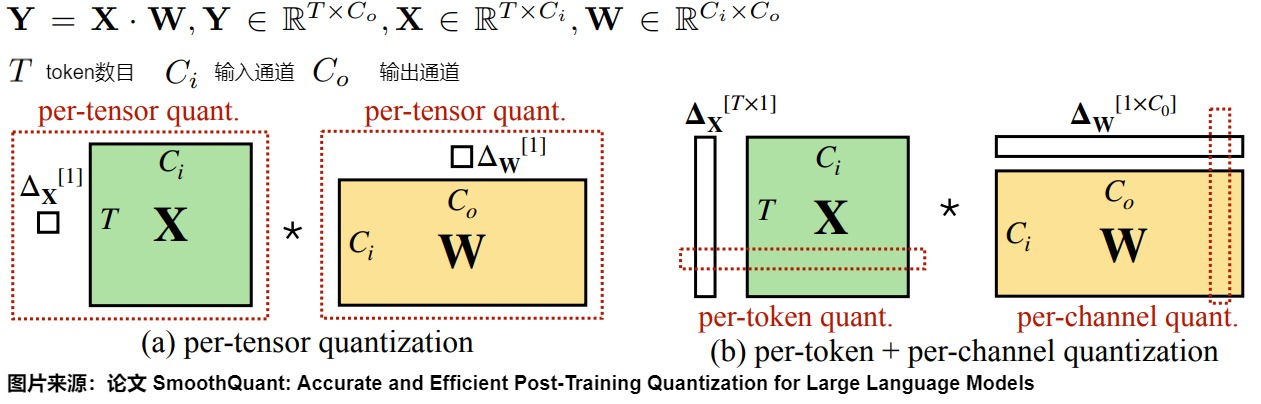
根据量化参数 s（数据量化的间隔）和 z（数据偏移的偏置）的共享范围，即量化粒度的不同，量化方法也可以分为逐层量化（per-tensor）、逐通道（per-channel）量化，逐token（per-token）量化和逐组量化（per-group，Group-wise）。SmoothQuant 作者对比了这几种量化方案，得出结论如下：

per-tensor量化是在硬件上最高效的实现方式。
per-channel量化保留了精度，但是它与 INT8 GEMM 内核不兼容（要求权重和激活都是INT8）。即per-channel量化不能很好地映射到硬件加速的GEMM内核（硬件不能高效执行，从而增加了计算时间）。在这些内核中，缩放只能沿着矩阵乘法的外部维度执行 (即激活的 token 维度、权重 $𝐶_𝑜$ 的输出通道维度)，不能在内部维度$C_i$进行。具体参见下图。
因此，尽管 per-token 量化精度较低，为了不降低GEMM 内核本身的吞吐量，过往的研究依然还是在线性层中采用了它。但是它们无法解决 activation 量化的问题。

因为就离群值来说，不同 tokens 在其通道上表现出类似的变化，于是 SmoothQuant 提出了一种数学上等价的逐通道缩放变换（per-channel scaling transformation）方案，可显著平滑通道间的幅度，从而使模型易于量化，保持精度的同时，还能够保证推理提升推理速度。

我们再来梳理下为何per-channel量化不能很好地映射到硬件加速的GEMM内核。其根本原因是：如果不考虑加速的话，只是为了压缩参数，那么怎么量化都行。如果想加速矩阵乘法，就要考虑整个矩阵乘法的反量化。只能在矩阵乘法的外侧维度进行量化，否则无法反量化。

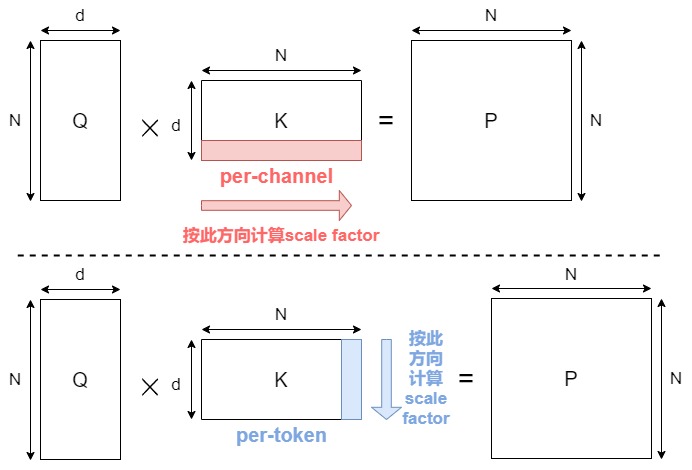
我们以注意力机制量化为例来继续分析。假如对K 做 channel-wise 量化，是可以避免不同 channel 之间的值共享scale factor。然而这在注意力机制计算中会有问题。这是因为在进行矩阵乘法 $QK^T$ 后，得到的结果矩阵的维度是 N × N。如果我们对 K 进行了per-channel 量化（上图上方，总共 d 个channel，每个 channel 包含 N 个元素），每个通道都有一个独立的scale factor，总共是 d 个 scale factor。在反量化（dequantization）时，我们需要将量化后的结果乘以对应的scale factor，而$QK^T$ 的结果矩阵的维度是 NxN，没有 d 的通道维度直接对应，无法使用 K 的通道维度的缩放因子进行正确的反量化。因此，注意力乘法中，对于每个矩阵，我们只能沿着公共维度进行量化（如上图下方）。根据这个简单的原则，Attention 中四个矩阵可以量化的组合如下。

	Q	K	P	V
per-channel	N	N	N	Y
per-token	Y	Y	Y	N
per-block	Y	Y	Y	N

1.3.2 方案

SmoothQuant提出了8bit weight，8bit activation(W8A8)的量化方法，此方案其实可以看做数据的预处理，处理完之后的数据可以适配int8量化方法。主要思路就是，由于权重很容易量化，而激活则较难量化，因此将量化难度从激活迁移到下一层的权重内，利用weight的细粒度量化来承担该量化困难。方案特点如下：

引入平滑因子s来平滑激活异常值，将量化难度从激活等价转移到权重上；
平滑因子的作用是建立一个数学上等效的变换，即将input的动态范围除上scale（该scale > 1）即可以实现动态范围减小，从而改善量化结果，然后将该scale吸到下一层的weight内；
利用weight的细粒度量化来承担该权重的量化困难（因为input往往使用token-wise quantization，而weight通常使用channel-wise quantization或group-wise quantization）；

SmoothQuant 算法有两个难点：如何通过数学上的等效转换将量化的难度从激活迁移至权重上，以及如何实现逐通道的等效缩放转换。这具体是通过矩阵乘法升级和合理计算平滑因子来达到目的。

计算平滑因子

SmoothQuant 的目标是为每个 channel 选择一个平滑因子 𝑠 ，使得 $\hat X=𝑋diag(𝑠)^{−1}$ 易于量化。为了减少量化误差，应该增加所有通道的有效量化位。当所有 channel 都具有相同的最大幅值时，总有效量化位将是最大的。

一种做法是让 $s_j = max(|X_j|),j=1,2,...,C_j$， $C_j$代表第 j 个 input channel。各 channel 通过除以 $s_j$后，激活 channels 都将有相同的最大值，这时激活比较容易量化。但是这会使得激活值的离群值全部转移到权重上面，激活值变得很好量化，权重反而难以量化。
另一种做法是让$s_j=1/max(|W_j|)$，这样权重 channels 都将有相同的最大值，权重易量化。即将所有量化难度从权重迁移到激活，这会使得原本方差较小的权重方差更小，激活值方差更大，更难以量化激活。

因此，我们需要在 weight 和 activation 中平衡量化难度，让彼此均容易被量化。论文作者通过加入一个超参 $\alpha$ （迁移强度），来控制从激活值迁移多少难度到权重值。一个合适的迁移强度值能够让权重和激活都易于量化。$\alpha$ 太大，权重难以量化，$\alpha$ 太小，则激活难以量化。下图中。

$\alpha$ 表示迁移强度，为一个超参数，控制将多少激活值的量化难度迁移到权重量化。
C 表示激活的输入通道数。

对于缩放系数，其实可以离线使用一个小的标定数据集进行计算，考虑到 X一般都是从前一个线性操作得到的，我们事实上可以把对X的scale融合到前一个线性层。而对于weight的量化，也可以在计算好当前层的缩放系数(以及下一层X的缩放系数)后乘起来再做量化。这样就可以避免在推理的时间计算缩放矩阵的乘法。

矩阵乘法升级

有了平滑因子，就可以实现离群值平滑了，其本质上是通过将激活难度转移至权重来实现的。

常规的矩阵乘为$Y=XW$。SmoothQuant 通过按通道除以 smoothing factor 来对激活进行平滑。即为了保持线矩阵乘法在数学上的等价性，以相反的方式对权重进行对应调整。X 在 channel 维度（列）上每个元素除以 $s_i$ ，W则在每行上每个元素乘以 $s_i$ 。这样 Y 在数学上是完全相等的。

具体转换过程如下图。

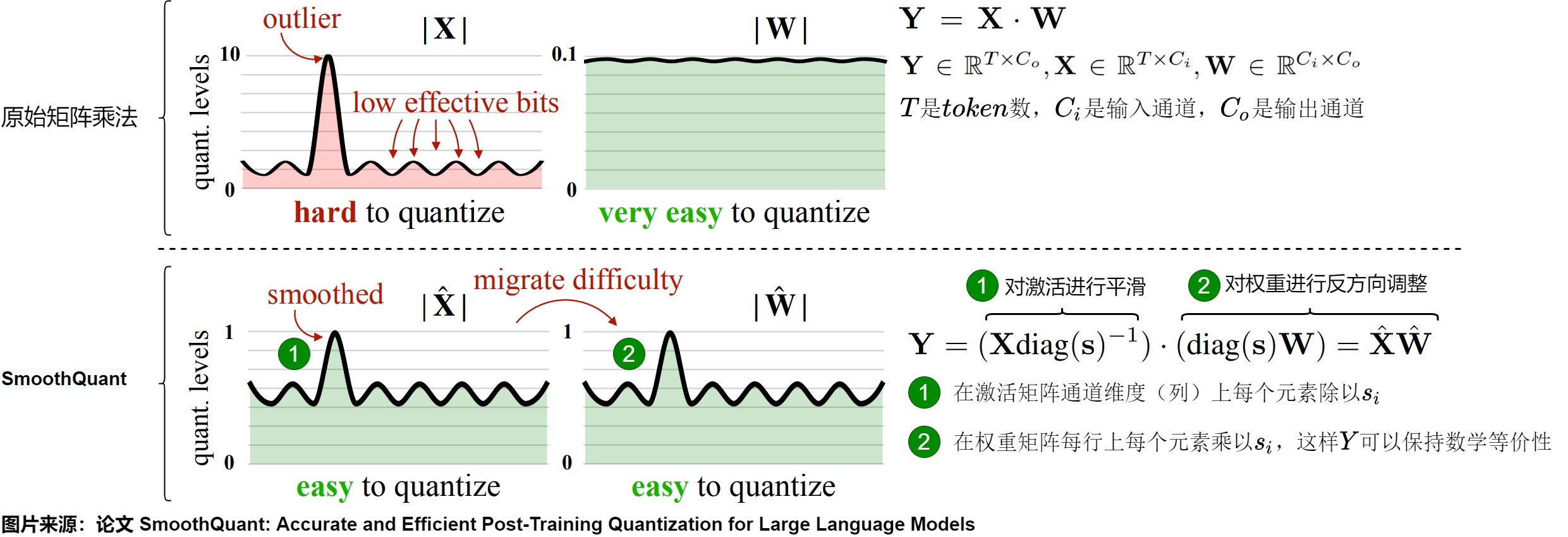
考虑到输入 X 通常由前面的线性操作（如线性层、层归一化等）产生，我们可以轻松地将平滑因子离线地融合到前一层的参数中$diag(s) \times W_{pre}$，不会因额外的缩放操作而导致增加内核调用开销。在一些其他情况下，例如当输入来自残差相加时，我们可以在残差分支中添加额外的缩放。

示例

下图给出了计算流程。其中，平滑因子 s 是离线在校准样本上获得的。

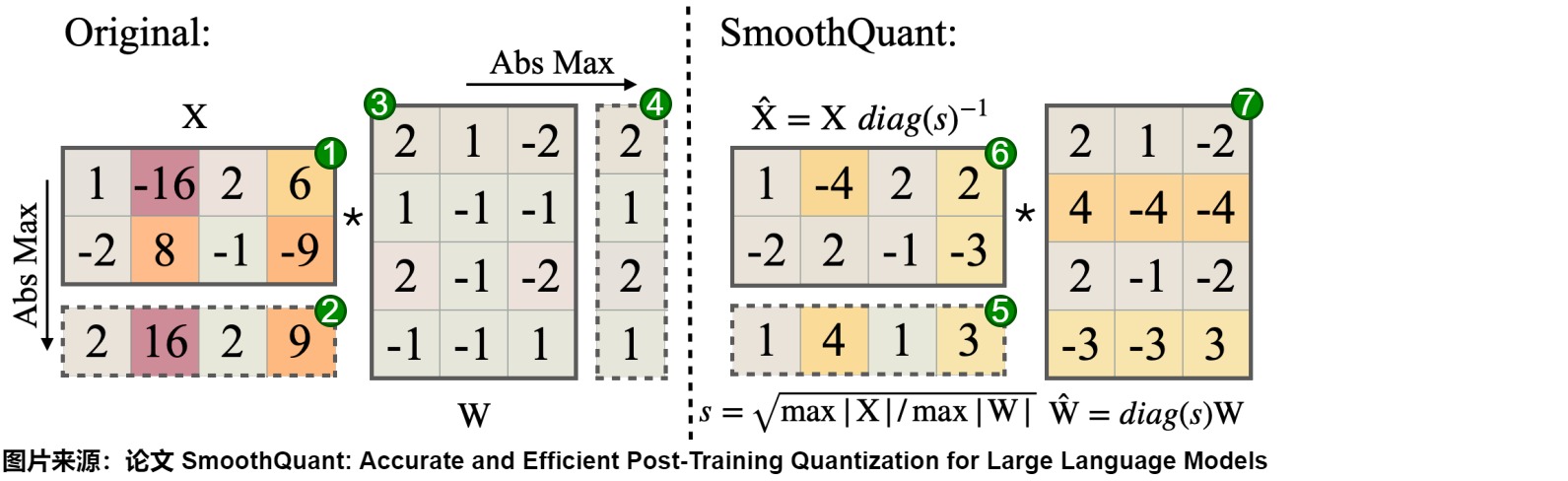
具体步骤如下图，其中，图上的红色标号b，d，d是离线校准阶段。e和f是平滑阶段，e是推理阶段。

准备阶段
- X是标号1，W是标号3。
校准阶段（离线）
- X按照列计算，得每列元素绝对值的最大值，即标号2。
- W按照行计算，得每行元素绝对值的最大值，即4号。
- 标号2和标号4进行运算，即按照公式s进行运算，得到标号5。
平滑阶段（离线）
- 1号除以5号，得到6号。 $\\hat{W}$ 的计算公式如下：$\hat{W}=diag(s)$
- 3号乘以以5号，得到7号。$\hat{X}$的计算公式如下：$\hat{X}=X diag(s)^{-1}$
推理阶段（在线，部署模型）
- 6号乘以以7号，得到Y。平滑之后的激活的计算公式如下：$Y = \hat{X} \hat{W}$

应用

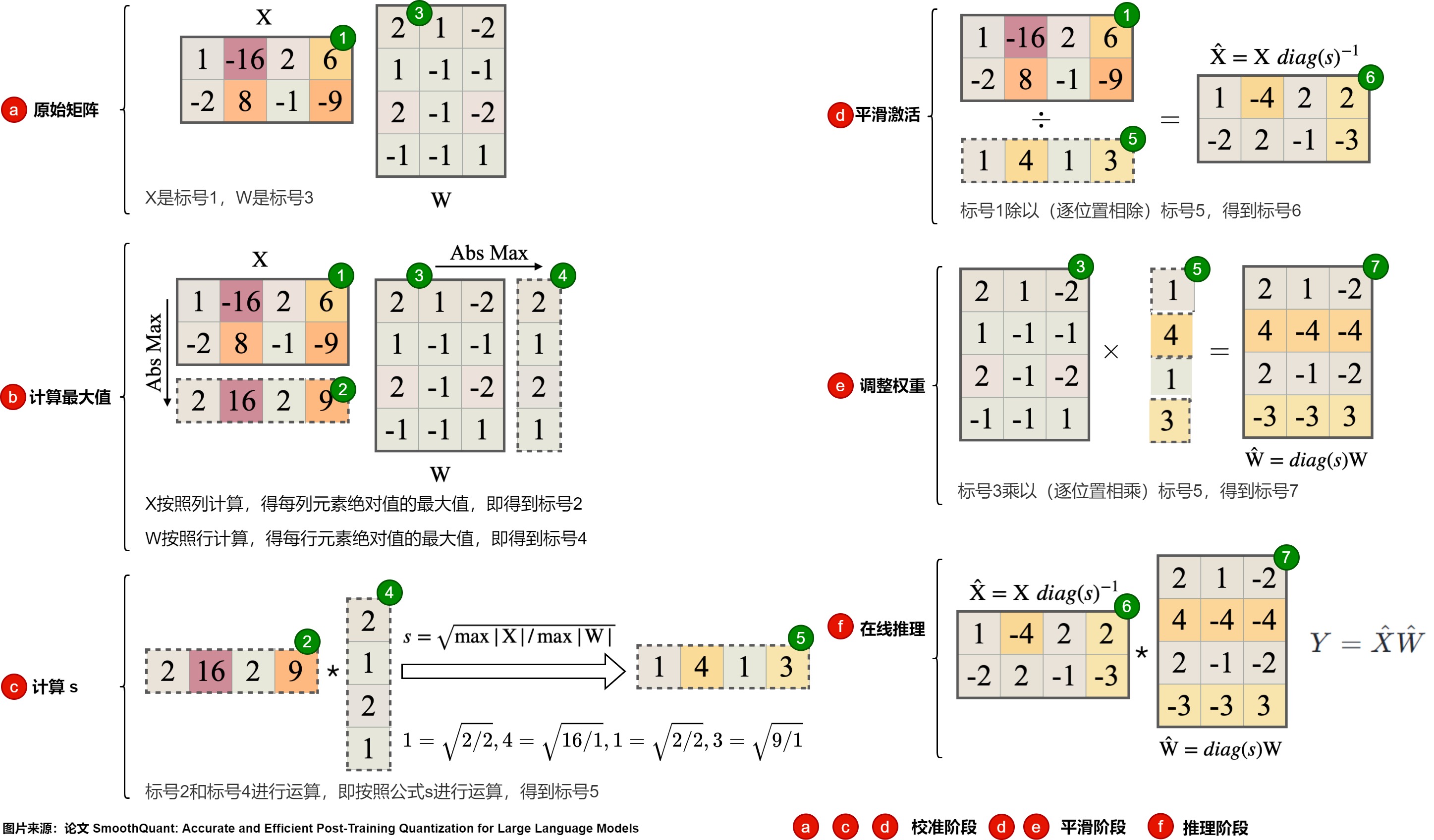
因为线性层占据了大型语言模型中大部分的参数量和计算开销。默认情况下，作者对自注意力和前馈层的输入激活进行平滑处理，并将所有线性层量化为 W8A8。同时，作者也对注意力机制中的 BMM 操作进行量化。下图展示了作者针对 Transformer 模块设计的量化流程：

对线性层和注意层的 BMM（批量矩阵乘法）等计算量大的算子的输入和权重进行INT8量化（W8A8）。
对于 Softmax 和 LayerNorm 等其他轻量级逐元素（element-wise）操作模块，则保持激活为 FP16。

这样设计有助于平衡准确性和推理效率。不量化 Token Embedding 层的原因，可能是因为其参数冗余性较小且不存在权重稀疏现象。

1.3.3 不足

SmoothQuant 不足点如下：

适用于LLM，在stable diffusion上表现欠佳；

使用小批量数据离线进行标定，有过拟合标定数据的风险。
精度没有LLM.int8()有保证, 且容易受到calibration-set的影响), 同时一旦weight精度调至4bit, 则模型精度下滑严重)

0x02 4位量化

当LLM参数变大时，上述提到的INT8量化方案在低比特位精度下会存在显著的性能劣化。例如，SmoothQuant在 W4A4、W3A4、W2A16 和 W2A8 等低比特位设置下表现出较大的精度下降，从而影响了量化模型的实际使用体验。因此，需要更低比特位的方案，比如GPTQ和AWQ提出的4比特方案。

GPTQ和AWQ成功地将LLMs的权重矩阵压缩到4bit，同时保持了LLMs的主要能力。这代表了LLM优化的重大进展，通过在时间和空间效率以及模型性能之间实现平衡。论文"The case for 4-bit precision: k-bit inference scaling laws"深入探讨了LLM中模型大小和比特精度之间在零样本性能方面的权衡。他们在各种LLM家族之间进行了广泛的实验，在全部的模型比特数和零样本准确性之间，发现4比特精度几乎普遍是实现平衡的最佳选择。

本节介绍的几种方案特点如下。

方法	量化权重与激活	特点
GPTQ	W3A16, W4A16	根据海森矩阵顺序量化一列权重并调整未量化的权重补偿损失，提出顺序并行量化、延迟更新和Cholesky分解加速。
AWQ	W4A16	Weight：Per-group，Activation：FP16。根据激活幅值选择重要权重并单独缩放这些权重和激活，通过网格搜索最优缩放因子。
LLM-QAT	W4A16	大模型量化感知训练的开山之作。除了量化权重和激活之外，还量化了 KV 缓存，这对于提高吞吐量和支持当前模型规模的长序列依赖至关重要。
QLoRA	W4A16	将低秩自适应与量化相结合，以实现大型模型的有效微调，同时最大限度地降低计算成本和内存使用。
FlatQuant	W4A4	探索平坦分布与量化损失的优化路径

2.1 GPTQ

GPTQ出自论文"GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers"，其思路是通过二阶Hessian信息对剩余权重进行矫正，补偿量化引入的误差，从而最小化量化前后模型的输出差异。即，GPTQ 对当前权重进行量化，然后更新剩余权重以最小化量化前后，层输出的损失。

GPTQ建立在传统算法OBQ的基础上。OBQ通过相对于未量化权重的Hessian矩阵的重建误差的方法，来实现每行权重矩阵的最优量化顺序。在每个量化步骤之后，OBQ迭代调整未量化的权重以减轻重建误差。然而，量化过程中频繁更新Hessian矩阵增加了计算复杂度。

GPTQ作者认为当今模型过于复杂，导致求解整个模型的海森矩阵太复杂。如果假设参数矩阵的同一行参数互相之间是相关的，而不同行之间的参数互不相关，则只需计算行内海森矩阵即可。GPTQ作者认为剪枝是一种特殊的量化，同时提出OBQ：逐层求海森矩阵并按影响从小到大给层内权重排个序，然后依次量化。

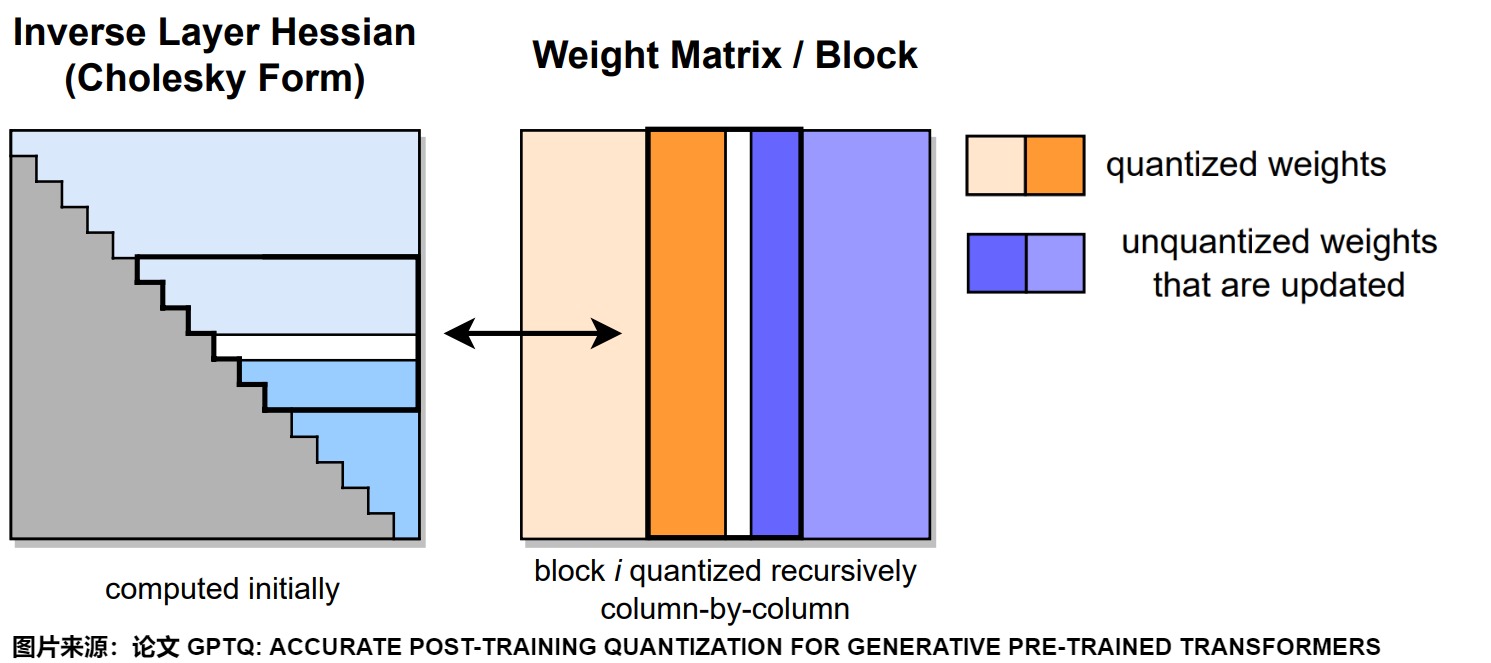
下图给出了GPTQ量化过程。在给定的步骤中，GPTQ 使用Cholesky分解中存储的逆Hessian信息对连续列的块（粗体）进行量化，并在步骤结束时更新剩余的权重（蓝色）。量化过程在每个块内递归应用。白色中间列代表当前正在被量化的部分。右图黑色方框就是一个block，表示当前正在进行量化的组。

2.1.1 背景

在GPTQ之前，主要PTQ方案最高只能实现8位量化，GPTQ进一步探索更低比特的量化。GPTQ 并不是凭空出现的，它的基础有两个：

逐层量化。
Optimal Brain Quantization (OBQ)。

逐层量化

GPTQ使用非对称量化，并且逐层进行，每层独立处理完毕后再继续到下一层。采样逐层量化相当于对每层求解一个重建问题。给定线性层 ℓ 的权重 Wℓ 和输入 Xℓ ，优化目标为找到一个量化的权重矩阵 $\widehat W$ ，使得其相对于全精度层的输出的平方差最小。下面公式中，W和$\widehat W$分别表示原始权重和剪枝后的权重矩阵，X 表示矩阵形式的输入。

\[arg⁡min_\widehat W||WX−\widehat WX||^2_2 \]

若将权重矩阵按行分解，则剪枝损失又可以表示为按行求和的形式。由于每次迭代我们都只对某一行中的一个权重进行剪枝，也就是说只影响一行的剪枝损失。进而，每一次迭代只影响当前行的 Hessian 矩阵，不同行之间的 Hessian 矩阵计算是相互独立的，所以不同行之间的迭代是可以并行的。

OBQ

GPTQ的原理来自于另一个量化方法OBQ(Optimal Brain Quantization)，OBQ 实际上是对 OBS(Optimal Brain Surgeon，一种比较经典的剪枝方法）的魔改，而OBS则来自于OBD（Optimal Brain Damage，由 Yann LeCun 在1990年提出的剪枝方法）。

OBD的作用是：引入二阶导数信息对神经网络进行最小损失剪枝。
OBS的作用是：引入删除权重补偿概念，使得剪枝损失降到最小。

因此，我们要梳理一下脉络。我们的核心问题是：如何选择性的删除一些权重来减少网络大小的同时，不要引入太多的误差？由此而来的是，如何定义删除权重带来的误差是什么？或者说如何衡量？

OBD

OBD是剪枝方案，模型剪枝实际上就是将 W 的某个值调整为 0。因此，我们可以通过删除某权重参数所带来的损失函数的变化来衡量该权重参数的重要性。即，如果要在模型中去除一些参数（即剪枝），我们希望去除对目标函数E影响小的参数。但是，删除一个参数再重新评估目标函数的方法是在是太繁杂了。因此OBD建立了一个误差函数的局部模型来预测扰动参数向量（删除部分权重参数）对优化目标造成的影响。

假设模型的权重为 W，损失函数为 f，则在当前权重下，模型的训练损失为 L=L(W)。OBD 的基本思想是以模型训练损失为目标函数，迭代地选择剪枝参数使目标函数最小化。OBD 作者对目标函数 E 做泰勒展开来估计权重调整造成的影响。同时，作者做了一些假设（如：假设删除任意一个参数后，其他参数对目标函数的影响不变。也就是说，每个参数对目标函数的影响是独立的），然后进行简化。最终得到一个方案：对目标函数的变化量被简化为$\frac{1}{2}h_{ii}w_i^2$，只要计算海森矩阵 $h_{ii}$ ，就可以知道每个参数对目标的影响。然后就可以按照影响从小到大给参数排个序，这样就确定了参数剪枝的次序。具体参加下图。

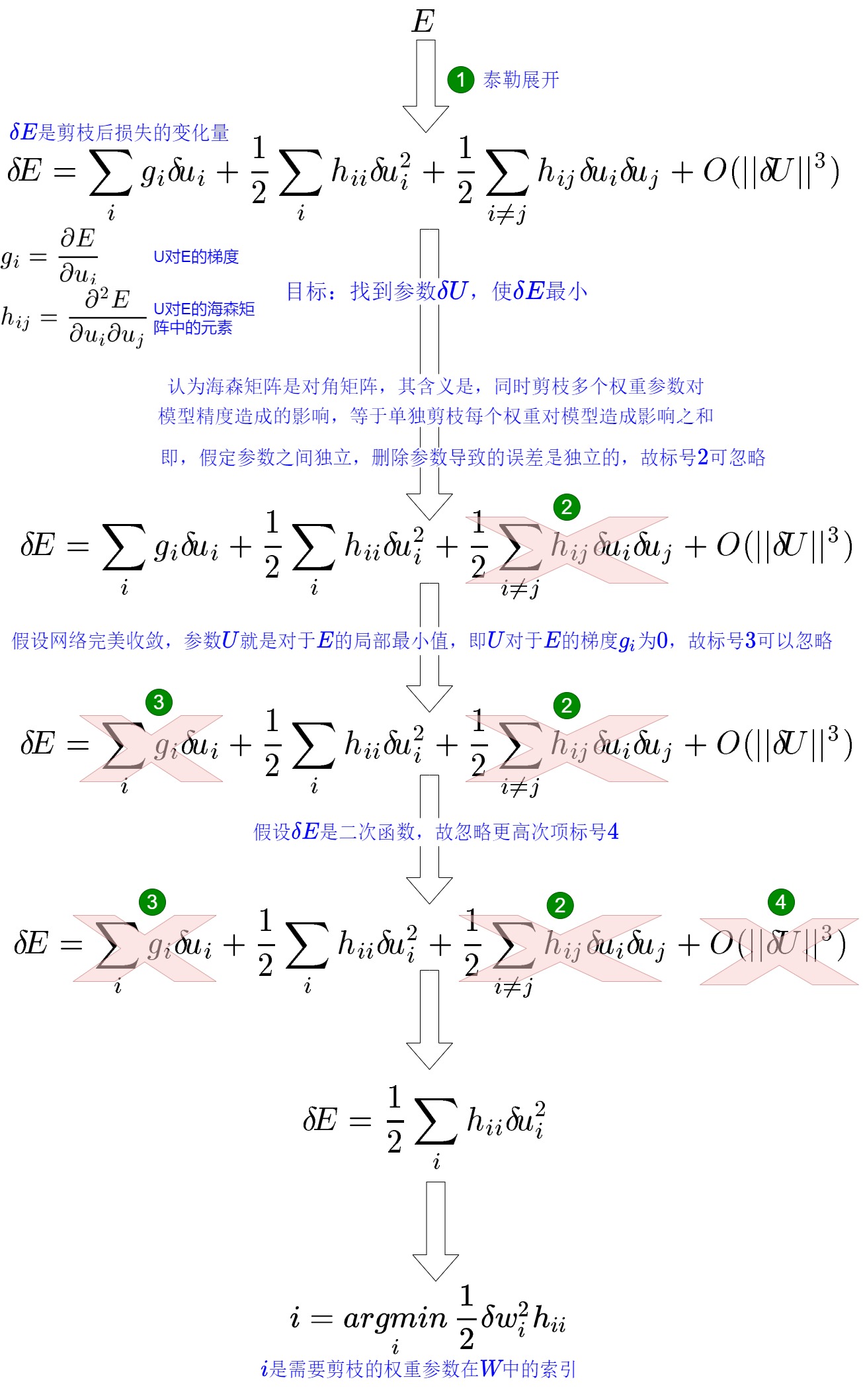
OBD剪枝算法如下：

构建神经网络；
训练神经网络直到收敛；
计算每个参数的二阶导数$ℎ_{𝑖𝑖}$；
按照Δ𝐸计算每个参数会带来的损失函数增加值；
删除一些Δ𝐸小的系数；
重复2-5直到删除的数量达到预设要求。

OBS

OBS 肯定了 OBD 关于减小模型剪枝对损失函数影响的思路，但是OBS认为OBD中提出的参数之间的独立性假设不成立，OBS 认为权重剪枝之间是有关联的，我们还是要考虑交叉项，所以不能简单地将 Hessian 矩阵假设为对角矩阵。

具体而言，OBS 认为，参数之间的独立性不成立，因此，还是要考虑交叉项。假设我们要抹去一个权重记为 $w_q$，使得其对整体的误差增加最少，但是，同时应该再计算出一个补偿$\delta_q$应用于剩余的权重上，使得抹去的这个权重所带来的误差被抵消。

OBS作者找到了一个方法：通过求解海森矩阵的逆，就可以计算每个参数权重$w_q$对目标的影响$\frac{1}{2}\frac{w_q^2}{[\mathbf{H^{-1}]_{qq}}}$，然后就可以按照影响从小到大给参数排个序，这样就确定了参数剪枝的次序。同时，每次剪枝一个参数，其他的参数也更新一次从而减少误差。

OBS 最终算法如下图所示：把权重直接展开，计算对应的海森矩阵，然后按照顺序进行量化。

其实，OBS研究的是量化视角下的参数敏感度。并非神经网络中的所有参数都同等重要。直观地说，如果某个权重的舍入误差（rounding error）较大，则可以将其视为具有较大的量化参数敏感度，即这个权重和量化点不接近。直接统计权重的舍入误差忽略了 LLM 向量相关性非常大的事实，需要进行合理补偿：权重 $w_a$ 可能有较大的舍入误差，但 $w_a$ 与另一个权重 $w_b$ 密切相关，这意味着可以通过向下舍入 $w_b$ 很好地补偿对$w_a$进行舍入的误差。

OBS 在每次迭代中，都涉及到计算 Hessian 矩阵的逆矩阵。设权重参数总量为 d，则计算 Hessian 矩阵的逆矩阵的时间复杂度为 $O(d^3)$，且每次迭代都需要计算一次，因此 OBS 的时间复杂度为 $O(d^4)$。显然对于动则上百万甚至上亿参数的模型来说，这种方式的计算量是非常巨大的。

OBQ

OBQ 把OBS 推广到模型量化中，同时加上分行运算的方式。模型剪枝是把某些权重变成 0，而模型量化则是把权重近似到一个值。因此，可以把剪枝理解成为一种特殊的量化。OBQ 使用贪心算法对权重W矩阵分行独立计算，每一行内部量化的时候按照Δ𝐸最小的原则来选择量化的顺序。具体而言，OBQ 逐层量化的公式可写成 W 每一行的平方差的和，从而以贪婪的方式进行量化：

利用海森矩阵信息作为准则判定每个权重量化后对输出loss造成的影响。选择让当前权重 W 量化误差（通过Δ𝐸找到在本行内量化导致损失函数增加的最小的系数）最小的一行权重 w 进行量化；
对其它未量化的权重进行更新以弥补量化损失。

具体推导如下图所示，其中 quant(w) 是把 w 近似到最近的quant grid的点上，简单说就是四舍五入到指定位数上。可以看到假如quant(q)永远返回零，其实就是原版的OBS。

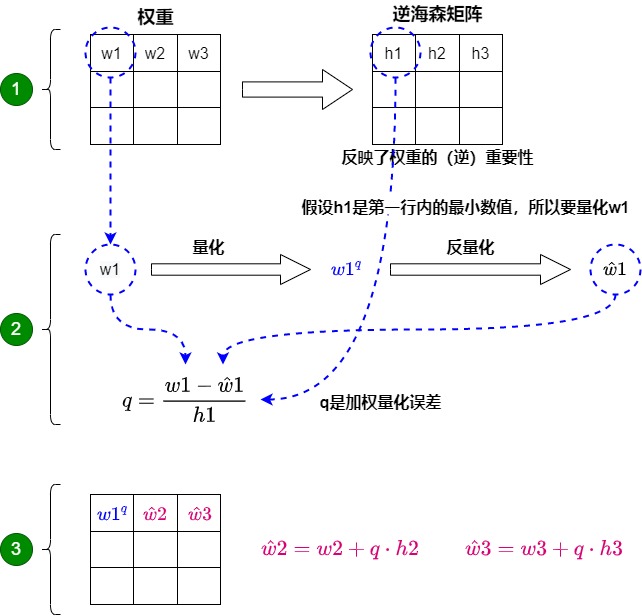
这个方法之所以行之有效，是因为权重通常是相互关联的。所以当一个权重发生量化误差时，相关的权重会相应地更新（通过逆海森矩阵）。具体过程如下图所示：

首先将层的权重转换为逆海森矩阵（Hessian）。海森矩阵是模型损失函数的二阶导数，它告诉我们模型输出对每个权重变化的敏感度，本质上展示了每个权重在层中的（逆）重要性。在逆-海森矩阵中，较低的值表示更"重要"的权重。因为这些权重的小变化可能会导致模型性能的显著变化。即，调整过程会优先考虑对精度至关重要的权重，有效地生成加权量化误差，从而保留更重要的细节。
对权重矩阵中的第一行的第一个权重进行量化，然后反量化。这个过程允许我们计算量化误差（q），我们可以使用之前计算的逆海森（h_1）来加权这个量化误差。本质上是根据权重的重要性创建了一个加权量化误差。
OBQ不会让量化误差孤立地存在于单个权重上，而是将这个加权量化误差重新分配到行中的其他权重上。这有助于维持网络的整体功能和输出。例如，如果我们对第一行的第一个权重（w1）进行量化，我们会将量化误差（q）乘以第一行的另外两个权重来进行弥补误差损失。即，对其他权重进行更新来调整权重，补偿权重w1量化导致的影响。我们重复这个过程，将加权量化误差重新分配，直到所有值都被量化。

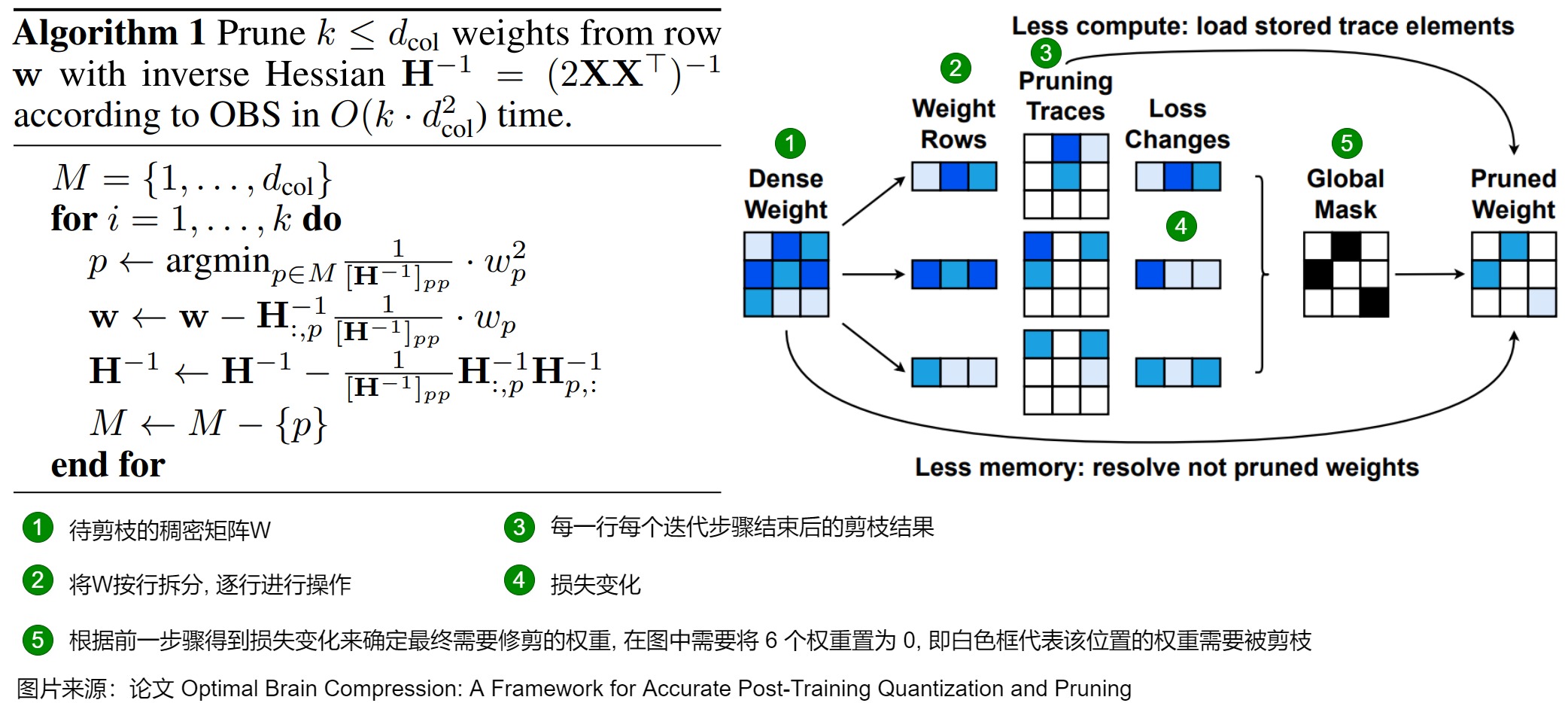
论文给出的算法如下。

左数第一列是待剪枝的稠密矩阵 W。
左数第二列表示将 W 按行拆分, 准备逐行进行操作。
左数第三和第四列表示逐行按照算法进行剪枝。
- Pruning Traces 表示每一行每个迭代步骤结束后的剪枝结果。
- Loss Changes 表示每个迭代步骤后损失的变化量，颜色越深表示损失越大。
左数第五列表示根据前一步骤得到 Loss Changes 确定最终需要修剪的权重, 在图中需要将 6 个权重置为 0, 即白色框代表该位置的权重需要被剪枝。
Less compute: load stored trace elements, 表示如果存储了 Pruning Traces 时，可以不用重新跑剪枝过程.
Less memory: resolve not pruned weights, 表示如果没有足够空间可以存储 Pruning Traces 时，再逐行重跑一遍剪枝过程或者直接进行一次参数更新就能得到这一行的剪枝结果。

总的来说，OBQ方法通过迭代和更新权重的方式，以贪心策略找到最佳的量化参数，以最小化量化引入的误差，同时控制模型的大小。这种方法允许在后训练阶段将神经网络的权重量化为所需的精度，而无需重新训练整个模型。这种策略对于大型语言模型如GPT非常有用，因为它们通常需要在保持高准确性的同时减小模型尺寸。

虽然 OBQ 不错，但是太慢，因为对于包含$d_{row} \times d_{col}$的权重矩阵 W，OBQ的计算复杂度是O $(d_{row}⋅d_{col}^3)$。OBQ 使用一小时左右量化一个 ResNet50，在大模型（如：GPT3）上可能要数天。

2.1.2 GPTQ 方案

特色

GPTQ 的特点或者说主要改进如下：

逐层量化。GPTQ进行逐层进行非对称量化，每层独立处理完毕后再继续到下一层。
按固定顺序量化。GPTQ作者觉得对于LLMs来说，每次都要挑选需要量化的参数是不必要的。因为，在量化的过程中，虽然以贪心算法来每次以最小的误差来量化权重的方法表现良好，但相比固定顺序并没有明显提升，尤其是在大模型上可能固定顺序更好。因此，GPTQ将每一行的量化权重选择方式从OBQ的贪心策略改成固定地按索引顺序选择。这种方法使得在大型模型上的计算效率更高，因为它减少了计算复杂性。
Lazy Batch-Updates。如果我们每次量化一个参数就进行一次权重更新的话，更多的时间都被花到访存，不能充分利用GPU的算力，所以 GPTQ 选择分批进行更新，批内完成后再更新全局的矩阵。这样可以延迟一部分参数的更新，缓解 I/O 压力。
Cholesky(乔莱斯基) 分解。GPTQ发现逐权重量化需要频繁更新整个海森矩阵的逆，这会引入数值误差。因此用 Cholesky 分解求海森矩阵的逆，在增强数值稳定性的同时，不再需要对海森矩阵做更新计算，进一步减少了计算量。结合 Lazy Batch-Updates, 可以将权重更新式限制在 block 内, 然后再通过一次更新将此 block 之后的全部列进行更新. 这样就起到了节省内存带宽的作用, 从而显著提升算法效率。
GPTQ首次将4bit/3bit权重量化应用在176B的模型上，同时也提供了对应的kernel。

取消贪心算法

OBQ采用贪心策略，独立量化权重矩阵W的每一行，每一行内部量化的顺序不同，都在维护自己的最优量化顺序：按照ΔE最小的原则来选择量化的顺序。即，每个权重是按"贪心顺序"选择的，总是优先量化当前对整体误差影响最小的那个权重。这个策略虽然理论上更优，但在大模型中效率极低。原因是：每次量化一个权重都需要更新 Hessian 的逆矩阵，且每行都需要独立执行，导致总时间复杂度极高。

GPTQ发现对于参数量很大的层，这样严格选择顺序的量化结果和任意顺序的量化结果差别并不大，即使不使用贪心策略，只要采用任意固定顺序来量化每一行中的权重，最终的误差几乎和贪心顺序一致。GPTQ 作者分析：少数权重带来较大的量化损失，这些损失可以被剩余未量化的权重平衡掉，因此量化顺序可能不重要。因此，GPTQ提出所以决定对所有的行都使用同样的顺序进行量化，虽然理论上不是局部最优，但整体误差变化非常小，尤其在参数数量大的时候几乎无影响。

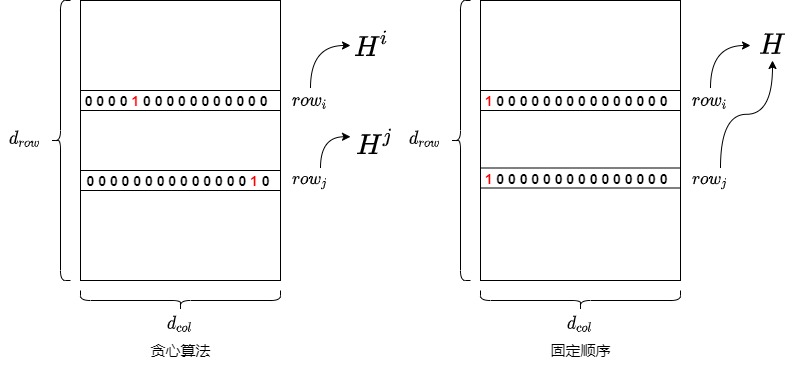
这样做的好处如下：

对于权重矩阵的每一行来说，其初始 Hessian 矩阵$H=2XX^T$只与输入矩阵 X相关，因此初始 Hessian 矩阵都是相同的。
在 OBQ 中，随着剪枝过程的进行，每一行权重的优化顺序都可能不一样，因此每一行相关的 Hessian 矩阵都会发生不同的变化。具体而言，每量化一个参数，都需要更新$H^{−1}$。如果每一行的量化顺序不一致，那么每一步中，各行的$H^{−1}$是不一样的，需要各自单独计算。
而如果每一行的量化顺序一致，那么每一步各行的$H^{−1}$是一样的，所有行共享一个逆 Hessian 矩阵只，且需要计算一次即可，这种方式也节省了每次构造 H(i) 的时间。再考虑到所有行都是按照一样的顺序来量化权重，那么一次迭代就可以量化同一列的所有行。这项改进使得数矩阵每一行的量化可以做并行的矩阵计算。
由于大模型极度冗余，单个权重引入的误差影响微小，统一顺序导致的子最优选择不会积累为显著性能损失。GPTQ 中使用的 Hessian-based 误差补偿机制会在每一步自动对未量化权重进行调整，进一步抑制误差传播。

这项改进使得参数矩阵每一行的量化可以做并行的矩阵计算（即 per-channel quantization）。对于大模型场景，使得量化速度快了一个数量级。

Lazy Batch-Updates

因为大模型权重的海森矩阵很大，OBQ 每次迭代都需要更新整个海塞矩阵的逆以及对整个权重进行更新，这一过程涉及大量的内存访问，但实际的计算量却较少。所以算法的计算访存比相对较低，性能瓶颈实际在于GPU的内存带宽。具体而言，因为每量化1列参数，就需要更新1次海森矩阵的逆，假设逆矩阵的大小为 $d_{row} \times d_{col}$ ，共需更新 $d_{col}$次，带来的访存总量为 $d_{row} \times d_{col}^2$ 。当维度较大时，则会导致运行时间都被访存占用。例如，在量化某个参数矩阵的情况下，每次量化一个参数，其他所有未量化的参数都要按公式全都要更新一遍。

作者发现：同一个特征矩阵W不同列间的权重更新是不会互相影响的，具体如下：

当前列 i 的量化只受到前序列量化的影响（前序列量化后会更新后续列参数）。
当前列 i 的量化不会影响前序已经量化的列（前序列量化完成后其参数固定）。
当前列 i 的量化会更新后续列的参数，但后续列的更新不会影响当前列 i 的量化。换句话说，当前列的量化不会受到尚未更新的列的影响。

具体如下图所示，由于参数量化是一列一列按次序进行的，第 i 列的参数的量化结果受到前 i-1 列量化的影响，但第 i 列的量化结果不影响前面列的量化。因此我们不需要每次量化前面的列，就更新一遍第 i 列的参数，而是可以先逐步记录量化前面列给第 i 列带来的更新量，在量化到第 i 列时，再一次性更新参数，这样就可以减少 IO 的次数。

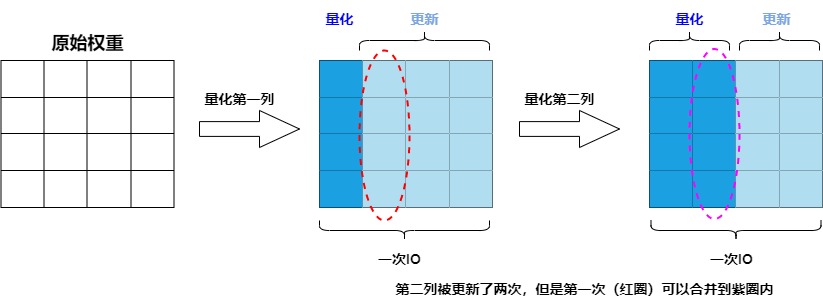
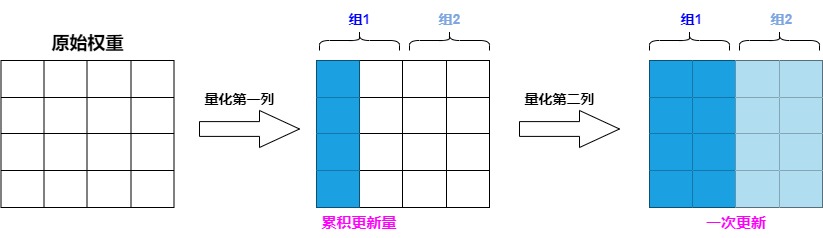
因此作者提出了延迟批处理的方法：先延迟一部分参数的更新，再后续一次处理多个列，以此来缓解带宽的压力，大幅提升了计算速度。具体如下：

对权重矩阵按每 B= 128 列进行分组（分成group/block），量化当前列后，调整该组剩余的权重，以补偿量化引入的误差，这样可以将更新限制在这些列和的对应BxB块中。

当一个 group 的参数全部量化完成，我们才使用下面这个多权重版本的公式统一对 $H^{−1}$ 和 W 进行一次全局更新，即处理完当前组的所有列后，再更新整个矩阵的其他列组（其他128列组），以进一步修正误差。这一完整过程就是"惰性批量更新"（Lazy Batch Update）。

这种方法没有减少理论的计算总量，但避免了大量更新Hessian矩阵的需要，有效缓解了访存的瓶颈，从而加快了整个量化过程。

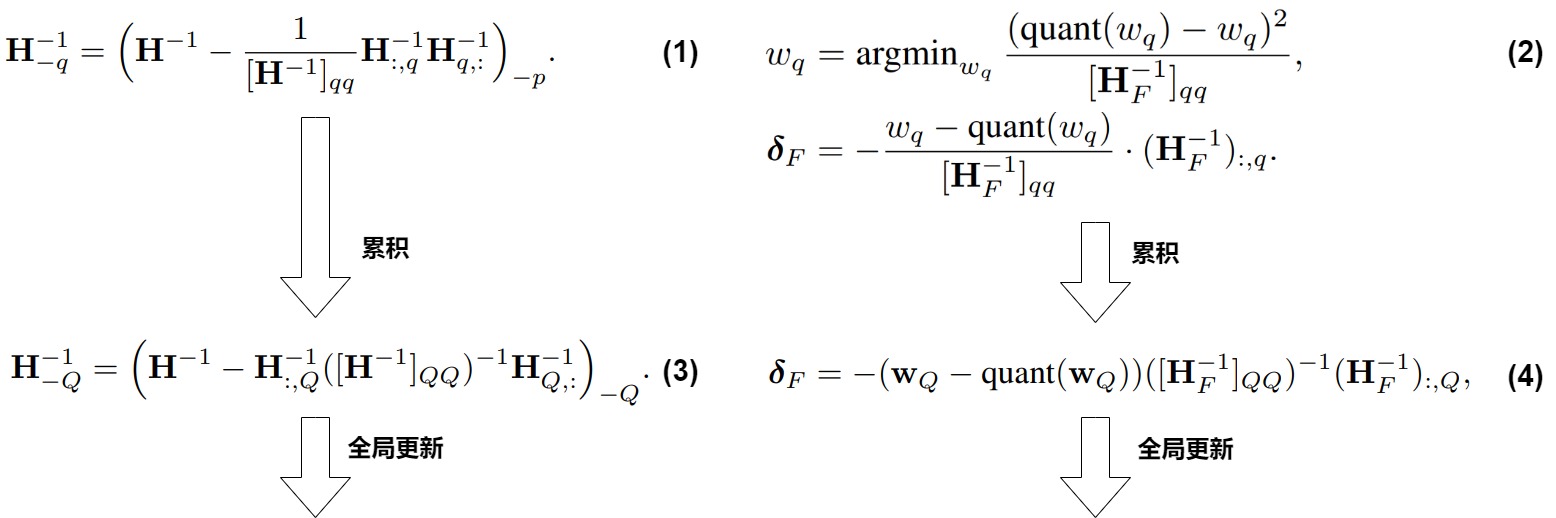
Cholesky(乔莱斯基) 分解

GPTQ 还应用 Cholesky 分解来解决 H𝐻 逆矩阵计算的数值稳定性问题。 GPTQ 作者在实验过程中注意到在大规模参数矩阵上重复的应用如下公式会累积误差，进而使得数值计算不准确。确切的说，矩阵$H^{-1}_F$会出现无穷的情况，这回导致算法更新剩余权重错误，导致量化效果变差。

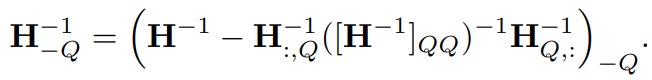
想解决此问题，对于小模型，在 H 的对角线元素添加小的常数项 $\lambda$ 即可，对于大模型需要更稳定和通用的办法。为了解决这个问题，作者用Cholesky 分解（一种分解矩阵的方法）来求海森矩阵的逆，提前计算好所有需要的信息，并使用优化的Cholesky核进行加速。

总体算法

GPTQ根据输入的Hessian逆矩阵$𝐻^{−1}$ 和其他参数来量化权重W，并且核心思想是通过迭代逐步量化权重以减小误差。GPTQ算法的主要步骤如下。

初始化量化结果Q为一个零矩阵，初始化误差矩阵E为一个零矩阵。
对$𝐻^{−1}$ 进行Cholesky分解，得到H−1的逆矩阵信息。
迭代处理权重列的量化（逐列量化权重矩阵，并在每一步调整尚未量化的部分以补偿上述量化误差）：
- 对每个列进行量化，更新Q矩阵中的对应列。
- 计算量化误差，更新误差矩阵E。
- 更新权重矩阵W中的权重，以减小误差。
- 重复上述步骤，直到所有的权重列都被量化。
最终，返回量化后的权重矩阵Q。

为了降低计算复杂度，GPTQ 采用了逐列优化的方法。将权重矩阵 W 的列表示为 wi，对每一列进行量化，同时考虑之前列量化引入的误差累积。逐列优化的主要优势在于：

降低计算复杂度：将高维的矩阵优化问题分解为多个低维的向量优化问题。
考虑误差累积：在每一步更新中，考虑了之前量化引入的误差，保证了整体误差的最小化。

这里做几点简要说明:

这里的算法流程对权重的每一行是并行处理的
算法第 3 行左侧的 $𝐻^{−1}$ 实际上是 $𝐻^{−1}=𝐿𝐿^𝑇$ 中的 $𝐿^𝑇$
算法的倒数第 5 行的分子进行平方后除以 2 才代表了本次迭代造成的损失增量
算法的倒数第 4 行实际上还更新了被量化的权重项本身, 更新后其权重为 0, 而被量化的权重所在列靠前的权重的更新项实际上是 0, 因此可以统一这么写
算法倒数第 2 行表示对 block 之后的全部权重进行一次性更新, 实际上也就是倒数第 4 行将列的范围 𝑗:(𝑖+𝐵) 扩展到 𝑖+𝐵。

虽然前面的 GPTQ 通过校准数据最小化量化误差，提升量化效果。但是可能过拟合校准集，导致模型在分布外域上的性能下降。

2.2 AWQ

论文"AWQ: Activation-aware Weight Quantization for LLM Compression and Acceleration"是SmoothQuant的续作。论文作者发现：对模型的性能来说，权重并不是同等重要的。极少量（0.1%~1%）的参数可能主导的量化过程中损失的性能。保留这些显著权重（Salient weight）不做量化，就可以显著减少量化误差。什么样的权重值得保护呢，作者指出，应该参考 activation 分布而不是 weight 分布。在推理时被显著激活的权重肯定更重要，因为这些权重处理更重要的特征。即用激活值来发现重要的weight，较大激活值对应的权重比较重要。在此观察的基础上，AWQ采用了激活感知方法。该方法是一种数据驱动的方法，采用逐通道缩放技术来自动搜索最佳缩放因子，通过保护更多的 "重要" 权重来提高准确性，从而在量化所有权重的同时最小化量化误差。

2.2.1 动机

AWQ作者有以下发现：

LLM 的权重并非同等重要。与其他权重相比，有一小部分显著权重对 LLM 的性能更为重要。作者认为，保留这些显著权重不进行量化（维持这些权重的精度为FP16），其他权重使用低比特量化推理，就可以在不进行任何训练的情况下，弥补量化损失造成的性能下降。
激活大的值所对应的权重为重要权重。可以根据激活幅度（magnitude）选择权重，通过只保留 0.1%-1% 的较大激活对应权重通道，对显著权重进行放大，就可以防止高影响力权重的退化，保留了大型语言模型中的关键知识，显著提高量化性能。

2.2.2 方案

选择权重

通常评估权重重要性的方法是查看其大小（magnitude）或 L2-norm（L2-范数）。

但是AWQ作者发现，保留那些具有较大 Norm的权重通道对量化性能的提升有限。与随机选择效果相比，仅仅有少量改进。而根据激活幅度（magnitude）选择权重可以显著提高模型量化效果。作者推测是，幅度较大的输入特征通常更重要，保留相应的权重为 FP16 可以更好地保护这些特征，从而提升模型性能。具体实现上，作者是对激活值的每一列求绝对值的平均值，然后把平均值较大的一列对应的通道视作显著通道，保留 FP16 精度。

然而在实现中遇到一个问题：尽管将 0.1% 的权重保留为 FP16 可以在不明显增加模型大小的情况下提高量化性能，但这种混合精度数据类型会给系统实现带来困难（硬件效率低下）**。**因此，我们需要想出一种方法，即保护重要的权重，同时又不用实际保留它们为 FP16。具体如下图所示，RTN代表vanilla round-to-nearest baseline。

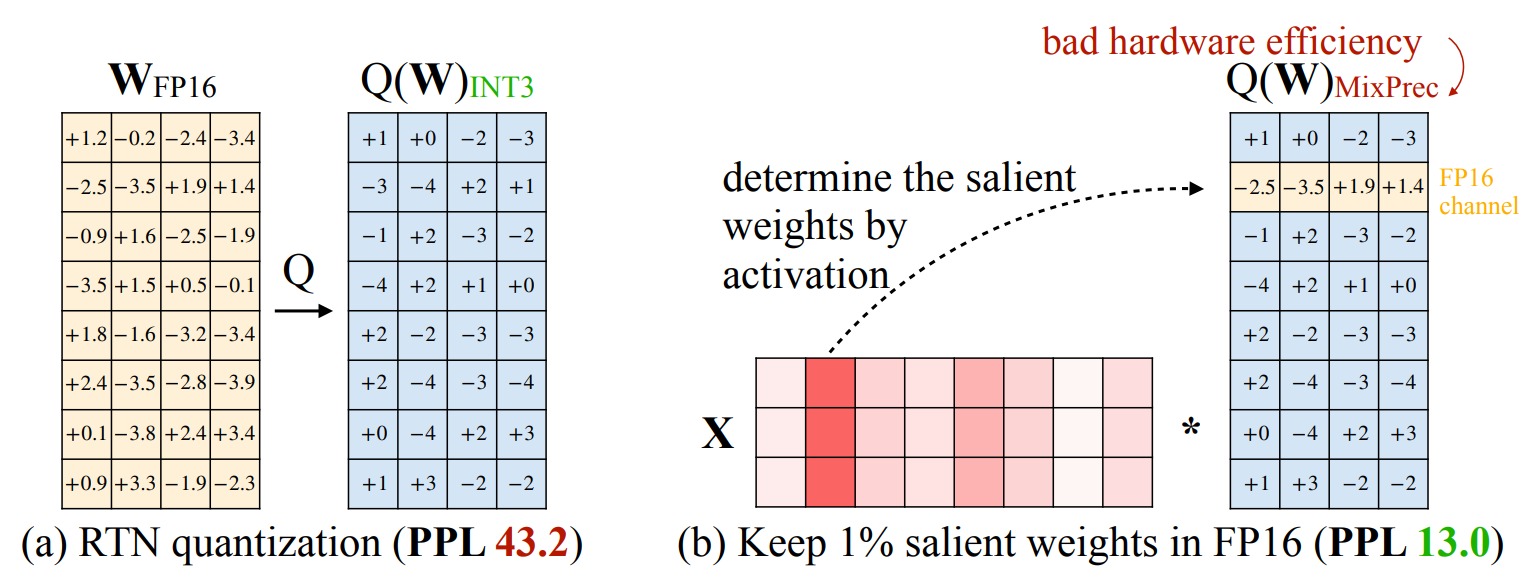
激活感知缩放

AWQ的思路是：通过激活感知缩放（Activation-aware Scaling）保护显著权重。即，识别每一层中最重要的权重，通过按逐通道（per-channel）缩放 (Scaling) 来减少重要权重（Salinet Weight ）的量化误差。这些权重对于维持模型性能至关重要。通过关注与高激活特征对应的权重，AWQ最小化了可能导致显著精度下降的量化误差。具体如下图所示。

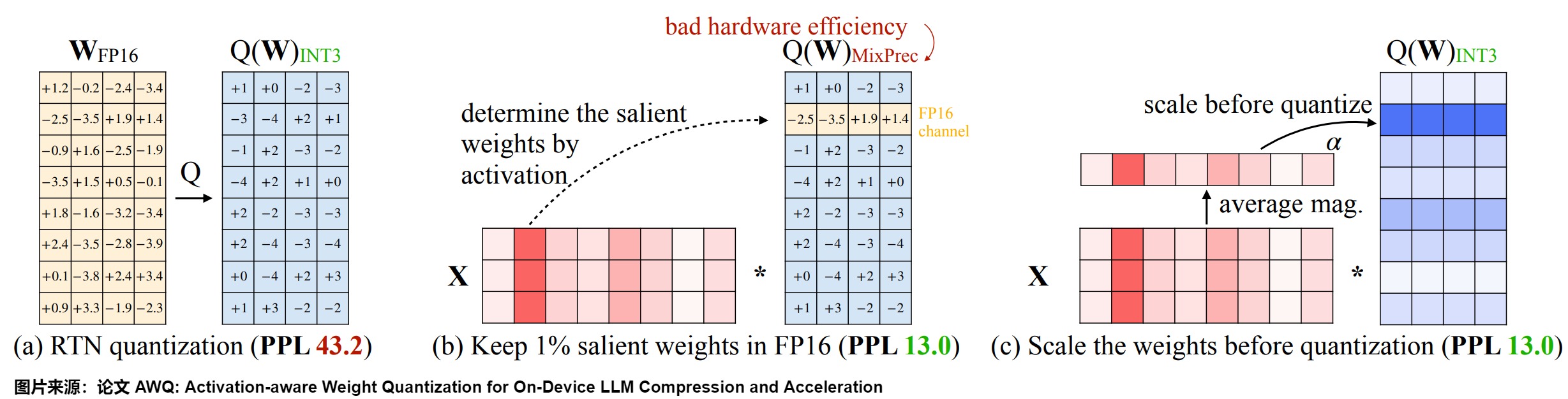
推导

保护异常值权重通道的一种直接方法是将通道乘以一定的缩放比(scaling ratio >1)，这样它们就可以精确量化。我们接下来分析采用缩放比前后，Weight-only的量化误差。由下图可知，方案基本可行。

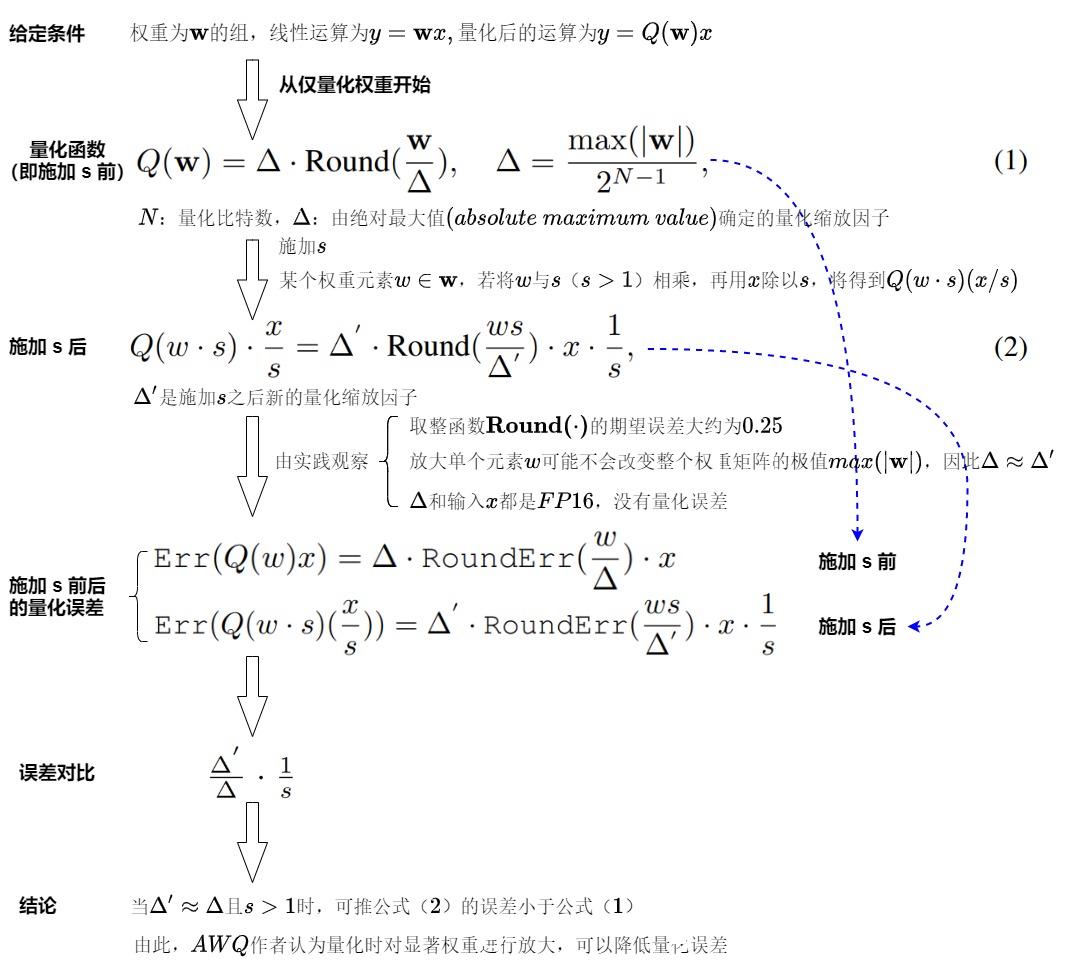
问题

如果希望重要的权重被更好地表示出来，就需要设置更大的缩放比，这样量化效果更好。但如果我们使用非常大的缩放比，非显著权重的channel（(Non-salient channels）会被迫使用更小的动态范围，这可能会损害模型的整体精度。即，s进一步增大时，$\Delta' \approx \Delta$不再成立，当 Δ 增加时，非显著通道的相对误差将会增加（非显著通道的误差将被放大），从而使得量化精度下降，没有保留 1%权重方法效果好。因此，在保护 Salient Channels 时，还需要考虑如何减少 Non-salient channels 的错误。

最优缩放因子搜索

为了同时考虑 Salient Weight 和 Non-salient Weight，AWQ 提出了自动搜索 (每个输入通道) 最优缩放比的方法（找到一个合适的缩放因子s），使得减少显著权重量化损失的同时也不能增加其它权重的量化损失，让某一层量化后的输出差最小。

下图给出了思路。形式上，希望优化下图中标号1的目标函数。但是因量化函数是不可微的，故无法用反向传播直接优化问题。有些优化技术因为依赖于近似梯度，所以仍然存在收敛不稳定的问题。为了使整个过程更加稳定，AWQ 作者通过分析影响比例因子选择的因素，来定义最优 Scaling 的搜索空间。

如前文所述，权重通道的显著性实际上是由 activation 的尺度（scale）决定的（故此称之为 activation-awareness）。因此，作者简单地使用非常简单的搜索空间（如下图标号2）。此方法会自动搜索一个最优（每个输入通道）比例因子，并进一步应用权重裁剪来最小化量化的 MSE 误差，即，让某一层量化后的输出差异最小化。

如何确定超参数 $\alpha$？作者认为可以通过在区间 [0,1] 上进行快速网格搜索 来找到最佳的 $\alpha$（0 表示不进行缩放；1 表示在搜索空间中最激进的缩放）。通过阅读源码发现该方法实际上就是在 [0,1] 区间平均取 20 个数，0, 0.05, 0.10, 0.15 ...... 然后逐个计算不同 $\alpha$下的 MSE 损失，损失最小的就是最佳的 $\alpha$。

应用

awq 中需要根据模块类型，分别处理不同的线性层组，分开计算不同模块的权重缩放因子，比如可以将llm 模型分成以下几个模块分别计算 scales。

self-attention 的查询、键、值投影层
self-attention 的输出投影层
mlp 的第一个全连接层
mlp 的第二个全连接层
mlp 的 gate_proj 和 up_proj 线性层
mlp 的 down_proj 线性层

与 SmoothQuant 的关系

因为两篇论文作者都来自著名的 MIT HAN LAB 团队，所以我们进行分析。

相同点

都是后训练量化 (Post-Training Quantization PTQ)。
都有对一些 weight (及其对应的 input activation) 做 scaling，即 weight 乘以一个 scaling factor，对应的 input activation 除以这个 scaling factor。
都需要校准集确定 scaling factor 的值 (无需额外的训练)。

区别

量化精度不同：SmoothQuant 量化精度为 W8A8；AWQ 量化精度为 W4A16。
Scaling factor 的确定方法不同：SmoothQuant 的 scaling factor 是算出来的： $𝑠_𝑗=max(|𝑋_𝑗|)^𝛼/max(|𝑊_𝑗|)^{1−𝛼}$ ；AWQ 的 scaling factor 是搜出来的 $𝑠=𝑠_{𝑋^𝛼},𝛼^∗=arg⁡\\ min_𝛼⁡𝐿(𝑠_{𝑋\^𝛼})$ ，其中 𝑠𝑋 是 activation 的平均幅值。
Scaling factor 施加的 weight 不同：SmoothQuant 平等地对每个 weight (及其对应的 input activation) 做 scaling；AWQ 只对少量 (约 0.1%) 的 salient weight (及其对应的 input activation) 做 scaling。
AWQ 作者还开发了 TinyChat，一个高效灵活的 4 位设备端 LLM/VLM 推理框架。

2.3 LLM-QAT

论文"LLM-QAT: Data-Free Quantization Aware Training for Large Language Models"是大模型量化感知训练的开山之作。目前一些针对大模型的PTQ方法已被证明在低至 8 bit 的情况下也能表现良好。但是论文作者发现这些方法在较低比特精度下会出现问题。因此，论文研究了 LLM 的QAT，以进一步提高量化水平。作者还提出了一种 data-free 蒸馏方法，该方法利用预训练模型产生的生成，可以更好地保留原始输出分布，并允许独立于其训练数据来量化任何生成模型，类似于训练后量化方法。文中除了量化权重和激活之外，还量化了 KV 缓存，这对于提高吞吐量和支持当前模型规模的长序列依赖至关重要。

2.3.1 动机

与后训练相比，QAT通常会带来更好的准确性，因为模型从一开始就被训练来考虑精度降低的问题。此外，它允许模型继续训练或进行fine tune，这对大型语言模型至关重要。但是，使用QAT量化LLM在几个主要方面面临挑战：

大模型的训练从技术上来说很困难，对于算力资源要求比较集中。而且，QAT需要引入模拟量化的操作, 会引起显存&计算量进一步上涨，以及梯度mismatch的问题，从而增加训练成本以及影响Scaling Laws。
QAT需要训练数据，但是对于大模型来说，很难获取到这些训练数据。而预训练数据的庞大规模和多样性本身就是一个障碍，数据的预处理也很困难。
LLM 在 zero-shot 生成方面表现出色，并在量化后保持这种能力至关重要。因此，选择合适的微调数据集很重要。如果 QAT 数据域太窄或者与原始预训练数据分布存在显著不同，则可能会损害模型的性能。
由于 LLM 表现出独特的权重和激活分布，其特点是存在大量的异常值。因此，针对小型模型的最好的量化裁剪（clipping）方法，但该方法对于LLM来说并不是开箱即用的。
此外，尚不清楚量化感知训练是否遵循模型的缩放规律。

2.3.2 方案

Data-free 蒸馏

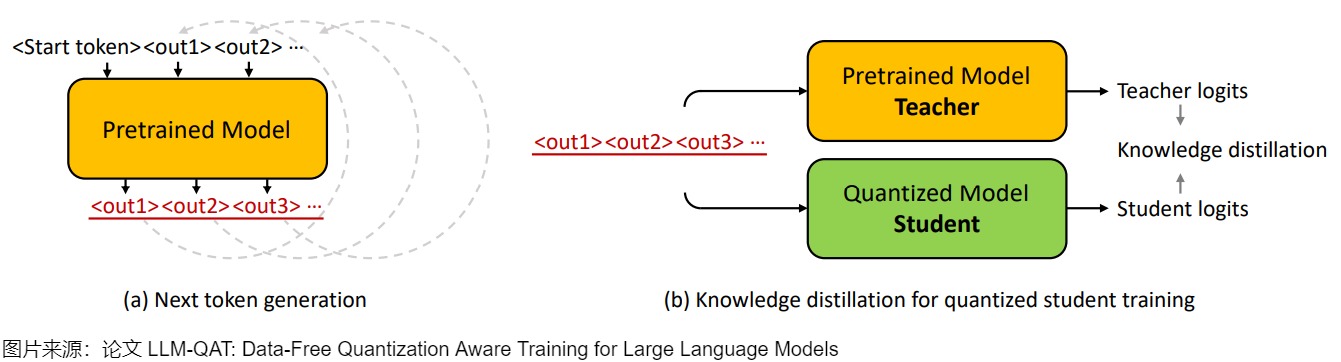
为了应对训练数据方面的挑战，需要将预训练数据的分布与有限数量的微调数据紧密的结合，论文提出了从原始预训练模型生成下一个 Token 数据的方法，并结合知识蒸馏来规避这个问题，该方法被称为 data-free 知识蒸馏，适用于任何生成模型，无论原始训练数据是否可用。

如下图(a)所示，我们从词汇表中随机化第一个Token：<start>，并让预训练模型生成下一个Token：<out1>，然后将生成的Token附加到起始Token以生成新的输出：<out2>。重复这个迭代过程，直到达到句子Token的结尾或最大生成长度。在数据生成过程中，从分布中采样下一个Token是非常重要的，作者在下一个Token生成时测试三种不同的采样策略。

最直接的方法是选择第 1 个候选者作为下一个Token。但是，下一个Token不一定代表训练学生模型的最佳标签，因为采样会引入固有的噪声。所以，该策略生成的句子缺乏多样性，并且会循环重复几个Token。
为了解决这个问题，论文使用预训练模型的 SoftMax 输出作为概率，从分布中随机采样下一个Token。这种采样策略会产生更加多样化的句子，并大大提高了微调学生模型的准确性。
此外，论文还发现最初的几个Token在确定预测趋势方面起着至关重要的作用。因此，对他们来说拥有更高的置信度很重要。在生成过程中，论文采用了混合采样策略，针对前 3~5 个Token确定性地选择 top-1 预测，然后剩余的Token进行随机采样。

实验表明，即使与使用原始训练集的大型子集进行训练相比，该方法也能够更好地保留原始模型的输出分布。此外，我们可以仅使用一小部分（100k）采样数据成功地提取量化模型，从而保证一个合适的计算成本。

知识蒸馏

论文作者使用基于交叉熵的 logits 蒸馏从全精度预训练教师网络来训练量化的学生网络，公式如下所示：

其中， i 表示当前批次中的第 i 个样本，总共有 n 个句子。 c 表示类的数量，在论文的例子中，它等于词汇量的大小。 T和S分别是教师网络和学生网络。

量化函数

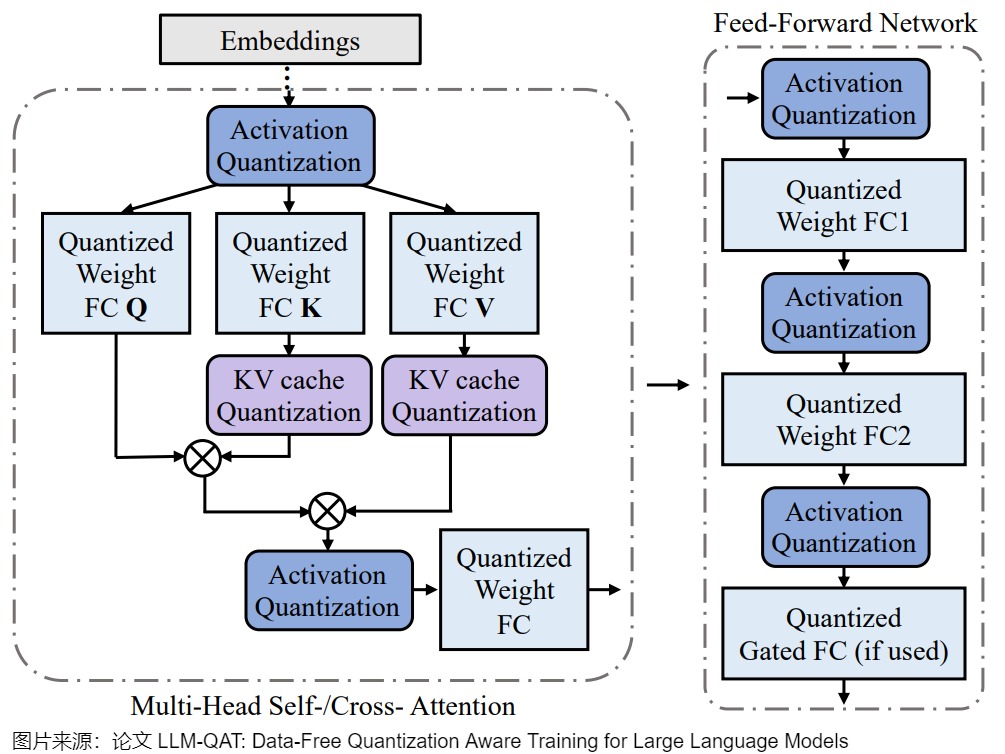
上图为量化 Transformer 模型的示例图。根据 Llm.int8 () 和 Smoothquant 中的发现，在LLM中，权重和激活都存在显著的异常值。这些异常值对量化过程有显著影响，因为它们会增加量化步长，同时降低中间值的精度。

但事实证明，在量化过程中裁剪这些异常值不利于 LLM 的性能。在训练的初始阶段，任何基于裁剪的方法都会导致异常高的困惑度（perplexity）分数（即> 10000），从而导致大量信息丢失，并且事实证明很难通过微调来恢复。因此，论文选择保留这些异常值。此外，论文还发现在具有门控线性单元（GLU）的模型中，激活权重大多是对称分布的。根据论文的分析和经验观察，论文为权重和激活选择对称 MinMax 量化，公式如下所示：

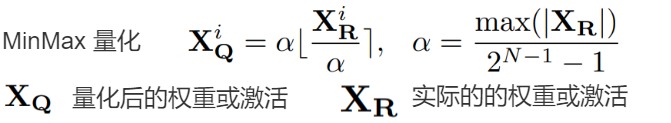
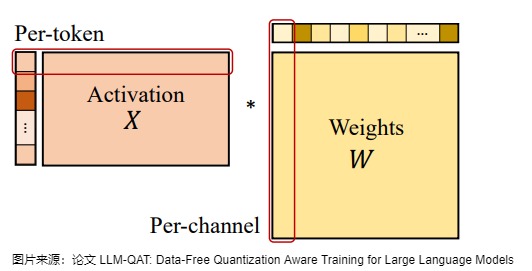
其中， XQ 表示量化后的权重或激活，XR 表示实际的权重或激活。为了确保有效的量化，论文采用 per-token 激活量化和 per-channel 权重量化，如下图所示。

KV Cache的量化感知训练

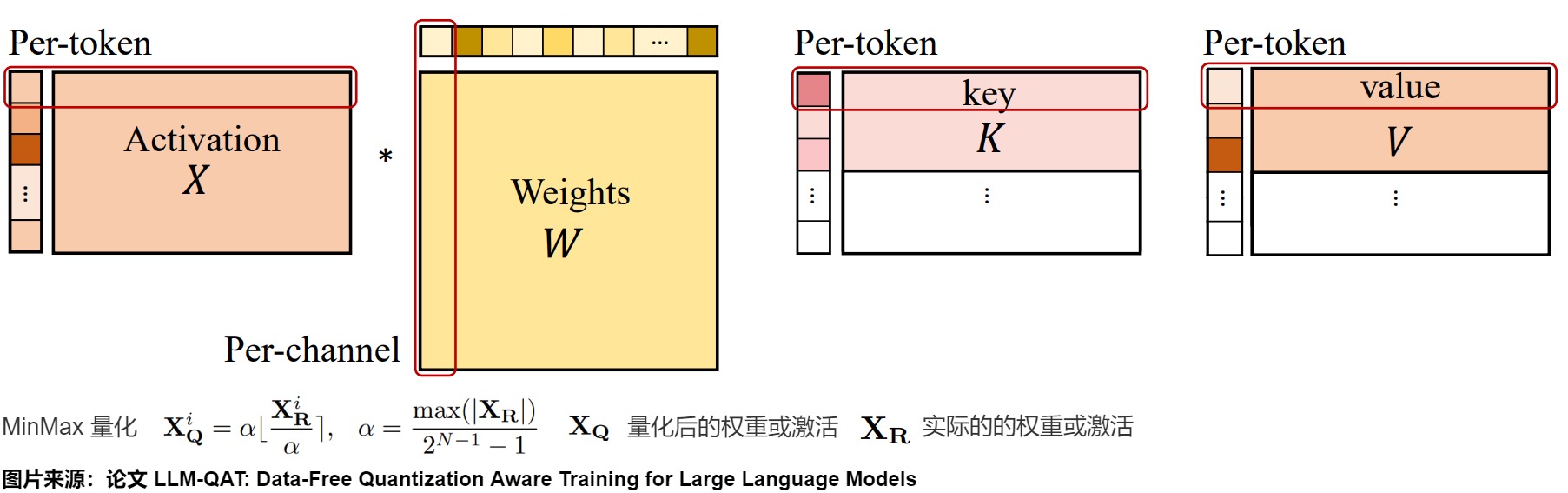
除了权重和激活之外，大语言模型（LLM）中的键值缓存（KV 缓存）也会消耗不少的内存。然而，之前只有少数工作解决了 LLM 中的 KV 缓存的量化问题，且方法主要局限于训练后量化（论文"FlexGen: High-Throughput Generative Inference of Large Language Models with a Single GPU"）。而本论文证明了可以采用用于激活量化的类似量化感知训练方法来量化 KV 缓存。

在训练过程中，LLM-QAT对 key 和 value 的整个激活张量进行量化，如下图所示。通过将量化函数集成到梯度计算中，确保使用量化的键值对进行有效的训练。

结论

论文采用了三种训练后量化方法 round-to-nearest(RTN)、 GPT-Q 和 SmoothQuant 作为基线，在BoolQ、PIQA、SIQA、HellaSwag、WinoGrande、ARC和 OBQA 数据集上针对不同的量化方法对比了常识推理任务的零样本性能，还在 TriviaQA 和 MMLU数据集上评估了不同的量化方法的小样本性能，同时，也在 WikiText2和 C4 数据集上对比了不同的量化方法的困惑度分数。其中，困惑度评估用于验证量化模型是否能够在其训练域的不同样本上保留模型的输出分布。零样本和少样本评估则衡量模型在下游任务上的能力是否得到保留。

对于从业者来说，一个重要的问题是是选择使用全精度的小模型，还是选择具有类似推理成本的较大的量化模型？虽然确切的权衡可能会因多种因素而异，但作者根据本文的结果提出了一些建议。

使用8比特量化的大模型应该优于较小的全精度模型，PTQ 方法足以满足这种情况。
使用 LLM-QAT 量化的 4 比特的模型应该优于类似大小的 8 比特模型。

因此，作者建议使用 4 比特的 LLM-QAT 模型，以实现最佳效率与精度的权衡。

2.4 QLoRA

QLoRA（Quantized Low-Rank Adapter）出自论文"QLORA: Efficient Finetuning of Quantized LLMs"，是首个基于LoRA（Low-rank Adapter）的PTQ方法，其中适配器位于每个网络层。通过一系列创新工作，如引入4位NormalFloat、双量化和Paged Optimizers（分页优化器）等方法，QLoRA对LoRA方法进行了更好的调优，在降低内存使用的同时，也可以保持性能。

在微调阶段，QLoRA首先将LLM量化为4位，然后，锁定原模型参数不参与训练，在更高的精度（如BFloat16或Float16）下，对量化模型的每个4位权重矩阵使用LoRA来进行微调。在推理阶段，QLoRA将LLM反量化到与LoRA相同的精度，然后将LoRA的更新添加到LLM中。

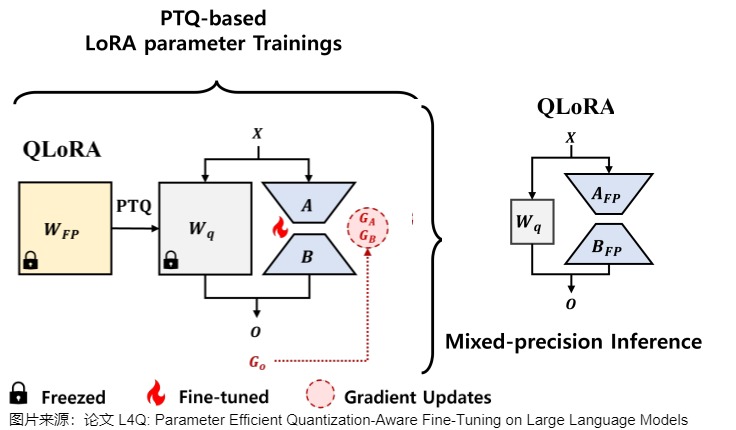
2.4.1 动机

由于模型量化前后存在量化误差，一个自然的想法就是用LoRA去学习这个量化误差。QLoRA就是在PTQ的过程中用一个全精度的LoRA矩阵去学这个量化误差。量化时权重采用NF4格式编码。

然而，由于LoRA参数上的额外前向路径，QLoRA在推理过程中还是需要和一个全精度的LoRA一起推理，计算全精度模型的加和，没法将LoRA融入到量化的模型里。这引入了计算效率低下的问题。这种低效是因为高精度LoRA参数和低精度量化权重不能合并为低精度值。本来想用量化的方式加速推理，现在只降低了显存开销。

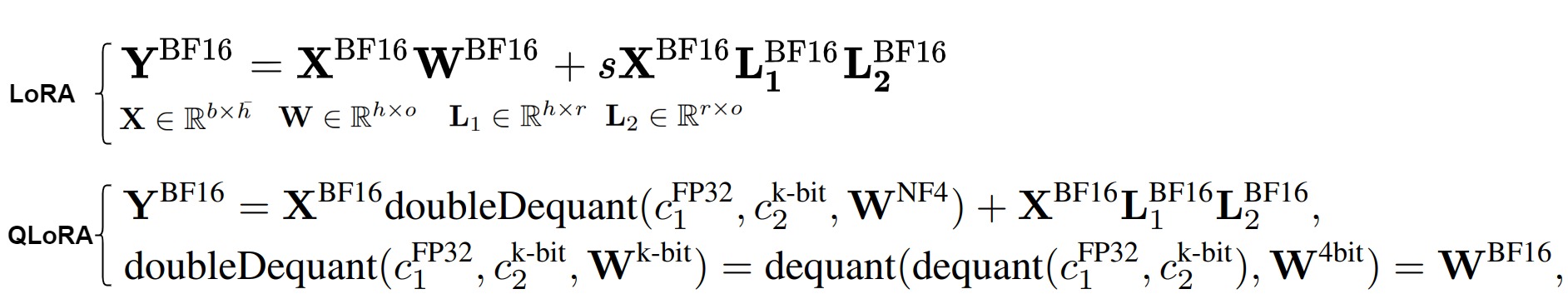
2.4.2 方案

QLoRA的主要创新如下：

4-bit NormalFloat (NF4) Quantization：QLoRA引入了一种新的4位量化数据类型，称为NormalFloat（NF4），它在信息理论上对于正态分布的权重是最优的，因此可以将权重量化为4位来减少内存占用的同时，也保持模型性能。
Double Quantization：QLoRA采用双重量化技术，即对普通参数进行一次量化，对量化常数再进行一次量化，这样可以进一步减少平均内存占用。
Paged Optimizers：为了管理内存峰值，QLoRA引入了分页优化器，它们使用NVIDIA统一内存来处理长序列长度的小批量数据时出现的内存需求。
Forward and Backward Propagation：在前向计算时，QLoRA首先通过反量化函数将原始模型的参数反量化成fp16，然后加上LoRA适配层。LoRA的参数不量化，因为它们需要反向传播优化。而原始模型的参数是冻结的，因此可以量化。在参数更新时，只需要计算LoRA适配器权重对误差的梯度，而不需要4位权重的梯度。

4位正态浮点量化

$\text{4-bit NormalFloat}$（正态浮点）是一种数据类型，它在量化过程中保留了零点，并使用所有$2^k$位来表示k位数据类型。这种数据类型通过估计两个范围的分位数$q^i$来创建一个非对称的数据类型，这两个范围分别是负数部分$[-1,0]$的 $2^{k-1}$和正数部分$[0,1]$的$2^{k-1}+1$。然后，它统一了这两组分位数$q^i$，并从两组中都出现的两个零中移除一个。这种结果数据类型在每个量化bin中都有相等的期望值数量，因此被称为$\text{k-bit NormalFloat}\space (\text{NF}_k)$，这种数据类型对于以零为中心的正态分布数据在信息论上是最优的。

NormalFloat 数据类型是建立在Block-wise k-bit Quantization和分位数量化（Quantile Quantization）基础之上的。

分块k位量化（Block-wise k-bit Quantization）

量化是将数据从一个表示更多信息的形式转换为一个表示较少信息的形式的过程。通常情况下，这涉及将数据类型从一个占用更多比特的形式转换为一个占用较少比特的形式，例如从32位浮点数转换为8位整数。为了确保较少比特的数据类型能够充分利用其范围，通常会对输入数据进行归一化处理，使其适应目标数据类型的范围。例如，将FP32张量量化为范围为[-127, 127]的Int8张量。

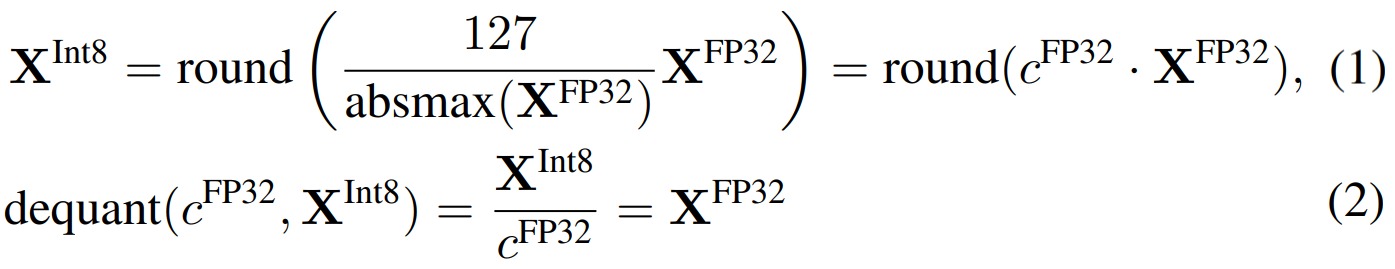
上图是int8量化和反量化。在式(1)中，$\frac{127}{absmax(X^{FP32})}$ 的作用是依据参数中的最大值来确定缩放尺度。这种方法的问题是，如果输入张量中出现较大的幅度值（即异常值），那么使用它计算缩放尺度就不合适了，因为它会造成整个张量的绝大多数值在量化后都在0附近，从而破坏了量化后特征分布的均匀性。分块k位量化（block-wise k-bit quantization）的策略是一批一批的量化：通过将张量分成若干个块，让每个块都有独立的量化常数c，从而解决模型参数的极大极小的异常值的问题。分块量化的另外一个好处是减少了核之间的通信，可以实现更好的并行性，并充分利用硬件的多核的能力。

分位数量化（Quantile Quantization）

QLoRA 是把参数量化到4bit，我们可以使用的数字就是$2^4$ ，即16个。如果采用四舍五入到最近值（RTN, round-to-nearest）方法，则在某些分布下，可能大部分原始数值都被量化到同一个4bit数上，本有的差异或者说信息在这个量化过程中就丢掉了，没有充分利用现有的数位。比如，原始的float32浮点数都在0上下波动，用 RTN 方法，这些数字可能量化完全变成零了。

为了更有效利用现有的16个数字，我们可以采用分位数（Quantile）量化。分位数在数学上的定义指的是把顺序排列的一组数据分割为若干个相等块的分割点的数值。分位数量化是一种信息论上的最优数据类型，其主要思想便是将数值尽量落到均值为0，标准差为[-1,1]的正态分布的固定期望值上。

由于预训练的神经网络权值通常具有标准差为0的正态分布性质，因此我们可以通过缩放系数将所有的神经网络权重转换为固定期望值，从而使该分布完全适合我们的数据类型范围。一旦权重范围和数据类型范围匹配，我们就可以像往常一样进行量化。比如把所有数字由小到大排列，再分成十六等分，最小的一块映射到量化后的第一个数，第二块映射到量化后的第二个数，以此类推。这样做原始数据在量化后的数字上分布就是均匀的。通过使用分位数将张量分成了大小相同的若干个块，我们得到更加均匀的量化特征，这也就是分位数量化。分位数量化技术使得每个量化分区中具有相等的期望值，相等的期望值可以避免昂贵的分位数估计和近似误差，使得精确的分位数估计在计算上可行。

4位正态浮点量化

分位数量化有一个问题：过于繁琐。每一批数字都要计算对应的分位，开销较大。因此，QLoRA 给出了正态浮点量化的加速方法。

预训练的参数基本上是符合均值为0的正态分布的，因此可以直接缩放到指定的范围内，比如 [−1,1] 。对于范围在 [−1,1] 内的零均值正态分布，其标准差为任意 $\delta$ 的信息论上最优数据类型的计算方式如下：

估算理论上的 N(0,1) 分布的 $2^k+1$ 个分位数，以获得 k 位的正态分布量化数据类型；
通过绝对最大值重缩放将输入权重张量规范化到 [−1,1] 范围内来进行量化。此步骤相当于重新缩放权重张量的标准差，以匹配 k 位数据类型的标准差。更具体地，数据类型的 $2^k$ 个值 $q_i$ 的估算方式为：$\begin{equation} q_i=\frac{1}{2}\left(Q_X\left(\frac{i}{2^k+1}\right)+Q_X\left(\frac{i+1}{2^k+1}\right)\right) \end{equation}$ ，其中 $Q_X(\\cdot)$ 是标准正态分布 N(0,1) 的分位数函数。
这样的做法存在一个缺点，0可能会被映射到一个不为零的数值上，损失了0的特殊性质。为了解决这点，QLoRA用两个$2^{k-1}$的[0, 1]范围分别代表正负0~1，再去掉重叠的一个0值。

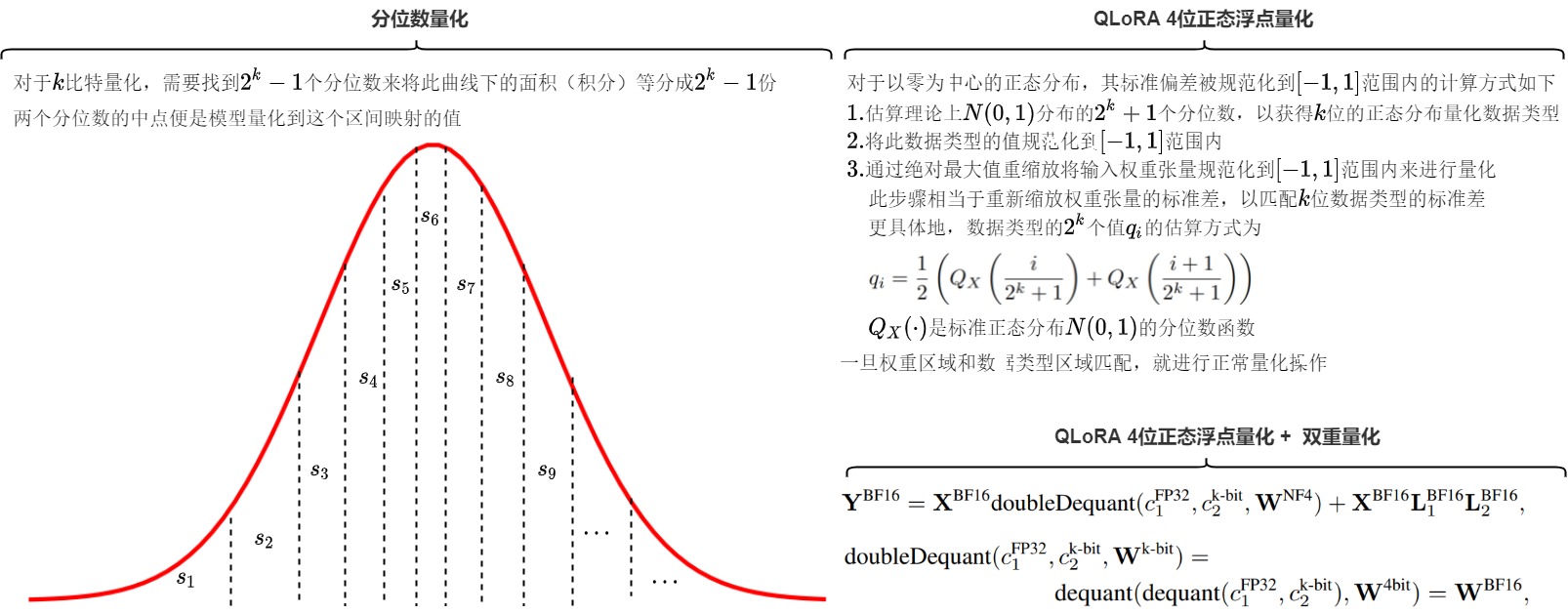
如下图所示，对于4比特量化，我们希望需要找到15个分位数来将这个曲线下面的面积（积分）等分成16份。两个分位数的中点便是模型量化到这个区间映射的值$q_i$。

双重量化

在量化的过程中，为了降低Outlier的影响，QLoRA采用分块的方式进行进行量化。具体来说就是每64个参数共享一个量化常数(Absmax, 32bit)，相当于每一个参数的量化额外开销为$$32/64 = 0.5 \text{bit}$$。对于4bit量化来说额外的0.5bit相当于多12.5%的显存耗用，总体来说也是比较大的一个开销。

为了进一步优化这个量化开销，QLoRA对其进行二次量化($$\text{Double Quantization}$$)，对量化常数进行进一步的量化。即把第一次32bit量化的输出作为第二次量化的输入。考虑到c一般出现outliner的概率较小，LoRA采用256的块大小对量化常数进行$$\text{FP8}$$量化，平均来说，对于64的块大小，这种量化方法将每个参数的内存占用从 32/64=0.5 位降低到 $\begin{equation} 8/64 + 32/(64 * 256) = 0.127 bit \end{equation}$，每个参数减少了0.373位的内存占用。因为使用了双重量化，在进行反量化时，我们也需要进行两次反量化才能把量化后的值还原。

优化器状态分配分页内存

梯度检查点（Gradient Checkpointing）是用于解决模型训练时显存占用过高的问题的一个技术方案。在模型训练时，我们通常需要将所有前向传播的激活值保存下来以在模型进行反向传播的时候使用，但是这样就会非常占用模型显存。当然我们也可以不保存激活值，而是在计算梯度时重新计算，但是这样虽然减少了缓存占用，但是却增大了计算量，减慢了训练速度。

梯度检查点就是一个介于全不丢和全丢弃的一个这种的技术方案，即只在前向传播过程中保存部分激活值。当运行反向过程时，如果有保存的梯度，我们就直接使用这个保存的值，没有保存的梯度时，我们再根据它损失函数重新计算这个梯度。

分页优化是针对梯度检查点做的进一步优化，以防止在显存使用峰值时发生显存OOM的问题。QLoRA分页优化其实就是当显存不足时，这些梯度检查点状态会自动被逐出到CPU RAM，然后在优化器更新步骤中需要内存时，再分页回GPU内存，和计算机的内存数据转移到硬盘上的常规内存分页一个道理。

2.5 FlatQuant

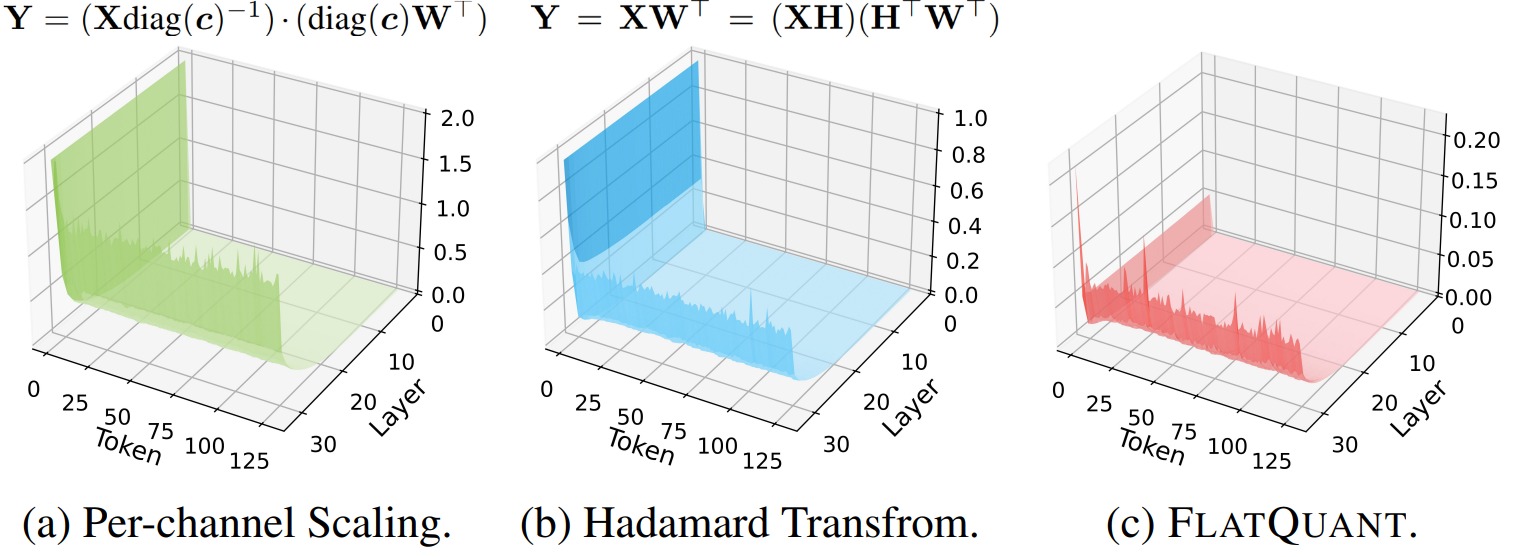
目前的 W4A4 （权重4位，激活值4位）量化模型相比全精度模型还存在着较大的量化损失，难以在实际应用中使用，也就难以利用峰值算力最高的 INT4 Tensor Core 加速 LLM 的实际推理部署。FlatQuant作者发现，量化前权重和激活值分布的平坦度 (flatness) 是影响 LLM 量化误差的关键因素。

直观来看，分布越平坦，离群值就越少，量化时的精度也就越高。已有方法大多使用 pre-quantization transformations，通过在量化前对权重和激活值做等价变换得到更平坦的分布来降低量化误差，常用的变换主要有 Per-channel Scaling 和 Hadamard 变换。

然而，FlatQuant作者发现这些变换并不是最优的，这些变换后的权重和激活值仍然可能保持陡峭和分散。为此FlatQuant作者提出 FlatQuant (Fast and Learnable Affine Transformation)，其目标是通过一些等价变换使得权重和激活值的分布尽量的平坦。具体而言，就是为每个线性层学习一个最优的仿射变换来有效缓解权重和激活值上的离群值，，这组仿射变换矩阵的值是通过校准数据调校训练而来的。从而得到平坦的权重和激活值分布，有效提升了量化精度。此外，针对推理中的在线变换，FlatQuant作者进行了算子融合进一步降低访存开销，使得在线变换仅带来极小的推理开销。

2.5.1 动机

LLM 的权重和激活值上存在较多的离群值，特别是激活值上常常存在离群值通道 (outlier channels)，导致 LLM 难以量化。目前针对 LLM WA 量化的方法大多在量化前对权重和激活值做等价变换来用其他通道吸收离群值，从而得到更加平坦的分布以降低量化损失。例如：

Per-channel Scaling 对应的等价变换为 $\mathbf{Y}= (\mathbf{X}diag(\mathbf{c})^{-1}) \cdot (diag(\mathbf{c}) \mathbf{W}^{\top})$，通过 scaling 将激活值上的离群值转移到权重的相同通道上，使得激活值分布更加平坦；
Hadamard 变换 $\mathbf{Y} = \mathbf{X}\mathbf{W}^{\top} = (\mathbf{XH})(\mathbf{H}^{\top}\mathbf{W}^{\top} , \mathbf{H}^{\top}\mathbf{H} = \mathbf{I}$则是通过给权重和激活值同时做 Hadamard 变换来将离群值重新分配到权重/激活值的其他通道上。

然而，已有的等价变换得到的分布仍然可能是不平坦的。权重和激活值分布可以看作两个斜坡，变换就类似于用铲子搬土，土不会凭空增加或者减少，所以目标是通过把两个坡中高处（离群值）的土填到低处（非离群值通道），从而把这两个坡填平。

Per-channel Scaling 就相当于只能把一个坡上的土填到另一个坡的相同位置上，比较局限。离群值仍然被限制在了权重和激活值的相同通道上，非离群值通道得不到有效利用。因此不管是权重还是激活值，变换后的分布都非常陡峭，呈现出非常明显的离群值通道。
Hadamard 变换相当于在每个坡的内部把高处的土填到自身的低处，但不能在两个坡之间转移土。并且由于不同坡的形状不同，相同的 Hadamard 变换（坡内搬土方式）不一定适用于所有土坡。Hadamard 变换对所有权重和激活值都施加相同的变换，而不同层的权重和激活值分布是不同的，这意味着 Hadamard 变换并不是对于每个层的最优解，例如下图 (b) 中，LLaMA-3-8B 的权重和激活值经过 Hadamard 变换后仍然比较陡峭，特别是激活值上的离群值无法得到有效平滑。此外，Hadamard 变换作为一种正交变换不会改变向量的模长，而 LLM 激活值上大量的离群值会导致激活值模长显著大于权重，这导致正交变换后的激活值量化难度也会显著高于权重，无法像 Per-channel Scaling 一样灵活地平衡权重和激活值上的量化难度。

具有 massive outlier 的关键词元 (pivot token)对于模型性能十分重要，关键词元上的量化误差会比较严重地影响模型的量化精度。下图展示了在LLaMA-3-8B施加不同变换后，Transformer层和输入序列的量化均方误差（MSE）。可以发现，per-channel scaling 和 Hadamard 变换都无法很好处理具有 massive outlier 的关键词元 (pivot token)，导致在首词元上具有非常大的量化误差。而 FlatQuant 方法的 MSE 更小，因此可以显著降低关键词元上的量化损失，并有效抑制量化误差的逐层传播，带来更加平坦的量化损失平面。

2.5.2 方案

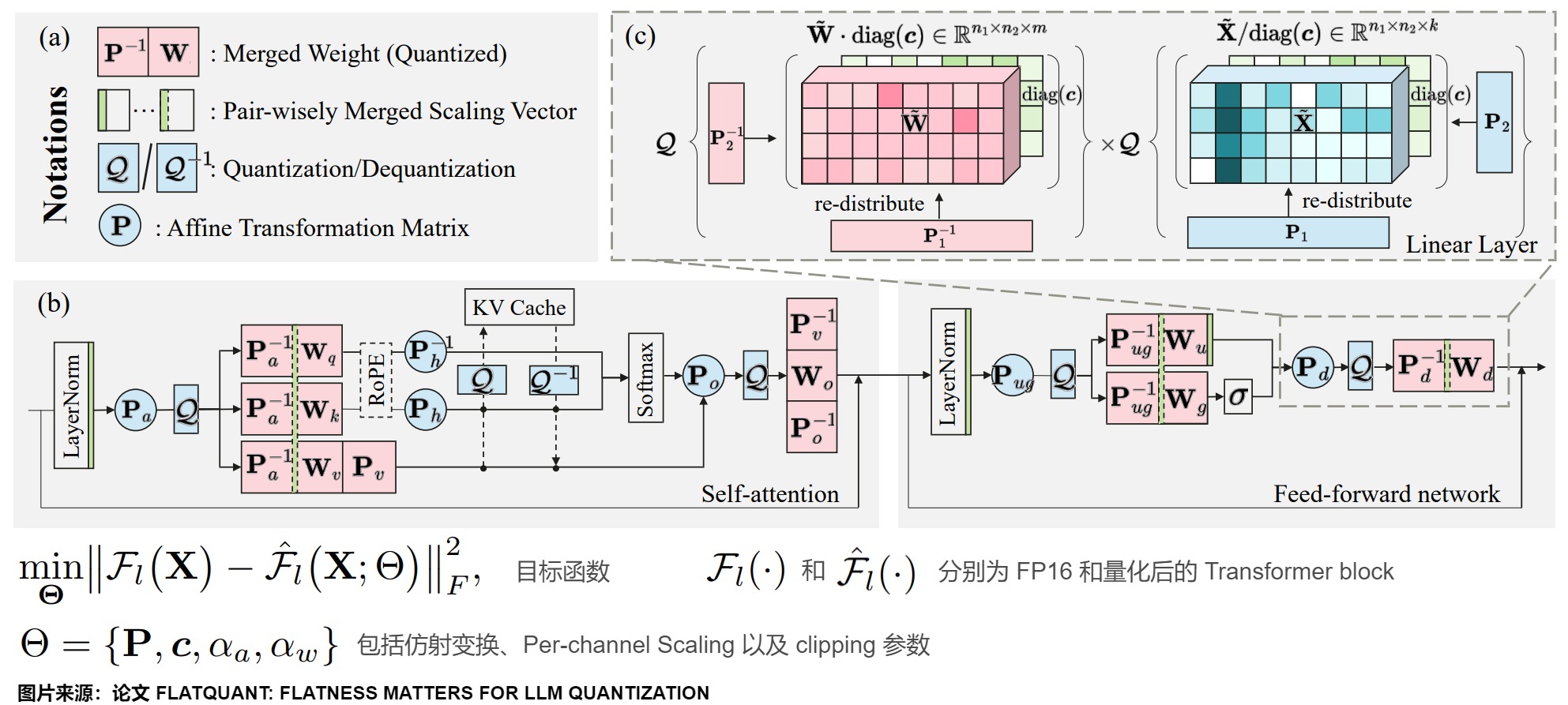
FlatQuant方案关键步骤如下：

轻量仿射变换：通过学习每个线性层的最优仿射变换来平滑离群值。
Kronecker 分解：将大的变换矩阵分解为小矩阵，减少存储和计算开销。
Per-channel Scaling：为每个通道提供独立的缩放因子，增加变换的灵活性。
Learnable Clipping Thresholds：通过可学习的裁剪阈值进一步减少离群值的影响。

相比于Per-channel Scaling和Hadamard 变换，FlatQuant 方法可以被看作是一种更加精细和智能的"搬土"策略。在这个方法中，我们不再局限于只在单个斜坡内部移动土，也不只是在两个斜坡的相同位置上进行土的转移。FlatQuant 允许我们对每个斜坡进行定制化的调整，这意味着我们可以针对每个斜坡的独特形状和需求，设计出最佳的"搬土"方案。这就相当于为模型的每一层学习一个特定的仿射变换，不仅可以得到平坦的分布，还可以自适应地平衡权重和激活值的量化难度。

轻量的仿射变换

FlatQuant 通过轻量的仿射变换来平滑权重和激活值上的离群值，需要为每个线性层学习最优的仿射变换。学到可逆矩阵P后，变换$P^{-1}W^T$可以融到权重中不会带来额外推理开销，但XP必须作为在线变换，这会使得线性层的存储和计算开销翻倍，这显然是不现实的。因此，为了解决上述问题，FlatQuant 对P使用 Kronecker 分解。具体推导如下。

Per-channel Scaling

Kronecker 分解本质上还是对P的 rank-1 近似，我们进一步使用 learnable Per-channel Scaling 提升 Kronecker 分解的表征能力。Per-channel Scaling 可以融到前序的 LN/线性层中不会带来额外推理开销。

Learnable Clipping Thresholds

我们对变换后的权重和激活值进一步采用了 learnable clipping 来更好地消除离群值。

模型架构

下图展示了模型架构，FlatQuant 在单个 Transformer 内会引入 5 种不同的在线变换。损失函数采用 Layer-wise MSE loss。

0x03 低位量化

将量化位数降低到低于8位已被证明是一项艰巨的任务，因为每减少一位，量化误差都会增加。但是内存和运算速度的压力迫使研究人员绞尽脑汁继续探究。于是就有了低位量化方案。

本节介绍的几种方案特点如下。

方法	量化权重与激活	特点
SqueezeLLM	W3~W4/A16	先把极端值分离出来，对剩余的权重用加权的k-means聚类的非均匀量化方法
SpQR	W3~W4/A16	用分治方法分离出敏感权重，然后对非敏感权重采用二级压缩方法，转化为3bit存储
BitNet	W1	BitNet使用-1或1来表示模型权重的单一位，并且将activation量化成8-bit来执行矩阵乘法。模型其余部分则会维持一个高精度，比如FP16
BitNet b1.58	W1.58	主要将weights的取值从{-1, 1}变为{-1, 0, 1}，这赋予了模型忽略（ignore）特定feature的能力，提升了模型性能
OneBit	W1	提出一种新颖的1bit参数表示方法，和一种基于矩阵分解的有效参数初始化方法，以提高QAT框架的收敛速度

3.1 SqueezeLLM

SqueezeLLM是一个训练后量化框架，它不仅使 lossless 压缩到 ultra-low 精度到 3 位，同时也在相同的内存限制下实现了更高的量化性能。SqueezeLLM提出将离群值存储在全精度稀疏矩阵中，并对剩余权重应用非均匀量化。根据量化灵敏度确定非均匀量化的值，能够提高量化模型的性能。

3.1.1 动机

SqueezeLLM 发现，生成式推理的主要瓶颈在于内存带宽即内存墙，而非算术计算，特别是针对单个批次推理时。既然把权重加载到内存是主要瓶颈，因此最小化内存即可。比如仅仅把权重位宽降低而不对激活量化，即可实现运行加速（相当于把权重加载到内存后，再反量化回FP16，这种方式虽然增加了计算开销但降低了访存开销）。另外，权重存在不同敏感度，少量权重非常敏感，需要针对性进行量化。

3.1.2 方案

SqueezeLLM 主要贡献有如下两点：

基于敏感性的非均匀量化。权重分布是不均匀的，使用非均匀量化可以实现3比特量化。
- 它采用近似的Fisher information来度量敏感度，这是一种新的度量方式。然后基于敏感度进行低比特非均匀量化，使用kmeans聚类来生成靠近敏感值的量化定点，其它点以MSE最小来安置，从而最小化量化误差。
稠密和稀疏分解，针对离群点的稠密和稀疏量化：把权重分为稠密和稀疏，稀疏权重不量化，只量化稠密权重。高效的稀疏格式来存储outlier和敏感权重(FP16)，稠密格式来存储大量的低比特常规权重值。分别开发了kernel来处理稠密和稀疏的矩阵向量乘kernel。

基于敏感度的非均匀量化

均匀量化的主要优势是计算高效，但在LLM推理中，计算不是主要瓶颈，并且权重本身是非均匀分布的。因此，作者提出非均匀量化的方式缩小这些敏感权重的量化误差。即通过loss的二阶hessian信息来确定量化敏感的权重, 将量化点安置在这些敏感权重附近。具体推导如下图所示。其中核心点是：

在3bit的时候，只有8个量化slot，因此需要谨慎选择量化值。一种常见的思路就是用k-mean聚类，这里的关键是损失函数的定义。作者尝试用task loss，而不是简化版的单层重建误差。
这里的H求解还是太贵了，作者使用了费舍尔信息矩阵(FIM, fisher information matrix)矩阵来替换，具体来说就是计算一阶梯度的协方差。
因此对于每个$Q(w_i)$，可以使用k-means算法（3比特的时候k=8）来最小化上面的$L(W_Q)$损失误差，最终得到k个离散的一维浮点值。

针对离群点的稠密稀疏量化

作者分析了一下MHA的输出proj矩阵和FFN的contraction矩阵的权重分布，如下所示，发现

99.9%的权重挤在最大区间的10%以内的地方。
剩下0.1%的权重在最大区间的10%-90%的地方，属于outlier。

这表明去除离群点可以将量化阈值缩小10倍。

因此，作者采用了简单而有效的分解思路，如下图所示，把权重W分解成容纳异常值权重的稀疏矩阵(S)和包含剩余的大多数权重的稠密矩阵(D)。前者保持FP16后者量化。SqueezeLLM 通过迭代过程将权重矩阵分解为一个稀疏矩阵和一个密集矩阵，分解成稀疏矩阵的过程中实现了压缩和量化。另外，除了把离群点放入稀疏矩阵，还可以根据Fisher信息度量把小部分敏感权重也放入稀疏矩阵。

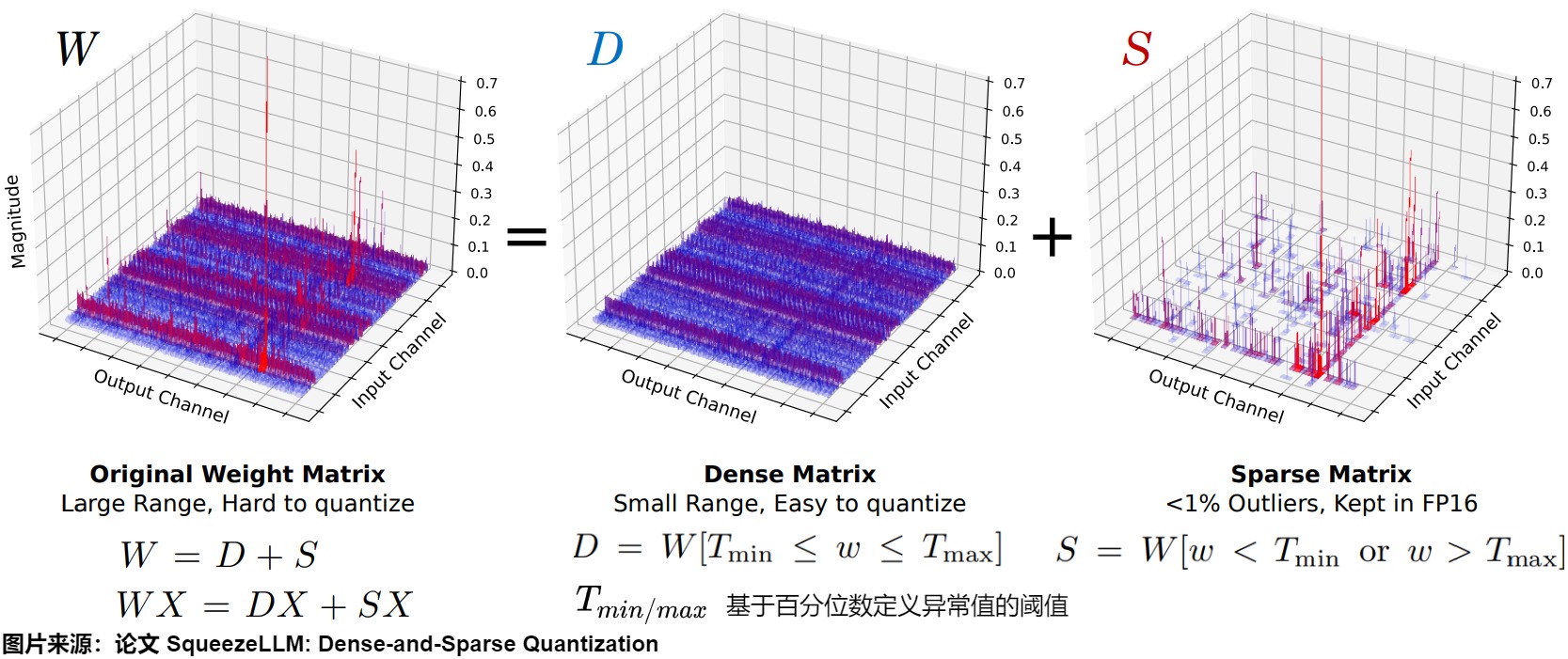
这里，$T_{min/max}$是基于百分位数定义异常值的阈值。

重要的是，因为异常值的数量很小。因此，可以使用高效的稀疏格式来存储outlier和敏感权重(FP16)，使用稠密格式来存储大量的低比特常规权重值。

3.2 SpQR

论文"SpQR: A Sparse-Quantized Representation for Near-Lossless LLM Weight Compression"提出了SpQR。SpQR也像AWQ一样发现了weight对模型的重要程度存在极强的不均衡性，1%的参数可能主导的量化过程中损失的性能这一事实。但是它对识别敏感weight和保护敏感weight的做法和AWQ不一样，其工作原理是识别和单独处理会导致大量化误差的异常值权重，并以更高的精度存储它们，同时将所有其他权重压缩到 3-4 比特。

3.2.1 动机

随着大模型的参数越来越大，通常需要通过量化将此类LLMs压缩为每个参数3-4比特，以适合笔记本电脑和移动电话等内存有限的设备，从而实现个性化使用。但现有的技术方案（如：GPTQ）将参数量化至 3-4 比特通常会导致显著的精度损失，特别是对于 1-10B 参数范围内的较小模型，而这些模型却非常适合边缘部署。为了解决这个精度的问题，作者引入了稀疏量化表示（SpQR），这是一种新的压缩格式和量化技术，首次实现了跨模型参数规模的近乎无损的（near-lossless） LLM 压缩，同时达到与以前的方法类似的压缩水平。

离群值

早期的工作[LLM.int8()、Smoothquant]观察到在大语言模型的输入/输出中存在显著较高值的"离群特征"，这会导致更高的量化误差，并提出不同的缓解策略。而本文的作者从权重量化的角度来分析这个现象。特别是，作者研究了除权重矩阵中的输入特征离群值之外的离群值结构。结果发现，虽然当前层的输入特征异常值与前一层的隐藏单元异常值权重相关，但并不存在严格的对应关系。论文首次证明，与输入特征异常值不同，输出隐藏维度异常值（output hidden dimension outliers）仅出现在特定输出隐藏维度的小片段中（small segments for a particular output hidden dimension）。这种部分结构化的异常值模式需要一种细粒度的混合压缩格式。

针对离群值特点，SpQR 作者提出的量化算法隔离此类异常值，并以 SpQR 格式有效地对给定模型进行编码。

参数灵敏度分析

首先它用类似OBC(Optimal Brain Compression)的方式来计算参数的敏感度，求解结果如下所示。

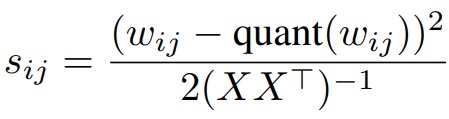
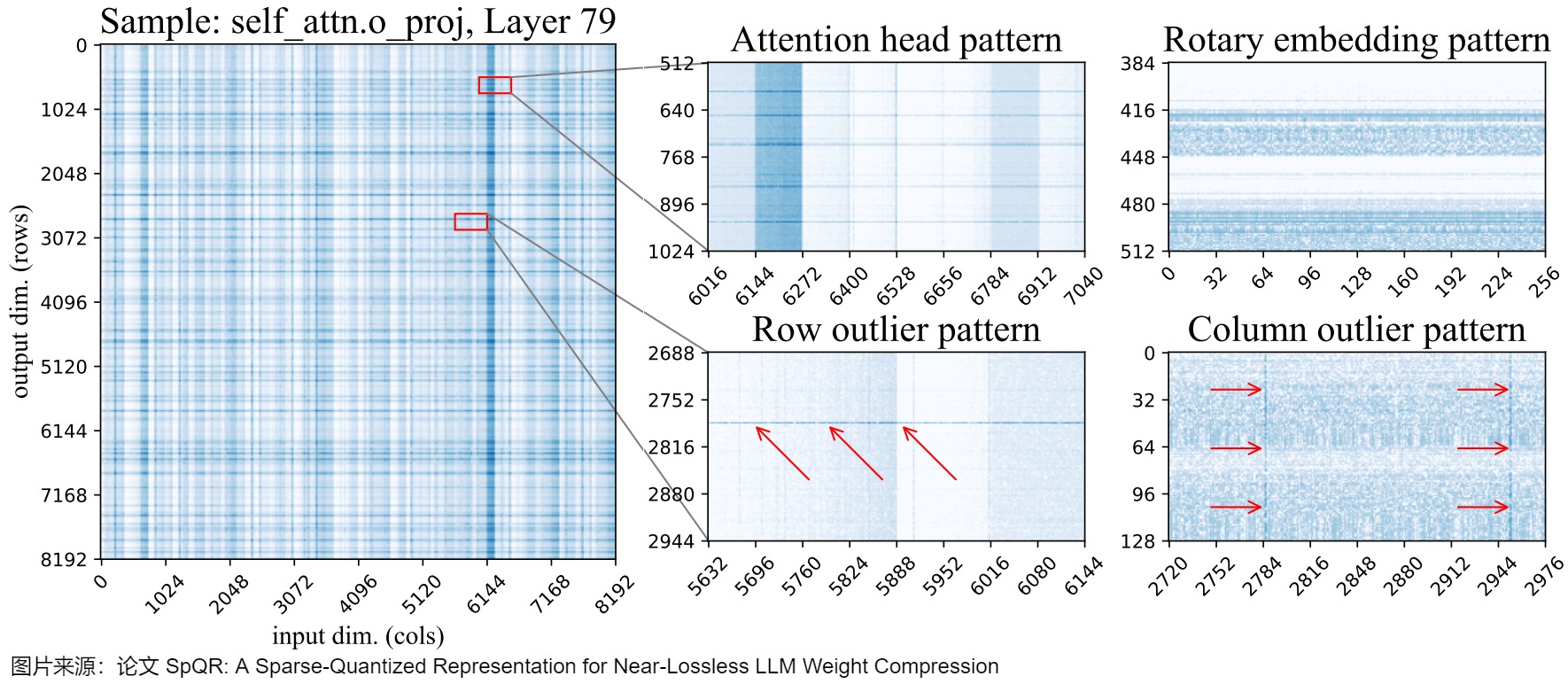
其次，论文对权重的参数敏感度进行了分析，结果发现，敏感权重在权重矩阵中的位置不是随机的，而是具有特定结构（行、列、注意力头、非结构化等）。下图展示了LLaMA-65B最后一个自注意力层的权重对数敏感度（log-sensitivities）。深蓝色阴影表示敏感度较高。通过敏感度分析，作者观察到在权重矩阵中存在的几种模式：

行异常值：图底部中心对应于输出特征的高敏感度区域。其中一些模式横跨整行，而另一些模式则占据了行的部分。在注意力层中，一些部分行异常值对应于注意力头的某个子集。
列异常值：图右下角底部显示了跨越所有行（across all rows）的选择输入维度（列）的高灵敏度。
敏感注意力头：图顶部中心区域出现了宽度为 128 的规则条纹，这对应了一个注意力头的所有权重。这些的"条纹"在 Q & K 投影矩阵中是水平形状，在输出投影矩阵中是垂直形状，但是在 V 投影矩阵和任何 MLP 权重中都没有出现。值得注意的是，即使在敏感的头（sensitive heads）内，单独的权重敏感性也存在显著差异。
旋转嵌入模式：图右上角所展示了 64 个单位周期的重复垂直敏感度模式，这是旋转嵌入位置编码的特有模式。任何不使用旋转嵌入的层都没有这种模式。
非结构化异常值：除此之外，每一层都有许多单独的敏感度权重，这些权重不适合任何上述模式。这些非结构化异常值更频繁地出现在具有最大输入索引的列中（即在图像的右侧）。但在热力图上很难看到这种效果。

因此，作者希望使用一个压缩方案来维持所有这些不同的离群值类型。

3.2.2 方案

针对离群值，作者提出用量化算法隔离此类异常值（敏感值group和单个异常值），然后将它们存储在更高的精度中；将所有其他权重压缩为3-4比特。并以 SpQR 格式有效地对给定模型进行编码。

量化算法

之前的 LLM 量化算法同等对待低敏感度权重和高敏感度权重，这可能会导致次优量化。理想情况下，我们应该为更高敏感度的权重分配更多的存储资源（size budge）。然而，这些权重多为非结构化异常（单独权重)或形成小组分散在权重矩阵中，例如：部分行或注意力头。为了捕捉这种结构，本文将量化过程分为两部分：捕捉小的异常组；捕获单个异常值。

通过双层（bilevel）量化捕获小组（small groups ）权重

在上图中，我们观察到了在几种模式中，权重在连续的小组中表现相似，但组之间发生突然变化。例如：某些注意力头和部分行异常值。当应用标准方法时，在很多情况下，这些权重将被分组在一起，共享相同的量化统计数据。为了减少此类情况，我们使用极小的组进行分组量化，通常为 β1=8~32 个权重。也就是说，对于每 β 个连续权重，都有一个单独的量化 scale 和 zero-point。

为了避免"存储量化统计数据的开销抵消精度优势"，我们使用与权重相同的量化算法------非对称（最小-最大）量化来量化分组统计数据本身。换句话说，我们对来自 β2=16 个连续值的分组统计数据进行分组，并以相同的位数将它们一起量化，这样具有非典型量化参数的组最终会使用更多的"量化预算"。

高灵敏度异常值

事实上，存在一小部分敏感权重以小组形式（在 Self Attention 层）或单独"异常值"形式（在 MLP 中）出现的情况。这些异常权重往往只占全部权重的 1%，但却会导致占据总体 75% 以上的量化误差。由于这些离群值通常是非结构化的，因此本文选择将这些异常值保持在高精度（16 位），并以类似于压缩稀疏行（CSR）表示 [5]的行排列对它们进行单独编码。

检测高灵敏度异常值的算法如下图所示：左侧片段描述了完整的过程，右侧包含用于bilevel量化和查找异常值的子例程。左侧片段具体如下：

第一步是"异常值检测"步骤：查找异常值，并将其保持为 16 位权重。我们发现量化异常值会导致不成比例的高误差。因此，将这些权重保持高精度。敏感权重的计算参照了OBS里面的结论。这里使用了逐层的重建误差。在全局范围内，对于每个矩阵，该算法的目标是选择一个敏感度阈值 τ 以获得整个模型中所需的异常值数量，通常约为权重的 1%。
第二步是"实际压缩步骤"：将大多数（≥99%）的非异常值权重近似量化为 3~4 比特，并将剩余的量化转移到 16 比特异常值权重中。

在第一个异常值检测步骤之后，SpQR 会忽略同一量化组中的所有异常值，只量化非异常权重。同时，在最小-最大量化后，该算法还会继续应用 GPTQ 来量化剩余权重。最后，该算法通过分级量化对稀疏异常值矩阵以及最终的量化统计量进行收集和压缩，并返回压缩后的权重及其元数据。

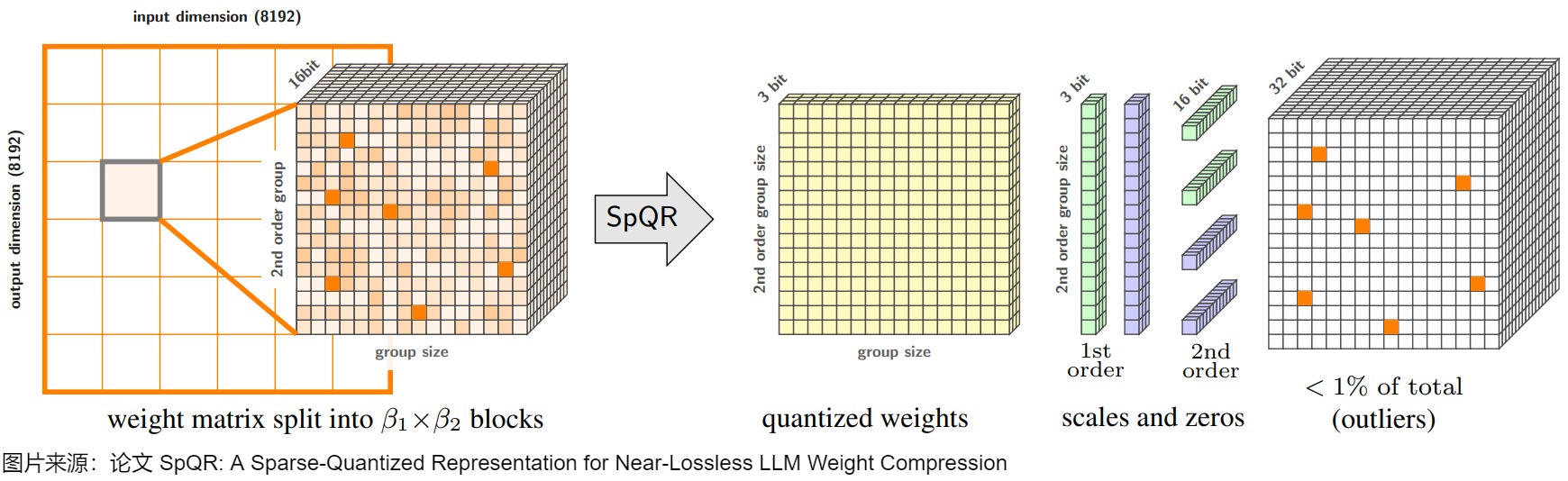
稀疏量化表示的实现和利用

SpQR将均匀权重转换为不同大小和精度的多种数据结构。总体而言，该表示由(1)量化权重、(2)一级量化统计数据、二级量化统计和 (3) CSR 异常值索引和值组成。下图总结了 SpQR 的总体结构。左侧是单个权重张量的 SpQR 表示方法的概述，右侧描绘了所有存储的数据类型及其维度。

下面是每个组件的描述。

存储量化组（Storing quantized groups）。所有非异常值权重都被编码为一个结构，该结构包含：

一个$b_w$-bit的独立权重
每组（组的大小是B）对应的$b_q$-bit的scale 和 zero point（一级量化）
用于量化 $B_q$个量化组（scale 和 zero point）的 16 比特统计数据（二级量化）

存储异常值（Storing outliers）。由于异常值是非结构化的，SpQR 按照它们的行和列对它们进行排序，这样同一行中的异常值在内存中是连续的。对于每个异常值，本文存储两个标量：16 位权重值和 16 位列索引。对于每一行，还存储一个 32 位的数字，用于表示行中异常值的总数。每个异常权重的平均存储成本为 32.03 至 32.1 比特。

3.3 BitNet

BitNet使用**-1** 或1来表示模型权重的单一位，即将weight matrix量化成1-bit（即取值1或-1），并且将activation量化成8-bit来执行矩阵乘法。然后使用1-bit矩阵乘上8-bit activation的矩阵运算，代替一般神经网络中的矩阵乘法nn.Linear。模型其余部分则会维持一个高精度，比如FP16，包括梯度、优化器状态、以及Attention里的运算。

3.3.1 方案

架构

BitNet将量化过程直接注入到Transformer 架构中。Transformer 架构是大多数LLM的基础，该架构在计算中严重依赖线性层。这些线性层通常以更高的精度（例如FP16）表示，模型的大部分权重都存在于此。因此，BitNet对此进行了修改，引入了BitLinear层来替换这些线性层。

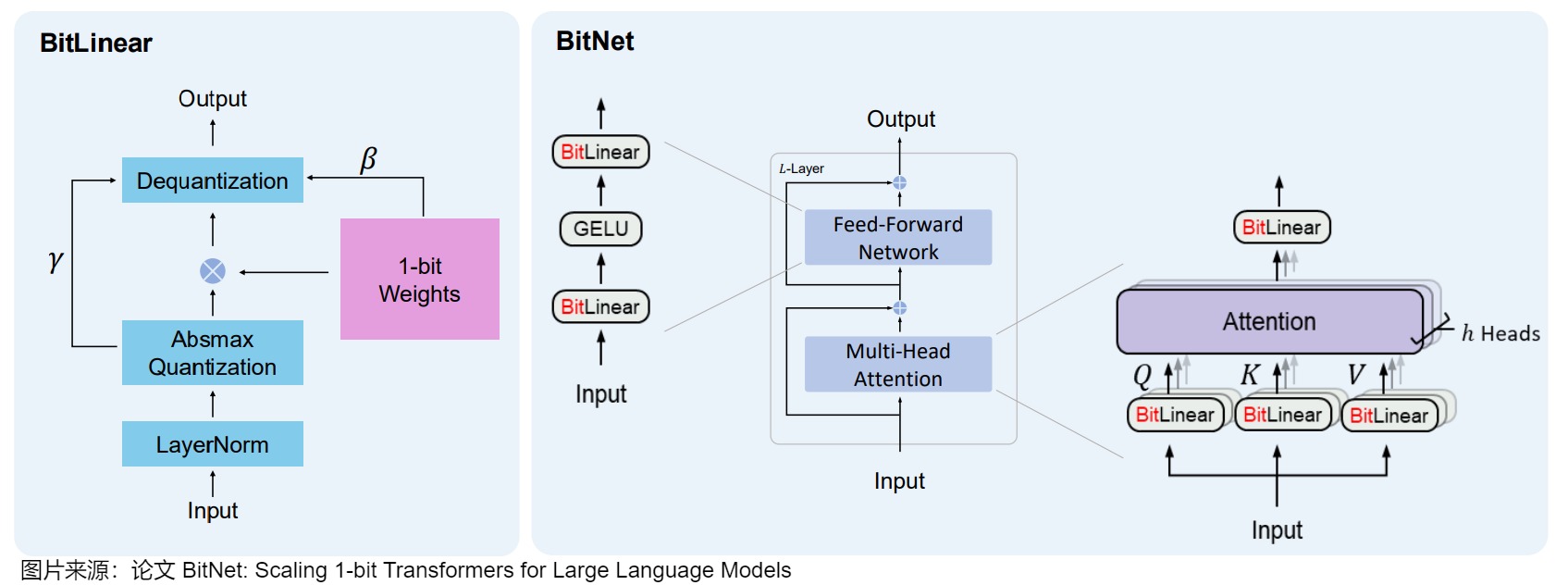
BitLinear层的工作方式与普通线性层相同，根据权重乘以激活来计算输出。但是BitLinear层使用1位来表示模型的权重，并使用INT8来表示激活。这种方法显著减少了模型的存储和计算需求，使得在资源受限的环境中部署大型语言模型变得可行。同时，通过这种极端的量化方法，BitNet在维持性能的同时大幅降低了能耗和运行成本。

另一方面，作者希望维持梯度更新操作的高精度，因此还会在训练过程中维持一个高精度的隐含的权重矩阵（当然在计算的时候会进行1-bit量化，只是在更新参数的时候是高精度的），另一方面作者认为Transformer计算的主要workload在于矩阵乘法，因此优化nn.Linear操作最为重要。

流程

BitLinear在训练时的流程如下。

一开始有一个高精度的input activation，一个高精度的weight matrix。
用零初始化weight，然后用一个sign函数将它转变成1-bit（1或-1）。
用LayerNorm归一化input，然后做8-bit quantization。
用1-bit weight乘上这个8-bit input，得到8-bit的output。
用之前量化的参数做dequantization，得到高精度的output。

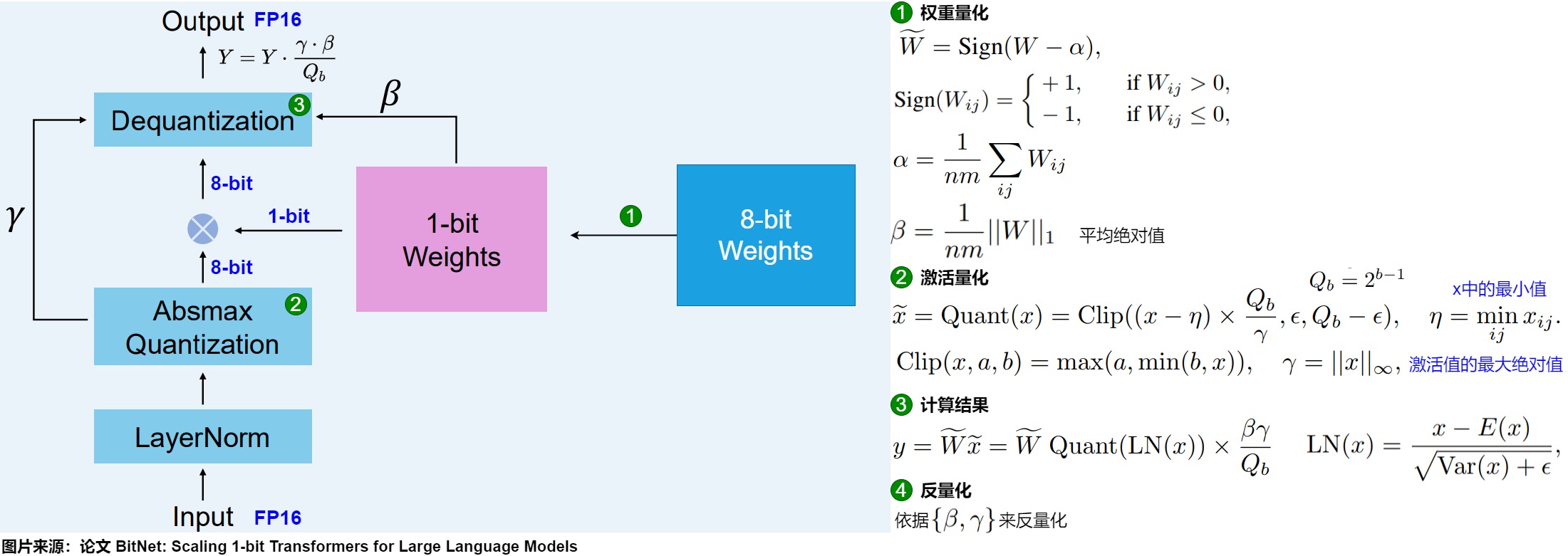
权重量化

在训练过程中，权重存储在INT8中，然后使用一种称为符号函数的基本策略，将其量化为1位。具体而言，它将权重的分布移动到以0为中心，然后将0左边的所有值赋值为-1，右边的所有值赋值为1。

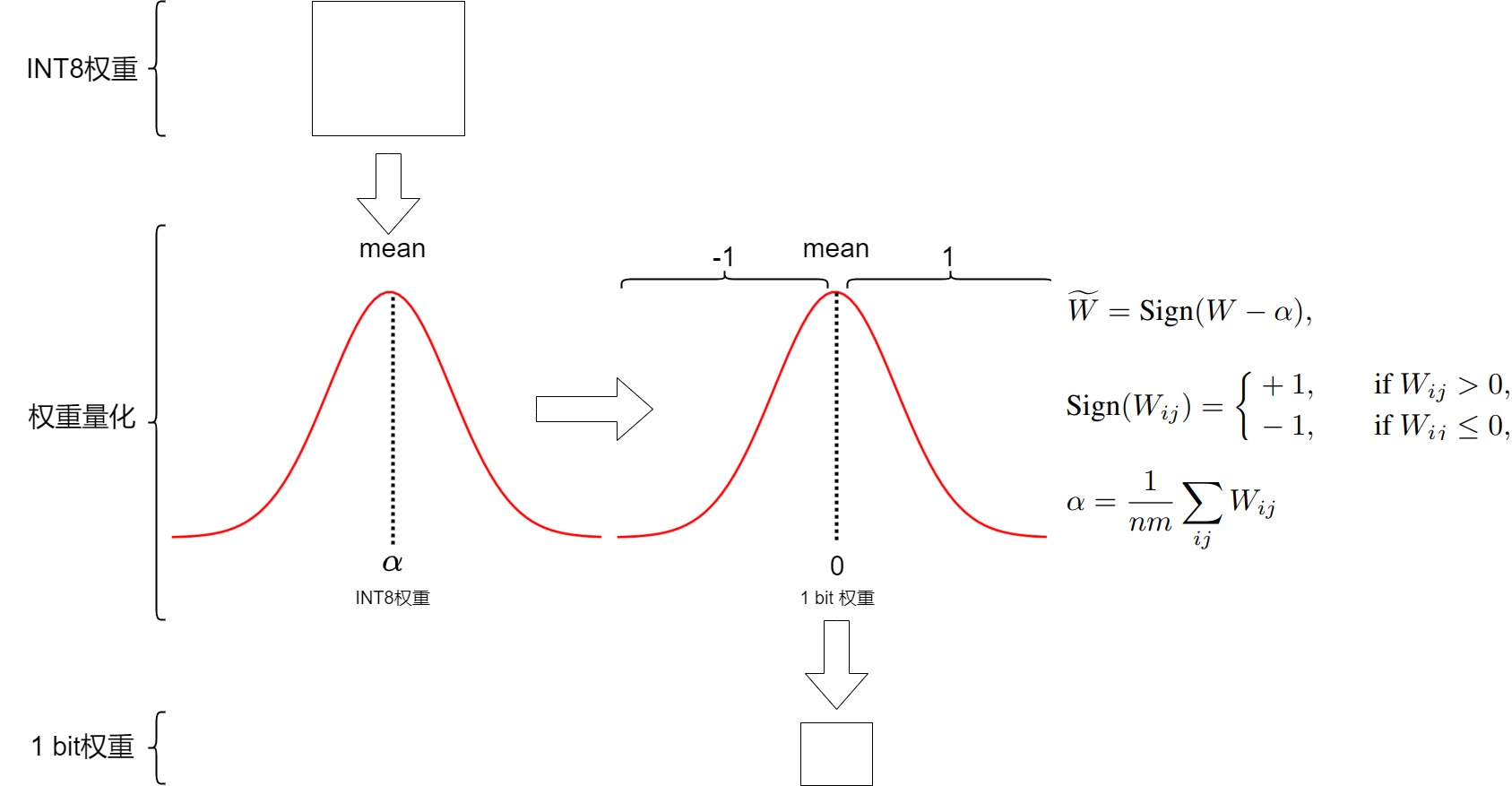
此外，它还跟踪一个值 β（平均绝对值），因为稍后将用它进行去量化。

激活量化

为了量化激活值，BitLinear使用absmax（绝对最大）量化将激活值从FP16转换为INT8，因为在矩阵乘法中它们需要更高的精度。此外，它还记录了激活值的最高绝对值α，因为稍后将用它进行去量化。

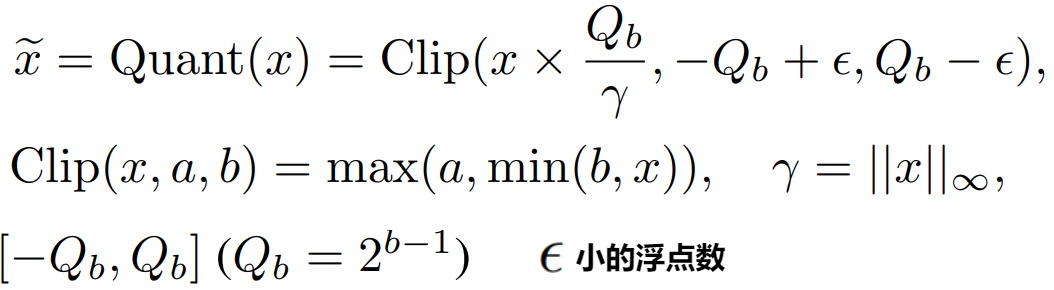
反量化

上面跟踪了 α（激活值的最大绝对值） 和 β（权重的平均绝对值） ，这些值将帮助我们将激活值反量化回FP16。输出激活值使用 {α, γ} 重新缩放，以将其反量化到原始精度：

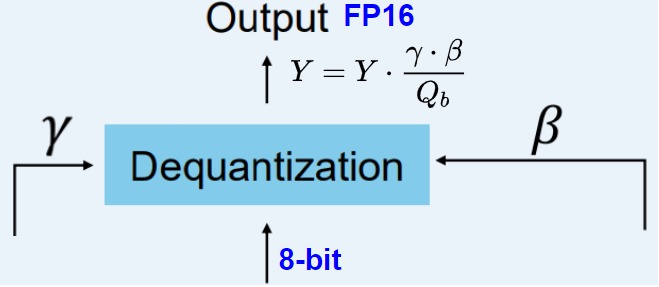
QAT

BitLinear层像QAT那样，在训练期间执行一种"假"量化形式，以分析权重和激活量化的效果。

反向传播的时候会遇到quantization和sign操作无法传递梯度的问题，论文用STE (straight-through estimator) 将梯度直接传递回去。在Inference的时候是不需要维持一个高精度的weights的，直接用1-bit量化版本即可。同时论文发现1-bit模型在训练时比高精度模型更稳定，而且由于weight不是1就是-1，如果gradient太小，一步更新后模型可能没有什么变化，因此论文推荐使用更大的学习率。

3.3.2 结果

BitNet体现出了良好的scaling law，即通过小参数模型的训练loss和参数量，可以准确地预测更大参数量模型的训练结果，而且与FP16精度模型的差距随着参数量增大而减少。同时由于使用1-bit weights，原先nn.Linear中的矩阵乘法如今只要做加法就可以了，乘法主要是在scaling的时候用一下，使得计算量大减。

BitNet和Post-training quantization主要区别在于BitNet需要从头训练模型，这确实是一些劣势，但在推理阶段的优势非常明显，拥有极低的显存占用和计算量。

3.4 BitNet b1.58

BitNet b1.58 是 BitNet 的一个改良版本，主要将weights的取值从{-1, 1}变为{-1, 0, 1}，这也是为什么说这个模型是1.58-bit的原因，这赋予了模型忽略（ignore）特定feature的能力，提升了模型性能，并且增加一个0的选择，进行矩阵乘法时也还是只需要进行加法即可。

3.4.1 方案

1.58位量化主要需要两个技巧：

添加 0 创建三元表示 [-1, 0, 1]。
absmean 量化用于权重。

这样就得到了轻量级模型，因为它们只需要1.58位的计算效率。

0的力量

添加 0 的作用是可以消除一次乘法操作。所以如果权重量化到1.58位，只需要进行加法操作。

矩阵乘法在计算输出时，将一个权重矩阵乘以一个输入向量。这种乘法涉及两个动作，即乘输入和单个权重，然后将它们加在一起。

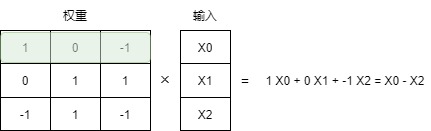
BitNet 1.58b 通过使用三元权重基本上可以避免乘法操作，因为三元权重本质上告诉你以下信息：

1 --- 我想添加这个值
0 --- 我不需要这个值
-1 --- 我想减去这个值

通过将给定的权重设置为0，就可以忽略它，而不是像1位表示那样要么添加要么减去权重。这不仅可以显著加速计算，还允许进行特征过滤。

量化

为了进行权重量化，BitNet 1.58b 使用了 absmean 量化（绝对均值量化）。它简单地压缩权重的分布，并使用绝对平均值（α）来量化值，即将权重分布压缩在绝对均值（α）附近。然后这些值被四舍五入为 -1、0 或 1。与BitNet相比，激活量化基本相同，但是激活不再缩放到范围 [0, 2ᵇ⁻¹]，而是使用 absmax 量化缩放到 [-2ᵇ⁻¹, 2ᵇ⁻¹]。

3.5 OneBit

论文"Onebit: Towards extremely low-bit large language models"引入了一个名为OneBit的1bit量化感知训练（QAT，quantization-aware training）框架，包括一种新颖的1bit参数表示方法，和一种基于矩阵分解的有效参数初始化方法，以提高QAT框架的收敛速度。

3.5.1 主要贡献

Onebit的贡献是如下：

提出了一种新颖高效的1-bit模型架构，用于LLMs，它可以在模型推理过程中提高时间和空间效率，架构在量化LLMs时更稳定。
提出了SVID（符号-值独立分解）来将高比特矩阵分解为低比特矩阵，这对于1-bit架构的初始化至关重要。实验表明，基于SVID的初始化可以提高模型性能和收敛速度。

3.5.2 挑战

模型量化的主要思想是将模型中的每个权重矩阵W从FP32或FP16格式压缩成低比特的对应物。具体来说，我们通常将Transformer中线性层的权重矩阵量化为8比特、4比特，甚至2比特。大多数量化研究主要采用四舍五入到最近值（RTN, round-to-nearest）方法，即将权重w四舍五入到量化网格中最接近的值。这可以表示为：

\[\hat w = Clip(\lceil \frac{w}{s}\rfloor +z,0,2^N-1) \]

其中s表示量化比例参数，z表示零点参数，N是量化比特宽度。Clip(·)将结果截断在0到 2^N−1 的范围内。

随着比特宽度越来越低，量化网格也变得更加稀疏。当我们将LLM量化为1bit时，量化模型中只有2个可用数字可供选择。此外，当N等于1时，基于RTN方法的量化本质上等同于设置一个阈值，权重w在它的两侧被转换为相应的整数值 $\hat w$。这种情况下，方程中的参数s和z实际上失去了实际意义。因此，当将权重量化为1比特时，基于元素的RTN操作严重破坏了权重矩阵W的精度，造成了权重矩阵 W 中极低比特宽度下的巨大精度损失，显著增加了LLMs核心操作符线性投影WX 的损失。导致量化模型性能下降。

3.5.3 方案

Onebit在BitNet上改进。

1-bit线性层架构

由于1-bit权重量化的严重精度损失，直接按照RTN将线性层中的权重矩阵从FP32/16格式转换为1-bit格式是难度非常大的。BitNet通过研究纯粹1-bit权重矩阵的能力，从头开始训练1-bit模型，探索了这种可能性。在W1A16设置下，BitNet的线性层被设计如上图左侧。其中 W 表示形状为m×n的量化权重矩阵， W±1 表示1-bit量化矩阵。X是线性层的输入，Y是输出。Sign(·)、Mean(·)和Abs(·)函数分别返回符号矩阵、平均值和绝对值矩阵。不幸的是，这种方法虽然减少了计算需求，但也导致了显著的性能下降。

受到 BitNet 的启发，OneBit 也使用Sign(·)函数量化权重矩阵，并将量化矩阵的元素设置为+1或-1。此外，我们还注意到，尽管 W±1 保持了 W 的高秩，但缺失的浮点精度仍然破坏了模型性能。与以前的工作不同，OneBit 引入了两个FP16格式的值向量来弥补量化过程中的精度损失。OneBit 提出的线性层被设计为：

\[W±1=Sign(W) \\ Y=[(X⊙g)⋅W^T_{±1}]⊙ℎ \\ Z=LayerNorm(Y) \]

其中 g 和 h 是两个FP16值向量。注意在上述公式中使用括号指定了计算顺序，这样可以最小化时间和空间成本。BitNet 和OneBit之间的主要区别在于额外的参数 g 和 h。即使引入了额外的参数，其带来的好处也远远超过了其小成本。例如，当我们量化一个形状为4096×4096的权重矩阵时，量化结果的平均比特宽度为1.0073。

下图给出了OneBit 方法的主要思想。左侧是原始的 FP16 线性层，其中激活值 X 和权重矩阵 W 都采用 FP16 格式。右侧是 OneBit 提出的架构，只有值向量 g 和 h 保持 FP16 格式，而权重矩阵由 ±1 组成。⊗：哈达玛积（Hadamard product）。

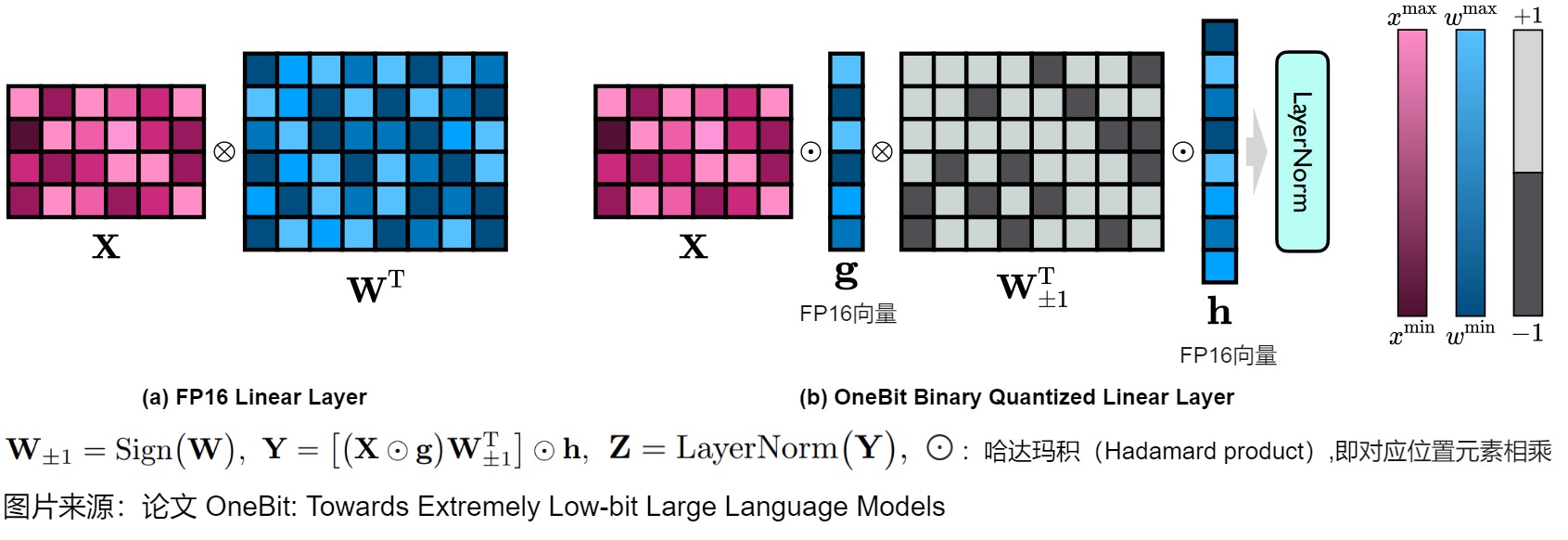
符号-值独立分解（SVID）

在SVID（Sign-Value-Independent Decomposition）中，每个原始的高比特权重矩阵被分解成一个INT1格式的符号矩阵（W±1）和两个FP16值向量g和h。值向量在很小的代价下为线性投影提供了必要的浮点精度，并帮助模型轻松训练。符号矩阵以很小的空间成本保持了原始权重矩阵的高秩，从而保留了高信息容量。

具体推导如下：

知识转移

SVID为1bit模型提供了更好的参数初始化，OneBit采用量化感知的知识蒸馏将原始模型的能力转移到提出的1比特对应物。具体而言，OneBit采用量化感知知识蒸馏，将知识从原始模型（即教师模型）转移到量化模型（即学生模型）。在学生模型中训练矩阵W和向量g/h的元素。使用基于交叉熵的logits和基于均方误差的全精度教师模型隐藏状态来指导量化的学生模型。

0xFF 参考

Onebit: Towards extremely low-bit large language models

https://arxiv.org/pdf/2402.17764

H. Wang, S. Ma, L. Dong, S. Huang, H. Wang, L. Ma, F. Yang, R. Wang, Y. Wu, and F. Wei. BitNet: Scaling 1-bit transformers for large language models. arXiv preprint arXiv:2310.11453, 2023.

Yuzhuang Xu, Xu Han, Zonghan Yang, Shuo Wang, Qingfu Zhu, Zhiyuan Liu, Weidong Liu, and Wanxiang Che. 2024. Onebit: Towards extremely low-bit large language models. CoRR, abs/2402.11295.

Fast and Efficient 2-bit LLM Inference on GPU: 2/4/16-bit in a Weight Matrix with Asynchronous Dequantization

大模型量化技术原理-SpQR 吃果冻不吐果冻皮

SqueezeLLM

LLM 量化新篇章，4-bit 权重激活量化几乎无损！FlatQuant 的平坦之道 NeuralTalk

LLM-QAT: Data-Free Quantization Aware Training for Large Language Models

https://www.armcvai.cn/2024-11-01/llm-quant-awq.html

LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale

https://www.armcvai.cn/2024-10-30/llm-smoothquant.html

https://www.armcvai.cn/2024-10-31/smoothquant-inplement.html

https://www.armcvai.cn/2024-11-03/awq-code.html