机器学习与深度学习16-概率论和统计学01

前文回顾

上一篇文章地址：链接

1.什么是概率论和统计学

概率论和统计学是数学中重要的分支，用于研究随机事件和数据的分布、关联性以及不确定性。概率论是研究随机事件发生的可能性和规律的数学学科。它提供了一套工具和方法来描述和分析随机变量、随机过程以及他们之间的关系。概率论包括概率分布、随机变量、条件概率、期望值等基本概念，并通过概率模型和统计推断来预测和解释随机现象。

统计学是一门研究收集、分析和解释数据以作出推断和决策的学科。统计学涉及数据的收集、汇总、可视化和推理分析，借助概率论中的概念和方法来建立和验证统计模型，并从样本中推断总体的特征和关系。统计学包含描述统计、推断统计、假设检验、回归分析等内容，旨在通过对数据的分析来获得洞察和决策支持。在数据科学和机器学习中，概率论和统计学扮演着重要的角色：

描述和推断数据：概率论和统计学提供了描述和分析数据的方法。概率分布描述了数据的分布特征，统计推断则使用样本数据进行参数估计和假设检验，以推断总体的特征。
建立模型：概率论和统计学提供了建立概率模型的理论基础。通过对数据进行建模，可以从统计角度解释数据的生成过程，并用模型来进行预测、分类、聚类等任务。
评估和优化模型：概率论和统计学提供了评估模型好坏的指标和方法，如最大似然估计、贝叶斯推断等。这些方法能够帮助我们从数据中学习模型的参数，优化模型的性能，并对模型进行比较和选择。
处理不确定性：概率论和统计学处理不确定性的能力使其在机器学习中发挥重要作用。机器学习算法通常面临不完整或噪声数据，概率论和统计学提供了对这些问题进行建模和处理的工具，如贝叶斯网络、高斯过程等。

综上所述，概率论和统计学在数据科学和机器学习中被广泛应用，它们提供了分析数据、建立模型、优化算法以及量化不确定性等方面的基础和方法，帮助我们从数据中提取知识、做出决策并解决实际问题

2.概率的基本概念

事件（Event）：事件是指可能发生或不发生的结果或现象。在概率论中，事件可以是单个结果，也可以是一组相关的结果。例如，掷一个骰子，事件可以是骰子落在特定数字上的结果，或者是骰子落在奇数的结果
样本空间（Sample Space）：样本空间是指所有可能结果的集合。它代表了一个试验或随机现象的所有可能结果。使用大写字母S来表示样本空间。例如，对于一个掷骰子的试验，样本空间可以是{1, 2, 3, 4, 5, 6}
概率分布（Probability Distribution）：概率分布描述了随机变量取不同值的概率。随机变量可以是离散的（只能取某些特定值）或连续的（可以取任意值）。概率分布可以用函数、图表或表格来表示。常见的概率分布包括离散分布（如二项分布、泊松分布）和连续分布（如正态分布、指数分布）
随机变量（Random Variable）：随机变量是定义在样本空间上的变量，它的取值由试验结果决定。随机变量可以是离散的或连续的，并且可以有不同的概率分布。离散随机变量只能取特定的值，而连续随机变量可以在一定范围内取任意值
随机变量可以分为两种类型：

离散随机变量：它只能取一些特定的值，例如投掷硬币的结果（正面或反面）、骰子的点数等
连续随机变量：它可以在一定范围内取任意值，例如身高、温度等。连续随机变量通常由概率密度函数（Probability Density Function, PDF）来描述其概率分布

以上是关于概率的基本概念的详细解释。这些概念是概率论的基础，用于描述和分析随机事件和现象，并为建立概率模型和进行统计推断提供了理论基础

3.什么是概率密度函数和累积分布函数

概率密度函数（Probability Density Function，PDF）和累积分布函数（Cumulative Distribution Function, CDF）是描述概率分布的两个重要概念。概率密度函数（PDF）：对于连续随机变量，概率密度函数（PDF）描述了随机变量取某个值的概率密度。它用于定义在给定值附近的概率分布。对于一个随机变量X，其概率密度函数可表示为f(x)。对于任意给定的x，f(x)表示在x附近取值的概率密度

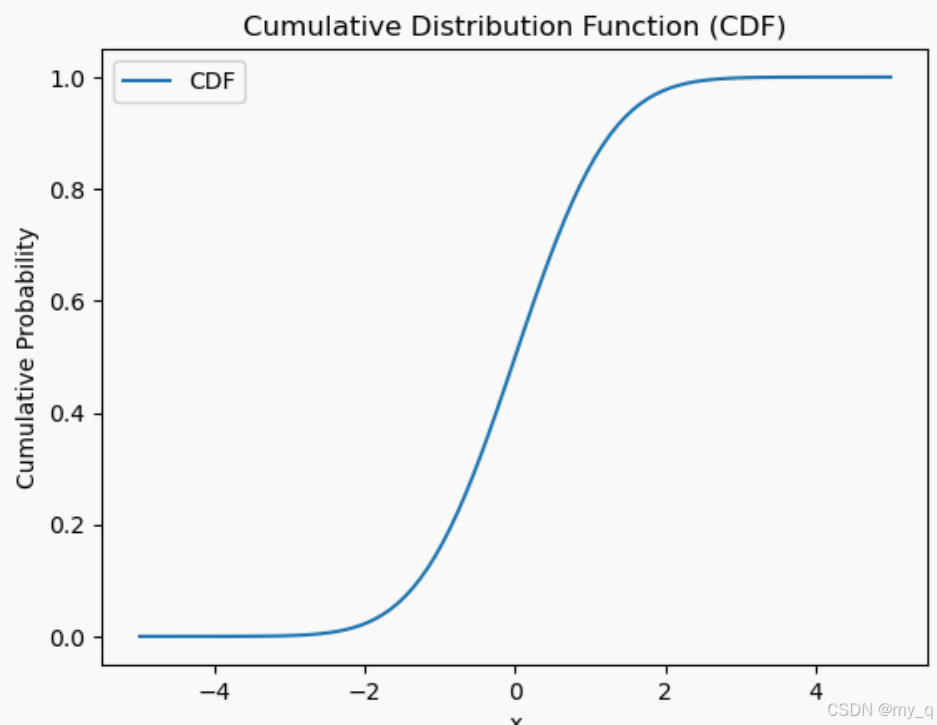
累积分布函数（CDF）：累积分布函数（CDF）给出了随机变量小于或等于某个特定值的概率。对于一个随机变量X，其累积分布函数可表示为F(x)。给定一个特定的x，F(x)表示随机变量X小于或等于x的概率

示例代码：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# 创建一个正态分布随机变量
mu = 0  # 均值
sigma = 1  # 标准差
rv = norm(loc=mu, scale=sigma)

# 绘制概率密度函数（PDF）
x = np.linspace(-5, 5, 100)  # x轴范围
pdf = rv.pdf(x)  # 计算概率密度函数的值
plt.plot(x, pdf, label='PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('Probability Density Function (PDF)')
plt.legend()

# 绘制累积分布函数（CDF）
cdf = rv.cdf(x)  # 计算累积分布函数的值
plt.figure()
plt.plot(x, cdf, label='CDF')
plt.xlabel('x')
plt.ylabel('Cumulative Probability')
plt.title('Cumulative Distribution Function (CDF)')
plt.legend()

# 显示图形
plt.show()

代码中使用了SciPy库中的 norm 函数来创建一个均值为0、标准差为1的正态分布随机变量。然后利用 pdf 方法计算概率密度函数的值，并使用 plot 函数绘制PDF曲线。接着，利用 cdf 方法计算累积分布函数的值，并使用 plot 函数绘制CDF曲线，执行上述代码后，将会显示出概率密度函数和累积分布函数的图像。这些图形可以帮助理解概率分布的特征，如密度的集中程度、分布的偏斜性以及随机变量小于或等于某个特定值的概率

4.均值、中位数与众数

均值（平均值）、中位数和众数是统计学中常用的描述数据集中趋势的指标，它们有不同的计算方法和应用场景

均值（平均值）是一组数据的总和除以数据的个数。均值可以反映数据集的平均水平。在计算均值时，每个数据点都被等同对待，无论其大小或重要性。均值对极端值较为敏感，因为它会受到所有数据点的影响
中位数是按照数值大小将一组数据划分为两个相等部分的值。中位数可被视为排序后的中间值，既不受极端值的影响，也不受数据分布的形态影响。中位数适用于处理存在异常值或偏斜分布的数据集
众数是一组数据中出现次数最多的值。众数对离散数据具有描述性，可以确定数据集中最常见的值或模式。一个数据集可以有一个或多个众数，甚至可能没有众数

在统计中的应用：

均值经常用作描述数据集整体趋势的指标，尤其适用于对称的数据分布。例如，在分析股票市场表现时，均值可以用来计算股票的平均收盘价
中位数常用于处理有离群值的数据集。例如，当研究收入分布时，中位数可以更好地反映普通人的收入水平，而不受富豪或贫困人群的影响
众数常用于描述离散型数据的最常见取值或模式。例如，研究一个班级学生的血型分布时，可能会找到最常见的血型并报告其为众数

一个例子

假设我们有一组考试成绩数据：65, 72, 81, 88, 90

均值：(65 + 72 + 81 + 88 + 90) / 5 = 79.2，均值表示这些成绩的平均水平
中位数：对数据进行排序后，中间值为81，中位数表示在一半学生的成绩高于81，另一半低于81
众数：没有重复的值，所以没有众数