这是上交团队发表在USENIX2024上的文章。
1 介绍
1.1 \(\text{MPC}\)和\(\text{PPML}\)
假设一个多方的场景,参与方分别持有数据\(x,y,z,w\),如果现在想要计算某个函数\(f(x,y,z,w)\),一种想法是引入可信方,让可信方帮忙进行计算。
而这样的问题实际上是多方安全计算(\(\text{MPC}\))想要研究的。\(\text{MPC}\)就是想要在不引入可信方的情况下,通过各方协作计算出\(f\)。
当\(f\)是一个机器学习模型时,我们称之为隐私保护机器学习(\(\text{PPML}\))。
1.2 安全模型分类
在\(\text{PPML}\)里,根据敌手的能力可以分为:
-
敌手只是对数据好奇,但不会对数据做任何修改,这称为半诚实的敌手;
-
敌手可能主动破坏数据,这称为恶意敌手。
在恶意敌手情况下,能继续进行细分。这里假设参与方总数为\(n\),破坏的参与方数量为\(t\):
-
当\(t<n/2\),称为诚实多数;
-
当\(t\ge n/2\),称为不诚实多数。
1.3 \(\text{PPML}\)协议的一般化构造
要提出一个\(\text{PPML}\)协议,一般需要包括两部分:第一部分是针对基本操作比如加法和乘法的底层\(\text{MPC}\)协议;第二部分是针对ML中特有的一些基本操作,比如向量点积、RELU需要的比较等。
有了以上两部分,就能去构造复杂的ML模型。
1.4 本文贡献
本文的主要贡献是:
-
为\(\text{PPML}\)设计了高效的协议:
-
带截断的乘法
-
向量点积
-
矩阵乘法
-
安全比较
-
-
首次在通用可组合(UC)框架下严格证明了所有协议的安全性。
-
对协议进行了实现和测试。
2 预备知识
2.1 \(\text{SPD}Z_{2^k}\)秘密分享机制
定义:
每个参与方持有一个MAC密钥的均匀随机加法份额\(\alpha^i\leftarrow Z_{2^s}\),将加法份额相加能得到一个全局的MAC密钥\(\alpha=\overset{n}{\sum}\limits_{i=1}\alpha^i \space \text{mod} \space 2^{k+s}\)。
假设元素\(x\in Z_{2^k}\)是被\([\cdot]{2^k}\)共享的,那么每个参与方\(P_i\)持有两个值\(x^i\in Z{2^{k+s}},m_{x}^i\in Z_{2^{k+s}}\)。其中\(x=\overset{n}{\sum}\limits_{i=1} x^i \space \text{mod}\space 2^k\)是被共享的元素,\(m_x=\overset{n}{\sum}\limits_{i=1}m_{x}^i\space \text{mod}\space 2^{k+s}\)是消息认证码。同时消息认证码满足:\(m_x=(\overset{n}{\sum}\limits_{i=1}x^i)\cdot \alpha \space \text{mod}\space 2^{k+s}\)。
最终记\([x]{2^k}=((x^1,\cdots,x^n),(m{x}^1,\cdots,m_{x}^n))\),即将元素\(x\)的分享表示成所有参与方持有的\(x\)份额和MAC份额组合在一起的形式。当\(2^k\)较大且上下文能明确时,将\([x]_{2^k}\)简记为\([x]\)。
秘密重构:
各参与方使用随机共享值\([r]\)对\(x\)的高\(s\)位进行掩码,得到\([\tilde x]=[x]+2^k[r]\)。用\(\tilde x^i,m_{\tilde x}^i\)表示参与方\(P_i\)的share和MAC share。
参与方会广播\(\tilde x^i\),进而进行计算:
\[\begin{aligned} \overset{n}{\sum}\limits_{i=1}\tilde x^i \space \text{mod}\space 2^k&=\tilde x\space \text{mod}\space 2^k \\ &=(x+2^kr)\space \text{mod}\space 2^k \\ &=x \space \text{mod}\space 2^k \\ &=x \end{aligned} \]
过程\(\pi_{\text{MACCheck}}\)会用来检查\(\text{MAC}\)。
加法:
\([x+y]=[x]+[y]\),加法是在本地计算的。
乘法:
分为两个阶段进行。
预处理截断:生成乘法三元组\(([a],[b],[c])\)。
在线阶段:
-
各参与方本地计算\([\delta_x]=[a]-[x],[\delta_y]=[b]-[y]\);
-
打开\(\delta_x,\delta_y\);
-
本地计算\([z]=[c]-\delta_x\cdot[b]-\delta_y\cdot[a]+\delta_x\cdot\delta_y\)。
2.2 依赖于电路的预处理技术(\(\text{CDP}\))
核心思想:
-
预处理阶段,参与方获得每条线路\(x\)对应的一个值\([\lambda_x]\);
-
在线阶段,对于每个电路门,参与方需要根据输入线路的\(\Delta\),计算并打开输出线路的\(\Delta\),其中\(\Delta x=x+\lambda_x\)。
\(\text{TurboSpeedz}\)协议:
\(\text{CDP}\)来源于\(\text{TurboSpeedz}\)协议,其使用的秘密分享与\(\text{SPD}Z_{2^k}\)类似,只不过数据都定义在有限域而不是环上,记作\(<\cdot>\)。
在预处理阶段,参与方需要准备一些依赖于电路的材料。
假设用\(x,y,z\)表示电路中的线路。假设对于电路中每一条线路\(z\),参与方都有一个共享值\(<\lambda_z>\):
-
如果\(z\)不是加法门的输出线路,那么\(\lambda_z\)是一个均匀随机值;
-
如果\(z\)是一个输入线路为\(x,y\)的加法门的输出线路,那么\(\lambda_z\)定义为\(\lambda_z=\lambda_x+\lambda_y\)。
对于每个乘法门,假设参与方拥有一个共享乘法三元组\((<a>,<b>,<c>)\)以及值\(\delta_x,\delta_y\),其中\(c=ab,\delta_x=a-\lambda_x,\delta_y=b-\lambda_y\)。
在在线阶段,各方根据预处理阶段准备的材料进行计算。
对线路\(x_1\)上的秘密值\(x\),参与方持有\(<x>\),且知道\(\Delta x=x+\lambda_x\)。
对于输入为\(x,y\)的加法门:参与方可以在本地计算\(<z>=<x>+<y>,\Delta z=\Delta x+\Delta y\)。
对于输入为\(x,y\)的乘法门:参与方的计算公式为\(<z>=(\Delta x+\delta_x)(\Delta y +\delta_y)-(\Delta y +\delta_y)<a>-(\Delta x+\delta_x)<b>+<c>\)。
正确性证明:
\[\Delta x+\delta_x=(x+\lambda_x)+(a-\lambda_x)=x+a,\Delta_y+\delta_y=y+b \]
那么等式右边为:\((x+a)(y+b)-(y+b)a-(x+a)b+ab=xy=z\)。
本文为了使计算在环\(Z_{2^k}\)上进行,将\(\text{CDP}\)过程底层的秘密分享机制从\(<>\)改为\([]\),这两种分享其实就是把数据范围改换了一下。
在本文具体使用的\(\text{CDP}\)协议中,会依赖\(F_{Prep}\)函数。该函数有3个命令:
-
Triple:生成一个乘法三元组
-
Rand:为所有参与方生成一个随机共享的元素
-
Input:生成一个随机共享的元素\([r]\),且某一方确切知道r
本文使用的算术电路预处理协议\(\Pi_{\text{PrepArith}}\):
各参与方按照电路拓扑顺序进行操作,这样能保证电路输入已经在前面的门得到。
输入:对于参与方\(P_i\)的每条输入线路\(x\),通过调用\(F_{Prep}\)的Input命令,\(P_i\)能知道\(\lambda_x\),所有参与方获得对应的共享值\([\lambda_x]\)。
加法:对于输入线路为\(x,y\)且输出线路为\(z\)的加法门,所有参与方在本地计算\([\lambda_z]=[\lambda_x]+[\lambda_y]\)。
乘法:对于输入线路为\(x,y\)且输出线路为\(z\)的乘法门,参与方执行以下操作:
-
调用\(F_{Prep}\)的Triple命令,获取乘法三元组\(([a],[b],[c])\);
-
在本地计算\([\delta_x]=[a]-[\lambda_x],[\delta_y]=[b]-[\lambda_y]\);
-
调用\(F_{Prep}\)的Rand命令,获取\([\lambda_z],\lambda_z\leftarrow Z_{2^k}\);
此时,对于一个乘法门,各参与方拥有\([a],[b],[c],[\lambda_z],[\delta_x],[\delta_y]\)。
输出:各参与方公开每个乘法门的共享\([\delta]\),让所有参与方都能知道这些值。并运行\(\pi_{MACCheck}\)检查已经公开值的MAC。
\(\Pi_{\text{PrepArith}}\)的目的:
-
为每条线路生成共享的\([\lambda]\);
-
为每个乘法门生成一个共享的乘法三元组;
-
为每个乘法门生成两个公开的\(\delta\)(\(\delta_x,\delta_y\));
本文使用的算术电路在线协议\(\Pi_{\text{OnlineArith}}\):
初始化:参与方使用电路调用\(F_{PrepArith}\),以获取\(\delta\)值、共享的\([\lambda]\)值以及每个门电路的乘法三元组。然后,参与方按照拓扑顺序进行操作。
输入:为了让参与方共享输入值\(x\),\(P_i\)计算并广播\(\Delta x=x+\lambda_x\),那么所有参与方获得\(\Delta x\);
加法:对于输入线路为\(x,y\)且输出线路为\(z\)的加法门,参与方在本地计算\(\Delta z=\Delta x+\Delta y\)。
乘法:对于输入线路为\(x,y\)且输出线路为\(z\)的乘法门,所有参与方执行以下操作:
-
在本地计算\([\Delta z]=(\Delta x+\delta_x)(\Delta y+\delta_y)-(\Delta y+\delta_y)[a]-(\Delta x+\delta_x)[b]+[c]+[\lambda_z]\);
-
公开\([\Delta z]\),得到\(\Delta z\);
输出:为了输出线路\(x\)上的值,所有参与方执行以下操作:
- 在本地计算\([x]=\Delta x-[\lambda_x]\)并公开。
\(\Pi_{\text{OnlineArith}}\)的目的:
-
获取每条线路的\(\Delta\);
-
得到输入\(x\)的秘密分片;
3 \(\text{PPML}\)协议
核心思想是利用\(\text{CDP}\)来改进后续的协议。
3.1 带截断的乘法
首先来看传统的截断,其目的是将乘法未截断的值\([z']\)截断为\([z]\)。其中\(z=z'/2^d\)。
使用的方法如下:
预处理阶段:生成一对共享的随机值\(([r^{'}],[r])\),其中\(r=r^{'}/2^d\)。
在线阶段:
-
参与方计算\([c^{'}]=[z^{'}]+[r^{'}]\);
-
计算\(c=c^{'}/2^d\);
-
本地计算\([z]=c-[r]\)。
观察\(\Pi_{\text{OnlineArith}}\),发现已经公开了\(\Delta z^{'}=z^{'}+\lambda_z^{'}\)。假设参与方拥有\([\lambda_z]\),那么可以计算:
\[z=\Delta z-\lambda_z=\Delta z^{'}/2^d-\lambda_z^{'}/2^d=z^{'}/2^d \]
即将\([\lambda_z^{'}],[\lambda_z]\)不仅充当掩码,还充当截断对。
本文使用\(F_{edaBits}\)来获得该截断对。
具体的带截断乘法过程\(\pi_{\text{MultTrunc}}\):
输入线路为\(x,y\),输出线路为\(z\),目标是计算\(x,y\)的乘积并进行截断。
预处理阶段:
-
参与方执行\(F_{Prep}\)的Triple命令获得\(([a],[b],[c])\);
-
参与方计算\([\delta_x]=[a]-[\lambda_x],[\delta_y]=[b]-[\lambda_y]\)并公开\(\delta_x,\delta_y\);
-
参与方对输入\((k-d)\)执行\(F_{edaBits}\),获得\([\lambda_z]\)及其位分解\(\lbrace [\lambda_{z,i}]2\rbrace{i=0}^{k-d-1}\);
-
参与方对输入\(d\)执行\(F_{edaBits}\),获得\([u]\)及其位分解\(\lbrace [u_i]2\rbrace{i=0}^{d-1}\);
-
参与方在本地计算\([\lambda_{z^{'}}]=2^d\cdot [\lambda_z]+[u]\);
在线阶段:
-
参与方在本地计算\([\Delta z^{'}]=(\Delta x+\delta_x)(\Delta y+\delta_y)-(\Delta y+\delta y)[a]-(\Delta x+\delta x)[b]+[c]+[\lambda_{z^{'}}]\);
-
参与方公开\([\Delta z^{'}]\)得到\(\Delta z^{'}\);
-
参与方在本地计算\(\Delta z=\Delta z^{'}/2^d\);
之前方法需要先进行乘法,再进行截断。新方法在乘法过程中,将两个过程进行结合,计算得到\(\Delta z^{'}\)并打开后,直接本地截断。
由于乘法通信量是2elements/party,截断通信量为1elements/patry,那么原方法通信量就是3elements/party,且需要2轮交互。而本文方法通信量为1element/party,且仅需一轮交互。
3.2 向量点积
为了方便,规定可以对向量使用\([\cdot]\)表示法,\([\vec \lambda]\)表示向量\(\lambda\)的每个元素都是通过\([\cdot]\)进行秘密共享的。
向量乘法的目的是输入长度为\(m\)的向量\(\vec x,\vec y\),输出线路\(z\)的值,其中\(z=\vec x\cdot \vec y\)。一种简单方法是针对每一个底层乘法执行\(\Pi_{OnlineArith}\),但这样会导致在线通信量与向量长度呈线性关系。
向量点积过程\(\pi_{\text{DotProduct}}\):
对于一个输入线路为长度为\(m\)的向量\(x,y\)的点积门:
预处理阶段:
-
参与方执行\(F_{Prep}\)的Rand方法,获得\([\lambda_z],\lambda_z\leftarrow Z_{2^k}\),随机份额将用于在线阶段对最终结果进行掩码;
-
参与方执行\(F_{Prep}\)的Triple方法\(m\)次获得\(m\)个三元组,得到\([\vec a],[\vec b],[\vec c]\),其中第\(i\)次得到的三元组是\(([\vec a[i]]),[\vec b[i]],[\vec c[i]]\);
-
参与方计算\([\vec {\delta_x}]=[\vec a]-[\vec{\lambda_x}],[\vec {\delta_y}]=[\vec b]-[\vec {\lambda_y}]\)并公开;
在线阶段:
-
参与方在本地计算\([\Delta z]=\overset{m}{\sum}\limits_{i=1}((\vec {\Delta x}[i]+\vec {\delta_x}[i])(\vec {\Delta y}[i]+\vec {\delta_y}[i])-(\vec {\Delta y}[i]+\vec {\delta_y}[i])[\vec a[i]]-(\vec {\Delta x}[i]+\vec {\delta_x}[i])[\vec b[i]]+[\vec c[i]])+[\lambda_z]\);
-
参与方公开\([\Delta z]\)获得\(\Delta z\);
简单方法中,每对\(x_i,y_i\)做乘法的通信量是2elements/party,那么长度为\(m\)的向量乘法需要的通信量就是2m/elements/party。而本文方法通信量为1element/party。
在向量点积优化的基础上,就可以去优化其他操作,比如矩阵乘法、带截断的向量点积、带截断的矩阵乘法等。
3.3 安全比较
首先介绍掩码比较技术,目的是比较\(x\)与0的大小:
预处理阶段:
- 参与方执行\(F_{\text{edaBits}}\)得到共享随机掩码\([r]\)及其位分解\(\lbrace [r_i]2\rbrace{i=0}^{k-1}\);
在线阶段:
-
参与方计算\([c]=[x]+[r]\)并公开\([c]\);
-
参与方使用逐位比较电路来比较\(c\)和\(\lbrace [r_i]2\rbrace{i=0}^{k-1}\),获得\([z]_2,z=(c<r)=(x+r<r)=(x<0)\);
-
使用\(B2A\)协议将\([z]_2\)转为\([z]\);
安全比较具体过程\(\pi_{\text{LTZ}}\):
参与方输入为\([\lambda_x],\Delta x(\Delta x=\lambda_x+x)\),希望得到\([\lambda_z],\Delta z\)。
\(\text{LTZ}\)门的输入为线路\(x\),目的是在线路\(z\)得到比较结果\(z=(x<0)\)。
预处理阶段:
-
参与方在输入\(k\)上执行\(F_{edaBits}\)获得\([r]\)及其位分解;
-
参与方计算\([\delta_x]=[r]-[\lambda_x]\),并公开\(\delta_x\);
-
参与方执行\(F_{Prep}\)的Rand方法获得\([\lambda_z],\lambda_z\leftarrow Z_{2^k}\);
在线阶段:
-
参与方执行\(\pi_{BitLT}(\Delta x+\delta_x,\lbrace [r_i]2\rbrace{i=0}^{k-1})\)来获得\([z]_2\);
-
参与方执行\(B2A\)将\([z]_2\)转为\([z]\);
-
参与方在本地计算\([\Delta z]=[\lambda_z]+[z]\);
-
参与方打开\(\Delta z\)。
4 实验
实验聚焦两方计算场景,将MD-ML与\(\text{SPD}Z_{2^k}\)进行比较。
在线阶段,搭建AlexNet模型在CIFAR-10, Tiny ImageNet, ImageNet上做推理,结果如下:
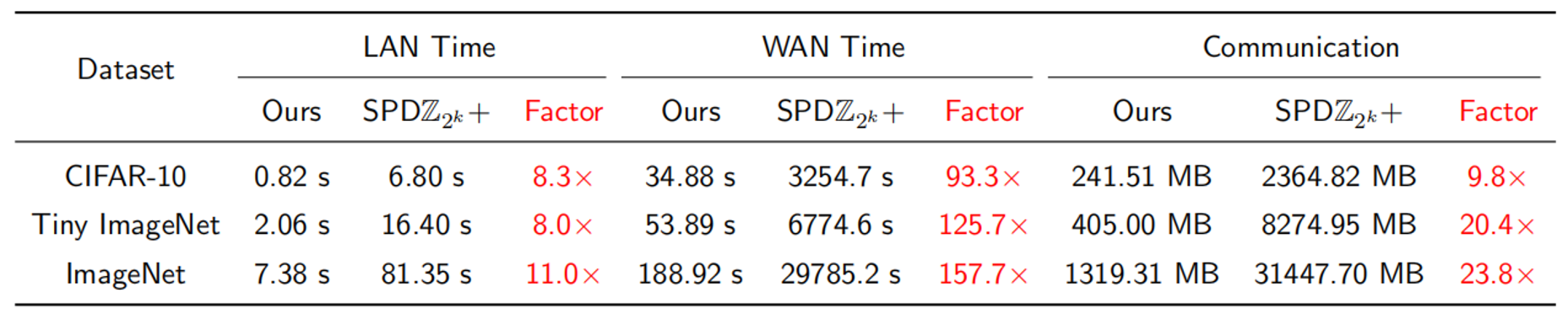
搭建ResNet-18模型在CIFAR-10上做推理,由于\(\text{SPD}Z_{2^k}\)没有做这组实验,仅呈现了MD-ML的效果:
