ZKW 非递归线段树详解

在算法竞赛和高性能计算场景中，线段树（Segment Tree） 是一个必修的数据结构。它可以在 O(\\log n) 时间内高效地完成区间查询与修改，比如：区间求和/最大/最小值查询配合区间加法/乘法/赋值操作。

经典线段树都是递归实现，即"从顶到底地去访问"整棵树。这种方式功能强大、可拓展性高，不过代码量稍大，实现起来相对"啰嗦"。运行时的函数递归开销大，尤其在多次深度递归调用时。

那么，是否有一种实现方式，可以去掉递归、保留高性能、更紧凑简洁？这时候，我们要介绍主角------zkw线段树。

🧠 什么是 zkw 线段树？

zkw 线段树的名称来源于一位中国信息学竞赛（由他发明）。这是一个 非递归实现的线段树结构。它的设计核心是：通过自底向上的迭代方式完成查询和修改操作。

相比传统递归线段树，zkw 在以下几个方面有明显优势：

• 完全去除递归，避免函数栈开销，这也使得常数极小，运行速度优于递归版约 10%~30%
• 逻辑紧凑，代码量少，对手写友好，非常适合比赛中快速实现；

当然，它也并非万能，当你需要支持更复杂的操作如区间乘法、赋值、合并区间信息时，他的结构不易再支撑复杂操作，改用传统递归线段树反而更灵活、更强大。

📚 zkw 线段树的结构变化

zkw 线段树底层是如何组织数据的？其仍然用数组模拟一个二叉树。

zkw 线段树的核心思想仍是使用数组模拟一棵二叉树 ，将所有叶子节点排列在数组的下半部分，内节点放在上半部分，自底向上维护区间信息。按照提出者传下的惯例，通常将大小向上对齐到二的次幂（\(N\) 是原数组大小，找一个大于等于 \(N\) 的最小的 2\^k，记为 \(base\)（通常为\(2^{\lceil \log_2 N \rceil}\)），保证线段树是一个完美二叉树。

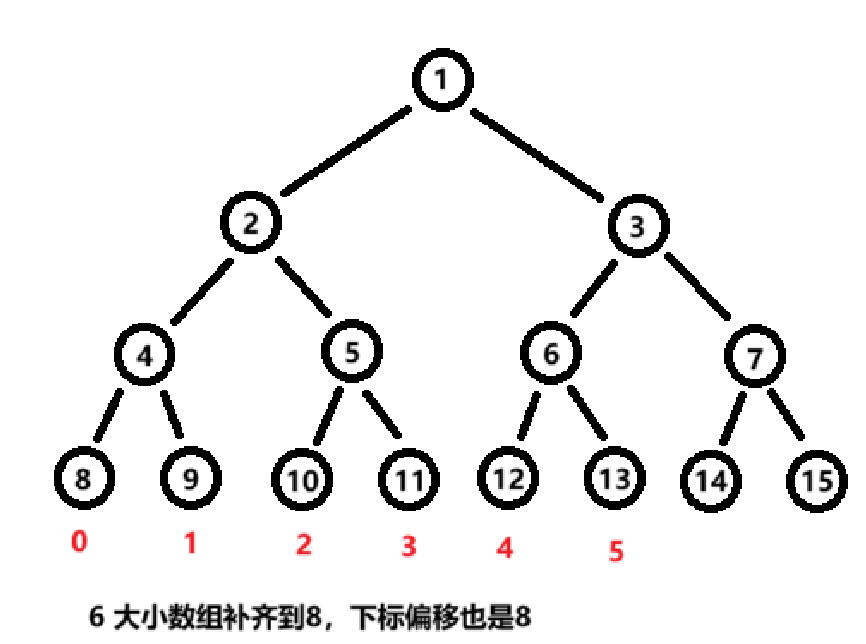
整个线段树数组大小为 \(2 * base\)，惯例从 1 为根节点开始编号（有些实现从 0）；

位置	编号范围	说明
根节点	1	整个区间 [0, N-1]
内部节点	\([1, base - 1]\)	管理子区间信息
叶子节点	\([base, base + N - 1]\)	原数组元素对应位置

自底向上维护区间信息

zkw 的精妙之处在于：所有查询与更新操作都从叶子节点开始，向上合并区间信息。传统线段树从根节点出发，将一个区间拆分为对数个区间；而我们从目标区间的两个端点处的叶节点出发，也可以找到要拆分的区间。

为了进行区间拆分，我们想象两个指针在两个叶节点端点处，每一轮，如果左端点是一个左儿子，那么上跳（因为其父节点仍在区间内）；但如果左端点是一个右儿子，则其应该被单独拆分出来，讨论掉他后，左端点向右移（然后再上跳）。右端点同理。直到他们相遇，所有拆分的节点就是拆分出的子区间。

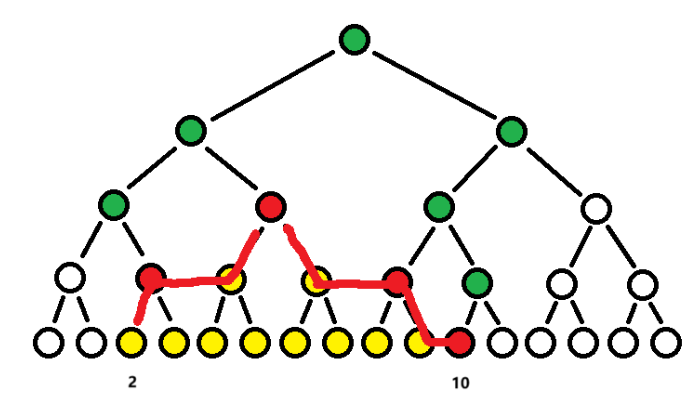
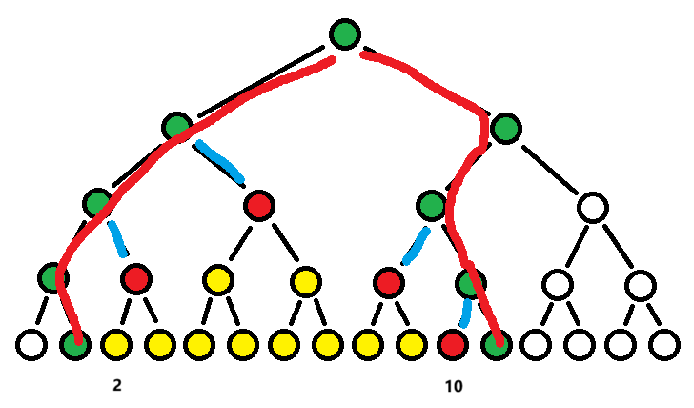
如图所示，假定要更新区间。访问 \([2, 10]\) 将最终被拆分为 4 个区间（红色节点），黄色为在范围内但由懒标记保护不用更新的大规模下层节点（被红色完全覆盖），而绿色则为会被红色节点影响，需要被 pushUp 的上层节点（同时也是经典线段树中根节点访问 \([2, 10]\) 的路径）。

🔄 zkw 线段树的实现

建树

计算出稍大于原数组的二次幂大小，构建二叉树。取原数组直接平移到叶节点处即可，然后生成非叶节点的和。

区间修改

对于拆分出的每个区间，都进行修改并更新懒标记（红点）。同时，绿点的总和值也会受到影响，所以他们需要被 pushUp（即两个叶节点到根节点路径上的所有点）

注意，pushUp 需要更新自身的值为子节点值之和+自身的懒标记。因为懒标记不总会被我们主动下推。

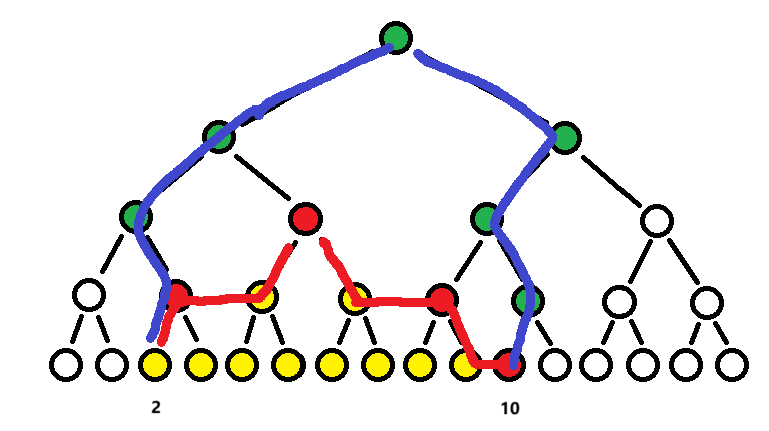
区间和

对于拆分出的每个区间，都直接统计其值（红点）。同时，绿点存在的懒标记也可能影响到总和，所以在正式求和之前，将他们全部下推到底（从两个叶节点到顶点路上的所有点，从上往下推下来）。

// 0-based 闭区间
class zkwSegmentTree {
    int n;                      // 实际元素个数
    int M;                      // 叶子起点（2 的幂）
    vector<long long> sum;
    vector<long long> lazy;
    vector<int> len;            // 每个结点管辖区间长度（不必须，也可以计算）

    inline void apply(int x, long long val) {
        sum[x]  += val * len[x];
        lazy[x] += val;
    }

    inline void pushUp(int x) {
        sum[x] = sum[x << 1] + sum[x << 1 | 1] + lazy[x] * 1LL * len[x];
    }

    inline void pushDown(int x) {
        if (lazy[x] == 0) return;
        apply(x << 1,     lazy[x]);
        apply(x << 1 | 1, lazy[x]);
        lazy[x] = 0;
    }

    // 把从根到 x 的路径上所有懒标记一层层下推
    inline void pushDownPath(int x) {
        static int stk[25];      // log2(2e5) ≈ 18，足够
        int top = 0;
        for (x >>= 1; x; x >>= 1) stk[top++] = x;
        while (top) pushDown(stk[--top]);
    }

public:
    explicit zkwSegmentTree(const vector<long long>& a) {
        n = (int)a.size();
        M = 1; while (M < n) M <<= 1;          // 2 的幂
        sum.assign(M << 1, 0);
        lazy.assign(M << 1, 0);
        len .assign(M << 1, 0);

        // 预计算区间长度
        for (int i = M; i < (M << 1); ++i) len[i] = 1;
        for (int i = M - 1; i; --i) len[i] = len[i << 1] + len[i << 1 | 1];

        // 叶子赋初值
        for (int i = 0; i < n; ++i) sum[M + i] = a[i];
        // 自底向上求和
        for (int i = M - 1; i; --i) sum[i] = sum[i << 1] + sum[i << 1 | 1];
    }

    void add(int l, int r, long long val) { 
        int L = l + M, R = r + M;

        int l0 = L, r0 = R;            // 记录，待会儿 pushUp
        while (L <= R) {
            if (L & 1) apply(L++, val);    // 若 L 是右儿子，则整段属于答案
            if (!(R & 1)) apply(R--, val); // 若 R 是左儿子
            L >>= 1;  R >>= 1;
        }
        // 分别沿两条端点路径向上刷新，注意从最近祖先到根节点也需要更新
        for (int i = l0 >> 1; i; i >>= 1) pushUp(i);
        for (int i = r0 >> 1; i; i >>= 1) pushUp(i);
    }

    long long query(int l, int r) {
        int L = l + M, R = r + M;
        pushDownPath(L);
        pushDownPath(R);

        long long ans = 0;
        while (L <= R) {
            if (L & 1) ans += sum[L++];    // L 为右儿子，整段可取
            if (!(R & 1)) ans += sum[R--]; // R 为左儿子
            L >>= 1;  R >>= 1;
        }
        return ans;
    }
};

标记永久化方法

对于这道题来说（求和），除此在求和前下推所有需要的标记以外，还有一个思路：根本不下传标记，而是让标记永久停留在它被打下去的结点上，在真正需要它的那一刻------查询时------再即时计算它对答案的贡献。这个思路被称为标记永久化（Tag Persistence）。

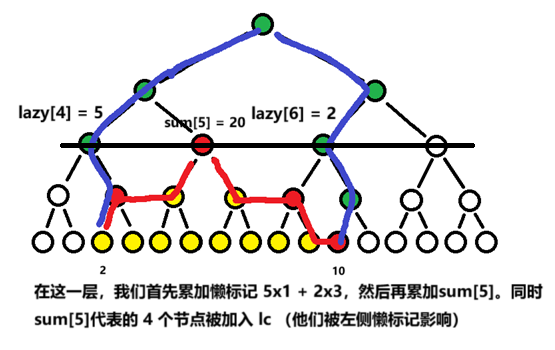
具体来说在查询时，我们不使用 pushDownPath，而是现场计算每个绿点的懒标记对答案的贡献并累加。懒标记绝不往下传递，也不更新子结点。

对于上面代码，我们可以选择这样的写法：维护两组指针，一组正常向上分解区间，另外一组总是从边缘叶节点往上跳（保证他们覆盖所有的绿色节点），每次计算时，计算绿色节点持有的懒标记带来的贡献（懒标记值乘以左侧（或右侧）已计算的数的个数）。

long long range_query(int l, int r) {
    int L = l + M, R = r + M;
    // pushDownPath(L);
    // pushDownPath(R);
    int tl = L, tr = R, lc = 0, rc = 0;

    long long ans = 0;
    while (L <= R) {
        ans += lazy[tl] * lc + lazy[tr] * rc; // 计算本层的绿色节点懒标记
        if (L & 1) ans += sum[L++], lc += len[L - 1];
        if (!(R & 1)) ans += sum[R--], rc += len[R + 1];
        L >>= 1;  R >>= 1; tl >>= 1; tr >>= 1;
    }
    while (tl) { // 懒标记计算还要持续到根节点
        ans += lazy[tl] * lc + lazy[tr] * rc;
        tl >>= 1; tr >>= 1;
    }
    return ans;
}

按照这个思路，经典线段树实际上也可以在某些情况不推标记，只是不能带来任何好处。

开区间拆分法

其实原作者提出的区间拆分并非如此，原作者提出的思路是，将目标区间 \([L,R]\) 视作开区间 \((L-1,R+1)\)，并在外侧的两个点开始向上。每一轮，如果左端点是一个左儿子，其右儿子被单独拆分，讨论掉他后上跳。右端点同理。直到他们互为兄弟，此时结束上跳。最后处理他们和他们的父节点（以及从父节点开始连接到根节点的更新）。

这种方法也很直观，不过需要额外处理目标区间由 0 开头或者在最后结束的情况（添加哨兵）

这种写法的代码略。

⚖️ 优点和劣势

特性	zkw 线段树	经典线段树	树状数组 (Fenwick)
更新复杂度	O(log n)	O(log n) (较大常数)	O(log n)
查询复杂度	O(log n)	O(log n) (较大常数)	O(log n)
常数开销	低（无下推一般较优，也无递归调用）	较高（函数递归＋下推）	极低（迭代加减）
代码简洁度	高	中	高（接口单一）
支持操作	区间加法、区间乘法等可叠加标记	任意可合并区间操作	仅点更新＋前缀和查询
复杂懒标记维护	★★☆☆☆	★★★★☆	---
扩展性	较差（赋值、多种标记叠加难）	最强（各种懒标记、区间合并）	差（只能单一标记）

zkw 利用端点自底向上累加祖先的懒标记，去掉了所有下推逻辑和递归调用，因而常数极小、代码量少。但它只能高效支持「可叠加」的懒标记，遇到区间赋值、区间最小/最大查询等更复杂的懒标记场景时，维护逻辑很快就会变得繁琐且易错。
经典递归线段树 功能最全，支持任意组合的懒标记和区间合并，扩展性强；唯一代价是模板较长、运行时有函数调用和下推开销。
树状数组 则针对点更新＋前缀/区间和查询做了极致优化，代码最简；但它天生不适合「赋值覆盖」「区间乘法」等复杂操作。

随着维护的问题越来越复杂，各类懒标记（赋值、乘法、异或、区间合并等）层出不穷，标记永久化方案的管理成本会迅速飙升，原本"少写几个函数""去掉下推"的优势也将逐渐丧失。 所以其不能完全取代经典线段树。