坐标系和相机标定介绍，张正友标定法原理，opencv标定

tony3652025-07-17 9:55

文章目录

  • 坐标系介绍
      • [**1. 世界坐标系（World Coordinate System, WCS）**](#1. 世界坐标系（World Coordinate System, WCS）)
      • [**2. 相机坐标系（Camera Coordinate System, CCS）**](#2. 相机坐标系（Camera Coordinate System, CCS）)
      • [**3. 图像坐标系（Image Coordinate System, ICS）**](#3. 图像坐标系（Image Coordinate System, ICS）)
      • [**4. 像素坐标系（Pixel Coordinate System, PCS）**](#4. 像素坐标系（Pixel Coordinate System, PCS）)
      • [**5. 四者转换的全过程**](#5. 四者转换的全过程)
      • [**6. 关键区别总结**](#6. 关键区别总结)
      • [**7. 实例说明**](#7. 实例说明)
      • [**8. 应用意义**](#8. 应用意义)
  • 张正友标定方法
    • **概述**
    • [**1. 标定流程概述**](#1. 标定流程概述)
    • [**2. 核心数学原理**](#2. 核心数学原理)
      • [**2.1 相机模型**](#2.1 相机模型)
      • [**2.2 单应性矩阵（Homography）**](#2.2 单应性矩阵（Homography）)
      • [**2.3 约束条件求内参 K K K**](#2.3 约束条件求内参 K K K)
        • [**2.3.1 单应性矩阵 H H H 的定义**](#2.3.1 单应性矩阵 H H H 的定义)
        • [**2.3.2 利用旋转矩阵的正交性约束**](#2.3.2 利用旋转矩阵的正交性约束)
        • [**2.3.3 定义 B = K − T K − 1 B = K^{-T} K^{-1} B=K−TK−1**](#2.3.3 定义 B = K − T K − 1 B = K^{-T} K^{-1} B=K−TK−1)
        • [**2.3.4 构建线性方程组**](#2.3.4 构建线性方程组)
        • [**2.3.5 求解 b b b（最小二乘解）**](#2.3.5 求解 b b b（最小二乘解）)
        • [**2.3.6 从 B B B 分解出 K K K**](#2.3.6 从 B B B 分解出 K K K)
        • [**2.3.7 示例计算**](#2.3.7 示例计算)
        • [**2.3.8 总结步骤**](#2.3.8 总结步骤)
      • [**2.4 求解外参 R , t R, t R,t**](#2.4 求解外参 R , t R, t R,t)
      • [**2.5 畸变校正**](#2.5 畸变校正)
    • [**3. 优化（Bundle Adjustment）**](#3. 优化（Bundle Adjustment）)
    • [**4. 算法总结**](#4. 算法总结)
    • [**5. 实际应用（OpenCV示例）**](#5. 实际应用（OpenCV示例）)
      • [**5.1 准备标定板**](#5.1 准备标定板)
      • [**5.2 采集多角度标定图像**](#5.2 采集多角度标定图像)
      • [**5.3 检测角点并建立2D-3D对应关系**](#5.3 检测角点并建立2D-3D对应关系)
      • [**5.4 标定相机并获取畸变系数**](#5.4 标定相机并获取畸变系数)
      • [**5.5 验证标定结果**](#5.5 验证标定结果)
      • [**5.6 畸变系数详解**](#5.6 畸变系数详解)
      • [**5.7 注意事项**](#5.7 注意事项)
      • [**5.8 完整代码示例**](#5.8 完整代码示例)
    • [**6. 总结**](#6. 总结)

坐标系介绍

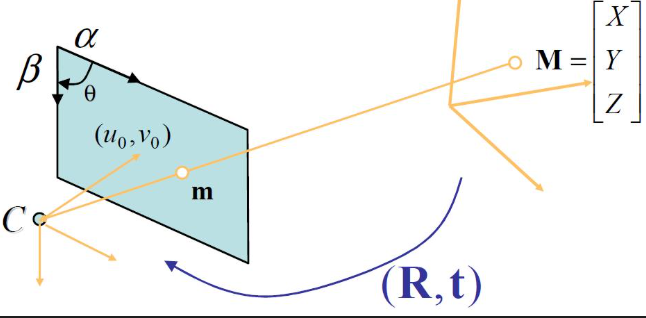
在计算机视觉和摄影测量中，世界坐标系、相机坐标系、图像坐标系和像素坐标系是描述三维空间到二维图像映射过程的四个关键坐标系。以下是它们的详细解释和相互关系：

1. 世界坐标系（World Coordinate System, WCS）

  • 定义：描述物体在真实三维空间中的绝对位置，是用户自定义的全局参考系。
  • 表示 ：
    • 点坐标： ( X w , Y w , Z w ) (X_w, Y_w, Z_w) (Xw,Yw,Zw)
    • 通常以标定板的某个角为原点，标定板平面为 Z w = 0 Z_w = 0 Zw=0。
  • 作用 ：
    提供物体在现实世界中的位置基准，用于多相机系统或场景重建。

2. 相机坐标系（Camera Coordinate System, CCS）

  • 定义：以相机光心为原点的三维坐标系，描述物体相对于相机的位置。
  • 表示 ：
    • 点坐标： ( X c , Y c , Z c ) (X_c, Y_c, Z_c) (Xc,Yc,Zc)
    • 光轴方向为 Z c Z_c Zc 轴， X c X_c Xc、 Y c Y_c Yc 轴分别与图像的横纵轴平行。
  • 与世界坐标系的关系 ：
    通过刚体变换 （旋转矩阵 R R R 和平移向量 t t t）关联：

    X c Y c Z c 1 \] = \[ R t 0 1 \] \[ X w Y w Z w 1 \] \\begin{bmatrix} X_c \\\\ Y_c \\\\ Z_c \\\\ 1 \\end{bmatrix} = \\begin{bmatrix} R \& t \\\\ 0 \& 1 \\end{bmatrix} \\begin{bmatrix} X_w \\\\ Y_w \\\\ Z_w \\\\ 1 \\end{bmatrix} XcYcZc1 =\[R0t1\] XwYwZw1

    将世界坐标转换为相机视角下的坐标，是三维到二维投影的中间步骤。

3. 图像坐标系（Image Coordinate System, ICS）

  • 定义：相机成像平面上的二维坐标系，单位为物理尺寸（如毫米）。
  • 表示 ：
    • 点坐标： ( x , y ) (x, y) (x,y)
    • 原点 O O O 为光轴与成像平面的交点（主点）。
  • 与相机坐标系的关系 ：
    通过透视投影 （针孔模型）转换：
    x = f ⋅ X c Z c , y = f ⋅ Y c Z c x = \frac{f \cdot X_c}{Z_c}, \quad y = \frac{f \cdot Y_c}{Z_c} x=Zcf⋅Xc,y=Zcf⋅Yc
    其中 f f f 为焦距。
  • 作用 ：
    描述物体在成像平面上的物理位置，尚未离散化为像素。

4. 像素坐标系（Pixel Coordinate System, PCS）

  • 定义：数字图像中的离散像素坐标系，原点通常在图像左上角。
  • 表示 ：
    • 点坐标： ( u , v ) (u, v) (u,v)
    • 单位为像素， u u u 为列号（向右增长）， v v v 为行号（向下增长）。
  • 与图像坐标系的关系 ：
    通过内参矩阵 K K K 转换：

    u v 1 \] = \[ 1 d x 0 c x 0 1 d y c y 0 0 1 \] \[ x y 1 \] \\begin{bmatrix} u \\\\ v \\\\ 1 \\end{bmatrix} = \\begin{bmatrix} \\frac{1}{dx} \& 0 \& c_x \\\\ 0 \& \\frac{1}{dy} \& c_y \\\\ 0 \& 0 \& 1 \\end{bmatrix} \\begin{bmatrix} x \\\\ y \\\\ 1 \\end{bmatrix} uv1 = dx1000dy10cxcy1 xy1 其中： * d x , d y dx, dy dx,dy：单个像素的物理尺寸（如毫米/像素） * ( c x , c y ) (c_x, c_y) (cx,cy)：主点在像素坐标系中的坐标。

    u = x d x + c x , v = y d y + c y u = \frac{x}{dx} + c_x, \quad v = \frac{y}{dy} + c_y u=dxx+cx,v=dyy+cy
  • 作用 ：
    最终映射到数字图像的像素位置，用于图像处理算法。

5. 四者转换的全过程

从世界坐标到像素坐标的完整流程：

  1. 世界坐标 → 相机坐标 （刚体变换）：

    X c Y c Z c \] = R \[ X w Y w Z w \] + t \\begin{bmatrix} X_c \\\\ Y_c \\\\ Z_c \\end{bmatrix} = R \\begin{bmatrix} X_w \\\\ Y_w \\\\ Z_w \\end{bmatrix} + t XcYcZc =R XwYwZw +t

    x = f ⋅ X c Z c , y = f ⋅ Y c Z c x = f \cdot \frac{X_c}{Z_c}, \quad y = f \cdot \frac{Y_c}{Z_c} x=f⋅ZcXc,y=f⋅ZcYc
  2. 图像坐标 → 像素坐标 （离散化 + 内参）：
    u = f d x ⋅ X c Z c + c x , v = f d y ⋅ Y c Z c + c y u = \frac{f}{dx} \cdot \frac{X_c}{Z_c} + c_x, \quad v = \frac{f}{dy} \cdot \frac{Y_c}{Z_c} + c_y u=dxf⋅ZcXc+cx,v=dyf⋅ZcYc+cy
    合并为矩阵形式：

    u v 1 \] = K \[ X c / Z c Y c / Z c 1 \] , K = \[ f x 0 c x 0 f y c y 0 0 1 \] \\begin{bmatrix} u \\\\ v \\\\ 1 \\end{bmatrix} = K \\begin{bmatrix} X_c/Z_c \\\\ Y_c/Z_c \\\\ 1 \\end{bmatrix}, \\quad K = \\begin{bmatrix} f_x \& 0 \& c_x \\\\ 0 \& f_y \& c_y \\\\ 0 \& 0 \& 1 \\end{bmatrix} uv1 =K Xc/ZcYc/Zc1 ,K= fx000fy0cxcy1 其中 f x = f / d x f_x = f/dx fx=f/dx， f y = f / d y f_y = f/dy fy=f/dy。

6. 关键区别总结

坐标系 维度 原点 单位 作用
世界坐标系 3D 场景自定义点 毫米/米 全局参考基准
相机坐标系 3D 相机光心 毫米 描述物体相对相机的位置
图像坐标系 2D 光轴与成像平面交点 毫米 物理成像平面位置
像素坐标系 2D 图像左上角 像素 数字图像处理的实际坐标

7. 实例说明

假设一个物体在世界坐标系中的位置为 ( 100 , 50 , 200 ) (100, 50, 200) (100,50,200) mm：

  1. 相机坐标 ：通过外参 R , t R, t R,t 计算 ( X c , Y c , Z c ) (X_c, Y_c, Z_c) (Xc,Yc,Zc)
  2. 图像坐标 ：投影到 ( x , y ) = ( f ⋅ X c / Z c , f ⋅ Y c / Z c ) (x, y) = (f \cdot X_c/Z_c, f \cdot Y_c/Z_c) (x,y)=(f⋅Xc/Zc,f⋅Yc/Zc)
  3. 像素坐标 ：转换为 ( u , v ) = ( x / d x + c x , y / d y + c y ) (u, v) = (x/dx + c_x, y/dy + c_y) (u,v)=(x/dx+cx,y/dy+cy)

若 f x = 500 f_x = 500 fx=500, c x = 320 c_x = 320 cx=320, c y = 240 c_y = 240 cy=240，则：
u = 500 ⋅ X c Z c + 320 , v = 500 ⋅ Y c Z c + 240 u = 500 \cdot \frac{X_c}{Z_c} + 320, \quad v = 500 \cdot \frac{Y_c}{Z_c} + 240 u=500⋅ZcXc+320,v=500⋅ZcYc+240

8. 应用意义

  • 相机标定 ：确定内参 K K K 和外参 R , t R, t R,t
  • 三维重建：从像素坐标反推世界坐标（需深度信息）
  • AR/VR：虚拟物体与真实世界的坐标对齐
  • 机器人导航：物体定位与路径规划

理解这些坐标系的转换关系，是计算机视觉中相机建模、标定和三维视觉任务的基础。

张正友标定方法

概述

张正友标定法（Zhang's Camera Calibration Method，2000年提出）是一种基于平面标定板的相机标定方法，广泛应用于计算机视觉和摄影测量领域。其核心思想是利用多幅不同角度的平面标定板图像，计算相机的内参矩阵（K）和外参矩阵（R, t） ，并优化畸变系数（k1, k2, p1, p2, k3）。

1. 标定流程概述

  1. 准备标定板（如棋盘格，已知物理尺寸）。
  2. 拍摄多张不同角度的标定板图像（通常10~20张）。
  3. 检测角点 （corner points）并建立2D-3D对应关系。
  4. 计算单应性矩阵（Homography），建立图像平面与标定板平面的映射关系。
  5. 求解初始内参矩阵（K），利用旋转矩阵的正交性约束。
  6. 优化所有参数 （内参、外参、畸变系数）使用最大似然估计（MLE）或Levenberg-Marquardt算法进行非线性优化。

2. 核心数学原理

2.1 相机模型

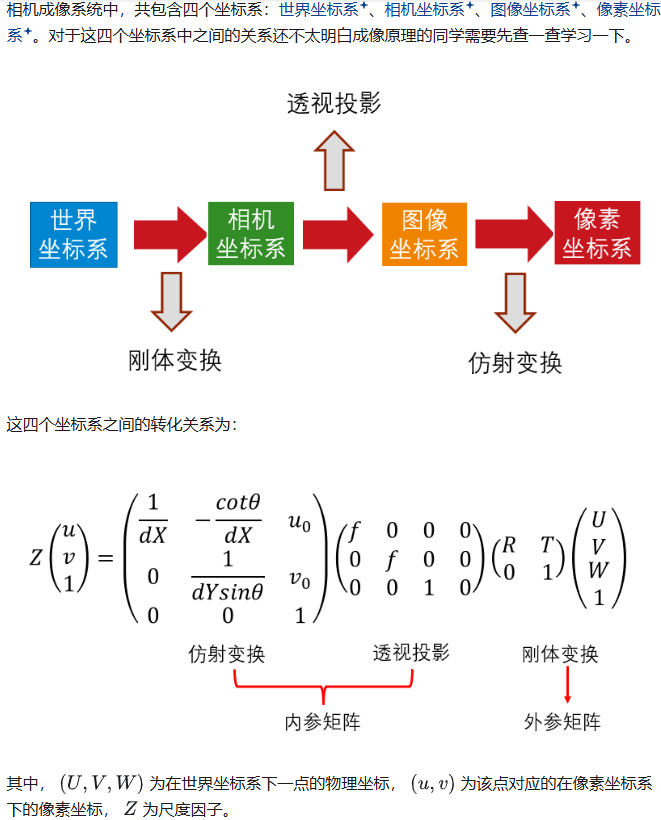
在标定系统中世界坐标系是棋盘格的左上角，由于棋盘格物理尺寸是已知的，因此世界坐标系中的棋盘角点坐标是已知的。（U,V,W=0）.

相机坐标系位于相机光心

图像坐标系位于图像中心

以上三个坐标系都是实际物理尺寸。

像素坐标系是图像左上角为原点，向右为x轴，向下为y轴。多少个像素坐标就是多少。
焦距0.53mm,像素大小 1.4μm,1.4μm, 有效感光面积 1400μm,1400μm, 请问相机内参是多少？

以下是详细计算步骤：

已知参数
  • 焦距（f）：0.53 mm
  • 像素尺寸（dx, dy）：1.4 μm × 1.4 μm （即 0.0014 mm × 0.0014 mm）
  • 有效感光区域：1400 μm × 1400 μm （即 1.4 mm × 1.4 mm）
计算步骤

  1. 计算图像分辨率：

    • 图像宽度（W）= 感光区域宽度 / 像素宽度 = 1400 μm / 1.4 μm = 1000 像素
    • 图像高度（H）= 感光区域高度 / 像素高度 = 1400 μm / 1.4 μm = 1000 像素
    • 因此，图像分辨率是 1000×1000 像素

  2. 计算主点（principal point, cx, cy）：

    • 通常假设主点在图像中心
    • cx = W / 2 = 1000 / 2 = 500
    • cy = H / 2 = 1000 / 2 = 500

  3. 计算焦距的像素单位值（fx, fy）：

    • fx = f / dx = 0.53 mm / 0.0014 mm ≈ 378.57
    • fy = f / dy = 0.53 mm / 0.0014 mm ≈ 378.57
    • （因为像素是正方形，所以 fx ≈ fy）

  4. 构建相机内参矩阵 K：

    复制代码 
    K = [ fx   0   cx ]
    [  0  fy   cy ]
    [  0   0    1 ]

    代入数值：

    复制代码 
    K ≈ [ 378.57     0     500 ]
    [     0   378.57   500 ]
    [     0     0       1   ]
完整相机内参
python 复制代码 
import numpy as np

K = np.array([
    [378.57, 0,     500],
    [0,     378.57, 500],
    [0,     0,       1]
])

相机成像模型（不考虑畸变）：

{ s [ u v 1 ] = K [ R t ] [ X w Y w Z w 1 ] K = [ f x 0 c x 0 f y c y 0 0 1 ] \begin{cases} s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = K \begin{bmatrix} R & t \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix} \\ K = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \end{cases} ⎩ ⎨ ⎧s uv1 =K[Rt] XwYwZw1 K= fx000fy0cxcy1

  • ( X w , Y w , Z w ) (X_w, Y_w, Z_w) (Xw,Yw,Zw)：标定板上的3D点（通常 Z w = 0 Z_w = 0 Zw=0 因为是平面）。
  • ( u , v ) (u, v) (u,v)：图像上的2D像素坐标。
  • K K K：内参矩阵（含焦距 f x , f y f_x, f_y fx,fy、主点 c x , c y c_x, c_y cx,cy）。
  • R , t R, t R,t：外参（旋转矩阵和平移向量）。
  • s s s：尺度因子。

2.2 单应性矩阵（Homography）

由于标定板是平面（ Z w = 0 Z_w = 0 Zw=0），投影方程简化为：

s [ u v 1 ] = K [ r 1 r 2 t ] [ X w Y w 1 ] s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = K \begin{bmatrix} r_1 & r_2 & t \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ 1 \end{bmatrix} s uv1 =K[r1r2t] XwYw1

其中：

  • H = K [ r 1 r 2 t ] H = K \begin{bmatrix} r_1 & r_2 & t \end{bmatrix} H=K[r1r2t] 是 单应性矩阵（3×3）。
  • r 1 , r 2 r_1, r_2 r1,r2 是旋转矩阵 R R R 的前两列（ r 3 = r 1 × r 2 r_3 = r_1 \times r_2 r3=r1×r2）。

求解 H H H：

  • 每张标定板图像可计算一个 H H H（至少需要4个点）。
  • 使用DLT（Direct Linear Transform）或SVD求解。

2.3 约束条件求内参 K K K

根据单应性矩阵 H H H 求解相机内参矩阵 K K K 是张正友标定法的核心步骤。以下是详细的数学推导和计算过程：

2.3.1 单应性矩阵 H H H 的定义

在平面标定（如棋盘格）中，单应性矩阵 H H H 建立了标定板平面（ Z w = 0 Z_w = 0 Zw=0）与图像平面的映射关系：

s [ u v 1 ] = H [ X w Y w 1 ] , H = K [ r 1 r 2 t ] s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = H \begin{bmatrix} X_w \\ Y_w \\ 1 \end{bmatrix}, \quad H = K \begin{bmatrix} r_1 & r_2 & t \end{bmatrix} s uv1 =H XwYw1 ,H=K[r1r2t]

其中：

  • H H H 是 3×3 矩阵， H = [ h 1 h 2 h 3 ] H = \begin{bmatrix} h_1 & h_2 & h_3 \end{bmatrix} H=[h1h2h3]（ h 1 , h 2 , h 3 h_1, h_2, h_3 h1,h2,h3 为列向量）。
  • K K K 是内参矩阵， K = [ f x 0 c x 0 f y c y 0 0 1 ] K = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} K= fx000fy0cxcy1 。
  • r 1 , r 2 r_1, r_2 r1,r2 是旋转矩阵 R R R 的前两列（ r 3 = r 1 × r 2 r_3 = r_1 \times r_2 r3=r1×r2）。
2.3.2 利用旋转矩阵的正交性约束

因为 R R R 是正交矩阵，其列向量满足：

r 1 T r 2 = 0 , ∥ r 1 ∥ = ∥ r 2 ∥ = 1 r_1^T r_2 = 0, \quad \| r_1 \| = \| r_2 \| = 1 r1Tr2=0,∥r1∥=∥r2∥=1

根据 H = K [ r 1 r 2 t ] H = K \begin{bmatrix} r_1 & r_2 & t \end{bmatrix} H=K[r1r2t]，可以表示：

{ r 1 = λ K − 1 h 1 r 2 = λ K − 1 h 2 \begin{cases} r_1 = \lambda K^{-1} h_1 \\ r_2 = \lambda K^{-1} h_2 \\ \end{cases} {r1=λK−1h1r2=λK−1h2

其中 λ \lambda λ 是尺度因子。

将 r 1 , r 2 r_1, r_2 r1,r2 代入正交约束：

{ h 1 T K − T K − 1 h 2 = 0 h 1 T K − T K − 1 h 1 = h 2 T K − T K − 1 h 2 \begin{cases} h_1^T K^{-T} K^{-1} h_2 = 0 \\ h_1^T K^{-T} K^{-1} h_1 = h_2^T K^{-T} K^{-1} h_2 \end{cases} {h1TK−TK−1h2=0h1TK−TK−1h1=h2TK−TK−1h2

2.3.3 定义 B = K − T K − 1 B = K^{-T} K^{-1} B=K−TK−1

令 B = K − T K − 1 B = K^{-T} K^{-1} B=K−TK−1，则 B B B 是一个对称矩阵：

B = [ B 11 B 12 B 13 B 12 B 22 B 23 B 13 B 23 B 33 ] B = \begin{bmatrix} B_{11} & B_{12} & B_{13} \\ B_{12} & B_{22} & B_{23} \\ B_{13} & B_{23} & B_{33} \end{bmatrix} B= B11B12B13B12B22B23B13B23B33

通过 K K K 的结构，可以推导 B B B 的具体形式：

B = K − T K − 1 = [ 1 f x 2 0 − c x f x 2 0 1 f y 2 − c y f y 2 − c x f x 2 − c y f y 2 c x 2 f x 2 + c y 2 f y 2 + 1 ] B = K^{-T} K^{-1} = \begin{bmatrix} \frac{1}{f_x^2} & 0 & -\frac{c_x}{f_x^2} \\ 0 & \frac{1}{f_y^2} & -\frac{c_y}{f_y^2} \\ -\frac{c_x}{f_x^2} & -\frac{c_y}{f_y^2} & \frac{c_x^2}{f_x^2} + \frac{c_y^2}{f_y^2} + 1 \end{bmatrix} B=K−TK−1= fx210−fx2cx0fy21−fy2cy−fx2cx−fy2cyfx2cx2+fy2cy2+1

2.3.4 构建线性方程组

对于每张标定图像， H H H 提供两个约束：

{ h 1 T B h 2 = 0 h 1 T B h 1 = h 2 T B h 2 \begin{cases} h_1^T B h_2 = 0 \\ h_1^T B h_1 = h_2^T B h_2 \end{cases} {h1TBh2=0h1TBh1=h2TBh2

将 B B B 展开为向量 b = [ B 11 , B 12 , B 22 , B 13 , B 23 , B 33 ] T b = [B_{11}, B_{12}, B_{22}, B_{13}, B_{23}, B_{33}]^T b=[B11,B12,B22,B13,B23,B33]T，则约束可写成：

h 11 h 21 h 11 h 22 + h 12 h 21 h 12 h 22 h 13 h 21 + h 11 h 23 h 13 h 22 + h 12 h 23 h 13 h 23 h 11 2 − h 21 2 2 ( h 11 h 12 − h 21 h 22 ) h 12 2 − h 22 2 2 ( h 11 h 13 − h 21 h 23 ) 2 ( h 12 h 13 − h 22 h 23 ) h 13 2 − h 23 2 \] b = 0 \\begin{bmatrix} h_{11} h_{21} \& h_{11} h_{22} + h_{12} h_{21} \& h_{12} h_{22} \& h_{13} h_{21} + h_{11} h_{23} \& h_{13} h_{22} + h_{12} h_{23} \& h_{13} h_{23} \\\\ h_{11}\^2 - h_{21}\^2 \& 2(h_{11} h_{12} - h_{21} h_{22}) \& h_{12}\^2 - h_{22}\^2 \& 2(h_{11} h_{13} - h_{21} h_{23}) \& 2(h_{12} h_{13} - h_{22} h_{23}) \& h_{13}\^2 - h_{23}\^2 \\end{bmatrix} b = 0 \[h11h21h112−h212h11h22+h12h212(h11h12−h21h22)h12h22h122−h222h13h21+h11h232(h11h13−h21h23)h13h22+h12h232(h12h13−h22h23)h13h23h132−h232\]b=0 对于 n n n 张图像，堆叠所有约束得到 2 n × 6 2n \\times 6 2n×6 的矩阵 V V V，求解： V b = 0 V b = 0 Vb=0 ##### **2.3.5 求解 b b b（最小二乘解）** 通过 **SVD分解** V = U Σ W T V = U \\Sigma W\^T V=UΣWT，解 b b b 是 V V V 的右奇异向量对应最小奇异值的列： b = W \[ : , − 1 \] b = W\[:, -1\] b=W\[:,−1

2.3.6 从 B B B 分解出 K K K

已知 B = K − T K − 1 B = K^{-T} K^{-1} B=K−TK−1，通过 Cholesky分解 计算 K − 1 K^{-1} K−1，再求逆得 K K K：

  1. 计算 B B B 的 Cholesky 分解： B = L L T B = L L^T B=LLT。
  2. 则 K − 1 = L T K^{-1} = L^T K−1=LT，因此 K = L − T K = L^{-T} K=L−T。

具体步骤：

c x = − B 13 f x 2 c y = − B 23 f y 2 f x = 1 B 11 f y = 1 B 22 \begin{aligned} c_x &= -B_{13} f_x^2 \\ c_y &= -B_{23} f_y^2 \\ f_x &= \sqrt{\frac{1}{B_{11}}} \\ f_y &= \sqrt{\frac{1}{B_{22}}} \\ \end{aligned} cxcyfxfy=−B13fx2=−B23fy2=B111 =B221

2.3.7 示例计算

假设通过多张图像求得：

B = [ 0.0007 0 − 0.35 0 0.0007 − 0.35 − 0.35 − 0.35 1.245 ] B = \begin{bmatrix} 0.0007 & 0 & -0.35 \\ 0 & 0.0007 & -0.35 \\ -0.35 & -0.35 & 1.245 \end{bmatrix} B= 0.00070−0.3500.0007−0.35−0.35−0.351.245

则：

f x = 1 / 0.0007 ≈ 37.8 f y = 1 / 0.0007 ≈ 37.8 c x = − ( − 0.35 ) × 37. 8 2 ≈ 500 c y = − ( − 0.35 ) × 37. 8 2 ≈ 500 \begin{aligned} f_x &= \sqrt{1 / 0.0007} \approx 37.8 \\ f_y &= \sqrt{1 / 0.0007} \approx 37.8 \\ c_x &= -(-0.35) \times 37.8^2 \approx 500 \\ c_y &= -(-0.35) \times 37.8^2 \approx 500 \\ \end{aligned} fxfycxcy=1/0.0007 ≈37.8=1/0.0007 ≈37.8=−(−0.35)×37.82≈500=−(−0.35)×37.82≈500

最终内参矩阵：

K = [ 37.8 0 500 0 37.8 500 0 0 1 ] K = \begin{bmatrix} 37.8 & 0 & 500 \\ 0 & 37.8 & 500 \\ 0 & 0 & 1 \end{bmatrix} K= 37.800037.805005001

2.3.8 总结步骤
  1. 计算单应性矩阵 H H H （每张图像一个 H H H）。
  2. 构建约束矩阵 V V V 并求解 b b b（SVD分解）。
  3. 恢复 B = K − T K − 1 B = K^{-T} K^{-1} B=K−TK−1。
  4. Cholesky分解 B B B 得到 K − 1 K^{-1} K−1，再求逆得 K K K。
  5. 优化（Bundle Adjustment）提高精度。

这种方法仅需平面标定板，即可高效求解相机内参，是张正友标定法的核心贡献。

2.4 求解外参 R , t R, t R,t

一旦 K K K 已知，外参可通过 H H H 计算：
{ r 1 = λ K − 1 h 1 r 2 = λ K − 1 h 2 r 3 = r 1 × r 2 t = λ K − 1 h 3 \begin{cases} r_1 = \lambda K^{-1} h_1 \\ r_2 = \lambda K^{-1} h_2 \\ r_3 = r_1 \times r_2 \\ t = \lambda K^{-1} h_3 \end{cases} ⎩ ⎨ ⎧r1=λK−1h1r2=λK−1h2r3=r1×r2t=λK−1h3

其中 λ = 1 / ∥ K − 1 h 1 ∥ \lambda = 1 / \| K^{-1} h_1 \| λ=1/∥K−1h1∥。

2.5 畸变校正

张正友标定法（Zhang's Method）通过棋盘格标定同时求解相机内参（包括焦距、主点）和畸变系数（径向畸变 k 1 , k 2 , k 3 k_1, k_2, k_3 k1,k2,k3 和切向畸变 p 1 , p 2 p_1, p_2 p1,p2），其核心原理分为以下几个关键步骤：

2.5.1 基本假设与模型
相机成像模型

  • 理想针孔模型（无畸变）：

    s [ u v 1 ] = K [ R t ] [ X w Y w Z w 1 ] , K = [ f x 0 c x 0 f y c y 0 0 1 ] s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = K \begin{bmatrix} R & t \end{bmatrix} \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix}, \quad K = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} s uv1 =K[Rt] XwYwZw1 ,K= fx000fy0cxcy1

    其中 ( X w , Y w , Z w ) (X_w, Y_w, Z_w) (Xw,Yw,Zw) 是世界坐标， ( u , v ) (u, v) (u,v) 是像素坐标。

  • 引入畸变（实际成像）：

    • 径向畸变： x dist = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) x_{\text{dist}} = x (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) xdist=x(1+k1r2+k2r4+k3r6)
    • 切向畸变： x dist + = 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) x_{\text{dist}} += 2 p_1 x y + p_2 (r^2 + 2 x^2) xdist+=2p1xy+p2(r2+2x2)
    • 其中 r 2 = x 2 + y 2 r^2 = x^2 + y^2 r2=x2+y2， ( x , y ) (x, y) (x,y) 是归一化坐标（ x = ( u − c x ) / f x x = (u - c_x)/f_x x=(u−cx)/fx）。
平面约束

标定板平面满足 Z w = 0 Z_w = 0 Zw=0，因此单应性矩阵 H H H 可建立图像与标定板的映射：

s [ u v 1 ] = H [ X w Y w 1 ] , H = K [ r 1 r 2 t ] s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = H \begin{bmatrix} X_w \\ Y_w \\ 1 \end{bmatrix}, \quad H = K \begin{bmatrix} r_1 & r_2 & t \end{bmatrix} s uv1 =H XwYw1 ,H=K[r1r2t]

2.5.2 求解畸变系数的核心原理
单应性矩阵估计

对每张标定图像：

  1. 检测棋盘格角点的像素坐标 ( u , v ) (u, v) (u,v) 和对应的世界坐标 ( X w , Y w , 0 ) (X_w, Y_w, 0) (Xw,Yw,0)。
  2. 通过 直接线性变换（DLT） 或 最小二乘法 求解单应性矩阵 H H H。
内参约束

利用旋转矩阵 R R R 的正交性（ r 1 T r 2 = 0 r_1^T r_2 = 0 r1Tr2=0, ∥ r 1 ∥ = ∥ r 2 ∥ = 1 \|r_1\| = \|r_2\| = 1 ∥r1∥=∥r2∥=1），从 H H H 推导内参矩阵 K K K：

{ h 1 T K − T K − 1 h 2 = 0 h 1 T K − T K − 1 h 1 = h 2 T K − T K − 1 h 2 \begin{cases} h_1^T K^{-T} K^{-1} h_2 = 0 \\ h_1^T K^{-T} K^{-1} h_1 = h_2^T K^{-T} K^{-1} h_2 \end{cases} {h1TK−TK−1h2=0h1TK−TK−1h1=h2TK−TK−1h2

通过多张图像的 H H H 构建线性方程组，求解对称矩阵 B = K − T K − 1 B = K^{-T} K^{-1} B=K−TK−1，再通过 Cholesky分解 得到 K K K。

畸变系数求解

在获得初始内参 K K K 和外参 R , t R, t R,t 后：

  1. 重投影误差最小化：将标定板的3D点投影到图像，与实际检测的角点比较。

  2. 非线性优化（如Levenberg-Marquardt算法）优化以下目标函数：

    min ⁡ K , k , p , R , t ∑ i = 1 n ∑ j = 1 m ∥ p i j − p ^ ( K , k , p , R i , t i , P j ) ∥ 2 \min_{K, k, p, R, t} \sum_{i=1}^{n} \sum_{j=1}^{m} \| p_{ij} - \hat{p}(K, k, p, R_i, t_i, P_j) \|^2 K,k,p,R,tmini=1∑nj=1∑m∥pij−p^(K,k,p,Ri,ti,Pj)∥2

    • p i j p_{ij} pij：第 i i i 张图像中第 j j j 个角点的实际像素坐标。
    • p ^ \hat{p} p^：根据当前参数计算的投影坐标（含畸变模型）。
    • k = [ k 1 , k 2 , k 3 ] k = [k_1, k_2, k_3] k=[k1,k2,k3]， p = [ p 1 , p 2 ] p = [p_1, p_2] p=[p1,p2]：待优化的畸变系数。
2.5.3 畸变系数的物理意义
系数 类型 物理意义 影响区域
k 1 k_1 k1 径向畸变 主导桶形（负值）或枕形（正值）畸变 图像中心及边缘
k 2 k_2 k2 径向畸变 修正高阶畸变 边缘更显著
p 1 p_1 p1 切向畸变 镜头与传感器不平行导致的倾斜畸变 整体图像
p 2 p_2 p2 切向畸变 镜头与传感器不平行导致的扭曲畸变 整体图像
k 3 k_3 k3 径向畸变 广角镜头的大范围畸变修正 边缘区域
2.5.4 关键数学推导
畸变模型的线性化近似

初始阶段，忽略高阶畸变（设 k 3 = 0 k_3 = 0 k3=0, p 1 = p 2 = 0 p_1 = p_2 = 0 p1=p2=0），仅用 k 1 , k 2 k_1, k_2 k1,k2 简化计算。在非线性优化阶段逐步引入所有系数。

重投影误差计算

对于每个角点，计算畸变后的投影坐标：

u ′ v ′ \] = distort ( K \[ R t \] \[ X w Y w 0 1 \] , k , p ) \\begin{bmatrix} u' \\\\ v' \\end{bmatrix} = \\text{distort}\\left( K \\begin{bmatrix} R \& t \\end{bmatrix} \\begin{bmatrix} X_w \\\\ Y_w \\\\ 0 \\\\ 1 \\end{bmatrix}, k, p \\right) \[u′v′\]=distort K\[Rt\] XwYw01 ,k,p 误差项为： e = ∥ \[ u v \] − \[ u ′ v ′ \] ∥ 2 e = \\\| \\begin{bmatrix} u \\\\ v \\end{bmatrix} - \\begin{bmatrix} u' \\\\ v' \\end{bmatrix} \\\|\^2 e=∥\[uv\]−\[u′v′\]∥2 ###### **非线性优化** 通过迭代优化（如OpenCV的 `cv2.calibrateCamera`）联合调整所有参数，使总重投影误差最小。 ##### **2.5.5 实验验证** ###### **标定结果示例** ```python # OpenCV标定输出示例 dist_coeffs = np.array([k1, k2, p1, p2, k3]) # 畸变系数 camera_matrix = np.array([[fx, 0, cx], [0, fy, cy], [0, 0, 1]]) # 内参矩阵 ``` * **典型值范围** ： * k 1 k_1 k1: \[-0.2, 0.2

  • p 1 , p 2 p_1, p_2 p1,p2: [-0.001, 0.001]
验证方法
  • 重投影误差：应小于0.5像素。
  • 可视化校正 ：使用 cv2.undistort 观察校正后图像是否去除畸变。
2.5.6 为什么能同时求解内参和畸变？
  1. 分阶段求解 ：
    • 先假设无畸变，用单应性矩阵求初始内参和外参。
    • 再用初始参数估计畸变，最后联合优化所有参数。
  2. 多约束条件 ：
    • 多张图像的棋盘格提供大量冗余方程，确保方程可解。
  3. 非线性优化 ：
    • 通过迭代逐步逼近最优解，避免直接求解复杂非线性方程。
2.5.7 总结

张正友标定法通过平面标定板的2D-3D对应关系 ，结合旋转矩阵约束 和非线性优化，同时求解内参和畸变系数。其优势在于：

  • 仅需平面标定板，无需复杂设备。
  • 同时估计径向和切向畸变，适用大多数镜头。
  • 开放源码实现（如OpenCV）使其成为工业标准方法。

3. 优化（Bundle Adjustment）

初始解可能不够精确，因此采用非线性优化 （如Levenberg-Marquardt算法）最小化重投影误差：

min ⁡ K , R , t , k ∑ i = 1 n ∑ j = 1 m ∥ p i j − p ^ ( K , R i , t i , k , P j ) ∥ 2 \min_{K, R, t, k} \sum_{i=1}^{n} \sum_{j=1}^{m} \| p_{ij} - \hat{p}(K, R_i, t_i, k, P_j) \|^2 K,R,t,kmini=1∑nj=1∑m∥pij−p^(K,Ri,ti,k,Pj)∥2

  • p i j p_{ij} pij：观测到的第 j j j 个点在图像 i i i 中的位置。
  • p ^ \hat{p} p^：根据当前参数计算的重投影点。

4. 算法总结

步骤 任务 方法
1 检测角点 Harris角点检测或亚像素优化
2 计算单应性矩阵 H H H DLT + SVD
3 求解内参 K K K 利用正交约束 + Cholesky分解
4 计算外参 R , t R, t R,t R = [ r 1 , r 2 , r 1 × r 2 ] R = [r_1, r_2, r_1 \times r_2] R=[r1,r2,r1×r2]
5 估计畸变系数 线性最小二乘
6 非线性优化 Bundle Adjustment

优点

✅ 只需要平面标定板（如棋盘格），无需精密3D标定设备。

✅ 计算高效，适合普通相机和手机摄像头标定。

✅ 可同时估计内参、外参和畸变系数。

缺点

❌ 标定板必须足够平整，否则影响精度。

❌ 需要多张不同角度的图像（通常≥10张）。

5. 实际应用（OpenCV示例）

通过张正友标定法（棋盘格标定）获取径向畸变系数（ k 1 , k 2 , k 3 k_1, k_2, k_3 k1,k2,k3）和切向畸变系数（ p 1 , p 2 p_1, p_2 p1,p2）的完整流程如下：

5.1 准备标定板

  • 使用已知尺寸的棋盘格（如每格10mm×10mm），黑白方格需具有高对比度。
  • 棋盘格角点数建议不少于 6×9（OpenCV要求角点数至少为内角点，即行列数减1）。

5.2 采集多角度标定图像

  • 拍摄 10~20张 不同角度、位置的棋盘格图像（覆盖图像边缘和中心）。
  • 确保标定板在图像中完整可见，避免过曝或模糊。

5.3 检测角点并建立2D-3D对应关系

代码实现（OpenCV）
python 复制代码 
import cv2
import numpy as np
import glob

# 定义棋盘格内角点数量（行列数减1）
pattern_size = (8, 6)  # 例如9x7的棋盘格，内角点为8x6

# 准备3D世界坐标 (Z=0)
objp = np.zeros((pattern_size[0] * pattern_size[1], 3), np.float32)
objp[:, :2] = np.mgrid[0:pattern_size[0], 0:pattern_size[1]].T.reshape(-1, 2)

# 存储3D-2D对应点
objpoints = []  # 世界坐标
imgpoints = []  # 图像坐标

# 读取标定图像
images = glob.glob('calib_images/*.jpg')
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    
    # 查找角点
    ret, corners = cv2.findChessboardCorners(gray, pattern_size, None)
    
    if ret:
        # 亚像素精确化（提高角点精度）
        corners_refined = cv2.cornerSubPix(
            gray, corners, (11, 11), (-1, -1),
            criteria=(cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
        )
        
        objpoints.append(objp)
        imgpoints.append(corners_refined)
        
        # 可视化角点（可选）
        cv2.drawChessboardCorners(img, pattern_size, corners_refined, ret)
        cv2.imshow('Corners', img)
        cv2.waitKey(500)

cv2.destroyAllWindows()

5.4 标定相机并获取畸变系数

调用OpenCV标定函数
python 复制代码 
# 执行标定
ret, camera_matrix, dist_coeffs, rvecs, tvecs = cv2.calibrateCamera(
    objpoints, imgpoints, gray.shape[::-1], None, None
)

# 输出结果
print("相机内参矩阵 K:\n", camera_matrix)
print("畸变系数 (k1, k2, p1, p2, k3):\n", dist_coeffs)

  • 输出示例 ：

    复制代码 
    畸变系数: [k1, k2, p1, p2, k3] = [-0.1, 0.01, 0.001, -0.001, 0.0]
    • k1, k2, k3：径向畸变系数（通常 k 3 k_3 k3 对小畸变镜头可忽略）。
    • p1, p2：切向畸变系数。

5.5 验证标定结果

重投影误差
python 复制代码 
# 计算重投影误差
mean_error = 0
for i in range(len(objpoints)):
    imgpoints_repro, _ = cv2.projectPoints(
        objpoints[i], rvecs[i], tvecs[i], camera_matrix, dist_coeffs
    )
    error = cv2.norm(imgpoints[i], imgpoints_repro, cv2.NORM_L2) / len(imgpoints_repro)
    mean_error += error

print("平均重投影误差 (像素):", mean_error / len(objpoints))
  • 误差要求 ：一般应 < 0.5像素，若误差过大需检查标定图像质量或角点检测。

5.6 畸变系数详解

系数 类型 物理意义 典型值范围
k 1 k_1 k1 径向畸变 主导桶形/枕形畸变 [-0.2, 0.2]
k 2 k_2 k2 径向畸变 高阶修正项 [-0.05, 0.05]
p 1 p_1 p1 切向畸变 由镜头-传感器不平行引起 [-0.001, 0.001]
p 2 p_2 p2 切向畸变 由镜头-传感器不平行引起 [-0.001, 0.001]
k 3 k_3 k3 径向畸变 广角镜头需启用 [-0.1, 0.1]

5.7 注意事项

  1. 标定板覆盖范围：

    • 确保标定板覆盖图像的 边缘和中心，否则边缘畸变系数可能不准确。

  2. 图像数量：

    • 至少 10张，建议15~20张不同角度。

  3. 标定板平整度：

    • 棋盘格必须完全平整，弯曲会导致标定误差。

  4. 光照均匀性：

    • 避免反光或阴影影响角点检测。

  5. 鱼眼镜头：

    • 需改用 cv2.fisheye.calibrate，畸变模型不同。

5.8 完整代码示例

python 复制代码 
import cv2
import numpy as np
import glob


# https://developer.aliyun.com/article/1599339
if __name__ == "__main__":
        
    # 定义棋盘格内角点数量（行列数减1）
    pattern_size = (9, 9)  # 例如9x7的棋盘格，内角点为8x6

    # 准备3D世界坐标 (Z=0)
    objp = np.zeros((pattern_size[0] * pattern_size[1], 3), np.float32)
    objp[:, :2] = np.mgrid[0:pattern_size[0], 0:pattern_size[1]].T.reshape(-1, 2) * 5 # 5mm

    # 存储3D-2D对应点
    objpoints = []  # 世界坐标
    imgpoints = []  # 图像坐标

    # 读取标定图像
    images = glob.glob('calib/*.tif')
    for fname in images:
       
        img = cv2.imread(fname)
        gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        gray = cv2.blur(gray, (5, 5))
        # 查找角点
        ret, corners = cv2.findChessboardCorners(gray, pattern_size, None)
        print(fname,ret)
        if ret:
            # 亚像素精确化（提高角点精度）
            corners_refined = cv2.cornerSubPix(
                gray, corners, (11, 11), (-1, -1),
                criteria=(cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
            )
            
            objpoints.append(objp)
            imgpoints.append(corners_refined)
            
            # 可视化角点（可选）
            cv2.drawChessboardCorners(img, pattern_size, corners_refined, ret)
            cv2.imwrite(fname.replace('.tif', '_calib.png'), img)



    # 执行标定
    ret, camera_matrix, dist_coeffs, rvecs, tvecs = cv2.calibrateCamera(
        objpoints, imgpoints, gray.shape[::-1], None, None
    )

    # 输出结果
    print("相机内参矩阵 K:\n", camera_matrix)
    print("畸变系数 (k1, k2, p1, p2, k3):\n", dist_coeffs)

    
    # 计算重投影误差
    mean_error = 0
    for i in range(len(objpoints)):
        imgpoints_repro, _ = cv2.projectPoints(
            objpoints[i], rvecs[i], tvecs[i], camera_matrix, dist_coeffs
        )
        error = cv2.norm(imgpoints[i], imgpoints_repro, cv2.NORM_L2) / len(imgpoints_repro)
        mean_error += error

    print("平均重投影误差 (像素):", mean_error / len(objpoints))

通过以上步骤，即可准确获取径向和切向畸变系数，后续可通过 cv2.undistort() 进行图像校正。

6. 总结

张正友标定法通过平面标定板 和多视角约束，高效计算相机参数，是计算机视觉中最常用的标定方法之一。其核心在于：

  1. 单应性矩阵 建立2D-3D映射。
  2. 正交约束 求解内参。
  3. 非线性优化 提高精度。
热门推荐
01Cursor Claude 模型无法使用的解决方法02全球最强模型Grok4，国内已可免费使用！（附教程）03KGG转MP3工具|非KGM文件|解密音频04Cursor如何配置代理05【无标题】06Coze扣子平台完整体验和实践（附国内和国际版对比）07《深入设计模式》模式结构汇总08绿色建筑新态势：楼宇自控助力能效提升，推动成本优化新路径09扣子（coze）实战|我用扣子搭建了一个自动分析小红薯笔记内容的AI应用|详细步骤拆解10（5千字总结）国内如何安装和使用 Claude Code 的保姆级教程 - 支持Mac和Windows用户