TGRS2023 基于小波池化和图增强分类的无人机小目标跟踪

Virgil1392025-07-17 10:04

收录于TGRS2023 (2023 IEEE Transactions on Geoscience and Remote Sensing )
基于小波池化和图增强分类的无人机小目标跟踪

本文提出了一个基于孪生神经网络的航空跟踪器（SmallTrack），该框架通过小波池化层和图增强模块，显著提升了模型在复杂航空场景中精确跟踪小目标的能力，同时保持了72.5帧/秒的高速运行速度。

该研究基于视频序列进行目标跟踪。实验所使用的数据集（如 UAV20L、UAVDT、DTB70 等）均为包含连续视频帧的 aerial 视频数据集。

文章目录

一、摘要Abstract

Aerial object tracking has shown great potential in the field of remote sensing recently. Nevertheless, small objects that frequently appear in unmanned aerial vehicles (UAVs) scenes have weak appearances and are vulnerable to distractions, posing a huge challenge to aerial trackers. Despite the significant improvements, it is challenging for most trackers to capture enough discriminative features, which becomes even more evident in unavoidable situations involving high altitude and background disturbances. To address the problem of small object tracking for UAVs, we propose a simple yet efficient tracker (SmallTrack) based on the siamese network to improve the discrimination of small objects from two stages. First, the wavelet pooling layer is introduced to remove noises and to avoid aliasing effects via wavelet domain learning, significantly preserving structure and detail information of small objects. Then, the graph enhanced module in classification is designed to exploit potential relations between nodes and to enhance the understanding of targets, which provides cleaner classification responses and makes small objects highly discriminative. To evaluate the performance of proposed tracker, comprehensive experiments are conducted on four challenging aerial tracking benchmarks, including UAV20L, UAVDT, DTB70 and VisDrone2019. Experiment results demonstrate that the proposed tracker achieves leading tracking performance in aerial benchmarks with a mean speed of 72.5 frames/s. In addition, we conducted experiments on the small object dataset, LaTOT, to further verify the effectiveness of our tracker. Moreover, real-world tests onboard a typical embedded platform demonstrate that SmallTrack achieves reliable tracking results with acceptable speed. The tracking demos and code are available at https://github.com/xyl-507/SmallTrack.

Index Terms---Remote sensing, aerial tracking, siamese neural network, wavelet pooling layer, graph enhanced classification.

摘要翻译：

  • 近年来，空中目标跟踪在遥感领域展现出巨大潜力。然而，无人机（UAV）场景中频繁出现的小目标外观特征微弱且易受干扰，这对空中跟踪器构成了巨大挑战。尽管现有方法已取得显著进步，但大多数跟踪器仍难以捕捉足够的判别性特征，这一问题在高空拍摄和背景干扰等不可避免的场景中尤为突出。

  • 为解决无人机小目标跟踪问题，本文提出一种基于孪生网络的简单高效跟踪器（SmallTrack），从两个阶段提升小目标的判别能力：首先，引入小波池化层，通过小波域学习去除噪声并避免混叠效应，显著保留小目标的结构和细节信息；其次，在分类阶段设计图增强模块，挖掘节点间的潜在关系并增强对目标的理解，从而提供更清晰的分类响应，使小目标具有高度判别性。

  • 为评估所提跟踪器的性能，我们在四个具有挑战性的空中跟踪基准数据集（UAV20L、UAVDT、DTB70和VisDrone2019）上进行了全面实验。结果表明，该跟踪器在这些空中基准数据集上实现了领先的跟踪性能，平均速度达72.5帧/秒。此外，我们在小目标数据集LaTOT上进行的实验进一步验证了跟踪器的有效性。同时，在典型嵌入式平台上的实测试验表明，SmallTrack能够以可接受的速度实现可靠的跟踪结果。跟踪演示和代码可在https://github.com/xyl-507/SmallTrack获取。

  • 关键词 ------ 遥感、空中跟踪、孪生神经网络、小波池化层、图增强分类

二、本文贡献总结:

  1. 基于孪生网络的高效跟踪框架：SmallTrack采用孪生网络架构，包含模板分支与搜索分支，通过计算目标模板与搜索区域的互相关相似度实现视觉目标跟踪，将跟踪问题转化为相似性匹配任务，为小目标跟踪提供了高效的基础框架。

  2. 小波池化层（WPL）的提出：设计小波池化层替代传统池化操作，通过二维离散小波变换（2D DWT）将特征图分解为低频（LL）和高频（LH、HL、HH）分量，在实现降采样的同时，有效抑制噪声和混叠效应，充分保留小目标的结构与细节信息，提升了对弱特征小目标的表征能力。

  3. 图增强模块（GEM）的设计：提出基于图神经网络（GNN）的图增强模块，将分类响应图建模为节点（像素）和边（像素关系）的图结构，通过更新节点与边的权重，增强小目标区域的激活响应并抑制背景干扰，显著提升了小目标的判别性。

三、孪生网络Siamese Trackers

A. The Architecture of Siamese Trackers

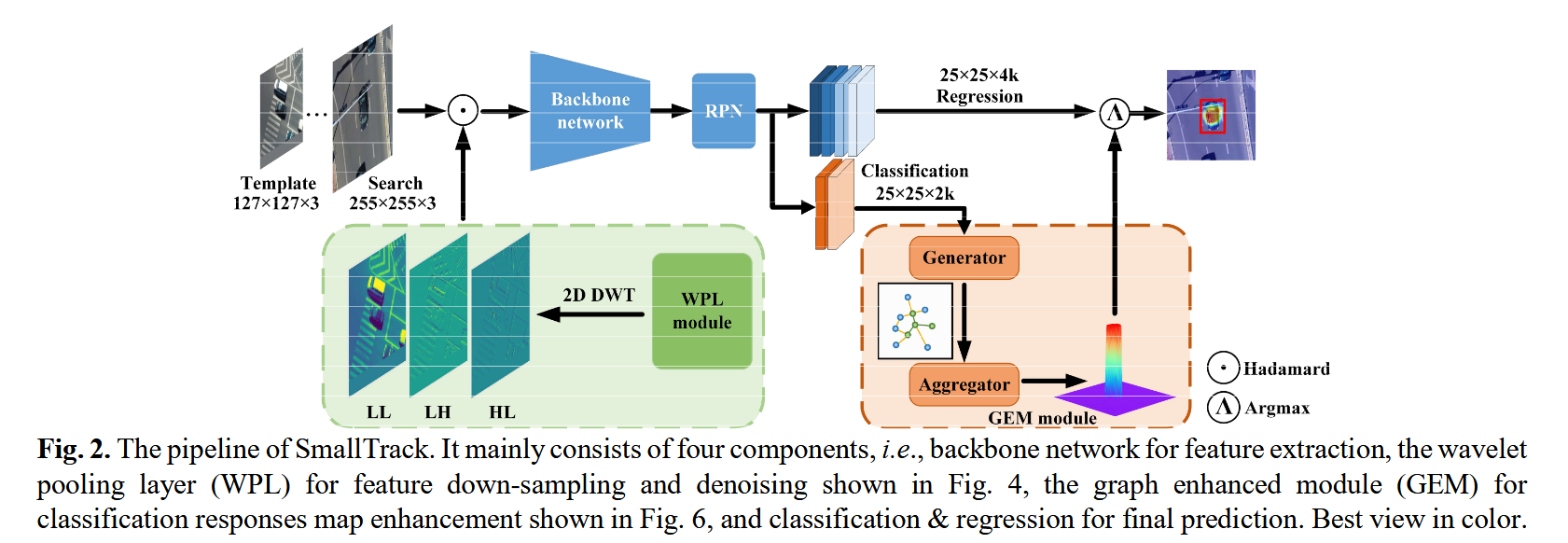
图2: SmallTrack由五个组件组成，用于特征下采样和去噪的WPL，用于特征提取的主干网络，用于相似性响应的交叉相关性，用于分类响应增强的GEM，以及用于最终预测的分类和回归。

孪生网络（Siamese Trackers）架构的核心是将目标跟踪问题转化为相似性匹配任务，通过模板与搜索区域的特征比对实现目标定位。

  1. 核心目标 视觉目标跟踪的核心是最小化目标位置预测与标注标签的残差，优化目标定位，其目标函数如公式（1）所示： L ( ω ) = ∑ j = 1 m γ j r ( f ( x j ; ω ) , y j ) + ∑ k λ k ∥ ω k ∥ 2 (1) L(\omega) = \sum_{j=1}^{m} \gamma_{j} r\left(f\left(x_{j} ; \omega\right), y_{j}\right) + \sum_{k} \lambda_{k}\left\| \omega_{k}\right\| ^{2} \tag{1} L(ω)=j=1∑mγjr(f(xj;ω),yj)+k∑λk∥ωk∥2(1) 其中， f ( x j ; ω ) f(x_{j} ; \omega) f(xj;ω)为每个位置的预测值， y j y_j yj为标注标签， r r r为残差项， γ j \gamma_j γj为影响因子， λ k \lambda_k λk为正则化系数，用于优化模型参数 ω \omega ω。

  2. 网络结构与工作流程 孪生网络包含模板分支（template branch） 和搜索分支（search branch） ： - 模板分支：处理第一帧中人工标注的目标区域（模板 z z z），通过骨干网络 ϕ \phi ϕ提取特征 ϕ ( z ) \phi(z) ϕ(z)； - 搜索分支：处理后续帧中以历史跟踪结果为中心裁剪的固定大小搜索区域（ x x x），提取特征 ϕ ( x ) \phi(x) ϕ(x)。

  3. 相似性计算 通过计算模板特征与搜索区域特征的互相关（cross-correlation）生成响应图，响应值最高的位置即为目标所在，如公式（2）所示： f ( z , x ) = f ( ϕ ( z ) , ϕ ( x ) ) = ϕ ( z ) ∗ ϕ ( x ) + b ⋅ I (2) f(z, x) = f(\phi(z), \phi(x)) = \phi(z) * \phi(x) + b \cdot I \tag{2} f(z,x)=f(ϕ(z),ϕ(x))=ϕ(z)∗ϕ(x)+b⋅I(2) 其中， ∗ * ∗表示互相关运算， b b b为卷积层偏置， I I I为单位矩阵， b ⋅ I b \cdot I b⋅I表示每个位置的偏置信号。 该架构通过滑动窗口式的特征匹配，实现了高效的目标定位，为后续小波池化层（WPL）和图增强模块（GEM）的集成提供了基础框架。

四、小波池化层WPL

WPL计算步骤概括

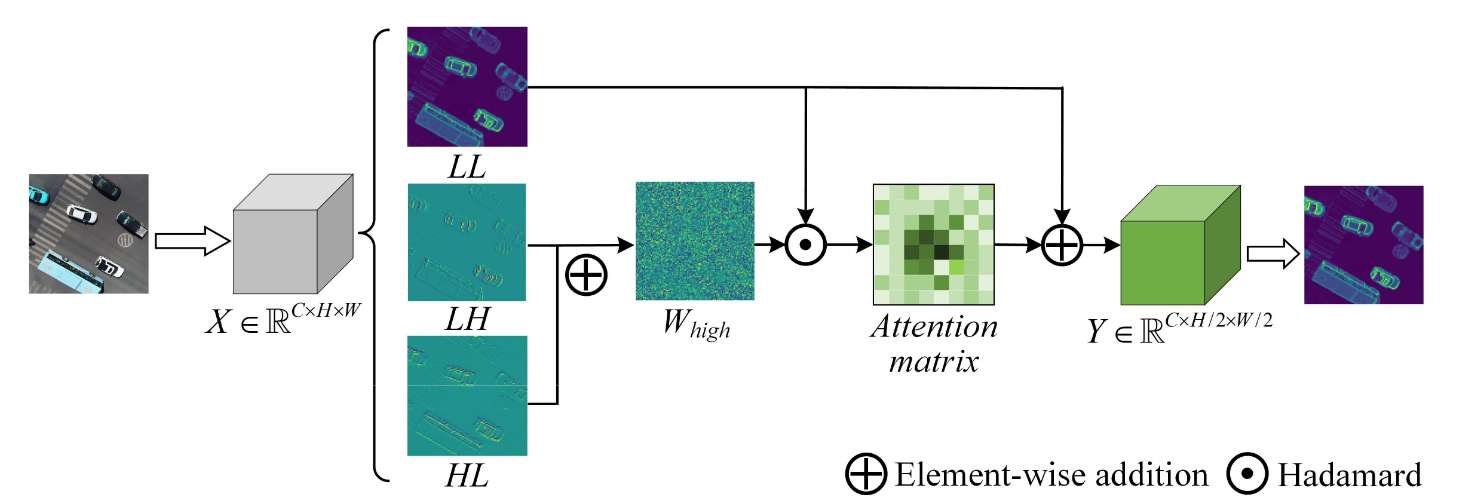
  1. 子带分解 ：通过二维离散小波变换（2D DWT）将输入特征图 X X X分解为四个子带 L L LL LL（低频）、 L H LH LH（水平低频+垂直高频）、 H L HL HL（水平高频+垂直低频）、 H H HH HH（高频），丢弃噪声较多的 H H HH HH。
  2. 高频权重生成 ：将 L H LH LH与 H L HL HL逐元素相加，经softmax归一化生成高频权重 W high W_{\text{high}} Whigh。
  3. 注意力调制 ：将 W high W_{\text{high}} Whigh与 L L LL LL进行哈达玛积运算，得到注意力矩阵 A t t Att Att。
  4. 特征融合 ：将 A t t Att Att与 L L LL LL逐元素相加，得到加权特征 Y Y Y，完成下采样并保留小目标信息。

相关概念解释

  • 离散小波变换：一种将信号分解为不同频率分量（低频近似和高频细节）的数学工具，通过离散化的尺度和位移参数实现。
  • 离散小波子带：信号经离散小波变换后得到的低频（LL）和高频（LH、HL、HH）分量集合，分别对应不同方向的结构和细节信息。
  • 尺度和位移 ：尺度（ a a a）控制小波函数的拉伸/压缩（决定频率高低），位移（ b b b）控制小波函数的平移（决定时间/空间位置）。
  • 基本小波函数 ：构成小波变换基础的函数（ ψ \psi ψ），通过缩放和平移生成一系列小波，用于捕捉信号的局部特征。
  • 希尔伯特空间：一种完备的内积空间，为小波函数的分解（如分为尺度函数和小波函数）提供数学框架。
  • 尺度函数 ：对应信号低频部分的函数（ φ \varphi φ），用于捕捉信号的整体趋势和主要结构。
  • 小波函数 ：对应信号高频部分的函数（ ψ \psi ψ），用于捕捉信号的局部细节和边缘特征。

原文：C. Robust Learning via Wavelet Pooling Layer 基于小波池化层的鲁棒学习

池化通过丢弃部分信息实现下采样，两种常用的池化方式为最大池化和平均池化，其定义分别如公式（3）和公式（4）所示：
a i , j = max ⁡ R i , j ( a R i , j ) a i , j = 1 ∣ R i , j ∣ ∑ R i , j a R i , j \begin{equation} a_{i,j} = \max_{R_{i,j}} \left(a_{R_{i,j}}\right) \tag{3} \end{equation} \\ \begin{equation} a_{i,j} = \frac{1}{|R_{i,j}|} \sum_{R_{i,j}} a_{R_{i,j}} \tag{4} \end{equation} ai,j=Ri,jmax(aRi,j)(3)ai,j=∣Ri,j∣1Ri,j∑aRi,j(4)

其中， i , j i,j i,j 表示特征图上的位置， R i , j R_{i,j} Ri,j 是以 i , j i,j i,j 为中心的池化区域。

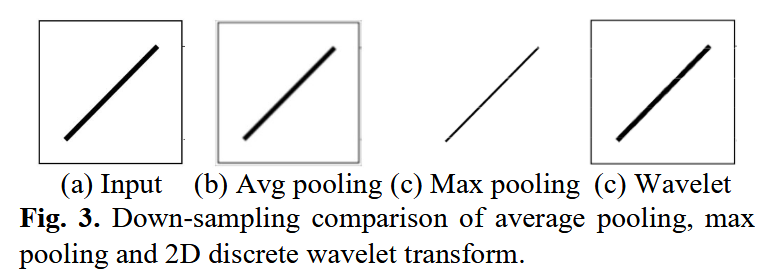
然而，如图3所示，最大池化和平均池化均存在局限性：会产生混叠效应、破坏目标基本结构并放大随机噪声[46]。例如，当主要特征的数值低于非重要特征时，最大池化会丢弃主要特征；而平均池化在整合高值特征和低值特征时，会稀释高值特征的作用[45]。显然，这些常用的池化操作并不适用于小目标跟踪------由于无人机视角下背景 clutter 更多，且小目标的特征信息本身较弱，池化后小目标的特征信息容易被背景噪声淹没。

小波池化被视为这两种主流池化方法的替代方案。在文献[44-46]中，高频分量通常被当作噪声丢弃，仅利用低频分量保留目标的主要信息。但 Wang 等人[61]发现，高频分量包含的信息远超样本特异性特征，在描述某些目标（尤其是小目标）时发挥重要作用。此外，文献[55]探索了双树复小波变换（DT-CWT）在目标跟踪中的应用，但仅将其用于数据预处理。因此，为确保小目标信息不丢失，我们进一步采用离散小波变换（DWT）进行特征提取，同时利用低频分量和高频分量来表征目标。基于文献[46,47]，我们提出小波池化层（WPL）用于特征下采样（如图4所示），同时有效减轻混叠效应和噪声干扰。

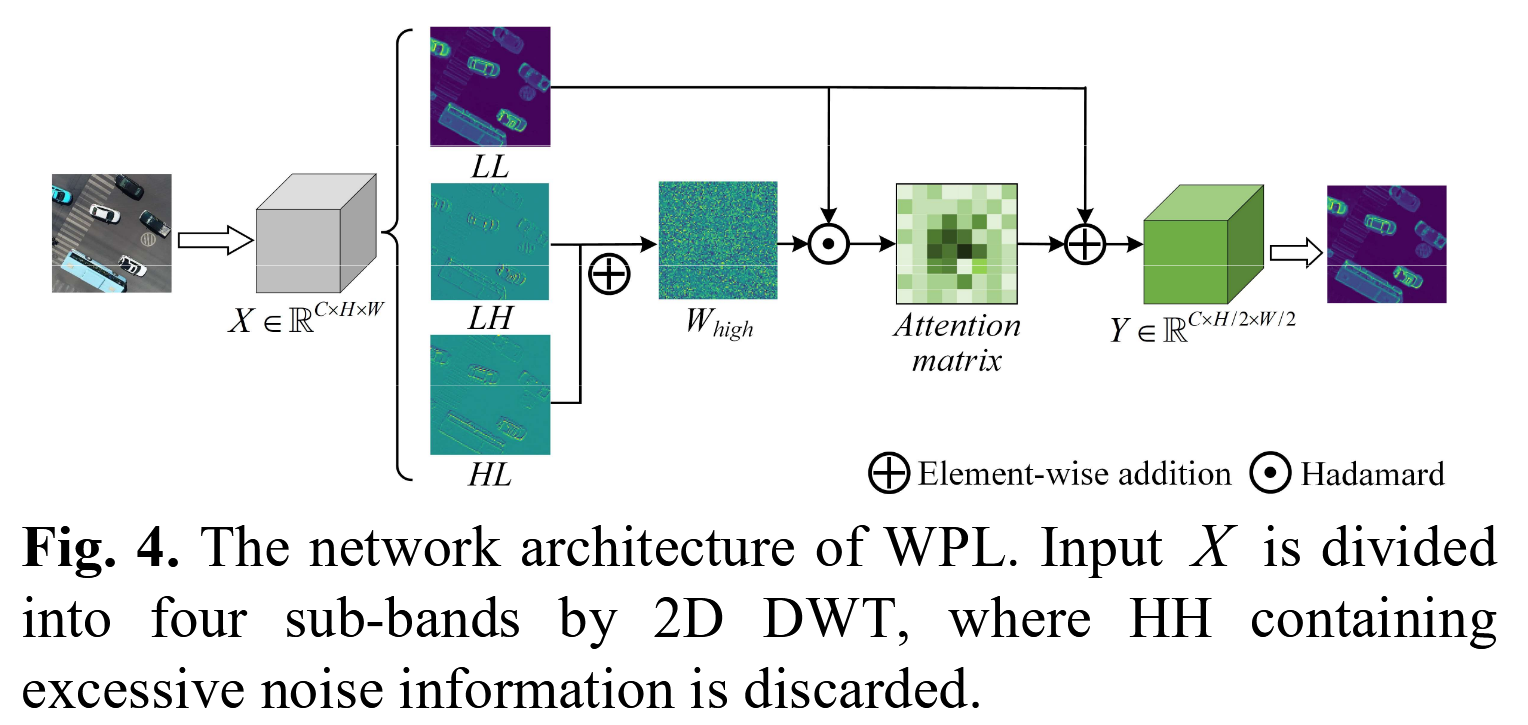
图4. WPL的网络架构。输入X通过二维DWT被分为四个子带，其中包含过多噪声信息的HH被丢弃。

离散小波变换将输入图像分解为四个离散小波子带，其原理如下[62]：

ψ α , b ( t ) = 1 a ∑ n ψ ( t − b a ) (5) \psi_{\alpha,b}(t) = \frac{1}{\sqrt{a}} \sum_{n} \psi\left(\frac{t-b}{a}\right) \tag{5} ψα,b(t)=a 1n∑ψ(at−b)(5)

其中， a a a 和 b b b 分别表示尺度和位移； ψ \psi ψ 为基本小波函数。由于是离散变换， a = 2 j , j ∈ Z a=2^j, j \in \mathbb{Z} a=2j,j∈Z 且 b = 2 j l , l ∈ Z b=2^j l, l \in \mathbb{Z} b=2jl,l∈Z，因此公式（5）可表示为：

ψ a , b ( t ) = 1 a ∑ n ψ ( t − b a ) = 2 − j / 2 ∑ n ψ ( 2 − j t − l ) (6) \psi_{a,b}(t) = \frac{1}{\sqrt{a}} \sum_{n} \psi\left(\frac{t-b}{a}\right) = 2^{-j/2} \sum_{n} \psi\left(2^{-j} t - l\right) \tag{6} ψa,b(t)=a 1n∑ψ(at−b)=2−j/2n∑ψ(2−jt−l)(6)

其中，尺度 a a a 通过尺度因子 j j j 重新定义，且随着 j j j 增大，尺度变得更粗糙。

理论上，希尔伯特空间中的基本小波函数 ψ \psi ψ 可分为两部分：对应原始函数低频部分的尺度函数 φ ( ⋅ ) \varphi(\cdot) φ(⋅)，以及对应高频部分的小波函数 ψ ( ⋅ ) \psi(\cdot) ψ(⋅)。因此，由水平（ u 1 u_1 u1）和垂直（ u 2 u_2 u2）方向离散小波变换输出构成的二维离散小波变换（2D DWT）包含一个尺度函数 φ ( ⋅ ) \varphi(\cdot) φ(⋅) 和三个小波函数 ψ ( ⋅ ) \psi(\cdot) ψ(⋅)：

{ φ ( u ) = φ ( u 1 ) φ ( u 2 ) ψ h ( u ) = φ ( u 1 ) ψ ( u 2 ) ψ v ( u ) = ψ ( u 1 ) φ ( u 2 ) ψ d ( u ) = ψ ( u 1 ) ψ ( u 2 ) (7) \begin{cases} \varphi(u) = \varphi(u_1) \varphi(u_2) \\ \psi^h(u) = \varphi(u_1) \psi(u_2) \\ \psi^v(u) = \psi(u_1) \varphi(u_2) \\ \psi^d(u) = \psi(u_1) \psi(u_2) \end{cases} \tag{7} ⎩ ⎨ ⎧φ(u)=φ(u1)φ(u2)ψh(u)=φ(u1)ψ(u2)ψv(u)=ψ(u1)φ(u2)ψd(u)=ψ(u1)ψ(u2)(7)

其中， u u u 为二维输入， h , v , d h, v, d h,v,d 分别表示对水平、垂直和对角边缘的敏感性； φ ( ⋅ ) \varphi(\cdot) φ(⋅) 和 ψ ( ⋅ ) \psi(\cdot) ψ(⋅) 分别代表低通滤波器和高通滤波器，用于图像近似和边缘特征提取。

根据公式（7），我们使用二维离散小波变换处理图像，如公式（8）和图5所示。

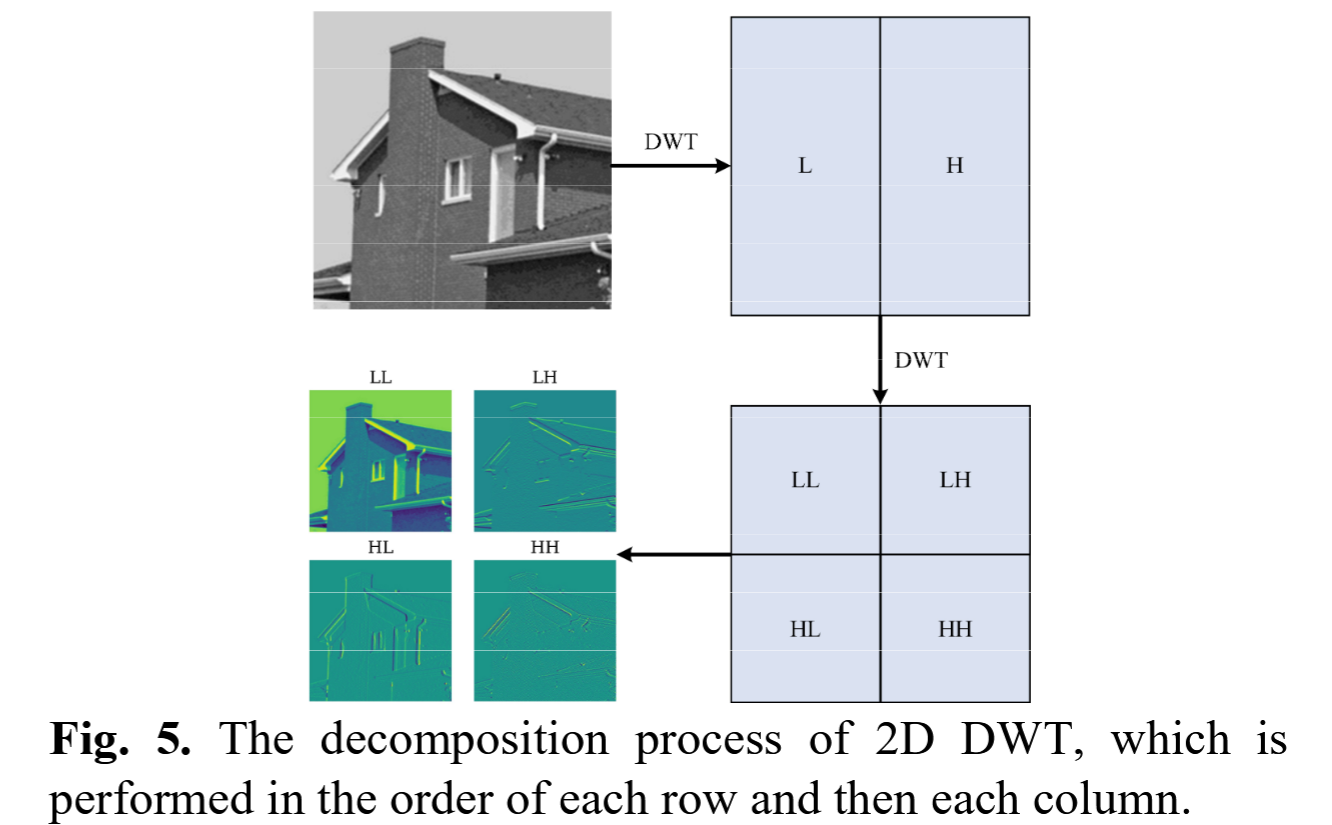
图5. 二维离散小波变换的分解过程，该过程按先对每行执行（离散小波变换）、再对每列执行（离散小波变换）的顺序进行。

首先，对图像的每一行执行离散小波变换，得到水平方向的低频分量 L L L 和高频分量 H H H；然后，对变换后数据的每一列执行离散小波变换，得到水平和垂直方向均为低频的分量 L L LL LL、水平低频且垂直高频的分量 L H LH LH、水平高频且垂直低频的分量 H L HL HL，以及水平和垂直方向均为高频的分量 H H HH HH。

{ L L , L H , H L , H H } = 2 D DWT ( X ) , { L L = φ ( X ) = φ ( x 1 ) φ ( x 2 ) L H = ψ L H ( X ) = φ ( x 1 ) ψ ( x 2 ) H L = ψ H L ( X ) = ψ ( x 1 ) φ ( x 2 ) H H = ψ H H ( X ) = ψ ( x 1 ) ψ ( x 2 ) (8) \begin{aligned} & \{LL, LH, HL, HH\} = 2\text{D DWT}(X), \\ & \begin{cases} LL = \varphi(X) = \varphi(x_1) \varphi(x_2) \\ LH = \psi^{LH}(X) = \varphi(x_1) \psi(x_2) \\ HL = \psi^{HL}(X) = \psi(x_1) \varphi(x_2) \\ HH = \psi^{HH}(X) = \psi(x_1) \psi(x_2) \end{cases} \end{aligned} \tag{8} {LL,LH,HL,HH}=2D DWT(X),⎩ ⎨ ⎧LL=φ(X)=φ(x1)φ(x2)LH=ψLH(X)=φ(x1)ψ(x2)HL=ψHL(X)=ψ(x1)φ(x2)HH=ψHH(X)=ψ(x1)ψ(x2)(8)

其中，输入 X ∈ R C × H × W X \in \mathbb{R}^{C \times H \times W} X∈RC×H×W 被分解为四个离散小波子带（ L L , L H , H L , H H ∈ R C × H / 2 × W / 2 LL, LH, HL, HH \in \mathbb{R}^{C \times H/2 \times W/2} LL,LH,HL,HH∈RC×H/2×W/2）； x 1 x_1 x1 和 x 2 x_2 x2 分别代表水平和垂直方向。

显然， L L LL LL 主要保留有助于目标识别的主要结构信息，而 L H LH LH、 H L HL HL 和 H H HH HH 分别表示水平、垂直和对角方向的细节信息。WaveCNet[46]仅利用低频分量，丢弃了所有含丰富细节信息的高频分量。FWFC[48]认为，图像域中的细微差异可在特定小波波段中被突出，这有助于识别小目标。因此，我们选择进一步利用高频信息调制低频分量。首先，将 L H LH LH 和 H L HL HL 进行逐元素相加，然后生成高频权重 W high W_{\text{high}} Whigh：

W high = δ ( L H + H L ) , ∈ R C × H / 2 × W / 2 (9) W_{\text{high}} = \delta(LH + HL), \in \mathbb{R}^{C \times H/2 \times W/2} \tag{9} Whigh=δ(LH+HL),∈RC×H/2×W/2(9)

其中， δ \delta δ 为softmax函数，用于归一化全局细节特征。

随后，将 W high W_{\text{high}} Whigh 与低频分量 L L LL LL 进行哈达玛积运算（逐个元素相乘），得到注意力矩阵 A t t Att Att。不断调整 A t t Att Att 的过程等价于在选择与不选择之间进行权衡。

A t t = W high ⊙ L L , ∈ R C × H / 2 × W / 2 (10) Att = W_{\text{high}} \odot LL, \in \mathbb{R}^{C \times H/2 \times W/2} \tag{10} Att=Whigh⊙LL,∈RC×H/2×W/2(10)

通过将输入特征 X X X 与注意力矩阵进行逐元素相加，我们得到加权特征 Y Y Y：

Y = A t t + L L , ∈ R C × H / 2 × W / 2 (11) Y = Att + LL, \in \mathbb{R}^{C \times H/2 \times W/2} \tag{11} Y=Att+LL,∈RC×H/2×W/2(11)

小波池化层将输入信号分解为四个离散小波子带，无信息丢失，并将细节信息嵌入输出中。因此，小波池化层确保池化后的输入特征 X X X 能够被充分保留和恢复，同时保证小目标不受混叠效应和噪声的影响。

五、图增强模块GEM

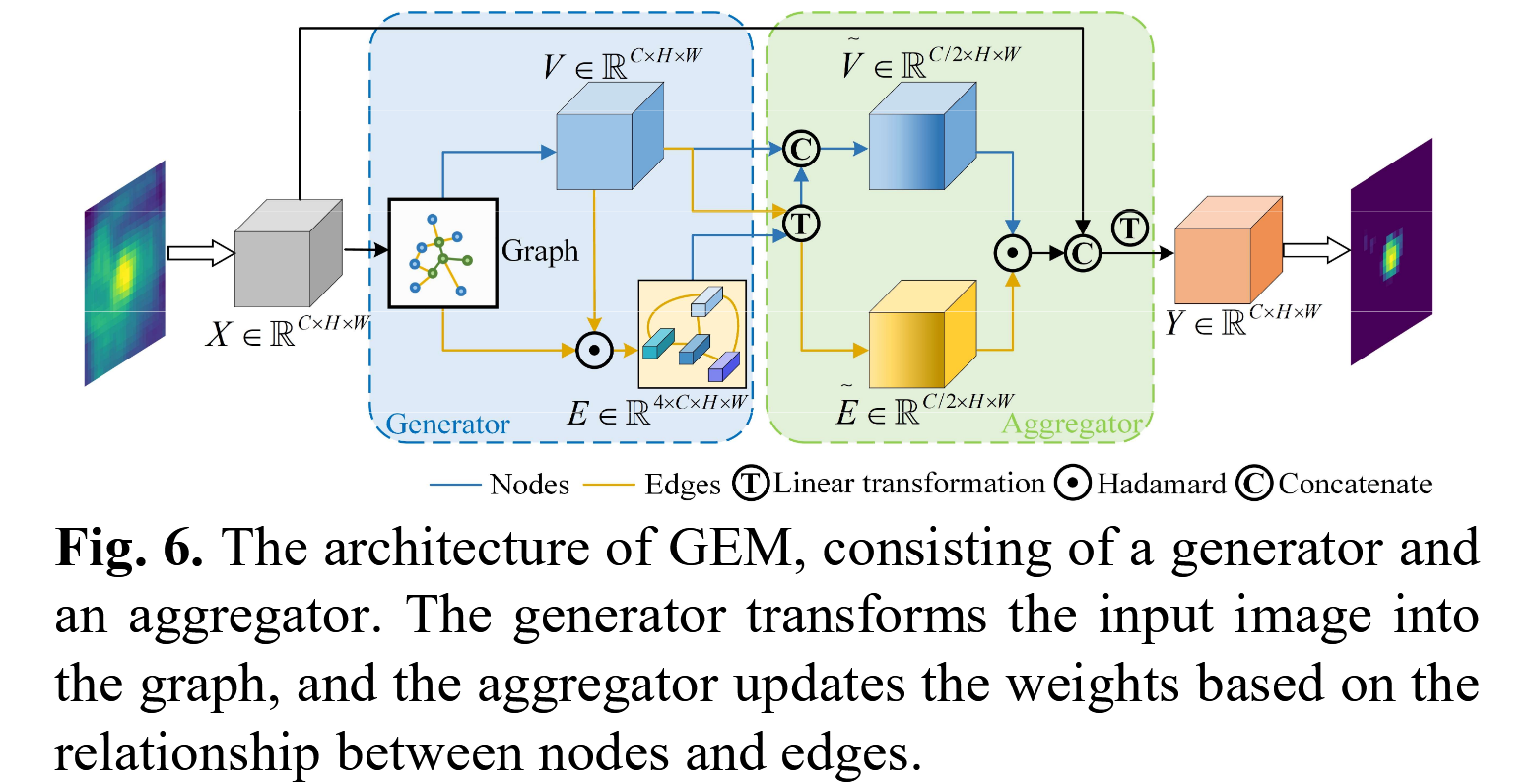
图6. 图增强模块（GEM）的架构，由生成器和聚合器组成。生成器将输入图像转换为图，聚合器则基于节点和边之间的关系更新权重。

  1. 生成器构建图表示 ：GEM着重考量分类响应中物体间的潜在关系，以此增强小目标的响应，避免其被背景噪声淹没。GEM能够为像素关系生成有效的图表示，这对小目标跟踪极为有利。GEM由生成器和整合器构成。首先，生成器将输入 X X X表示为包含节点和边的图，数学表达式为： G ( V , E ) = f ( X ) G(V, E) = f(X) G(V,E)=f(X) 其中 X ∈ R C × H × W X \in \mathbb{R}^{C\times H\times W} X∈RC×H×W为输入， V ∈ R C × H × W V \in \mathbb{R}^{C\times H\times W} V∈RC×H×W是节点集合， E ∈ R 4 × C × H × W E \in \mathbb{R}^{4\times C\times H\times W} E∈R4×C×H×W是边， f f f表示生成器。将输入 X X X视作节点，并基于节点生成边，这里边的组成仅考虑节点和其四个最近的节点。因此，可进一步表示为： E i , j = { V i ′ , j ′ ∣ ( i ′ , j ′ ) ∈ N ( i , j ) } E_{i,j} = \left\{V_{i',j'}\mid (i',j') \in \mathcal{N}(i,j)\right\} Ei,j={Vi′,j′∣(i′,j′)∈N(i,j)} 其中 N ( i , j ) \mathcal{N}(i,j) N(i,j)代表节点 ( i , j ) (i,j) (i,j)的四个最近邻节点集合 。

  2. 整合器更新节点关系 ：基于得到的 G ( V , E ) G(V, E) G(V,E)，整合器梳理并更新节点 V V V和边 E E E之间的关系。然后，依据节点之间的关系（即 E E E）更新节点 V V V，且与感兴趣区域（即目标区域）相关的节点的激活值越高，其更新公式为： V i , j ′ = ∑ ( i ′ , j ′ ) ∈ N ( i , j ) ω ( i , j ) , ( i ′ , j ′ ) V i ′ , j ′ V'{i,j} = \sum{(i',j')\in \mathcal{N}(i,j)} \omega_{(i,j),(i',j')} V_{i',j'} Vi,j′=(i′,j′)∈N(i,j)∑ω(i,j),(i′,j′)Vi′,j′ 其中 ω ( i , j ) , ( i ′ , j ′ ) \omega_{(i,j),(i',j')} ω(i,j),(i′,j′)是根据边 E E E计算得到的权重系数 ，反映了节点 ( i , j ) (i,j) (i,j)与相邻节点 ( i ′ , j ′ ) (i',j') (i′,j′)之间的关联强度。

  3. 更新边的权重 ：接下来，为更新边 E E E的权重，GEM会重复堆叠节点，然后使用全连接层进行线性变换，以完成边的更新，具体表示为： E ′ = σ ( F C ( Stack ( V ) ) ) E' = \sigma\left(FC\left(\text{Stack}(V)\right)\right) E′=σ(FC(Stack(V))) 其中 Stack ( V ) \text{Stack}(V) Stack(V)表示对节点 V V V进行堆叠操作， F C FC FC代表全连接层运算， σ \sigma σ为激活函数（如ReLU等），通过该过程得到更新后的边权重 E ′ E' E′ 。

  4. 融合更新特征并调节输入 ：最后，融合更新的节点和边特征，以调节输入 X X X，从而实现权重的重新分配，使目标区域的激活值较高，背景区域的激活值较低，其运算如下： X ′ = α V ′ + ( 1 − α ) E ′ X' = \alpha V' + (1 - \alpha) E' X′=αV′+(1−α)E′ 其中 α \alpha α是用于平衡节点特征 V ′ V' V′和边特征 E ′ E' E′融合比例的超参数 。

基于图理论，GEM具备强大的知识表示和结构特征，对分类响应的像素级调制能够有效提升对小目标的分辨能力。

六、实验

热门推荐
01Cursor Claude 模型无法使用的解决方法02全球最强模型Grok4，国内已可免费使用！（附教程）03KGG转MP3工具|非KGM文件|解密音频04Cursor如何配置代理05【无标题】06集群聊天服务器---MySQL数据库的建立07突破限制：使用 Claude Code Proxy 让 Claude Code 自由连接任意模型08绿色建筑新态势：楼宇自控助力能效提升，推动成本优化新路径09Coze扣子平台完整体验和实践（附国内和国际版对比）10（5千字总结）国内如何安装和使用 Claude Code 的保姆级教程 - 支持Mac和Windows用户