文章目录
最小栈
题目描述

解题思路
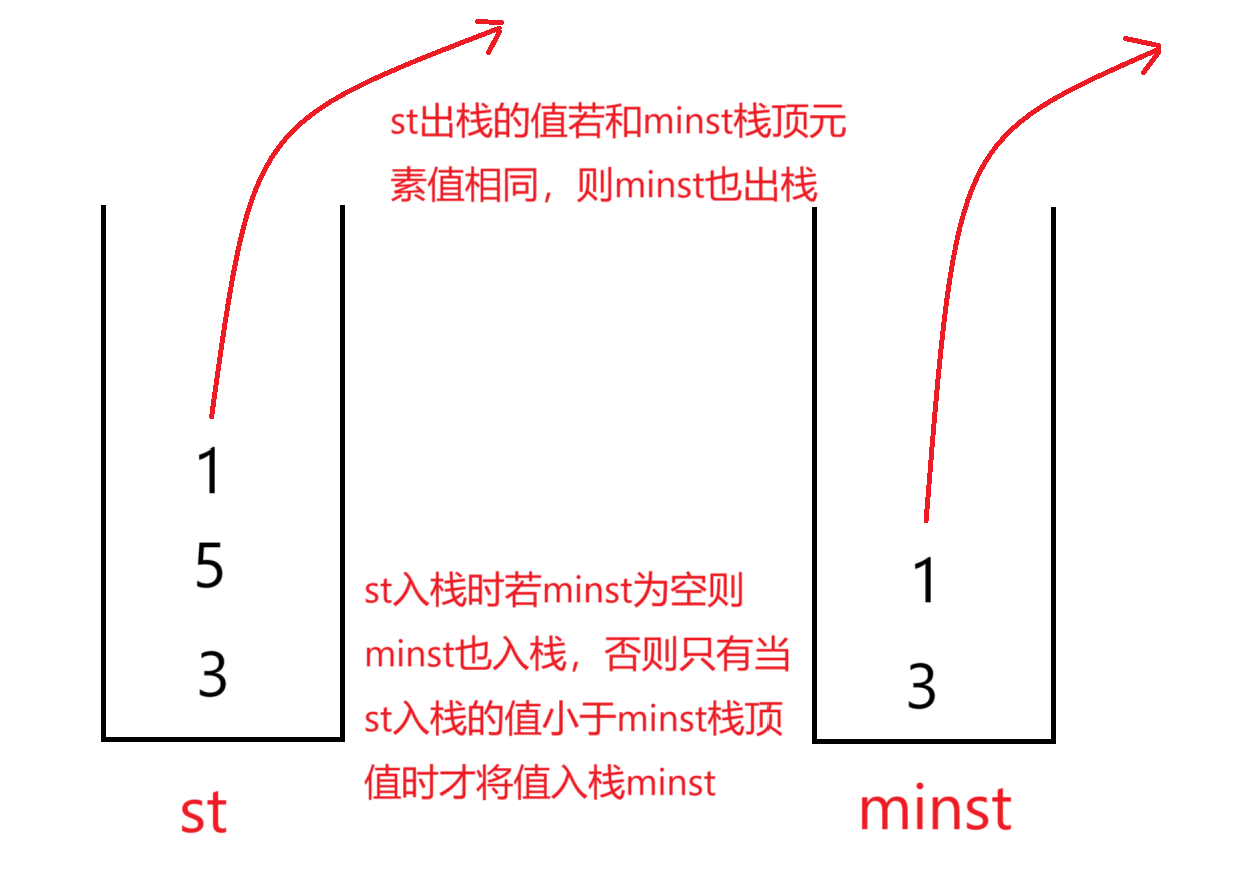
这道题如果只用一个栈效率很低,因为无法记录栈中除最小元素以外的第二小第三小...元素,如果把栈中最小元素pop掉之后,需要循环遍历栈中所有元素找到剩余元素中最小的元素。
最好的方法是除了普通栈外,再创建一个最小栈,用来记录栈中每一个阶段的最小元素(把栈每插入或删除一个元素后的状态视为一个阶段),详细解释见下图:
代码
cpp
class MinStack {
public:
MinStack()
{}
void push(int val) {
_st.push(val);
if(empty(_stmin) || val <= _stmin.top())
{
_stmin.push(val);
}
}
void pop() {
assert(!_st.empty());
if(_st.top() == _stmin.top())
_stmin.pop();
_st.pop();
}
int top() {
return _st.top();
}
int getMin() {
return _stmin.top();
}
private:
stack<int> _st;
stack<int> _stmin;
};栈的压入弹出序列
题目描述
解题思路
这道题要用到模拟思想,也就是模拟数据入栈和出栈的过程,这里要用到一个栈来模拟,两个下标pushi、popi分别指向pushV和popV的第一个数据,首先一个for循环依次将pushV的数据入栈,每入栈一个数据都要和popV的数据比较,若不相等则继续入栈,若相等就将栈pop一次并且popi++,然后继续比较栈顶数据与popV的数据,若相等继续执行:将栈pop一次并且popi++,直到栈为空或者栈顶数据与popV的数据不相等退出循环(这里一定要先判断栈是否为空,否则可能越界访问),退出循环后继续执行外层for循环直到遍历完pushV的数据,若出for循环后栈为空,则说明模拟成功返回true,若栈不为空则模拟失败返回false。
代码
cpp
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pushV int整型vector
* @param popV int整型vector
* @return bool布尔型
*/
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
stack<int> st;
int pushi = 0;
int popi = 0;
for(pushi = 0; pushi < pushV.size(); pushi++)
{
//入栈序列入栈
st.push(pushV[pushi]);
//栈顶尝试与出栈序列匹配
while (!st.empty() && st.top() == popV[popi])
{
st.pop();
popi++;
}
}
return st.empty();
}
};逆波兰表达式求值
题目描述
首先来认识一下什么是逆波兰表达式:

它的特点是运算符按优先级排列,且挨着要运算的运算数,它没有括号,严格遵循从左到右计算,非常适合计算机读取计算。
解题思路
这道题用栈非常契合逆波兰表达式的特点,首先我们要遍历整个数组,当遇到数字时会将它入栈,当遍历到操作符时只要取栈顶的两个数字就取到操作符对应的两个操作数了,因为操作符是紧挨着它的操作数的,计算完表达式结果后再将结果入栈,该表达式结果又会作为下一次计算表达式的操作数,最后栈剩余的一个数据就是表达式的结果。
这里要注意,题目是以vector< string>的形式给的参数,所以用范围for遍历最方便,判断范围for取到的值是操作符还是整型数字,是操作符就直接入栈,是操作数就取栈顶两个数据计算表达式再把表达式结果入栈,注意两个操作数的顺序。
因为迭代器取到的数据是字符串,所以还要把整型字符串转换成整型数字,需要用到string的全局函数stoi。
代码
cpp
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for(auto e : tokens)
{
if(e == "+" || e == "-" ||e == "*" ||e == "/")
{
int b = st.top();
st.pop();
int a = st.top();
st.pop();
int c = 0;
switch(e[0])
{
case '+':
st.push(a + b);
break;
case '-':
st.push(a - b);
break;
case '*':
st.push(a * b);
break;
case '/':
st.push(a / b);
break;
default:
break;
}
}
else
{
st.push(stoi(e));
}
}
return st.top();
}
};二叉树的层序遍历
题目描述
解题思路
这道题我们首先要理解二叉树的层序遍历,小编已经整理过相关资料啦:详情点这里
这道题就是普通层序遍历的pro max版,首先它需要按层打印,把每一层的结果放到一个vector,最后把所有层数组合并为一个二维数组并打印,这一点因为我们有vector很好实现,主要是如何把每一层提取到一起放在同一个vector,因为队列中会存在不同层是数据,这里小编提供两个思路:
1、和最小栈类似,再创建一个用来存放每一个结点层数数据的queue<int>,它和普通栈执行一样的操作。
2、这道题的主要矛盾是无法识别队列中结点属于那一层,我们可以借助层序遍历的特点:它会逐层遍历,当把一层遍历完后再开始遍历下一层。
我们可以设置一个变量levelsize用来记录每一层的结点个数,首先当存在根节点时把levelsize置为1,当根出队列时会把它的孩子结点带入队列,这是队列中的结点个数就是下一层的levelsize,依此类推,当出完一层的结点后,队列中结点个数就是下一层的levelsize,当遍历同一层结点时,每遍历完一个结点就levelsize--,直到levelsize为0代表该层结点遍历完毕,开始遍历下一层。
第二个思路更简便,我们下面就第二个思路来完成代码。
代码
cpp
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> q;
int levelsize = 0;
if(root)
{
q.push(root);
levelsize = 1;
}
vector<vector<int>> vv;
while(!q.empty())
{
//把二叉树一层结点的数据写入一维vector v
vector<int> v;
while(levelsize--)
{
TreeNode* front = q.front();
v.push_back(front->val);
q.pop();
if(front -> left)
q.push(front -> left);
if(front -> right)
q.push(front -> right);
}
vv.push_back(v);
//一层结点出完后,队列中剩余结点个数就是下一层的结点个数
levelsize = q.size();
}
return vv;
}
};以上就是小编分享的全部内容了,如果觉得不错还请留下免费的赞和收藏
如果有建议欢迎通过评论区或私信留言,感谢您的大力支持。
一键三连好运连连哦~~
