2025测绘程序设计国赛实战：一轮终章 | 单向后方交会C#实现

前言

本文是小编对六道国赛试题中的最后一个试题，单向后方交会的一篇学习日志。

本文的整体架构，依旧首先拿训练数据跟大家介绍本题涉及到的数据的属性含义，涉及到算法的原理、执行流程和终极目的。然后附上小编用C#来实现的程序，从窗体设计到各大类体。最后的总结部分，会跟大家分享小编的一些思考，然后这也是小编的废话文学区哈哈。

小编的任务，就是20号之前完成六道赛题的第一轮摸排。过去的日子里，从六月中旬开始吧，就一点一点研究这六个题目，从RANSAC开始，到GNSS，地图图幅，再到GNSS基于7月最新资讯的更新，泰森，后方，为国赛搭建起的专栏中的文章从0到9，这也是一种时间的可视化吧哈哈。

小编没有出关于点云去噪的文章，因为这个考到的概率，emmm，不多说了大家应该懂哈哈，不过可能之后我还是会捏一篇简单的关于这道题的思路和实现方案的分享，之后再看。

一、数据＆原理解析

（一）数据

上半部分:(相机内方位元素，考到一定会给的，知道是干嘛的就行)
- fk(mm) ：相机主距，单位为毫米（mm）。
  
  含义：相机镜头中心到像平面（感光元件）的距离，是相机的核心内方位元素（就相当于一个来确定放缩系数的参数吧）。
  
  作用：共线方程中需用主距计算像点与摄影中心的几何关系，直接影响像点坐标的投影精度。
- x0、y0 ：像主点坐标，单位为毫米（mm）。
  
  含义：相机主光轴与像平面的交点坐标，理想情况下位于像平面中心（此处均为 0）。
  
  作用：共线方程中需用像主点坐标校正像点位置，消除镜头光学中心与像平面中心不重合的误差（简单讲，就是起一个原点的作用）。
- m ：摄影比例尺分母。
  
  作用：用于估计摄影中心初始 Z 坐标（Zs0 = m × fk），为迭代计算提供合理初值，加速收敛。
下半部分（控制点）:
- x(mm)、y(mm) ：像点坐标，单位为毫米（mm）。
  
  含义：控制点在影像上的投影位置坐标，就是所谓像点坐标。
  
  作用：作为共线方程的观测值，与物方坐标联立求解外方位元素。
- X(m)、Y(m)、Z(m) ：物方坐标，单位为米（m）。
  
  含义：控制点在地面坐标系中的实际三维坐标，真值。
  
  作用：作为已知基准，在共线方程中拿来解算外方位元素。
为啥用这些？
- 相机内方位元素**（fk、x0、y0）**：就是一把尺，用这个尺子，来建立起像点和物方点的关系。（就是建立起成像与真实的关系）
- 比例尺（m）：用来估计摄影重心高度Z滴，是为算法服务的。
- 控制点（x、y与X、Y、Z）：像点坐标（x、y）是观测值，反映物方点在影像上的投影位置；物方坐标（X、Y、Z）是已知真值，用于约束外方位元素的解算。两者结合形成 "观测 - 已知" 对，通过共线方程反推相机的位置和姿态（就是外方位元素）。

（二）核心实现方案

单像空间后方交会的核心目标就是通过控制点求解共线方程中的外方位元素，从而建立物方坐标与像点坐标之间的数学关系，还是一个对参数的最优估计问题。（这部分用到的各种公式的详细介绍，小编总结之后，放在与本篇绑定的PDF中了，大家可参考着看）

旋转矩阵（`a1~c3`的计算）

What: 旋转矩阵R是三个基本矩阵的乘积：R = R_Z(κ) · R_Y(ω) · R_X(φ)
**Why:**描述像空间坐标系到物方空间坐标系的旋转关系，是求解像点坐标的基础。(基本矩阵见下图，不过只需要理解这玩意儿在干嘛就OK，公式不必太深究)

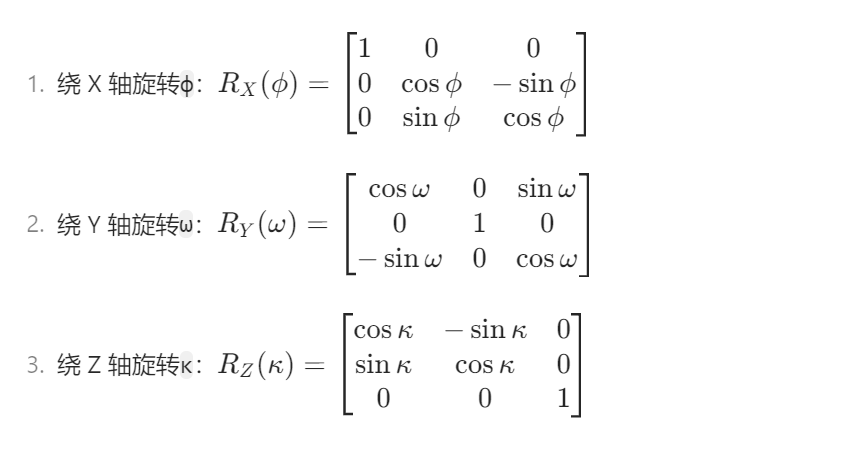
cs 复制代码

a1 = Cos(phi) * Cos(kapa) - Sin(phi) * Sin(omiga) * Sin(kapa);  // R[0,0]
a2 = -Cos(phi) * Sin(kapa) - Sin(phi) * Sin(omiga) * Cos(kapa); // R[0,1]
a3 = -Sin(phi) * Cos(omiga);                                   // R[0,2]
b1 = Cos(omiga) * Sin(kapa);                                   // R[1,0]
b2 = Cos(omiga) * Cos(kapa);                                   // R[1,1]
b3 = -Sin(omiga);                                              // R[1,2]
c1 = Sin(phi) * Cos(kapa) + Cos(phi) * Sin(omiga) * Sin(kapa);  // R[2,0]
c2 = -Sin(phi) * Sin(kapa) + Cos(phi) * Sin(omiga) * Cos(kapa); // R[2,1]
c3 = Cos(phi) * Cos(omiga);                                    // R[2,2]

像点近似坐标计算

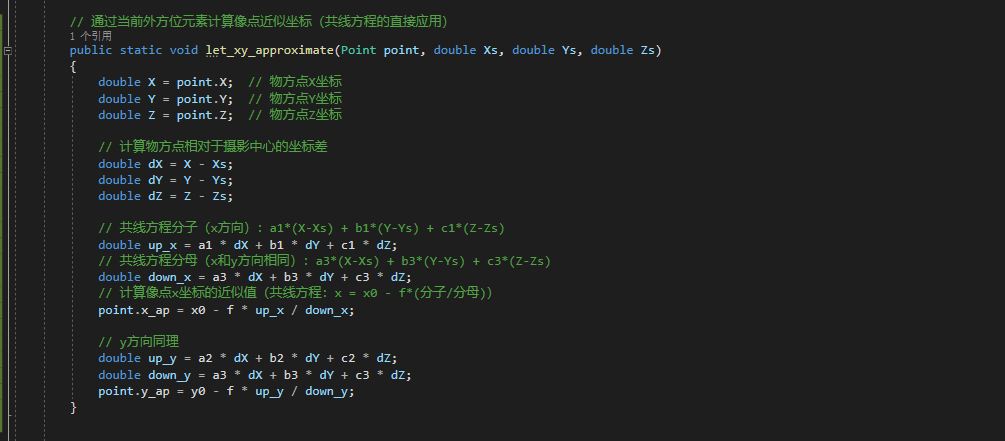
What: 通过设置的外方位元素计算像点的近似坐标(x_ap, y_ap)，对应共线方程的直接应用。
Why:x_ap, y_ap是用当前外方位元素（近似值）计算的像点 "理论坐标"，后续会与观测值(x,y)对比，计算误差用于迭代优化。

cs 复制代码

// 计算物方点到摄影中心的偏移量
double dX = X - Xs;  // X - Xs
double dY = Y - Ys;  // Y - Ys
double dZ = Z - Zs;  // Z - Zs

// 共线方程分子（x方向）：a1*(X-Xs) + b1*(Y-Ys) + c1*(Z-Zs)
double up_x = a1 * dX + b1 * dY + c1 * dZ;
// 共线方程分母（x和y方向相同）：a3*(X-Xs) + b3*(Y-Ys) + c3*(Z-Zs)
double down_x = a3 * dX + b3 * dY + c3 * dZ;
// 近似x坐标：x0 - f*(分子/分母)（对应共线方程x的表达式）
point.x_ap = x0 - f * up_x / down_x;

// y方向同理
double up_y = a2 * dX + b2 * dY + c2 * dZ;
double down_y = a3 * dX + b3 * dY + c3 * dZ;
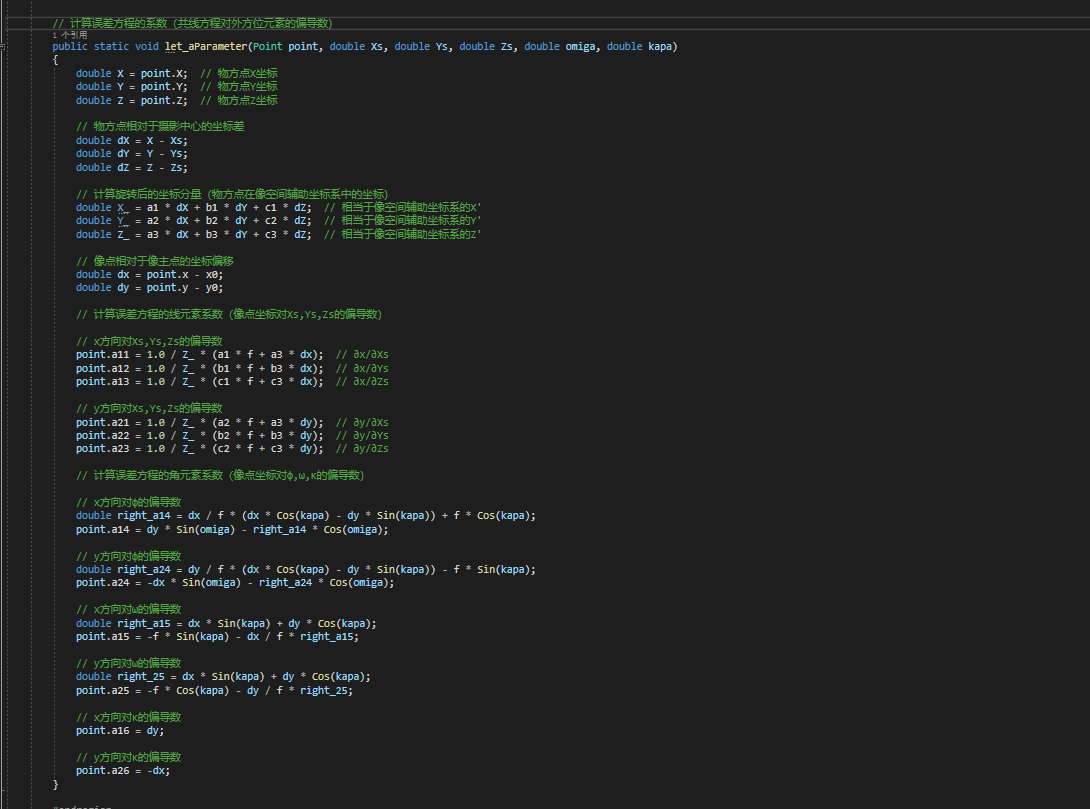
point.y_ap = y0 - f * up_y / down_y;

误差方程系数

What: 是共线方程对外方位元素的偏导数 （变化率）(外方位元素有6个，每一个像点(x,y)对应 2 个偏导方程，6×2，要产生12个系数)
Why:把非线性的共线方程转化为线性的误差方程，咱们之后就是要用最小二乘来基于误差方程进行求最优解滴。

cs 复制代码

// N = a1*dX + b1*dY + c1*dZ（共线方程分子）
double X_ = a1 * dX + b1 * dY + c1 * dZ;  
// D = a3*dX + b3*dY + c3*dZ（共线方程分母）
double Z_ = a3 * dX + b3 * dY + c3 * dZ;  
// (x - x0)：像点观测值与像主点的偏移
double dx = point.x - x0;  
double dy = point.y - y0;  

// a11 = x对Xs的偏导数：(a1*f + a3*dx)/Z_
point.a11 = 1.0 / Z_ * (a1 * f + a3 * dx);  
// a12 = x对Ys的偏导数：(b1*f + b3*dx)/Z_
point.a12 = 1.0 / Z_ * (b1 * f + b3 * dx);  
// a13 = x对Zs的偏导数：(c1*f + c3*dx)/Z_
point.a13 = 1.0 / Z_ * (c1 * f + c3 * dx);  

// y方向同理（a21~a23是y对Xs,Ys,Zs的偏导数）
point.a21 = 1.0 / Z_ * (a2 * f + a3 * dy);  
point.a22 = 1.0 / Z_ * (b2 * f + b3 * dy);  
point.a23 = 1.0 / Z_ * (c2 * f + c3 * dy);

最小二乘法与矩阵运算（法方程求解）

What: 单像空间后方交会本质是 "解超定方程组"（说人话，就是方程数量多于未知数数量的方程组），咱需用最小二乘法求最优解。（又是矩阵哈哈）
**Why:**通过矩阵运算，得到外方位元素的改正数(要拿去校准现有值的尺子)，用于迭代优化。

cs 复制代码

// 1. 计算A的转置矩阵A^T
var AT = Transpose(A);  

// 2. 计算A^T·A（法方程左边矩阵）
var ATA = Multiply(AT, A);  

// 3. 计算A^T·A的逆矩阵(A^T·A)⁻¹
var ATA_inverse = Inverse(ATA);  

// 4. 计算A^T·L（法方程右边向量）
var ATL = Multiply(AT, L);  

// 5. 求解改正数ΔX = (A^T·A)⁻¹ · (A^T·L)
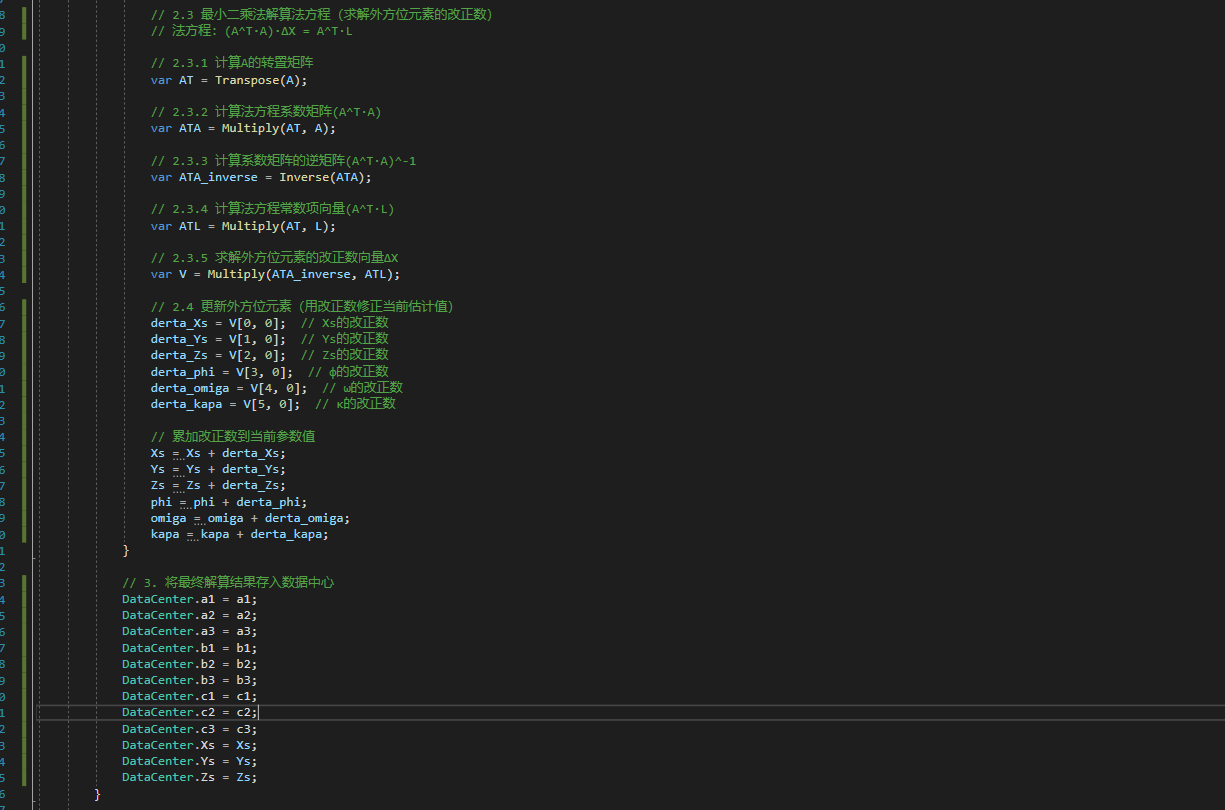
var V = Multiply(ATA_inverse, ATL);

迭代更新（外方位元素的优化）

What:每次迭代后用改正数更新外方位元素，直到改正数足够小,就是无限接近真值（也就是所谓收敛）。

cs 复制代码

// 用改正数更新外方位元素
derta_Xs = V[0, 0];  // ΔXs
derta_Ys = V[1, 0];  // ΔYs
// ... 其他改正数
Xs = Xs + derta_Xs;  // Xs_new = Xs_old + ΔXs
Ys = Ys + derta_Ys;  // Ys_new = Ys_old + ΔYs
// ... 其他元素同理

（三）小总结

//这道题的整体实现思路：

基操：
- 窗体
- 数据结构
- 数据读取＆管理
算法：
- 一般来讲，把各个步骤放到各个方法中具体实现，然后定义一个main方法作为处理入口，在这一方法中对整体算法进行调用，这样会好看一点。以下是处理步骤：
  - 用旋转矩阵描述相机姿态；
  - 用共线方程计算像点近似坐标；
  - 用偏导数构建误差方程的系数矩阵；
  - 用法方程求解外方位元素的改正数；
  - 迭代更新外方位元素，直到收敛。

二、C#实现

（一）窗体

//一以贯之的风格，说到做到的小编哈哈哈哈。

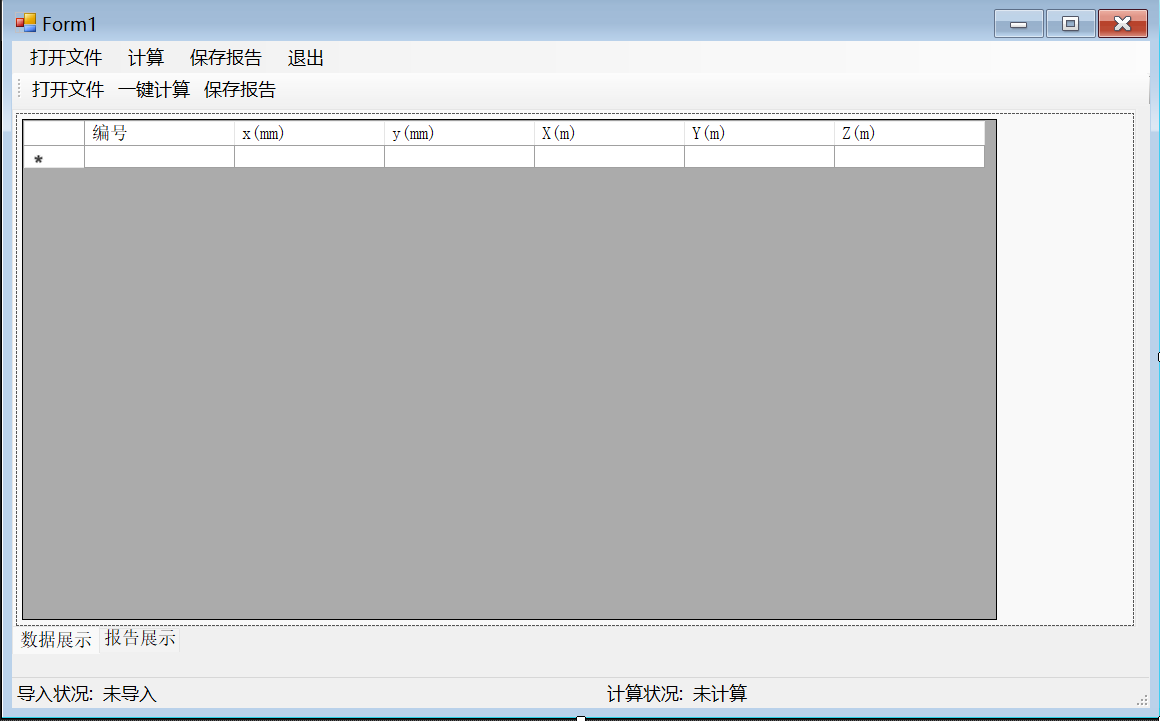
（二）核心算法类

Main

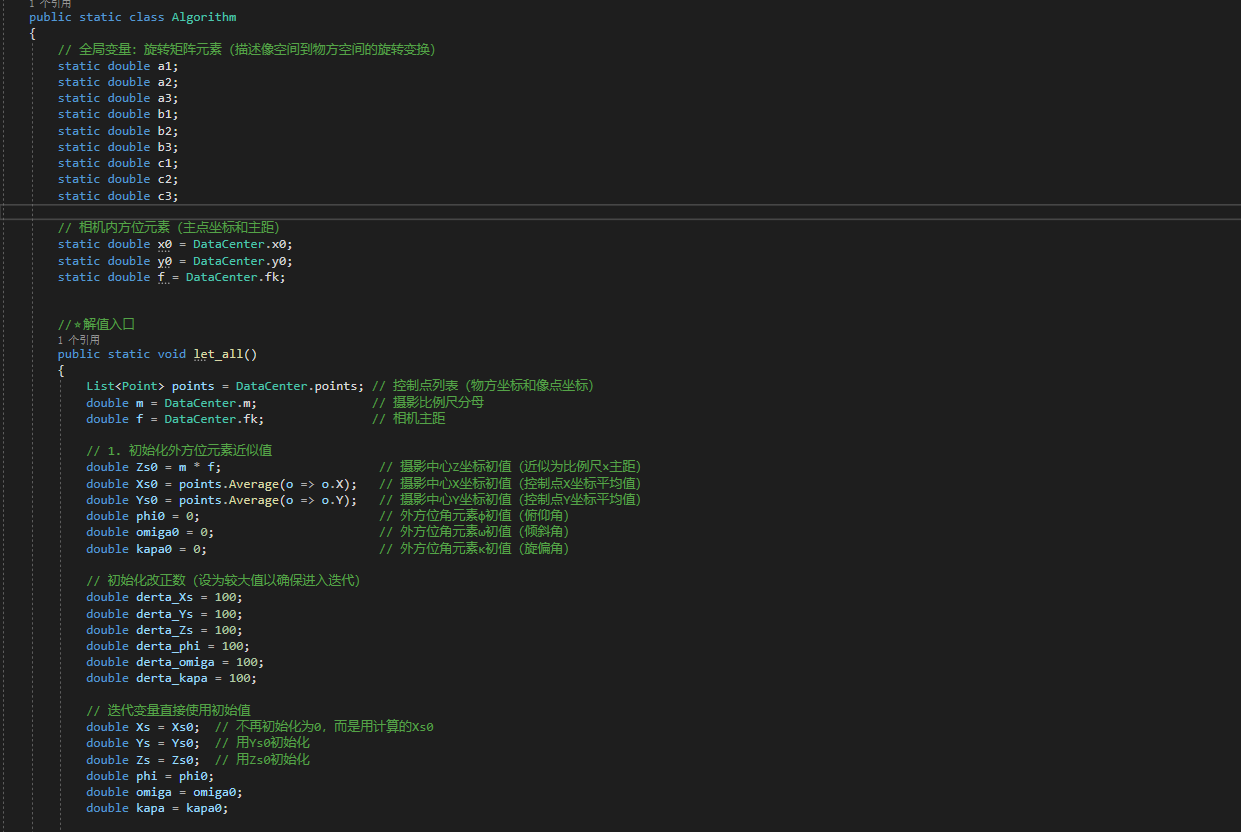
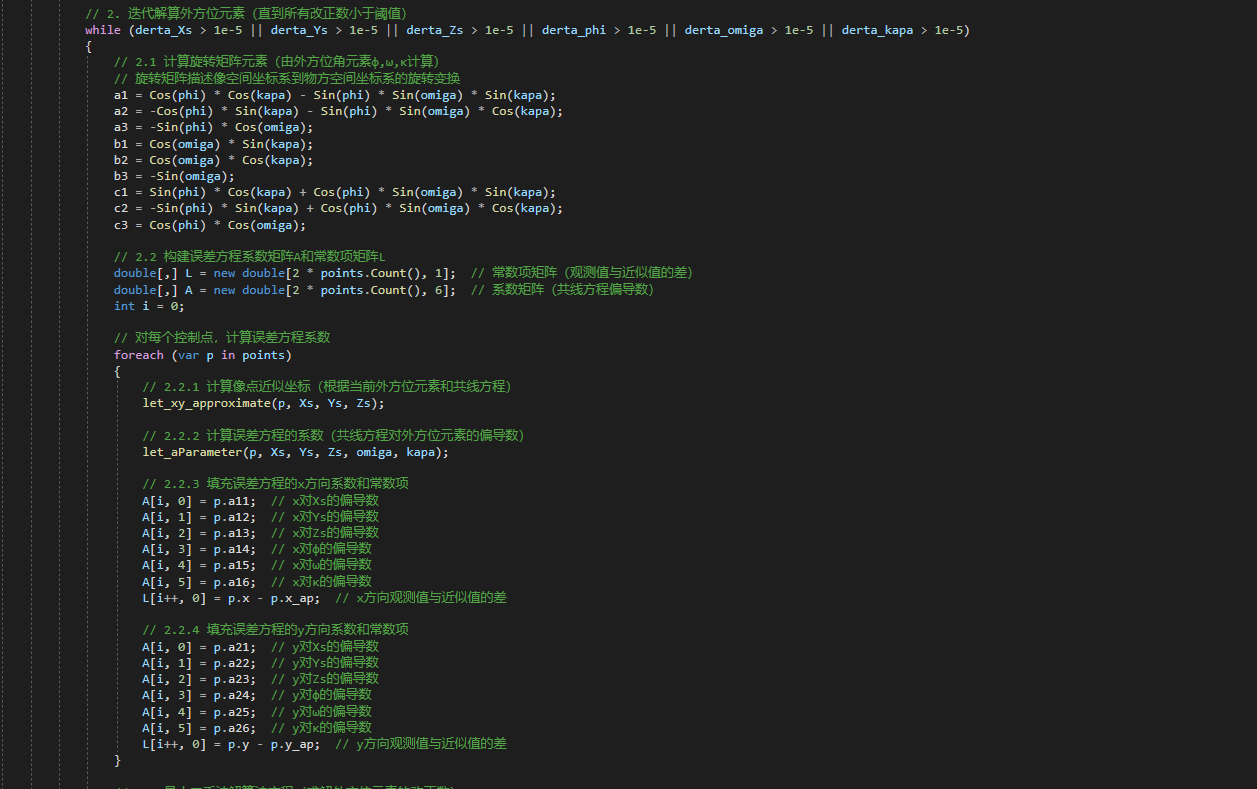
参数辅助

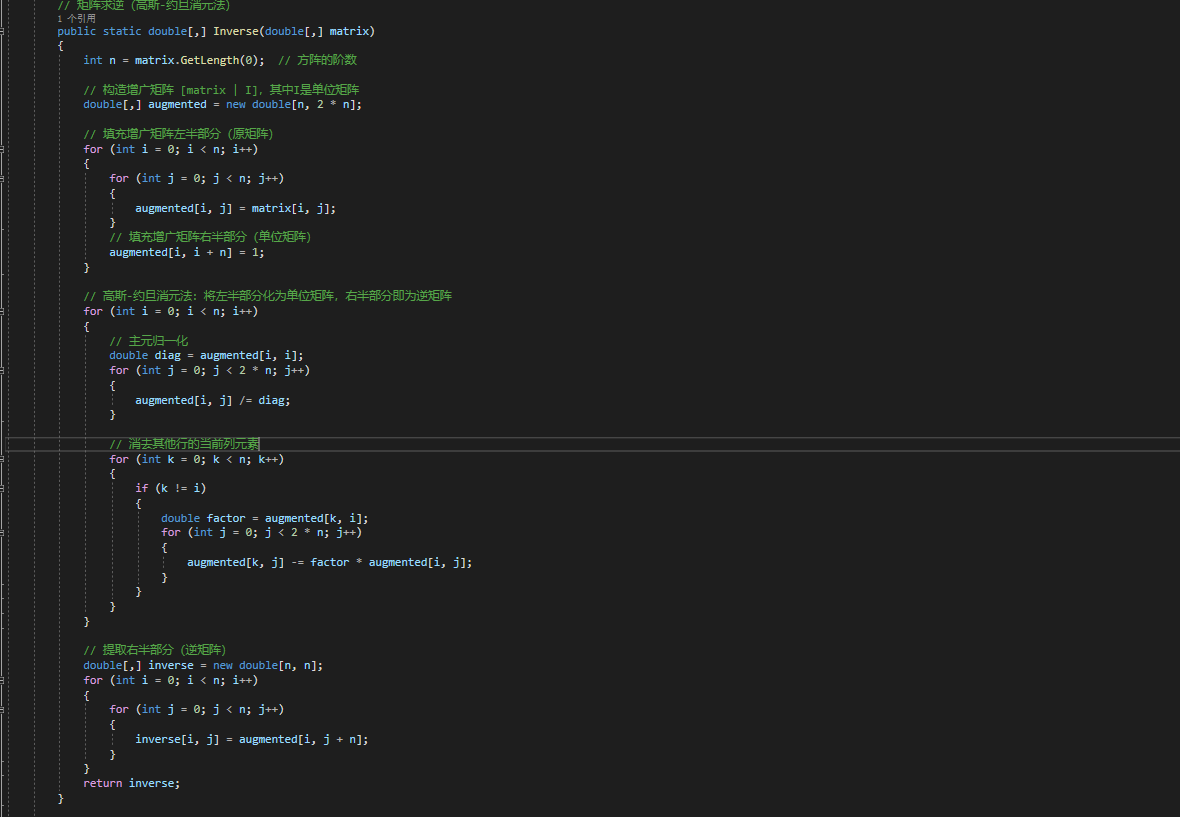
矩阵

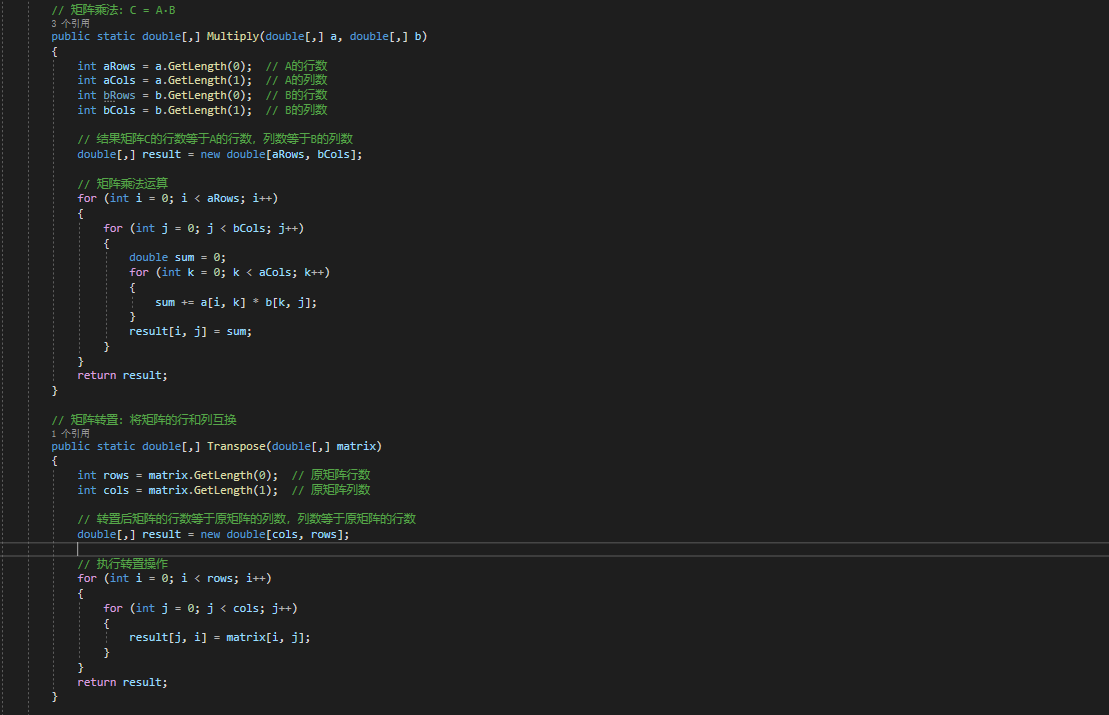
（三）各大辅助类

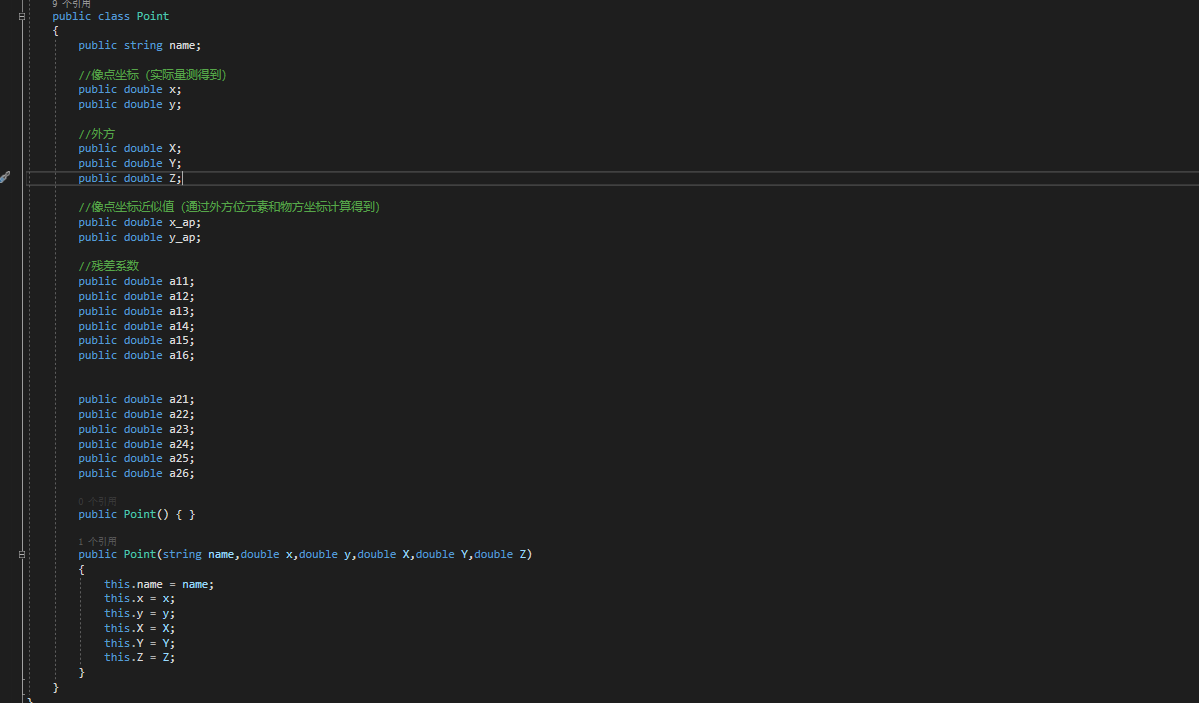
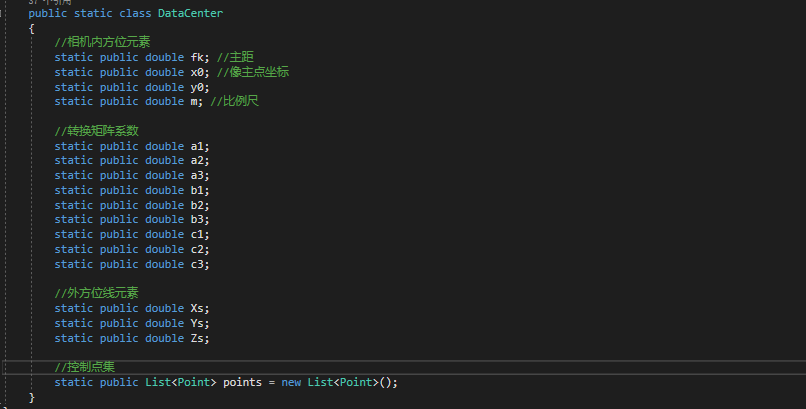
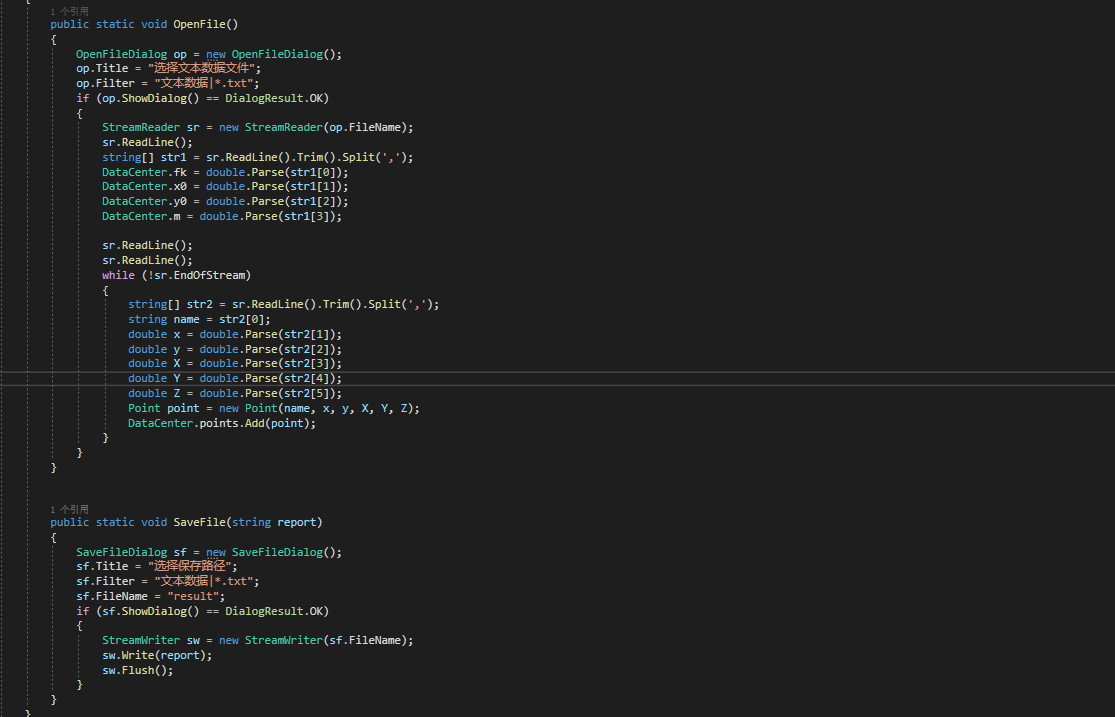
（四）结果

三、唠唠叨叨

先来总结。这道题在干的，就是用已知求参来推未知，和深度学习什么的在拟合和反演上的用意是大差不差的，都是我们拿有限的数据，来推测和繁衍出我们没有的信息。（只不过这个有明确已知的限制参数）。

依旧是首先根据数据来设计数据结构类体，这里小编一个很大的感受就是在程序设计里，定义一个好的数据结构，明白数据是怎么在你的程序里流动的，真的很重要。然后设计算法，这里小编用的就是摄影测量中的常规方法，不过矩阵是真的（省略一万字）。

这道题，考的可能性也不是多大。矩阵相关的方法撑起了核心算法的大半边天，如果真要考，那就可以说是负和博弈了哈哈。

//以下就是小编的唠嗑儿(废话)区

哈哈，现在回看，没想到已经走了这么远了。七月过去的这两周对小编来说可以说是一个多事之秋哈哈，无论是搬迁还是其它一些琐事真的有时候让小编感觉身心俱疲，但是这个过程中，小编收获到的鼓励支持，感受到的幸运，也真的超级多。

可能人就是需要在一些艰难困苦的日子里，才能捕获到那些被忽视的藏在细节里的幸运吧。很感谢我的老师们，很感谢我的前辈们，也很感谢那些比我优秀的我的同伴们。很感谢我的朋友们，也很感谢你们大家。你们都是，在险处稳稳托举着我的力量。当然也要给自己竖一个大拇指，坚持不放弃。

其实走到了今天，于小编个人而言的，参加这场比赛的终极目标，已近乎达成了。唯结果论有其存在的意义，但站在功利之上，对个人能力的淬炼，对自我的提升，一定铺散在日拱一卒的备赛时光和我们的双手碰触键盘时，按键的每一次震颤中。未来十多天，小编要做的就是在已经理解原理的基础上，继续深入，和赛题建立更深层的联结，相信大家也应该都已经或早或晚进入了这个阶段。未来呢，小编有什么新的感悟也会继续把它们做成文章分享给大家，大家有想法也都可以私信或在评论区说说，评论区就是我们的聊天区哈哈。

最后还是想说，小编本人就是半瓶子晃荡（河北话，就是"也啥也不啥"哈哈），在行文逻辑、算法理解、代码实现上一定会存在着大大小小的问题，各位家人们如果觉得哪一部分可以再详细或简略一些呀，如果觉得哪里小编说的稀里糊涂或者存在错误呀···都可以在我们的聊天区分享出来，小编及时改正，及时调整。

作为一个编者，小编给自己的戒训首先就是尊重知识，虚心受教，力争优质。

一起加油。

2025测绘程序设计国赛实战：一轮终章 | 单向后方交会C#实现

前言

一、数据＆原理解析

（一）数据

（二）核心实现方案

旋转矩阵（a1~c3的计算）

像点近似坐标计算

误差方程系数

最小二乘法与矩阵运算（法方程求解）

迭代更新（外方位元素的优化）

（三）小总结

二、C#实现

（一）窗体

（二）核心算法类

（三）各大辅助类

（四）结果

三、唠唠叨叨

旋转矩阵（`a1~c3`的计算）