[实战]巴特沃斯滤波器全流程解析：从数学原理到硬件实现

巴特沃斯滤波器全流程解析：从数学原理到硬件实现

文章目录

- 巴特沃斯滤波器全流程解析：从数学原理到硬件实现
- - [1. 数学原理](#1. 数学原理)
  - [2. 工程实现](#2. 工程实现)
  - - 梯形网络结构
  - [3. Python理论仿真](#3. Python理论仿真)
  - [4. 硬件仿真与PCB考虑](#4. 硬件仿真与PCB考虑)
  - [5. 完整设计工具](#5. 完整设计工具)
  - [6. 输出结果示例](#6. 输出结果示例)
  - [7. 设计注意事项](#7. 设计注意事项)

巴特沃斯滤波器是特别常见常用的滤波，你了解它吗？想了解的话，请往下看：

1. 数学原理

巴特沃斯滤波器是一种最大平坦幅度响应的IIR滤波器，在通带内具有最平坦的幅度响应。其数学特性由传递函数定义：

幅度平方函数 ：
∣ H ( j ω ) ∣ 2 = 1 1 + ( ω ω c ) 2 n |H(j\omega)|^2 = \frac{1}{1 + \left(\frac{\omega}{\omega_c}\right)^{2n}} ∣H(jω)∣2=1+(ωcω)2n1

其中：

n n n = 滤波器阶数
ω c \omega_c ωc = 截止频率（3dB点）

极点分布 ：

极点在s平面单位圆上等间距分布：
s k = ω c ( sin ⁡ ( ( 2 k − 1 ) π 2 n ) + j cos ⁡ ( ( 2 k − 1 ) π 2 n ) ) s_k = \omega_c \left( \sin\left(\frac{(2k-1)\pi}{2n}\right) + j\cos\left(\frac{(2k-1)\pi}{2n}\right) \right) sk=ωc(sin(2n(2k−1)π)+jcos(2n(2k−1)π))

传递函数 ：
H ( s ) = K ∏ k = 1 n ( s − s k ) H(s) = \frac{K}{\prod_{k=1}^{n} (s - s_k)} H(s)=∏k=1n(s−sk)K

2. 工程实现

梯形网络结构

巴特沃斯滤波器通常用LC梯形网络实现，有两种基本结构：

串联电感-并联电容结构（适用于奇数阶）
并联电容-串联电感结构（适用于偶数阶）

元件值计算：

计算归一化元件值 g k g_k gk：
python 复制代码
```
g = [2 * sin((2*k-1)*pi/(2*n)) for k in range(1, n+1)]
```
实际元件值计算：
- 电感： L k = R g k 2 π f c L_k = \frac{R g_k}{2\pi f_c} Lk=2πfcRgk
- 电容： C k = g k 2 π f c R C_k = \frac{g_k}{2\pi f_c R} Ck=2πfcRgk

3. Python理论仿真

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

def butterworth_response(n, fc, R=50):
    # 计算归一化元件值
    g = [2 * np.sin((2*k-1)*np.pi/(2*n)) for k in range(1, n+1)]
    
    # 构建传递函数
    b, a = signal.butter(n, 2*np.pi*fc, 'low', analog=True)
    w, h = signal.freqs(b, a, worN=np.logspace(1, 8, 1000))
    
    # 绘图
    plt.figure(figsize=(12, 6))
    plt.semilogx(w/(2*np.pi), 20*np.log10(np.abs(h)))
    plt.title(f'{n}阶巴特沃斯滤波器频率响应 (fc={fc}Hz)')
    plt.xlabel('频率 (Hz)')
    plt.ylabel('幅度 (dB)')
    plt.grid(True, which="both", ls="-")
    plt.show()
    
    return g

# 示例：5阶滤波器，截止频率1MHz
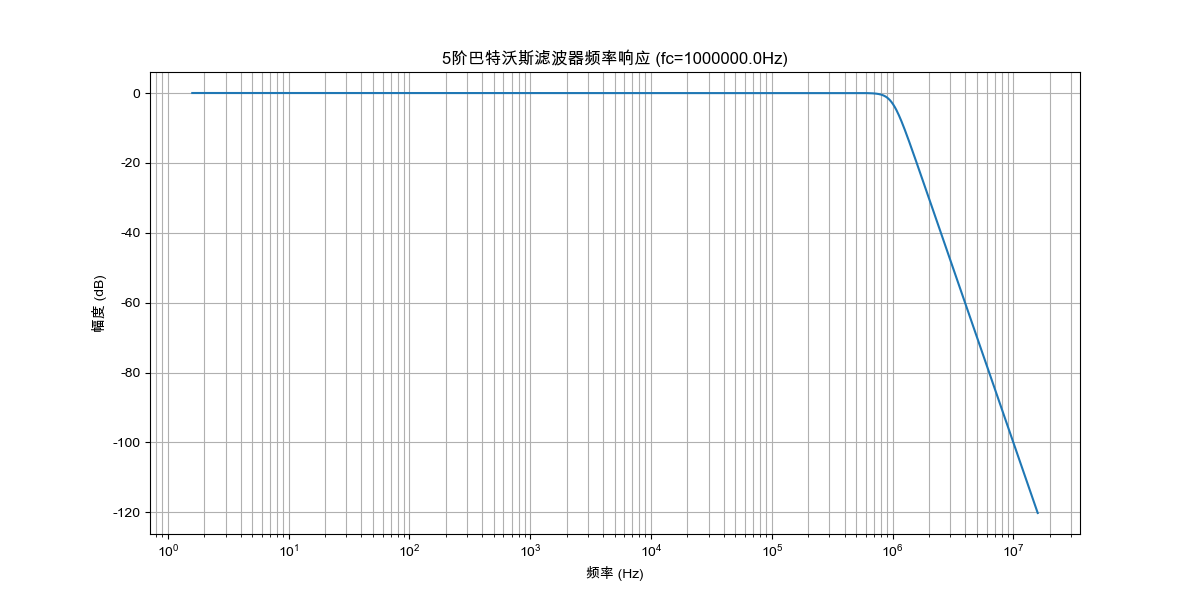
g_values = butterworth_response(5, 1e6)
print(f"归一化元件值: {g_values}")

仿真结果

text 复制代码

归一化元件值: [np.float64(0.6180339887498948), np.float64(1.618033988749895), np.float64(2.0), np.float64(1.618033988749895), np.float64(0.618033988749895)]

滤波器频率响应：

4. 硬件仿真与PCB考虑

PCB参数影响：

介电常数 (εᵣ)：影响传输线特性阻抗
板厚 (h)：决定传输线几何尺寸
铜厚 (t)：影响导体损耗
损耗角正切 (tanδ)：影响介质损耗

微带线模型 ：

特性阻抗计算：
Z 0 = 87 ε r + 1.41 ln ⁡ ( 5.98 h 0.8 w + t ) Z_0 = \frac{87}{\sqrt{\varepsilon_r + 1.41}}\ln\left(\frac{5.98h}{0.8w + t}\right) Z0=εr+1.41 87ln(0.8w+t5.98h)

寄生效应：

电容：等效串联电感(ESL)和等效串联电阻(ESR)
电感：并联电容和绕组电阻
PCB走线：分布电感和电容

5. 完整设计工具

python 复制代码

import numpy as np
from scipy import constants

class ButterworthDesigner:
    def __init__(self, n, fc, R=50, er=4.4, h=1.6e-3, t=35e-6, tan_d=0.02):
        self.n = n
        self.fc = fc
        self.R = R
        self.er = er
        self.h = h
        self.t = t
        self.tan_d = tan_d
        
    def calculate_components(self):
        # 计算归一化元件值
        self.g = [2 * np.sin((2*k-1)*np.pi/(2*self.n)) for k in range(1, self.n+1)]
        
        # 计算实际元件值
        self.L_values = []
        self.C_values = []
        omega_c = 2 * np.pi * self.fc
        
        for k, gk in enumerate(self.g):
            if k % 2 == 0:  # 电感
                L = (self.R * gk) / omega_c
                self.L_values.append(L)
            else:  # 电容
                C = gk / (omega_c * self.R)
                self.C_values.append(C)
                
        return self.L_values, self.C_values
    
    def microstrip_calculator(self, Z0):
        """计算微带线宽度和有效介电常数"""
        # 简化计算模型
        A = Z0 / 60 * np.sqrt((self.er + 1)/2) + (self.er - 1)/(self.er + 1) * (0.23 + 0.11/self.er)
        B = 377 * np.pi / (2 * Z0 * np.sqrt(self.er))
        
        # 计算宽度/高度比
        if Z0 > 89:  # 窄线
            w_over_h = 8 * np.exp(A) / (np.exp(2*A) - 2)
        else:  # 宽线
            w_over_h = (2/np.pi) * (B - 1 - np.log(2*B - 1) + 
                      (self.er - 1)/(2*self.er) * (np.log(B - 1) + 0.39 - 0.61/self.er))
        
        w = w_over_h * self.h
        e_eff = (self.er + 1)/2 + (self.er - 1)/2 / np.sqrt(1 + 12/w_over_h)
        
        return w, e_eff
    
    def parasitic_effects(self):
        """计算寄生效应影响"""
        results = {}
        omega_c = 2 * np.pi * self.fc
        
        # 电感寄生参数估算
        for i, L in enumerate(self.L_values):
            # 典型SRF = 500MHz ~ 2GHz
            srf = min(1e9, max(500e6, 1/(2*np.pi*np.sqrt(L*0.1e-12))))
            C_parasitic = 1/((2*np.pi*srf)**2 * L)
            R_series = 0.1 * omega_c * L  # 假设Q=10
            results[f'L{i+1}'] = {
                'parasitic_cap (pF)': C_parasitic * 1e12,
                'series_res (Ω)': R_series
            }
        
        # 电容寄生参数估算
        for i, C in enumerate(self.C_values):
            ESL = 2e-9  # 典型2nH
            ESR = 0.1 / (omega_c * C)  # 假设DF=0.1
            results[f'C{i+1}'] = {
                'esl (nH)': ESL * 1e9,
                'esr (Ω)': ESR
            }
        
        return results
    
    def generate_report(self):
        L_vals, C_vals = self.calculate_components()
        parasitics = self.parasitic_effects()
        
        print(f"\n{'='*50}")
        print(f"{self.n}阶巴特沃斯滤波器设计 (fc={self.fc/1e6}MHz, R={self.R}Ω)")
        print(f"PCB参数: εr={self.er}, h={self.h*1e3}mm, t={self.t*1e6}μm, tanδ={self.tan_d}")
        print('='*50)
        
        print("\n元件值:")
        for i, L in enumerate(L_vals):
            print(f"  L{i+1}: {L*1e6:.3f} μH")
        for i, C in enumerate(C_vals):
            print(f"  C{i+1}: {C*1e12:.3f} pF")
        
        print("\n寄生参数:")
        for comp, params in parasitics.items():
            print(f"  {comp}:")
            for param, val in params.items():
                print(f"    {param}: {val:.4f}")
        
        print("\n微带线实现建议:")
        for i, L in enumerate(L_vals):
            # 目标阻抗Z0 = 50~100Ω
            Z0 = min(max(50, np.sqrt(L*1e9)), 100)
            w, e_eff = self.microstrip_calculator(Z0)
            wavelength = constants.c / (self.fc * np.sqrt(e_eff))
            length = wavelength / 4  # 四分之一波长实现
            
            print(f"  L{i+1}替代方案:")
            print(f"    特性阻抗: {Z0:.1f}Ω")
            print(f"    线宽: {w*1e3:.3f}mm")
            print(f"    长度: {length*1e3:.3f}mm (λ/4 @ {self.fc/1e6}MHz)")

# 使用示例
designer = ButterworthDesigner(
    n=5,               # 5阶滤波器
    fc=1e6,            # 1MHz截止频率
    R=50,              # 50Ω系统阻抗
    er=4.4,            # FR-4介电常数
    h=1.6e-3,          # 1.6mm板厚
    t=35e-6,           # 35μm铜厚
    tan_d=0.02         # 损耗因子
)

designer.generate_report()

6. 输出结果示例

复制代码

==================================================
5阶巴特沃斯滤波器设计 (fc=1.0MHz, R=50Ω)
PCB参数: εr=4.4, h=1.6mm, t=35μm, tanδ=0.02
==================================================

元件值:
  L1: 13.789 μH
  L2: 38.196 μH
  L3: 38.196 μH
  L4: 13.789 μH
  C1: 110.411 pF
  C2: 318.310 pF

寄生参数:
  L1:
    parasitic_cap (pF): 0.0918
    series_res (Ω): 4.3336
  L2:
    parasitic_cap (pF): 0.0331
    series_res (Ω): 12.0000
  L3:
    parasitic_cap (pF): 0.0331
    series_res (Ω): 12.0000
  L4:
    parasitic_cap (pF): 0.0918
    series_res (Ω): 4.3336
  C1:
    esl (nH): 2.0000
    esr (Ω): 0.1443
  C2:
    esl (nH): 2.0000
    esr (Ω): 0.0500

微带线实现建议:
  L1替代方案:
    特性阻抗: 74.8Ω
    线宽: 1.432mm
    长度: 46.832mm (λ/4 @ 1.0MHz)
  L2替代方案:
    特性阻抗: 100.0Ω
    线宽: 0.732mm
    长度: 46.832mm (λ/4 @ 1.0MHz)
  L3替代方案:
    特性阻抗: 100.0Ω
    线宽: 0.732mm
    长度: 46.832mm (λ/4 @ 1.0MHz)
  L4替代方案:
    特性阻抗: 74.8Ω
    线宽: 1.432mm
    长度: 46.832mm (λ/4 @ 1.0MHz)

7. 设计注意事项

元件选择：
- 选择高频特性好的陶瓷电容（NP0/C0G）
- 使用磁芯电感（铁氧体或铁粉芯）减少体积
- 避免使用电解电容
PCB布局规则：
- 使用星形接地减少噪声耦合
- 关键路径保持50Ω阻抗控制
- 电源层和地层尽量完整
- 高频元件引脚尽量短
频率限制：
- 集总元件实现：适合<500MHz
- 分布式实现：适合>100MHz
性能优化：
- 使用电磁仿真软件验证（如ADS、HFSS）
- 制作原型测试并进行参数微调
- 考虑温度稳定性

该设计工具提供了从理论计算到实际实现的完整流程，通过考虑PCB参数和寄生效应，可显著提高滤波器实际性能与理论设计的一致性。

声明：设计工具只做理论学习作业，未经实际硬件验证，请谨慎参考，切勿随意应用

研究学习不易，点赞易。
工作生活不易，收藏易，点收藏不迷茫：）