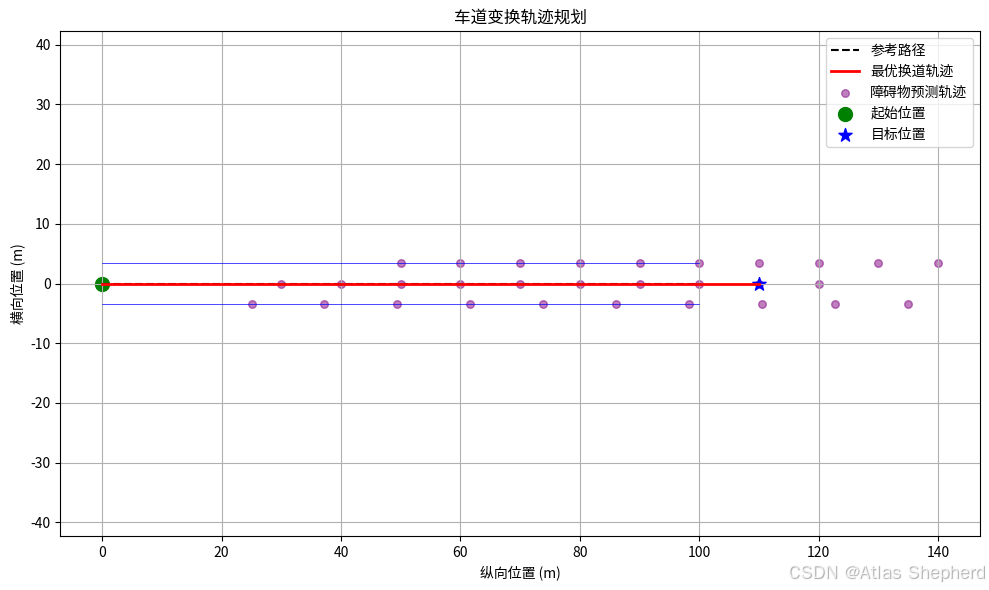
基于Frenet坐标系的车道变换轨迹规划器,适用于自动驾驶或路径规划场景。以下是代码的结构和功能分析:
1. 核心类与功能
1.1 FrenetConverter 类
功能:在Frenet坐标系(s, d)和笛卡尔坐标系(x, y)之间进行转换。
-
属性:
ref_path: 由起点和终点生成的参考路径(直线)。s_coords: 每个参考路径点的累计纵向距离(s)。spline: 三次样条插值,用于将s映射到笛卡尔坐标。
-
方法:
cartesian_to_frenet(point):- 找到参考路径上距离
point最近的点。 - 根据该点的切向量计算法向量,得到横向偏移
d。
- 找到参考路径上距离
frenet_to_cartesian(s, d):- 使用样条插值获得参考点的笛卡尔坐标。
- 根据切向量计算法向量,加上
d得到最终位置。
用途:将轨迹规划从Frenet坐标系转换为实际的笛卡尔坐标,便于可视化和避障。
1.2 LaneChangePlanner 类
功能:生成并评估车道变换轨迹,选择最优路径。
-
属性:
ego_car: 自车的初始状态(x, y, v, heading)。obs: 障碍物的状态列表(每个障碍物为[x, y, v, heading])。ref_path: 参考路径(用于生成Frenet坐标)。
-
方法:
generate_lateral_trajectories():- 使用多项式拟合生成横向轨迹(d方向),目标是实现车道变换。
generate_longitudinal_trajectories():- 生成纵向轨迹(s方向),表示自车的前进路径。
initial_screening():- 筛选满足加速度、jerk、曲率约束的轨迹。
risk_field():- 计算轨迹与障碍物的碰撞风险,使用指数衰减模型。
efficiency_metric():- 用纵向位移增量衡量轨迹效率。
comfort_metric():- 用横向jerk的均方根倒数衡量舒适度。
evaluate_trajectory():- 综合安全、效率、舒适度指标,加权评分。
select_optimal_trajectory():- 生成候选轨迹,筛选并选择最优路径。
visualize():- 可视化参考路径、车道线、自车轨迹、障碍物预测轨迹。
2. 代码流程
-
初始化:
- 设置自车状态、障碍物状态和参考路径。
-
轨迹生成:
- 使用多项式拟合生成横向(d)和纵向(s)轨迹,组合成候选轨迹。
-
初步筛选:
- 检查轨迹是否满足加速度、jerk、曲率约束。
-
综合评估:
- 计算轨迹的安全风险 、效率 、舒适度,加权求和得到评分。
-
选择最优轨迹:
- 根据评分选择最优轨迹,并输出轨迹点坐标。
-
可视化:
- 绘制参考路径、车道线、自车轨迹、障碍物预测轨迹。
import numpy as np
from scipy.spatial.distance import cdist
from scipy.interpolate import CubicSpline
import matplotlib.pyplot as pltclass FrenetConverter:
"""Frenet坐标系转换工具(直线参考路径简化版)"""
def init(self, start_point, end_point):
self.ref_path = np.linspace(start_point, end_point, 100)
self.s_coords = np.cumsum(np.sqrt(np.sum(np.diff(self.ref_path, axis=0)**2, axis=1)))
self.s_coords = np.insert(self.s_coords, 0, 0)
self.spline = CubicSpline(self.s_coords, self.ref_path)def cartesian_to_frenet(self, point): """笛卡尔坐标转Frenet坐标""" dists = cdist([point], self.ref_path) min_idx = np.argmin(dists) s = self.s_coords[min_idx] # 计算法向距离 tangent = self.ref_path[min_idx] - self.ref_path[min_idx-1] if min_idx > 0 else self.ref_path[1] - self.ref_path[0] normal = np.array([-tangent[1], tangent[0]]) normal /= np.linalg.norm(normal) d = np.dot(point - self.ref_path[min_idx], normal) return s, d def frenet_to_cartesian(self, s, d): """Frenet坐标转笛卡尔坐标""" ref_point = self.spline(s) if len(ref_point) > 2: ref_point = ref_point[:, 0] # 计算法向向量 tangent = self.spline(s, 1) # 一阶导数(切向量) if tangent[0] == 0 and tangent[1] == 0: # 防止零切向量 tangent = np.array([1e-5, 0]) normal = np.array([-tangent[1], tangent[0]]) normal /= np.linalg.norm(normal) return ref_point + d * normalclass LaneChangePlanner:
def init(self, ego_car, obstacles, ref_path=None, dt=0.1, T=5.0):
"""
初始化参数
ego_car: 自车状态 [x, y, v, heading]
obstacles: 障碍车列表 [[x, y, v, heading], ...]
ref_path: 参考路径 [(x0,y0), (x1,y1), ...]
dt: 时间步长
T: 换道总时间
"""
self.ego = ego_car
self.obs = obstacles
self.dt = dt
self.T = T
self.time_steps = int(T / dt)# 安全阈值参数 self.safe_distance = 5.0 # 最小安全距离 self.max_accel = 3.0 # 最大加速度(m/s²) self.max_jerk = 5.0 # 最大加加速度(m/s³) self.max_curv = 0.2 # 最大曲率(1/m) self.max_steering = 0.5 # 最大转向角 # 设置默认参考路径(直线) if ref_path is None: ref_path = np.array([[0, 0], [200, 0]]) self.ref_converter = FrenetConverter(ref_path[0], ref_path[-1]) # 目标车道横向位移(正常3.5米车道) self.target_d = 3.5 if self.ego[1] < 0 else -3.5 def predict_obstacle(self, ob_state, t): """预测障碍车t秒后的位置(匀速直线模型)""" x, y, v, heading = ob_state distance = v * t return np.array([ x + distance * np.cos(heading), y + distance * np.sin(heading) ]) def calc_curvature(self, s_traj, d_traj): """计算轨迹曲率(Frenet坐标系下)""" t = np.arange(len(s_traj)) * self.dt # 计算导数 v_s = np.gradient(s_traj, t) # 纵向速度 a_s = np.gradient(v_s, t) # 纵向加速度 v_d = np.gradient(d_traj, t) # 横向速度 a_d = np.gradient(v_d, t) # 横向加速度 # 计算曲率(近似公式) curv = np.abs(a_d) / (v_s**2 + 1e-5) # 防止除以0 return curv def generate_lateral_trajectories(self): """生成横向轨迹簇(五次多项式)""" t = np.linspace(0, self.T, self.time_steps) _, d0 = self.ref_converter.cartesian_to_frenet(self.ego[:2]) v_d0 = self.ego[3] # 初始横向速度 # 横向位移目标范围 target_d_min = max(0, self.target_d - 0.5) target_d_max = min(0, self.target_d + 0.5) trajectories = [] coeffs_list = [] # 采样不同的终端状态 for d_end in np.linspace(target_d_min, target_d_max, 5): # 五次多项式系数 (d(t) = a0 + a1*t + a2*t² + a3*t³ + a4*t⁴ + a5*t⁵) A = np.array([ [1, 0, 0, 0, 0, 0], # d(0) = d0 [0, 1, 0, 0, 0, 0], # d'(0) = v_d0 [0, 0, 2, 0, 0, 0], # d''(0) = 0 (默认初始加速度为0) [1, self.T, self.T**2, self.T**3, self.T**4, self.T**5], [0, 1, 2*self.T, 3*self.T**2, 4*self.T**3, 5*self.T**4], [0, 0, 2, 6*self.T, 12*self.T**2, 20*self.T**3] ]) b = np.array([d0, v_d0, 0, d_end, 0, 0]) # 终端速度和加速度为0 try: coeffs = np.linalg.solve(A, b)[::-1] # 翻转顺序用于polyval d_traj = np.polyval(coeffs, t) trajectories.append(d_traj) coeffs_list.append(coeffs) except np.linalg.LinAlgError: continue return trajectories, coeffs_list def generate_longitudinal_trajectories(self): """生成纵向轨迹簇(四次多项式)""" t = np.linspace(0, self.T, self.time_steps) s0, _ = self.ref_converter.cartesian_to_frenet(self.ego[:2]) v_s0 = self.ego[2] # 初始纵向速度 trajectories = [] # 采样不同的终端速度 for v_end in np.linspace(self.ego[2]*0.8, self.ego[2]*1.2, 5): # 四次多项式 (s(t) = a0 + a1*t + a2*t² + a3*t³ + a4*t⁴) # 边界条件: s(0)=s0, s'(0)=v_s0, s'(T)=v_end, s''(0)=0, s''(T)=0 A = np.array([ [1, 0, 0, 0, 0], [0, 1, 0, 0, 0], [0, 0, 2, 0, 0], [0, 1, 2*self.T, 3*self.T**2, 4*self.T**3], [0, 0, 2, 6*self.T, 12*self.T**2] ]) b = np.array([s0, v_s0, 0, v_end, 0]) try: coeffs = np.linalg.solve(A, b)[::-1] s_traj = np.polyval(coeffs, t) trajectories.append(s_traj) except np.linalg.LinAlgError: continue return trajectories def initial_screening(self, s_trajs, d_trajs): """基于动力学约束的初筛""" valid_trajs = [] for s_traj in s_trajs: for d_traj in d_trajs: t = np.arange(len(s_traj)) * self.dt # 纵向动力学约束 v_s = np.gradient(s_traj, t) a_s = np.gradient(v_s, t) jerk_s = np.gradient(a_s, t) # 横向动力学约束 v_d = np.gradient(d_traj, t) a_d = np.gradient(v_d, t) jerk_d = np.gradient(a_d, t) # 组合约束检查 if (np.max(np.abs(a_s)) < self.max_accel and np.max(np.abs(jerk_s)) < self.max_jerk and np.max(np.abs(a_d)) < self.max_accel and np.max(np.abs(jerk_d)) < self.max_jerk): # 曲率约束检查 curv = self.calc_curvature(s_traj, d_traj) if np.max(np.abs(curv)) < self.max_curv: valid_trajs.append((s_traj, d_traj)) return valid_trajs def risk_field(self, traj): """计算轨迹风险值""" total_risk = 0 s_traj, d_traj = traj for i, (s, d) in enumerate(zip(s_traj, d_traj)): t = i * self.dt ego_pos = self.ref_converter.frenet_to_cartesian(s, d) for ob in self.obs: # 预测障碍车位置 ob_pos = self.predict_obstacle(ob, t) # 计算欧氏距离 distance = np.linalg.norm(ego_pos - ob_pos) # 风险函数(指数衰减模型) if distance < self.safe_distance: risk = np.exp(-distance/self.safe_distance * 3) total_risk += risk return total_risk def efficiency_metric(self, s_traj): """计算效率指标""" # 纵向位移增量作为效率衡量(越大越好) return s_traj[-1] - s_traj[0] def comfort_metric(self, d_traj): """计算舒适度指标""" t = np.arange(len(d_traj)) * self.dt # 横向加速度变化率(jerk) v_d = np.gradient(d_traj, t) a_d = np.gradient(v_d, t) jerk_d = np.gradient(a_d, t) # 舒适度反比于jerk的均方根 return 1 / (np.sqrt(np.mean(jerk_d**2)) + 1e-5) def evaluate_trajectory(self, traj): """轨迹综合评价""" s_traj, d_traj = traj # 安全指标(风险越低越好) safety_score = -self.risk_field(traj) # 效率指标(纵向位移越大越好) efficiency_score = self.efficiency_metric(s_traj) # 舒适度指标(横向jerk越小越好) comfort_score = self.comfort_metric(d_traj) # 归一化权重 safety_score = safety_score * 0.6 efficiency_score = efficiency_score * 0.3 comfort_score = comfort_score * 0.1 return safety_score + efficiency_score + comfort_score def select_optimal_trajectory(self): """主规划函数""" # 生成轨迹簇 lat_trajs, _ = self.generate_lateral_trajectories() lon_trajs = self.generate_longitudinal_trajectories() # 组合横纵向轨迹 candidate_trajs = [] for s_traj in lon_trajs: for d_traj in lat_trajs: candidate_trajs.append((s_traj, d_traj)) # 初筛 valid_trajs = self.initial_screening( [t[0] for t in candidate_trajs], [t[1] for t in candidate_trajs] ) if not valid_trajs: raise RuntimeError("未找到满足动力学约束的轨迹") # 评估并选择最优 best_score = -np.inf best_traj = None for traj in valid_trajs: score = self.evaluate_trajectory(traj) if score > best_score: best_score = score best_traj = traj return best_traj def visualize(self, best_traj): """可视化最佳轨迹""" s_traj, d_traj = best_traj # 转换到笛卡尔坐标系 cartesian_traj = [] for s, d in zip(s_traj, d_traj): cartesian_traj.append(self.ref_converter.frenet_to_cartesian(s, d)) cartesian_traj = np.array(cartesian_traj) # 障碍物轨迹 obstacle_traj = [] for ob in self.obs: for t in np.linspace(0, self.T, 10): obstacle_traj.append(self.predict_obstacle(ob, t)) obstacle_traj = np.array(obstacle_traj) plt.figure(figsize=(10, 6)) # 绘制参考路径 plt.plot(self.ref_converter.ref_path[:, 0], self.ref_converter.ref_path[:, 1], 'k--', label='参考路径') # 绘制车道线 plt.plot(self.ref_converter.ref_path[:, 0], self.ref_converter.ref_path[:, 1] + 3.5, 'b-', linewidth=0.5) plt.plot(self.ref_converter.ref_path[:, 0], self.ref_converter.ref_path[:, 1] - 3.5, 'b-', linewidth=0.5) # 绘制自车轨迹 plt.plot(cartesian_traj[:, 0], cartesian_traj[:, 1], 'r-', linewidth=2, label='最优换道轨迹') # 绘制障碍物轨迹 if obstacle_traj.any(): plt.scatter(obstacle_traj[:, 0], obstacle_traj[:, 1], c='purple', s=30, alpha=0.5, label='障碍物预测轨迹') # 绘制起点和终点 plt.scatter(cartesian_traj[0, 0], cartesian_traj[0, 1], s=100, c='green', marker='o', label='起始位置') plt.scatter(cartesian_traj[-1, 0], cartesian_traj[-1, 1], s=100, c='blue', marker='*', label='目标位置') plt.title('车道变换轨迹规划') plt.xlabel('纵向位置 (m)') plt.ylabel('横向位置 (m)') plt.legend() plt.grid(True) plt.axis('equal') plt.tight_layout() plt.show()===== 测试用例 =====
if name == "main":
# 初始化车辆状态
ego_car = [0, 0, 20, 0] # [x, y, v, heading]# 障碍物状态 [x, y, v, heading] obstacles = [ [30, 0, 18, 0], # 同车道前车 [25, -3.5, 22, 0], # 目标车道后车 [50, 3.5, 18, 0] # 目标车道前车 ] # 参考路径(直线) ref_path = np.array([[0, 0], [100, 0]]) # 创建规划器 planner = LaneChangePlanner(ego_car, obstacles, ref_path) try: # 执行轨迹规划 optimal_traj = planner.select_optimal_trajectory() s_traj, d_traj = optimal_traj # 输出轨迹点 print("最优轨迹点序列:") for i, (s, d) in enumerate(zip(s_traj, d_traj)): cart_pos = planner.ref_converter.frenet_to_cartesian(s, d) print(f"t={i*planner.dt:.1f}s: 位置=({cart_pos[0]:.2f}, {cart_pos[1]:.2f})m, " f"s={s:.2f}m, d={d:.2f}m") # 可视化结果 planner.visualize(optimal_traj) except RuntimeError as e: print(f"轨迹规划失败: {e}")