[论文阅读] 人工智能 | ZipMPC：让短视的MPC拥有长远眼光——通过模仿学习压缩长 horizon 智慧

ZipMPC：让短视的MPC拥有长远眼光------通过模仿学习压缩长 horizon 智慧

论文标题：ZipMPC: Compressed Context-Dependent MPC Cost via Imitation Learning

arXiv:2507.13088 [pdf, ps, other] cs.RO eess.SY

ZipMPC: Compressed Context-Dependent MPC Cost via Imitation Learning

Authors: Rahel Rickenbach, Alan A. Lahoud, Erik Schaffernicht, Melanie N. Zeilinger, Johannes A. Stork

一段话总结

ZipMPC 是一种通过模仿学习实现长预测 horizon 模型预测控制（MPC）行为的方法，其核心是为短 horizon MPC 学习一个压缩的、上下文相关的成本函数，以解决传统MPC在实时系统（如机器人）中因计算负担重而限制应用的问题。该方法利用可微分MPC和神经网络传播模仿损失的梯度，兼具短 horizon MPC的计算效率、长 horizon MPC的长期目标优化能力、约束满足性及对未训练环境的泛化能力。在自主赛车的仿真和实车实验中，ZipMPC的圈速接近长 horizon MPC，且优于短 horizon MPC和其他基线方法（如eMPC、BO），甚至能完成短 horizon MPC无法完成的赛道任务。

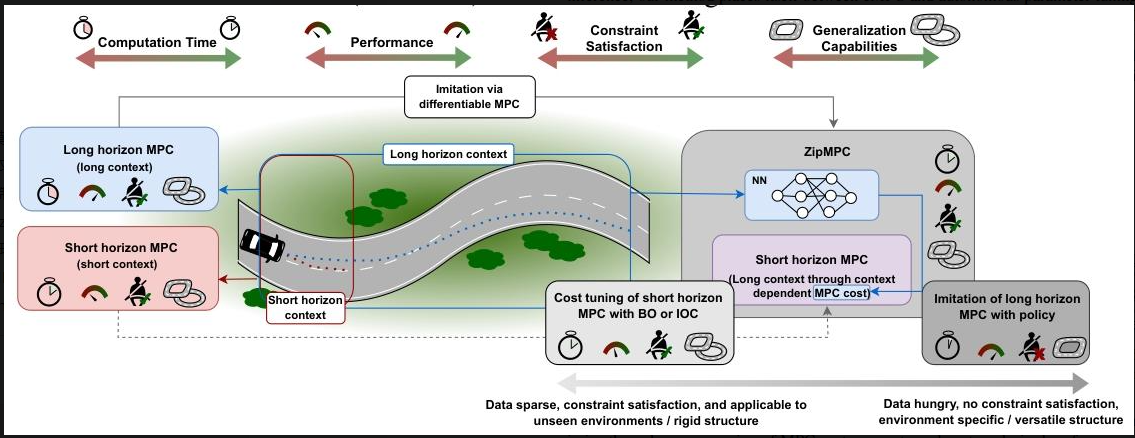
研究背景：MPC的"短视"困境与行业痛点

想象一下，当一辆自动驾驶赛车飞驰在赛道上时，它需要每秒多次决策下一步的转向和加速。如果它只看眼前10米的路况（短预测范围，即短horizon），很可能在即将到来的急弯前减速过晚，甚至冲出赛道；但如果它能看到前方100米的全部弯道（长horizon），就能提前规划最优路线，跑得又快又稳。

这正是模型预测控制（MPC）在实际应用中面临的核心矛盾：长horizon MPC能优化长期目标，性能更优，但计算量太大，无法满足实时性要求；短horizon MPC计算快，却因"目光短浅"导致性能差，且成本函数设计难度极高。

在机器人、自动驾驶等领域，这个矛盾尤为突出。比如自主赛车，短horizon MPC可能因无法预判弯道而频繁急刹，长horizon MPC虽能平滑过弯，却因计算太慢跟不上实时控制需求。现有解决方案也各有缺陷：近似显式MPC（eMPC）计算快但泛化差，换个赛道就"失灵"；贝叶斯优化（BO）或逆最优控制（IOC）调参无法利用长horizon的上下文信息，填不上"信息缺口"。

行业迫切需要一种方法：既能像短horizon MPC一样"反应迅速"，又能像长horizon MPC一样"高瞻远瞩"。

主要作者及单位

该研究由来自瑞士苏黎世联邦理工学院（ETH Zurich）和瑞典厄勒布鲁大学（Örebro University）的团队合作完成，核心作者包括Rahel Rickenbach、Alan A. Lahoud、Melanie N. Zeilinger等。相关代码和视频可在zipmpc.github.io/查看。

创新点：用"模仿学习"给短horizon MPC装"长焦镜头"

ZipMPC的核心创新在于：让短horizon MPC通过模仿长horizon MPC的行为，学会利用长horizon的上下文信息，同时保持自身计算效率。具体来说，它通过三个关键设计打破传统局限：

压缩长horizon信息：用神经网络将长horizon的上下文（如赛道曲率序列）编码成短horizon MPC的成本函数参数，相当于给短horizon MPC装上"记忆"，让它"记住"远方的路况。
可微分MPC传梯度：借助可微分MPC技术，将"模仿损失"（短horizon与长horizon轨迹的差距）的梯度穿过MPC优化过程，精准更新神经网络，确保学到的成本函数真能模仿长horizon的决策。
兼顾灵活性与约束：不直接学控制策略（如行为克隆），而是学成本函数，既保证了对新环境的泛化能力，又能通过MPC本身的优化过程满足系统约束（如赛车不冲出赛道）。

简单说，ZipMPC就像一个"聪明的实习生"：通过观察"资深专家"（长horizon MPC）的决策逻辑，把复杂经验浓缩成简单规则（成本函数），自己干活（短horizon MPC）时又快又好。

研究方法：从模仿到落地的完整路径

ZipMPC的实现逻辑可以拆解为四个核心步骤，从目标定义到实验验证环环相扣：

步骤1：明确"模仿目标"

定义长horizon MPC（NLN_LNL）为"老师"，其优化结果（轨迹和控制输入）作为模仿目标；短horizon MPC（NSN_SNS，NS<NLN_S < N_LNS<NL）为"学生"，目标是通过学习成本函数，让自己的轨迹尽可能接近老师。

步骤2：设计"模仿工具"

用神经网络（参数θ\thetaθ）构建函数hθh^\thetahθ，输入当前状态（如赛车位置、速度）和长horizon上下文（如未来赛道曲率），输出短horizon MPC的成本参数CNSθC_{N_S}^\thetaCNSθ。
为了让学习更高效，以人工设计的短horizon成本参数为"起点"，神经网络只输出修正值，最终成本参数为"起点+修正值"。

步骤3：优化"模仿效果"

用均方误差（MSE）计算短horizon与长horizon轨迹的"模仿损失"，重点关注前NDN_DND步（ND≤NSN_D \leq N_SND≤NS），因为MPC实际只执行第一步控制输入。
用Adam优化器更新神经网络参数，通过可微分MPC确保梯度能从损失反向传播到网络权重，避免"学歪"。

步骤4：实验验证

在自主赛车场景中测试：

仿真：用运动学模型（简单）和Pacejka模型（复杂，考虑轮胎力学）对比ZipMPC与短horizon MPC、eMPC、BO等基线的模仿误差、圈速和计算时间。
硬件：在微型赛车平台上验证，不重新训练直接部署仿真中得到的模型，测试实际赛道表现。

核心成果：性能、效率与泛化的全面突破

ZipMPC在仿真和硬件实验中均展现出显著优势，完美解决了传统方法的痛点：

1. 性能逼近长horizon，效率看齐短horizon

在自主赛车仿真中，当NS=5N_S=5NS=5、NL=18N_L=18NL=18时，ZipMPC的轨迹模仿误差（RMSE）仅0.065，远低于短horizon MPC（0.194）和BO（0.089）。
圈速上，ZipMPC接近长horizon MPC（如运动学模型中，长horizon圈速8.358s，ZipMPC 8.436s），但计算时间仅为长horizon的17.5%~29%。

2. 能完成"不可能的任务"

在Pacejka模型中，短horizon MPC（NS=6N_S=6NS=6）因"短视"无法完成赛道，而ZipMPC（NS=6N_S=6NS=6）借助长horizon上下文信息，不仅能完成，还能将圈速控制在13.83s左右。

3. 泛化能力强，新赛道也能跑

在未训练的赛道（更长、曲率更复杂）上，ZipMPC的圈速仍显著低于短horizon MPC。例如运动学模型中，测试赛道1的短horizon圈速6.891s，ZipMPC为6.312s，接近长horizon的6.273s。

4. 硬件落地验证

在微型赛车实验中，ZipMPC的轨迹更平滑（减少急刹急转），圈速比短horizon MPC更优，甚至能在短horizon MPC"卡壳"的弯道中顺利通过。

思维导图

详细总结

1. 研究背景与挑战

MPC的应用与局限：MPC在机器人、自主赛车等安全关键领域应用广泛，但为保证实时性常采用短预测 horizon，导致长期目标优化能力弱、成本函数设计困难。
现有方法的不足 ：
- 近似显式MPC（eMPC）：计算快但泛化差，难以满足约束；
- 成本参数调优（BO/IOC）：无法利用长horizon上下文信息，难以弥补信息缺口。

2. ZipMPC的核心设计

核心思想：通过模仿学习，让短horizon MPC（Ns）学习长horizon MPC（NL，NL>Ns）的行为，具体是用神经网络学习一个依赖状态和长horizon上下文（如赛道曲率）的成本函数，压缩长horizon信息到短horizon中。
学习框架 ：
- 输入：当前状态x(k)和长horizon上下文Zk,NL（如赛道曲率序列）；
- 输出：短horizon成本参数CNs^{θ，通过神经网络h}θ计算（CNs^θ = h^θ(x(k), Zk,NL)）；
- 优化目标：最小化短horizon轨迹与长horizon轨迹的模仿损失（如MSE）。
梯度传播：利用可微分MPC技术（如基于KKT条件的iLQR近似），将损失梯度通过MPC优化过程传播到神经网络参数，实现端到端训练。

3. 实验结果

实验指标	关键结果（以自主赛车为例）
模仿误差	ZipMPC的RMSE显著低于BO、eMPC和短horizon MPC，如Ns=5、NL=18时，ZipMPC为0.065±0.006，BO为0.089±0.009
圈速性能	接近长horizon MPC，优于其他方法。如运动学模型中，Ns=5、NL=18时，ZipMPC圈速8.436s，短horizon MPC为9.103s
计算效率	优化时间较长期MPC减少82.5%~87.9%（Pacejka模型，Ns=6、NL=35/45时）
泛化能力	在未训练赛道（更长/更短、曲率不同）上，圈速仍低于短horizon MPC，如运动学模型中测试赛道1的圈速6.312s vs 6.891s
约束满足	能完成短horizon MPC无法完成的赛道（如Pacejka模型中Ns=6时，短horizon MPC失败，ZipMPC成功）

4. 结论与局限性

结论：ZipMPC结合了eMPC的计算效率、BO/IOC的约束满足与泛化能力，在自主赛车任务中验证了其优越性。
局限性：依赖可微分MPC的性能、对不可行初始状态敏感、模仿损失非凸可能导致局部最优。

4. 关键问题

ZipMPC如何实现短horizon MPC对长horizon MPC的模仿？

答：ZipMPC通过神经网络（参数θ）将长horizon上下文信息（如赛道曲率序列Zk,NL）和当前状态x(k)编码为短horizon MPC的成本参数CNs^θ，再利用可微分MPC技术传播模仿损失（短horizon与长horizon轨迹的MSE）的梯度，优化神经网络权重，使短horizon MPC的行为接近长horizon MPC。
与短horizon MPC、eMPC等基线方法相比，ZipMPC的核心优势是什么？

答：相比短horizon MPC，ZipMPC通过引入长horizon上下文信息，优化了长期目标，提升了圈速并能完成其无法完成的任务；相比eMPC，ZipMPC保留了约束满足性且泛化能力更强（能适应未训练环境）；同时保持与短horizon MPC相当的计算效率。
实验中ZipMPC在自主赛车上的性能提升具体体现在哪些方面？

答：① 圈速更接近长horizon MPC（如运动学模型中，ZipMPC圈速8.436s vs 长horizon 8.358s）；② 计算时间显著减少（如Pacejka模型中减少82.5%~87.9%）；③ 在未训练赛道上仍保持优势（如测试赛道圈速降低约8%）；④ 能完成短horizon MPC和eMPC无法完成的赛道。

总结：从"鱼和熊掌"到"两全其美"

ZipMPC的核心价值，在于打破了MPC中"计算效率"与"控制性能"的对立：它用模仿学习压缩长horizon的智慧，用可微分MPC保证学习精度，最终让短horizon MPC既能"跑得快"（计算快），又能"看得远"（性能优）。

对于自主赛车、机器人等实时系统，这意味着更低的硬件成本（无需高性能计算单元）和更高的任务可靠性（适应新环境、满足约束）。未来随着可微分MPC技术的进步，其在更复杂场景（如多机器人协作）中的潜力将进一步释放。