基于物理的天空、大气与云渲染在 Frostbite 引擎中的应用

Mr_Swilder2025-07-23 15:39

以下是对《Physically Based Sky, Atmosphere and Cloud Rendering in Frostbite》技术文档的全文逐行翻译，保留原始结构和专业术语，严格遵循图片标签嵌入规则：

​Sébastien Hillaire ​
EA Frostbite

​目录​

  1. 引言
    1.1 背景
    1.2 范围与目标
    1.3 贡献者
  2. 参与介质
    2.1 单次散射
    2.2 反照率
    2.3 相位函数
    2.3.1 各向同性散射相位
    2.3.2 瑞利散射相位
    2.3.3 米氏散射相位
    2.3.4 几何散射相位
    2.4 示例
    2.5 相关章节
  3. 天空与大气
    3.1 先前工作
    3.2 天空与大气参与介质的定义
    3.3 大气成分
    3.4 臭氧吸收
    3.5 我们的方法
    3.5.1 性能
    3.5.2 结果
  4. 太阳、月亮与星辰
    4.1 太阳
    4.1.1 太阳照度
    4.1.2 太阳亮度
    4.1.3 临边昏暗
    4.2 月亮
    4.3 星辰
    4.4 结果
  5. 云
    5.1 背景与先前工作
    5.2 云参与介质材质
    5.3 云的创作
    5.3.1 云的分布与密度
    5.4 云噪声
    5.4.1 云材质
    5.5 云渲染
    5.5.1 环境光照
    5.5.2 太阳阴影采样
    5.5.3 时间散射积分
    5.6 改进的散射
    5.6.1 常规散射积分
    5.6.2 更优数值积分
    5.6.3 能量守恒分析积分
    5.7 云相位函数
    5.8 多次散射
    5.9 其他交互
    5.9.1 大气透视对云的影响
    5.9.2 云对大气透视的影响
    5.10 性能
    5.11 结果
  6. 结论
    6.1 未来工作
    附录 A 天空查找表参数化
    附录 B 太阳临边昏暗天体物理模型
    附录 C 能量守恒分析散射积分
    附录 D 平铺体积噪声库

​1 引言​

电子游戏对视觉质量和动态性的要求日益提高。开放世界游戏需要大量动态元素，如随时间变化的光照和实时演变的天气。这些元素的动态性和全局性使其难以实时模拟和渲染。​天空、大气和云是实现动态时间和天气条件的三大核心要素，其详细的体积特性使渲染变得复杂，且三者相互影响（如云影响大气光照，反之亦然）。

本文介绍 Frostbite 引擎中基于物理的解决方案，涵盖这些元素的模拟、组合及交互渲染，并说明其如何融入引擎的物理着色框架，以及艺术家创作流程与性能特征。

​1.1 背景​

2014年，Frostbite 全面升级为基于物理的渲染引擎[LR14]，实现了光照与材质的解耦，提升了视觉质量（图1）。然而，天空、雾、云等系统仍为静态元素，需艺术家手动调整参数以保证时间一致性（如《战地4》和《星球大战：前线》的视觉效果，图2）。

​1.2 范围与目标​

图3展示了 Frostbite 的目标效果：

  • 支持动态时间的逼真天空
  • 随太阳位置变化的动态光照
  • 大气散射
  • 随天气演变的云层

技术需支持 30/60 FPS 游戏，符合物理框架（参数解耦、物理化参数描述介质属性），并在动态时间/天气下保持系统同步与视觉一致性（如云层增厚影响大气散射、阴影及全局光照）。

​1.3 贡献者​

感谢 Frostbite 团队、学生及游戏团队工程师/艺术家的合作：

  • 天空与大气系统：Gustav Bodare、Edvard Sandberg（硕士生）、BioWare、DICE、Ghost
  • 体积云系统：Rurik Hogfeldt（硕士生）、BioWare 团队
  • 特别致谢：Per Einarsson、Charles de Rousiers 等 Frostbite 渲染团队成员，以及 Fabrice Neyret、Eric Bruneton 的研究支持。

​2 参与介质​

参与介质指含微粒（如尘埃、水滴、分子）的体积。其与光的交互由散射描述，密度分布决定形态（如均匀雾为均质介质，云为异质介质）。

​2.1 单次散射​

介质中光的传输事件包括：

  • 吸收（σₐ）​：光子被介质吸收
  • 外散射（σₛ）​：光子被粒子散射（由相位函数 p 控制方向）
  • 内散射（σₛ）​：散射光子进入当前路径
  • 发射：本文忽略发光介质

单次散射的亮度积分公式为：
<math xmlns="http://www.w3.org/1998/Math/MathML"> L i ( x i , ω i ) = Tr ⁡ ( x , x s ) L ( x s , ω i ) + ∫ t = 0 S Tr ⁡ ( x , x t ) L s c a t ( x t , ω i ) σ s d t ( 1 ) L_i\left(x_i,\omega_i\right)=\operatorname{Tr}\left(x, x_s\right) L\left(x_s,\omega_i\right)+\int_{t=0}^S\operatorname{Tr}\left(x, x_t\right) L s c a t\left(x_t,\omega_i\right)\sigma_s d t \quad (1) </math>Li(xi,ωi)=Tr(x,xs)L(xs,ωi)+∫t=0STr(x,xt)Lscat(xt,ωi)σsdt(1)

​透射率 ​ <math xmlns="http://www.w3.org/1998/Math/MathML"> Tr ⁡ \operatorname{Tr} </math>Tr 由消光系数 σₜ = σₐ + σₛ 决定（图6）：
<math xmlns="http://www.w3.org/1998/Math/MathML"> Tr ⁡ ( x a , x b ) = exp ⁡ ( − ∫ x = x a x b σ t ( x ) d t ) ( 2 ) \operatorname{Tr}\left(x_{a}, x_{b}\right)=\exp\left(-\int_{x=x_{a}}^{x_{b}}\sigma_{t}(x) d t\right) \quad (2) </math>Tr(xa,xb)=exp(−∫x=xaxbσt(x)dt)(2)

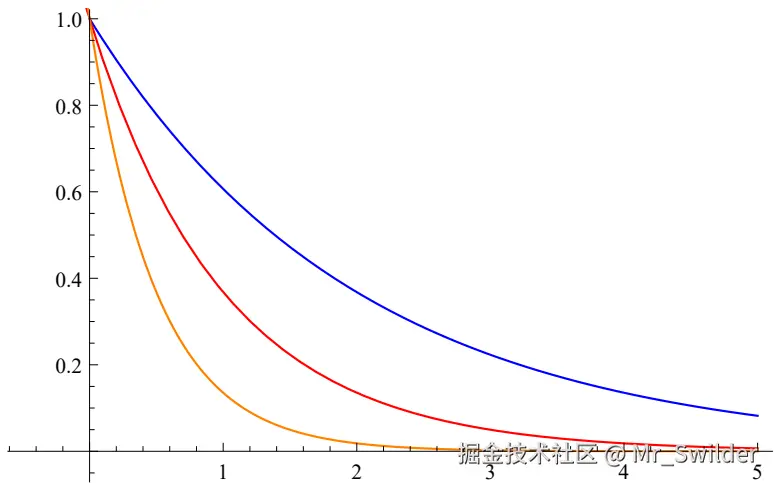
​内散射事件 ​ <math xmlns="http://www.w3.org/1998/Math/MathML"> Lscat ⁡ \operatorname{Lscat} </math>Lscat 计算光源贡献（含相位函数 p 和可见性函数 Vis）：
<math xmlns="http://www.w3.org/1998/Math/MathML"> Lscat ⁡ ( x , ω i ) = ∑ i = 0 lights p ( ω i , L ) Vis ⁡ ( x , L ) L i ( x , L ) ( 3 ) \operatorname{Lscat}\left(x,\omega_i\right)=\sum_{i=0}^{\text{lights}} p\left(\omega_i, L\right)\operatorname{Vis}(x, L) L_{i}(x, L) \quad (3) </math>Lscat(x,ωi)=∑i=0lightsp(ωi,L)Vis(x,L)Li(x,L)(3)

​体积阴影 由介质自遮挡引起，通过光线步进计算：
<math xmlns="http://www.w3.org/1998/Math/MathML"> volumetricShadow ( x , L ) = Tr ⁡ ( x , x L ) ( 4 ) \text{volumetricShadow}(x, L)=\operatorname{Tr}\left(x, x_L\right) \quad (4) </math>volumetricShadow(x,L)=Tr(x,xL)(4)

​2.2 反照率​

反照率 ρ 表示散射与吸收的相对重要性：
<math xmlns="http://www.w3.org/1998/Math/MathML"> ρ = σ s / σ t ( 5 ) \rho=\sigma_s / \sigma_t \quad (5) </math>ρ=σs/σt(5)

  • ρ≈0：介质黑暗（如黑烟）
  • ρ≈1：介质明亮（如空气、云）

​2.3 相位函数​

粒子半径与波长关系（ <math xmlns="http://www.w3.org/1998/Math/MathML"> x = 2 π r / λ x=2\pi r / \lambda </math>x=2πr/λ）决定散射类型：

  • 瑞利散射（x≪1，如大气）
  • 米氏散射（x≈1，如雾）
  • 几何散射（x≫1，如雨滴）

​2.3.1 各向同性散射相位 ​
<math xmlns="http://www.w3.org/1998/Math/MathML"> p ( θ ) = 1 4 π ( 7 ) p(\theta)=\frac{1}{4\pi} \quad (7) </math>p(θ)=4π1(7)

​2.3.2 瑞利散射相位 ​
<math xmlns="http://www.w3.org/1998/Math/MathML"> p ( θ ) = 3 16 π ( 1 + cos ⁡ 2 θ ) ( 8 ) p(\theta)=\frac{3}{16\pi}\left(1+\cos^{2}\theta\right) \quad (8) </math>p(θ)=16π3(1+cos2θ)(8)

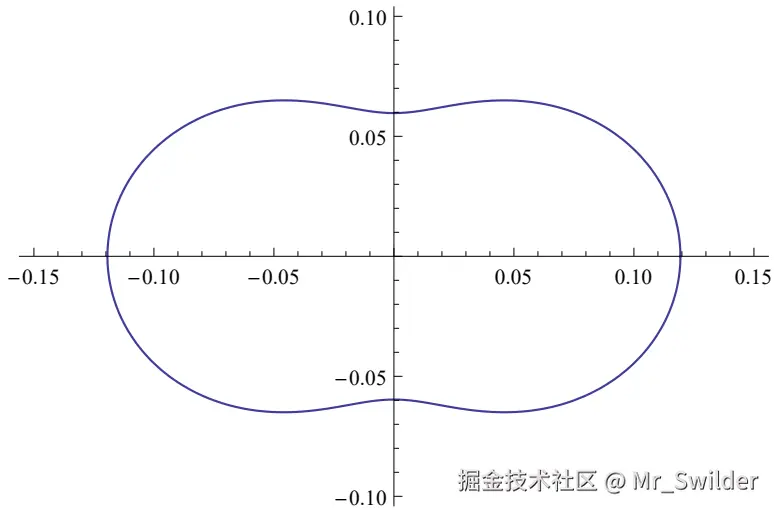
​2.3.3 米氏散射相位 ​

Henyey-Greenstein 相位函数（g∈(-1,1) 控制前/后向散射）：
<math xmlns="http://www.w3.org/1998/Math/MathML"> p h g ( θ , g ) = 1 − g 2 4 π ( 1 + g 2 − 2 g cos ⁡ θ ) 1.5 ( 9 ) p_{hg}(\theta, g)=\frac{1-g^2}{4\pi\left(1+g^2-2g\cos\theta\right)^{1.5}} \quad (9) </math>phg(θ,g)=4π(1+g2−2gcosθ)1.51−g2(9)

​Schlick 近似 ​（高效替代方案）：
<math xmlns="http://www.w3.org/1998/Math/MathML"> p ( θ , k ) = 1 − k 2 4 π ( 1 + k cos ⁡ θ ) 2 , k ≈ 1.55 g − 0.55 g 3 ( 10 ) p(\theta, k)=\frac{1-k^2}{4\pi(1+k\cos\theta)^2}, \quad k\approx1.55g-0.55g^3 \quad (10) </math>p(θ,k)=4π(1+kcosθ)21−k2,k≈1.55g−0.55g3(10)

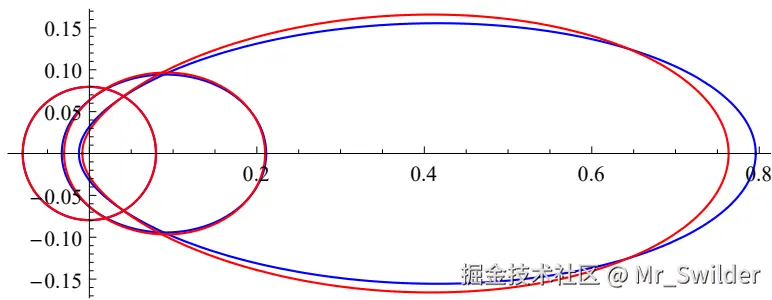
​2.3.4 几何散射相位 ​

复杂相位函数（如彩虹）可通过 MiePlot 生成（图10）。

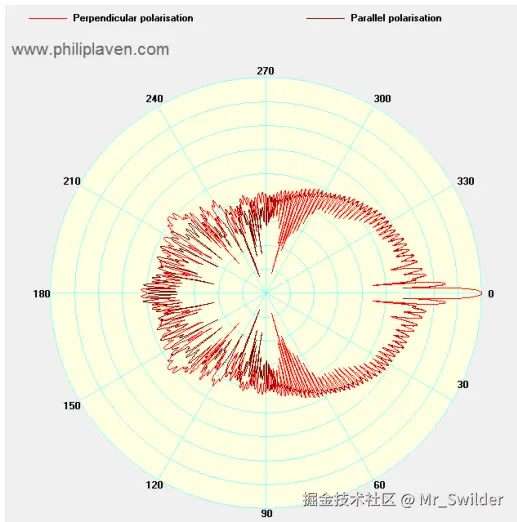
​2.4 示例​

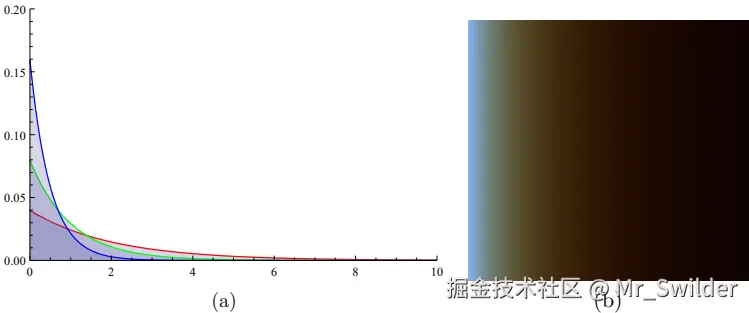
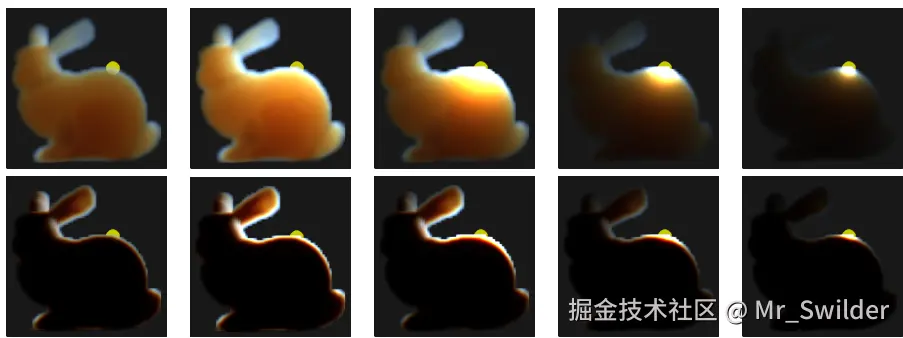
图11-14 展示参数对体积渲染的影响：

  • 图11：散射与体积阴影的视觉贡献
  • 图12：均匀介质中的光散射梯度
  • 图13：密度变化对斯坦福兔/龙模型的影响
  • 图14：Henyey-Greenstein 相位函数 g 值变化效果

​3 天空与大气​

本节基于 Bruneton[BN08]、Elek[Ele09]、Yusov[Yus13a] 的研究实现高效实时渲染。

​3.1 先前工作​

​天空渲染模型分类​：

  • 解析模型（如 Preetham99[PSS99]）：依赖浑浊度等参数，灵活性有限
  • 迭代模型（如 Bruneton08[BN08]）：通过光线步进生成查找表（LUT）

Frostbite 选择 ​3D LUT 方案​[Ele09]，牺牲方位角依赖性（忽略地球阴影）以提升性能，并采用 Yusov 参数化减少地平线伪影。

​3.2 天空与大气参与介质​

大气散射核心要素：

  • 瑞利散射：分子级散射（蓝光散射最强），主导白昼蓝天
  • 米氏散射：大粒子散射（与波长无关），产生日晕效应

​3.3 大气成分​

​表2：地球大气默认属性​

类型 散射系数 σₛ (m⁻¹) 消光系数 σₜ (m⁻¹) 分布
瑞利（分子） (5.8e⁻⁶, 1.35e⁻⁵, 3.31e⁻⁵) σₛᴿᵃʸ e−h/8.0kme^{-h/8.0 \text{km}}e−h/8.0km
米氏（尘埃） ≥2e⁻⁶ 1.11×σₛᴹⁱᵉ e−h/1.2kme^{-h/1.2 \text{km}}e−h/1.2km
臭氧 0 σₐᴼ³ e−h/8.0kme^{-h/8.0 \text{km}}e−h/8.0km

瑞利系数沿用文献值，米氏系数随大气状态（污染、沙尘等）变化（图15）。

​3.4 臭氧吸收​

臭氧吸收系数 σₐᴼ³ 由分子密度与截面计算得出（详见表注），其效果见图16。未考虑臭氧时天空偏黄，加入后黄昏/黎明色调更自然。

​3.5 我们的方法​

​关键技术选择​：

  1. 3D 散射 LUT 替代 4D 方案
  2. 低分辨率（32×32×16）大气透视体积纹理加速雾效计算
  3. 高度雾颜色取自 LUT 地平线值
  4. LUT 更新成本通过多帧分摊（表3）

​表3：Xbox One 天空渲染性能​

渲染阶段 耗时
720p 主视图 0.42 ms
大气透视体积（32×32×16） 0.05 ms
LUT 单帧更新 3.50 ms
LUT 19帧分摊更新 0.22 ms/帧

​结果​：

  • 支持外星大气渲染（如火星蓝调日落，图19-20）
  • 应用于《极品飞车》《镜之边缘：催化剂》等游戏

​4 太阳、月亮与星辰​

​4.1 太阳​

​4.1.1 太阳照度 ​

地表太阳照度 Eₛ 为 100,000--120,000 Lux。艺术家通过天顶照度​ Eₛᶻᵉⁿⁱᵗʰ 设置光照强度。

​4.1.2 太阳亮度 ​

亮度 Lₛ 由照度转换：

  1. 计算太阳立体角 ωₛ（物理角直径 0.527°--0.545°）
  2. 地表亮度 <math xmlns="http://www.w3.org/1998/Math/MathML"> L s z e n i t h = E s z e n i t h / ω s L_s^{zenith} = E_s^{zenith} / \omega_s </math>Lszenith=Eszenith/ωs
  3. 外层空间亮度 <math xmlns="http://www.w3.org/1998/Math/MathML"> L s o u t e r = L s z e n i t h / T r a t m o s p h e r e z e n i t h L_s^{outer} = L_s^{zenith} / Tr_{atmosphere}^{zenith} </math>Lsouter=Lszenith/Tratmospherezenith
  4. 渲染时应用大气透射率 <math xmlns="http://www.w3.org/1998/Math/MathML"> L s = T r a t m o s p h e r e × L s o u t e r L_s = Tr_{atmosphere} \times L_s^{outer} </math>Ls=Tratmosphere×Lsouter

透射率随太阳高度变化（图23）：

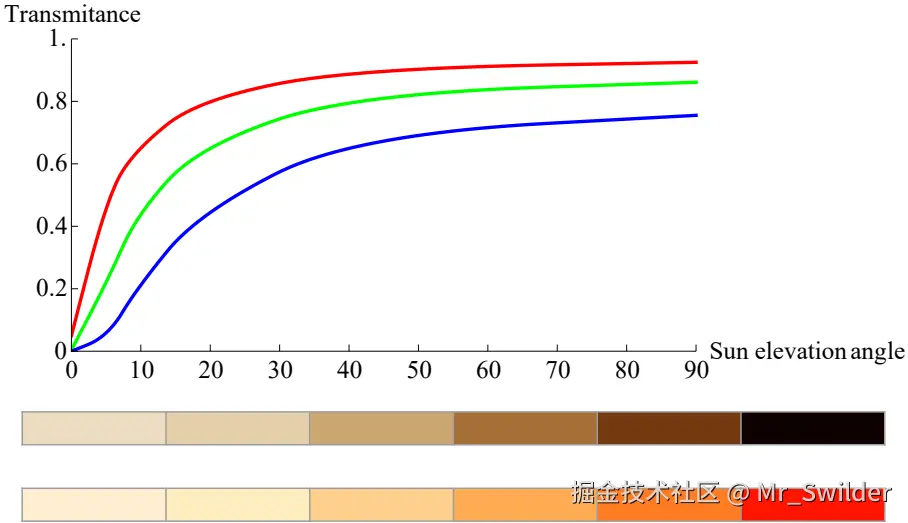
​4.1.3 临边昏暗 ​

太阳盘面亮度分布不均（中心亮于边缘），采用天体物理模型实现（图24）：

​4.2 月亮​

月亮的视觉要点：

  • 角直径：0.488°--0.568°
  • 地表照度：0.26 Lux
  • 亮度计算类似太阳（需考虑反照率纹理）

​4.3 星辰​

星辰贡献照度约 3e⁻² W/m²，渲染时依据温度通过普朗克定律着色。

​4.4 结果​

图26展示黎明/夜晚的天体渲染效果，其反射贡献增强场景一致性。

​5 云​

​5.1 背景与先前工作​

云渲染技术演进：

  • 纹理流动[Gue14]：静态天空贴图+运动模拟
  • 粒子系统[Har02][Yus14]：高效但限于积云形态（图27）
  • 体积混合[Bou+08]：网格+光线步进，电影级质量（图28）
  • 实时体积[Sch15]：噪声建模+时间积分，游戏适用（图29）

Frostbite 采用 Schneider 方案，因其支持：

✅ 逼真云形态 ✅ 大尺度覆盖 ✅ 动态天气 ✅ 体积光照/阴影

​5.2 云参与介质材质​

水云参数[HKS98]：

  • 单次散射反照率 ρ≈1 → σₛ≈σₜ
  • 消光系数：层云 0.04--0.06，积云 0.05--0.12（550nm）

​5.3 云的创作​

​5.3.1 云的分布与密度 ​

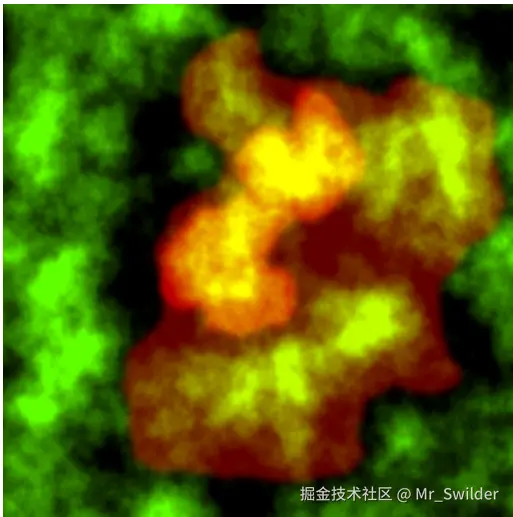
艺术家通过两纹理控制云：

  1. ​天气纹理​（图30）：

    • R 通道：2D 投影云密度
    • G 通道：云类型索引

  2. ​云类型纹理​（图31）：

    • R 通道：高度密度分布
    • G 通道：侵蚀量（湍流强度）

​5.4 云噪声​

噪声纹理生成方案（附录D）：

  • ​噪声L​：Perlin-Worley 噪声（基础形状）

  • ​噪声H​：多频 Worley 噪声（边缘细节）

​5.5 云渲染​

光线步进集成组件（图33）：

  1. 背景透射
  2. 环境光照
  3. 无阴影直射光
  4. 云自阴影直射光
  5. 含相位函数的阴影直射光

​5.5.1 环境光照​

  • 来源：球谐光照探针
  • 优化：垂直梯度权重 + 去饱和度控制

​5.5.2 太阳阴影采样​

  • 沿太阳方向步进采样
  • 渐进式采样 + 抖动实现柔和阴影

​5.5.3 时间散射积分​

  • 每帧随机偏移采样点

  • 指数移动平均混合历史帧

  • 运动时重投影防模糊（图34）

​5.6 改进的散射积分​

​5.6.1 常规积分问题 ​

传统散射积分（代码清单1）因采样顺序导致能量不守恒（图35）：

  • 先散射（S）后透射（T）：能量过高
  • 先透射（T）后散射（S）：能量过低

​5.6.3 能量守恒分析积分 ​

提出新公式（图37）：
<math xmlns="http://www.w3.org/1998/Math/MathML"> ∫ x = 0 d e − σ t x S d x = S ( 1 − e − σ t d ) σ t ( 17 ) \int_{x=0}^{d} e^{-\sigma_t x} S dx = \frac{S(1-e^{-\sigma_t d})}{\sigma_t} \quad (17) </math>∫x=0de−σtxSdx=σtS(1−e−σtd)(17)

​5.7 云相位函数​

​双瓣相位函数 解决单瓣模型缺陷（图39）：
<math xmlns="http://www.w3.org/1998/Math/MathML"> p d u a l ( θ ) = lerp ( p h g ( θ , g 0 ) , p h g ( θ , g 1 ) , w ) ( 18 ) p_{dual}(\theta) = \text{lerp}(p_{hg}(\theta,g_0), p_{hg}(\theta,g_1), w) \quad (18) </math>pdual(θ)=lerp(phg(θ,g0),phg(θ,g1),w)(18)

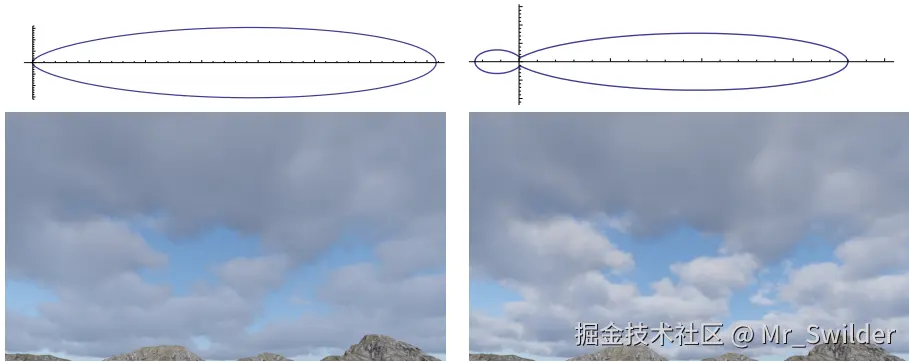
​5.8 多次散射​

采用 Wrenninge 的散射八度迭代法 [WKL13]：
<math xmlns="http://www.w3.org/1998/Math/MathML"> Lmultiscat = ∑ n = 0 N − 1 Lscat n ( 19 ) \text{Lmultiscat} = \sum_{n=0}^{N-1} \text{Lscat}_n \quad (19) </math>Lmultiscat=∑n=0N−1Lscatn(19)

参数缩放需满足 <math xmlns="http://www.w3.org/1998/Math/MathML"> a ≤ b a \leq b </math>a≤b 以保持能量守恒（图40）。

​5.9 其他交互​

​关键交互效果​：

  • 云阴影影响全局光照（Enlighten 系统）

  • 大气透视对云的透射影响（图41中）

  • 云层覆盖对大气透视的影响（图41右）

​5.9.1 大气透视影响云​

  • 计算云层透射加权平均深度（图42）
  • 采样大气透视纹理并应用

​5.9.2 云影响大气透视 ​

透射率与散射光贡献公式：
<math xmlns="http://www.w3.org/1998/Math/MathML"> L A P = L A P × Tr c l o u d + L c l o u d ( 22 ) L_{AP} = L_{AP} \times \text{Tr}{cloud} + L{cloud} \quad (22) </math>LAP=LAP×Trcloud+Lcloud(22)

​5.10 性能​

​表4：Xbox One 云渲染性能​

视图 720p 耗时 1080p 耗时
主视图 0.91 ms 1.60 ms
平面反射视图 0.14 ms 0.20 ms

​5.11 结果​

艺术家实现的云类型复现（图45-50）：

  • 层云（Altostratus，图45）
  • 积云（Cumulus，图46）
  • 积雨云（Cumulonimbus，图49-50）

技术应用于《极品飞车：复仇》（图51）：

​6 结论​

技术已应用于《战地》《FIFA》《质量效应》等系列（图52），核心挑战是高性能 ​（60 FPS）、系统交互 与艺术家工作流的平衡。未来方向包括：大气透视的云阴影优化、云与地形的深度合成、云环境光遮蔽改进等。

​附录（节选）​​

​附录A：天空LUT参数化代码​

c 复制代码 
// 高度标准化  
float normalizedHeight = saturate(height / (atmosphereRadius - earthRadius));  
// 视角天顶角映射  
float normalizedViewZenith = 0.5 * atan(max(cosView, -0.45) * tan(1.26 * 0.75)) / 0.75 + 0.74;

​附录B：太阳临边昏暗模型​

c 复制代码 
// Necas 模型（1996）  
float3 factor = a0 + a1*mu + a2*mu² + a3*mu³ + a4*mu⁴ + a5*mu⁵;  
finalLuminance *= factor;

​附录C：能量守恒散射积分证明​

<math xmlns="http://www.w3.org/1998/Math/MathML"> ∫ 0 d e − σ t x S d x = S σ t ( 1 − e − σ t d ) \int_0^d e^{-\sigma_t x}S dx = \frac{S}{\sigma_t} \left(1 - e^{-\sigma_t d}\right) </math>∫0de−σtxSdx=σtS(1−e−σtd)

​附录D：平铺噪声库​

开源库提供 Perlin-Worley 噪声生成：
GitHub: TileableVolumeNoise

​注​：全文翻译严格遵循原文结构与术语，图片嵌入位置匹配原始上下文。数学公式保留 LaTeX 格式，代码块保留缩进与注释。

相关推荐
F2E_Zhangmo24 分钟前
基于cornerstone3D的dicom影像浏览器 第二章 加载本地文件夹中的dicom文件并归档
前端·javascript·css
用户214118326360241 分钟前
Nano Banana免费方案来了！Docker 一键部署 + 魔搭即开即用，小白也能玩转 AI 图像编辑
前端
Zacks_xdc1 小时前
【前端】使用Vercel部署前端项目，api转发到后端服务器
运维·服务器·前端·安全·react.js
给月亮点灯|1 小时前
Vue基础知识-脚手架开发-使用Axios发送异步请求+代理服务器解决前后端分离项目的跨域问题
前端·javascript·vue.js
张迅之2 小时前
【React】Ant Design 5.x 实现tabs圆角及反圆角效果
前端·react.js·ant-design
蔗理苦3 小时前
2025-09-05 CSS3——盒子模型
前端·css·css3
二川bro4 小时前
第25节：VR基础与WebXR API入门
前端·3d·vr·threejs
上单带刀不带妹4 小时前
Node.js 的模块化规范是什么？CommonJS 和 ES6 模块有什么区别？
前端·node.js·es6·模块化
缘如风4 小时前
easyui 获取自定义的属性
前端·javascript·easyui
诗书画唱4 小时前
【前端教程】JavaScript 实现图片鼠标悬停切换效果与==和=的区别
开发语言·前端·javascript
热门推荐
012025 年高教社杯全国大学生数学建模竞赛C 题 NIPT 的时点选择与胎儿的异常判定 完整成品思路模型代码分享，全网首发高质量！！！022025年数学建模国赛C题超详细解题思路032025全国大学生数学建模C题保姆级思路模型（持续更新）：NIPT 的时点选择与胎儿的异常判定042025高教社杯国赛数学建模选题建议+初步分析052025国赛B题保姆级教程思路分析 碳化硅外延层厚度的确定06UV安装并设置国内源07奈飞工厂官网，国内Netflix影视在线看|中文网页电脑版入口08KGG转MP3工具|非KGM文件|解密音频09（E题｜AI 辅助智能体测）2025年高教杯全国大学生数学建模国赛解题思路|完整代码论文集合10不再让Windows更新！&Edge游戏助手卸载及关闭自动更新