剑指offer-14、链表中倒数第k个结点

题⽬描述

输⼊⼀个链表，输出该链表中倒数第k个结点。

例如输⼊{1,2,3,4,5} , 2 时，对应的链表结构如下图所示：

其中蓝⾊部分为该链表的最后2 个结点，所以返回倒数第2 个结点（也即结点值为4 的结点）即可，系统会打印后⾯所有的节点来⽐较。

示例1 输⼊：{1,2,3,4,5},2 返回值：{4,5} 说明：返回倒数第2个节点4，系统会打印后⾯所有的节点来⽐较。

示例2 输⼊：{2},8 返回值：{}

思路及解答

两次遍历法

第一次遍历计算链表长度n
第二次遍历到第n-K+1个节点（即倒数第K个节点）
如果K大于链表长度，返回null

java 复制代码

public ListNode findKthToTail(ListNode head, int k) {
    if (head == null || k <= 0) return null;
    
    // 第一次遍历计算链表长度
    int length = 0;
    ListNode current = head;
    while (current != null) {
        length++;
        current = current.next;
    }
    
    // 检查k是否有效
    if (k > length) return null;
    
    // 第二次遍历找到目标节点
    current = head;
    for (int i = 0; i < length - k; i++) {
        current = current.next;
    }
    
    return current;
}

时间复杂度：O(n)，需要遍历链表两次
空间复杂度：O(1)，只使用了固定数量的指针

双指针法（推荐）

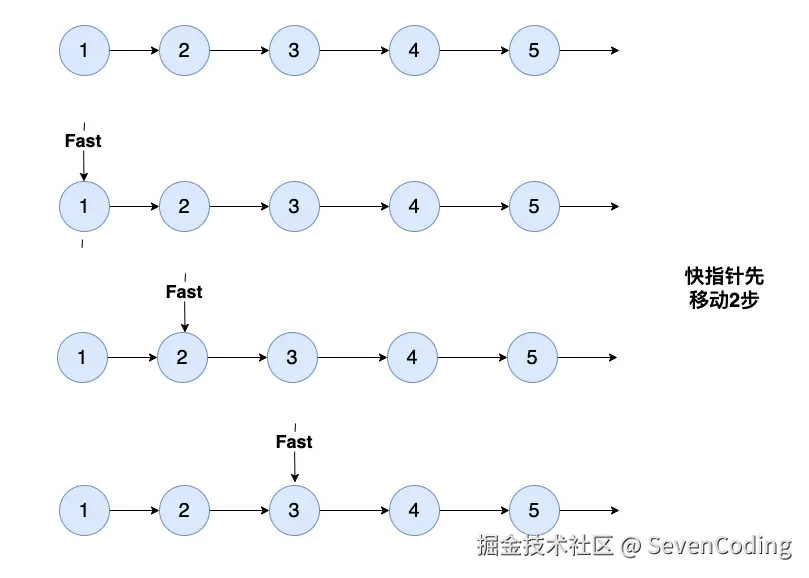
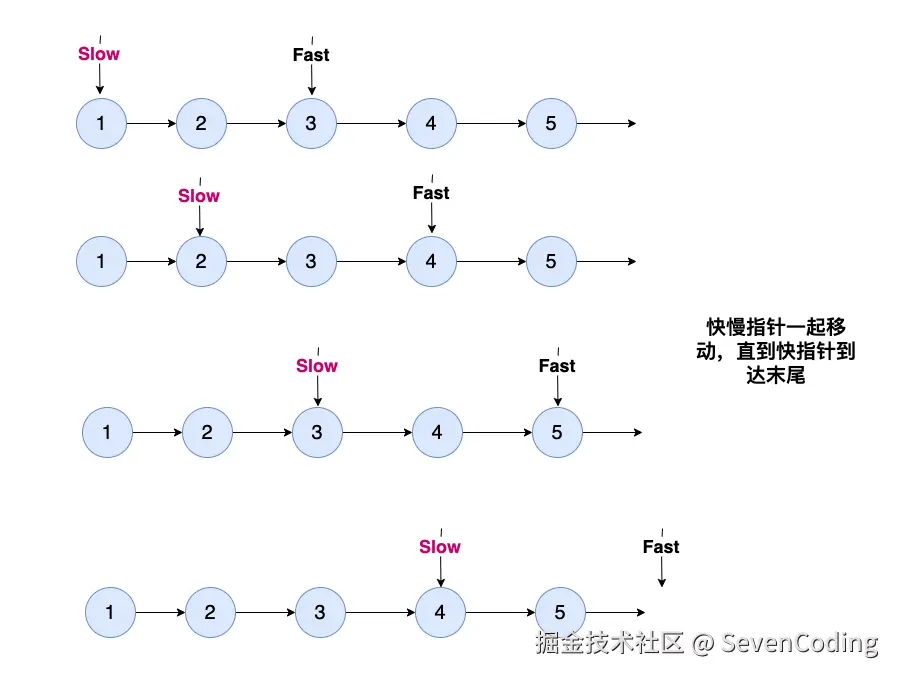
快慢双指针，先让第1 个指针先⾛k 步，然后第2 个指针开始⾛，⽽且两个指针⼀起⾛，直到第⼀个指针⾛到最后的位置。

使用快慢两个指针，快指针先移动K步
然后两个指针同步移动，当快指针到达末尾时，慢指针正好指向倒数第K个节点
如果快指针在移动K步前到达末尾，说明K大于链表长度

java 复制代码

public ListNode findKthToTail(ListNode head, int k) {
    if (head == null || k <= 0) return null;
    
    ListNode fast = head;
    ListNode slow = head;
    
    // 快指针先移动k步
    for (int i = 0; i < k; i++) {
        if (fast == null) return null; // k大于链表长度
        fast = fast.next;
    }
    
    // 同步移动两个指针
    while (fast != null) {
        fast = fast.next;
        slow = slow.next;
    }
    
    return slow;
}

时间复杂度：O(n)，只需遍历链表一次
空间复杂度：O(1)，使用了两个指针

栈辅助法（空间换时间）

将所有节点压入栈
弹出K个节点，最后一个弹出的即为所求
如果栈中节点不足K个，返回null

java 复制代码

public ListNode findKthToTail(ListNode head, int k) {
    if (head == null || k <= 0) return null;
    
    Stack<ListNode> stack = new Stack<>();
    ListNode current = head;
    
    // 所有节点入栈
    while (current != null) {
        stack.push(current);
        current = current.next;
    }
    
    // 检查k是否有效
    if (k > stack.size()) return null;
    
    // 弹出k个节点
    ListNode result = null;
    for (int i = 0; i < k; i++) {
        result = stack.pop();
    }
    
    return result;
}

时间复杂度：O(n)，需要遍历链表两次（入栈和出栈）
空间复杂度：O(n)，需要额外栈空间存储所有节点

递归回溯法

递归遍历到链表末尾
回溯时计数，当计数等于K时返回当前节点
使用全局变量或包装类传递计数

java 复制代码

private int count = 0;

public ListNode findKthToTail(ListNode head, int k) {
    if (head == null) return null;
    
    ListNode node = getKthFromEnd(head.next, k);
    count++;
    
    if (count == k) {
        return head;
    }
    return node;
}

时间复杂度：O(n)，需要完整遍历链表
空间复杂度：O(n)，递归栈空间开销

方法对比与总结

方法	时间复杂度	空间复杂度	优点	缺点
两次遍历法	O(n)	O(1)	实现简单	需要两次遍历
双指针法	O(n)	O(1)	一次遍历，效率高	边界条件需仔细处理
栈辅助法	O(n)	O(n)	实现直观	空间开销大
递归回溯法	O(n)	O(n)	展示递归思想	空间效率低