【机器学习之推荐算法】基于矩阵分解和损失函数梯度下降的协同过滤算法实现

基于矩阵分解的CF算法实现（一）：LFM

LFM也就是前面提到的Funk SVD矩阵分解

LFM原理解析

LFM(latent factor model) 隐语义模型核心思想是通过隐含特征联系用户和物品，如下图：

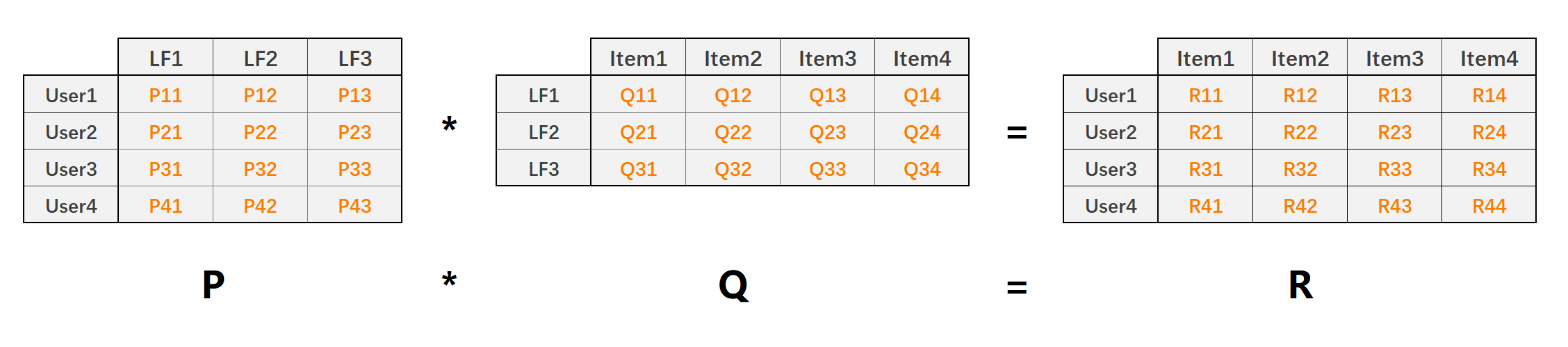
• P矩阵是User-LF矩阵，即用户和隐含特征矩阵。LF有三个，表示总共有三个隐含特征。
• Q矩阵是LF-Item矩阵，即隐含特征和物品的矩阵
• R矩阵是User-Item矩阵，有P*Q得来
• 能处理稀疏评分矩阵

利用矩阵分解技术，将原始User-Item的评分矩阵（稠密/稀疏）分解为P和Q矩阵，然后利用P∗QP*QP∗Q还原出User-Item评分矩阵RRR。整个过程相当于降维处理，其中：

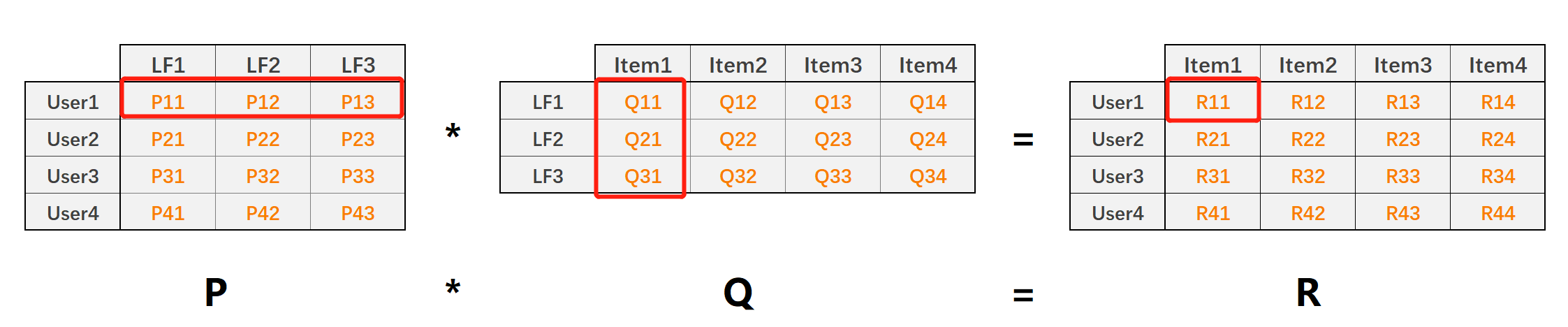
• 矩阵值P11P_{11}P11表示用户1对隐含特征1的权重值

• 矩阵值Q11Q_{11}Q11表示隐含特征1在物品1上的权重值

• 矩阵值R11R_{11}R11就表示预测的用户1对物品1的评分，且R11=P1,k⃗⋅Qk,1⃗R_{11}=\vec{P_{1,k}}\cdot \vec{Q_{k,1}}R11=P1,k ⋅Qk,1

  

利用LFM预测用户对物品的评分，kkk表示隐含特征数量：
r^ui=puk⃗⋅qik⃗=∑k=1kpukqik \begin{split} \hat {r}{ui} &=\vec {p{uk}}\cdot \vec {q_{ik}} \\&={\sum_{k=1}}^k p_{uk}q_{ik} \end{split} r^ui=puk ⋅qik =k=1∑kpukqik

因此最终，我们的目标也就是要求出P矩阵和Q矩阵及其当中的每一个值，然后再对用户-物品的评分进行预测。

损失函数

同样对于评分预测我们利用平方差来构建损失函数：
Cost=∑u,i∈R(rui−r^ui)2=∑u,i∈R(rui−∑k=1kpukqik)2 \begin{split} Cost &= \sum_{u,i\in R} (r_{ui}-\hat{r}{ui})^2 \\&=\sum{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})^2 \end{split} Cost=u,i∈R∑(rui−r^ui)2=u,i∈R∑(rui−k=1∑kpukqik)2

加入L2正则化：
Cost=∑u,i∈R(rui−∑k=1kpukqik)2+λ(∑Upuk2+∑Iqik2) Cost = \sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})^2 + \lambda(\sum_U{p_{uk}}^2+\sum_I{q_{ik}}^2) Cost=u,i∈R∑(rui−k=1∑kpukqik)2+λ(U∑puk2+I∑qik2)

对损失函数求偏导：
∂∂pukCost=∂∂puk[∑u,i∈R(rui−∑k=1kpukqik)2+λ(∑Upuk2+∑Iqik2)]=2∑u,i∈R(rui−∑k=1kpukqik)(−qik)+2λpuk∂∂qikCost=∂∂qik[∑u,i∈R(rui−∑k=1kpukqik)2+λ(∑Upuk2+∑Iqik2)]=2∑u,i∈R(rui−∑k=1kpukqik)(−puk)+2λqik \begin{split} \cfrac {\partial}{\partial p_{uk}}Cost &= \cfrac {\partial}{\partial p_{uk}}[\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})^2 + \lambda(\sum_U{p_{uk}}^2+\sum_I{q_{ik}}^2)] \\&=2\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})(-q_{ik}) + 2\lambda p_{uk} \\\\ \cfrac {\partial}{\partial q_{ik}}Cost &= \cfrac {\partial}{\partial q_{ik}}[\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})^2 + \lambda(\sum_U{p_{uk}}^2+\sum_I{q_{ik}}^2)] \\&=2\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})(-p_{uk}) + 2\lambda q_{ik} \end{split} ∂puk∂Cost∂qik∂Cost=∂puk∂[u,i∈R∑(rui−k=1∑kpukqik)2+λ(U∑puk2+I∑qik2)]=2u,i∈R∑(rui−k=1∑kpukqik)(−qik)+2λpuk=∂qik∂[u,i∈R∑(rui−k=1∑kpukqik)2+λ(U∑puk2+I∑qik2)]=2u,i∈R∑(rui−k=1∑kpukqik)(−puk)+2λqik

随机梯度下降法优化

梯度下降更新参数pukp_{uk}puk：
puk:=puk−α∂∂pukCost:=puk−α[2∑u,i∈R(rui−∑k=1kpukqik)(−qik)+2λpuk]:=puk+α[∑u,i∈R(rui−∑k=1kpukqik)qik−λpuk] \begin{split} p_{uk}&:=p_{uk} - \alpha\cfrac {\partial}{\partial p_{uk}}Cost \\&:=p_{uk}-\alpha [2\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})(-q_{ik}) + 2\lambda p_{uk}] \\&:=p_{uk}+\alpha [\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})q_{ik} - \lambda p_{uk}] \end{split} puk:=puk−α∂puk∂Cost:=puk−α[2u,i∈R∑(rui−k=1∑kpukqik)(−qik)+2λpuk]:=puk+α[u,i∈R∑(rui−k=1∑kpukqik)qik−λpuk]

同理：
qik:=qik+α[∑u,i∈R(rui−∑k=1kpukqik)puk−λqik] \begin{split} q_{ik}&:=q_{ik} + \alpha[\sum_{u,i\in R} (r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})p_{uk} - \lambda q_{ik}] \end{split} qik:=qik+α[u,i∈R∑(rui−k=1∑kpukqik)puk−λqik]
随机梯度下降： 向量乘法 每一个分量相乘 求和
puk:=puk+α[(rui−∑k=1kpukqik)qik−λ1puk]qik:=qik+α[(rui−∑k=1kpukqik)puk−λ2qik] \begin{split} &p_{uk}:=p_{uk}+\alpha [(r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})q_{ik} - \lambda_1 p_{uk}] \\&q_{ik}:=q_{ik} + \alpha[(r_{ui}-{\sum_{k=1}}^k p_{uk}q_{ik})p_{uk} - \lambda_2 q_{ik}] \end{split} puk:=puk+α[(rui−k=1∑kpukqik)qik−λ1puk]qik:=qik+α[(rui−k=1∑kpukqik)puk−λ2qik]

由于P矩阵和Q矩阵是两个不同的矩阵，通常分别采取不同的正则参数，如λ1\lambda_1λ1和λ2\lambda_2λ2

算法实现

'''
LFM Model
'''
import pandas as pd
import numpy as np

# 评分预测    1-5
class LFM(object):

    def __init__(self, alpha, reg_p, reg_q, number_LatentFactors=10, number_epochs=10, columns=["uid", "iid", "rating"]):
        self.alpha = alpha # 学习率
        self.reg_p = reg_p    # P矩阵正则
        self.reg_q = reg_q    # Q矩阵正则
        self.number_LatentFactors = number_LatentFactors  # 隐式类别数量
        self.number_epochs = number_epochs    # 最大迭代次数
        self.columns = columns
    
    #数据预处理和模型训练
    def fit(self, dataset):
        '''
        fit dataset
        :param dataset: uid, iid, rating
        :return:
        '''
       # 转换为 DataFrame：
        self.dataset = pd.DataFrame(dataset)

        '''
        ① 对 dataset 进行操作。dataset 是一个 Pandas DataFrame，它包含了用户ID（userId）、
        物品ID（movieId）和评分（rating）.
        ② 对数据集dataset按照self.columns[0]进行分组，分组后，每个分组代表一个用户的数据。
        ③ 分组后对数据进行agg聚合操作，list 表示将每个分组中的元素转换为列表。具体来说，self.columns[1] 和 
        self.columns[2]    分别是 movieId 和 rating，这意味着对于每个用户（userId），
        我们将会把该用户评分的所有 movieId 和相应的 rating 收集到一个列表中.
        ④ 最终结果是：对每个用户（userId）,movieId和rating的列表将作为该用户的评分数据。
            userId        movieId       rating
            1001         [1, 2, 3]    [4.0, 5.0, 3.5]
        '''
     #构建用户评分记录和物品评分记录  
        # 用户评分
        self.users_ratings = dataset.groupby(self.columns[0]).agg([list])[[self.columns[1], self.columns[2]]]
         # 物品评分
        self.items_ratings = dataset.groupby(self.columns[1]).agg([list])[[self.columns[0], self.columns[2]]]
        #计算全局平均评分（用于处理冷启动，即用户或物品不在训练集中时的预测）
        self.globalMean = self.dataset[self.columns[2]].mean()
        #调用梯度下降函数，训练矩阵分解模型
        self.P, self.Q = self.sgd()
        
    #初始化隐向量矩阵
    def _init_matrix(self):
        '''
        初始化P和Q矩阵，同时为设置0，1之间的随机值作为初始值
        :return:
        '''
        # User-LF
        # 每个用户一个长度为 number_LatentFactors 的向量
        P = dict(zip(
            self.users_ratings.index,
            np.random.rand(len(self.users_ratings), self.number_LatentFactors).astype(np.float32)
        ))
        # Item-LF
        # 每个物品一个长度为 number_LatentFactors 的向量
        Q = dict(zip(
            self.items_ratings.index,
            np.random.rand(len(self.items_ratings), self.number_LatentFactors).astype(np.float32)
        ))
        return P, Q
    
    #随机梯度下降训练函数
    def sgd(self):
        '''
        使用随机梯度下降，优化结果
        :return:
        '''
        #初始化P、Q矩阵
        P, Q = self._init_matrix()

        for i in range(self.number_epochs):
            print("iter%d"%i)
            error_list = []
            for uid, iid, r_ui in self.dataset.itertuples(index=False):
                # User-LF P
                ## Item-LF Q
               
                v_pu = P[uid] #当前用户向量
                v_qi = Q[iid] #物品向量
                # 损失函数
                err = np.float32(r_ui - np.dot(v_pu, v_qi))
                
                #梯度下降更新参数p_uk
                v_pu += self.alpha * (err * v_qi - self.reg_p * v_pu)
                #梯度下降更新参数p_ik
                v_qi += self.alpha * (err * v_pu - self.reg_q * v_qi)
                
                P[uid] = v_pu 
                Q[iid] = v_qi

                # for k in range(self.number_of_LatentFactors):
                #     v_pu[k] += self.alpha*(err*v_qi[k] - self.reg_p*v_pu[k])
                #     v_qi[k] += self.alpha*(err*v_pu[k] - self.reg_q*v_qi[k])

                error_list.append(err ** 2)
            print(np.sqrt(np.mean(error_list)))
        return P, Q

    def predict(self, uid, iid):
        # 如果uid或iid不在，我们使用全剧平均分作为预测结果返回
        if uid not in self.users_ratings.index or iid not in self.items_ratings.index:
            return self.globalMean

        p_u = self.P[uid]
        q_i = self.Q[iid]

        return np.dot(p_u, q_i)

    def test(self,testset):
        '''预测测试集数据'''
        for uid, iid, real_rating in testset.itertuples(index=False):
            try:
                pred_rating = self.predict(uid, iid)
            except Exception as e:
                print(e)
            else:
                #对测试集中的每条样本 (uid, iid, rating) 预测评分：
                yield uid, iid, real_rating, pred_rating

if __name__ == '__main__':
    dtype = [("userId", np.int32), ("movieId", np.int32), ("rating", np.float32)]
    dataset = pd.read_csv("datasets/ml-latest-small/ratings.csv", usecols=range(3), dtype=dict(dtype))

    lfm = LFM(0.02, 0.01, 0.01, 10, 100, ["userId", "movieId", "rating"])
    lfm.fit(dataset)
    #进入交互式预测
    while True:
        uid = input("uid: ")
        iid = input("iid: ")
        print(lfm.predict(int(uid), int(iid)))

---

你这段代码是一个经典的 基于矩阵分解（Matrix Factorization, MF） 的 协同过滤推荐系统 ，主要使用了 随机梯度下降（SGD） 来优化模型参数。

下面我会逐模块解释代码逻辑，并且补充清晰注释，帮助你深入理解每个部分。

---

LFM算法解读

🔧 类初始化：__init__

def __init__(self, alpha, reg_p, reg_q, number_LatentFactors=10, number_epochs=10, columns=["uid", "iid", "rating"]):

• alpha: 学习率（控制步长）
• reg_p, reg_q: 分别是用户矩阵P和物品矩阵Q的正则化系数，用于防止过拟合
• number_LatentFactors: 隐向量维度（Latent Factors 的数量），即将用户/物品特征压缩到的低维空间大小
• number_epochs: 最大迭代次数
• columns: 指定输入数据中用户、物品、评分的列名

---

📊 数据预处理和模型训练：fit

def fit(self, dataset):

1. 转换为 DataFrame：

self.dataset = pd.DataFrame(dataset)

1. 构建用户评分记录和物品评分记录：

self.users_ratings = dataset.groupby(self.columns[0]).agg([list])[[self.columns[1], self.columns[2]]]
self.items_ratings = dataset.groupby(self.columns[1]).agg([list])[[self.columns[0], self.columns[2]]]

例如：

userId:    movieId: [1, 2, 3], rating: [4.0, 3.5, 5.0]

这两行代码是为了获取所有用户和所有物品的评分记录（用于初始化 P/Q 矩阵）。

1. 计算全局平均评分（用于处理冷启动，即用户或物品不在训练集中时的预测）：

self.globalMean = self.dataset[self.columns[2]].mean()

1. 训练矩阵分解模型（SGD）：

self.P, self.Q = self.sgd()

---

🧮 初始化隐向量矩阵：_init_matrix

def _init_matrix(self):

• 用户矩阵 P：每个用户一个长度为 number_LatentFactors 的向量
• 物品矩阵 Q：每个物品一个长度为 number_LatentFactors 的向量

P = dict(zip(self.users_ratings.index, np.random.rand(len(self.users_ratings), self.number_LatentFactors)))
Q = dict(zip(self.items_ratings.index, np.random.rand(len(self.items_ratings), self.number_LatentFactors)))

向量初始化为 [0, 1) 之间的随机数。

---

🔁 随机梯度下降训练：sgd

def sgd(self):

核心部分：通过最小化均方误差（MSE）损失函数，更新 P 和 Q。

损失函数目标：

L=∑(u,i)∈R(rui−r^ui)2+λp∥Pu∥2+λq∥Qi∥2 L = \sum_{(u, i) \in R} (r_{ui} - \hat{r}_{ui})^2 + \lambda_p \|P_u\|^2 + \lambda_q \|Q_i\|^2 L=(u,i)∈R∑(rui−r^ui)2+λp∥Pu∥2+λq∥Qi∥2

每一轮迭代步骤如下：

for uid, iid, r_ui in self.dataset.itertuples(index=False):

• v_pu = P[uid]: 当前用户向量
• v_qi = Q[iid]: 当前物品向量

预测评分：

err = r_ui - np.dot(v_pu, v_qi)

err = r_ui - np.dot(v_pu, v_qi) 这行代码是 计算预测误差 ，并且 np.dot() 计算的是两个向量的 内积 。

下面详细解释一下这部分代码。

---

1. np.dot() 是什么？

np.dot() 是 NumPy 库中的函数，用于计算两个向量的 点积（内积）。它的具体含义是：

dot product=∑i=1nai⋅bi \text{dot product} = \sum_{i=1}^{n} a_i \cdot b_i dot product=i=1∑nai⋅bi

假设有两个向量 a=[a1,a2,...,an]\mathbf{a} = [a_1, a_2, \dots, a_n]a=[a1,a2,...,an] 和 b=[b1,b2,...,bn]\mathbf{b} = [b_1, b_2, \dots, b_n]b=[b1,b2,...,bn]，则它们的点积（内积）是：

a⋅b=a1b1+a2b2+⋯+anbn \mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + \dots + a_n b_n a⋅b=a1b1+a2b2+⋯+anbn

对于模型来说，v_pu 和 v_qi 分别是用户 uuu 和物品 iii 的隐向量表示。

• v_pu 是用户 uuu 的隐向量，表示该用户在 number_LatentFactors 个隐特征上的表示。
• v_qi 是物品 iii 的隐向量，表示该物品在 number_LatentFactors 个隐特征上的表示。

通过 内积 ，我们可以得到用户 uuu 对物品 iii 的 预测评分。预测评分的公式就是：

r^ui=pu⋅qi \hat{r}_{ui} = \mathbf{p_u} \cdot \mathbf{q_i} r^ui=pu⋅qi

所以：

np.dot(v_pu, v_qi)

就是计算出用户 uuu 对物品 iii 的预测评分。

2. 误差 err = r_ui - np.dot(v_pu, v_qi)

在实际应用中，r_ui 是用户 uuu 给物品 iii 的实际评分，而 np.dot(v_pu, v_qi) 是模型预测的评分。

因此，err 就是实际评分和预测评分之间的差值，也就是 残差（residual），即：

err=rui−r^ui \text{err} = r_{ui} - \hat{r}_{ui} err=rui−r^ui

这个 残差 会被用来更新隐向量 pu\mathbf{p_u}pu 和 qi\mathbf{q_i}qi，从而使得模型逐步减小预测误差。

3. RMSE (Root Mean Squared Error)

RMSE（均方根误差）是评估推荐系统性能的一个常用指标，它衡量了预测评分与实际评分之间的差异。其公式为：

RMSE=1N∑i=1N(rui−r^ui)2 \text{RMSE} = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (r_{ui} - \hat{r}_{ui})^2} RMSE=N1i=1∑N(rui−r^ui)2

• ruir_{ui}rui 是实际评分
• r^ui\hat{r}_{ui}r^ui 是预测评分
• NNN 是测试集中的样本数

RMSE 是 均方误差（MSE） 的平方根，旨在将预测误差的度量还原到与原始评分相同的单位。它越小，模型的预测精度越高。

4. 在代码中的实现

在代码中，你会看到如下部分：

error_list.append(err ** 2)
print(np.sqrt(np.mean(error_list)))

这里 error_list 是一个列表，用于记录每个样本的误差的平方（也就是 MSE 的一部分）。

• err ** 2 计算的是当前样本的平方误差（即 MSE 的分子部分）。
• np.mean(error_list) 计算所有样本的均方误差（MSE），就是将所有平方误差取平均。
• np.sqrt(np.mean(error_list)) 是取均方误差的平方根，得到 RMSE。

这样做的效果是每经过一轮迭代，都会输出当前模型在训练集上的 RMSE，用来评估模型的收敛程度和训练效果。

---

5. 具体代码解释

error_list.append(err ** 2)

这一行将 每一条样本的平方误差 添加到 error_list 列表中。这是计算 RMSE 的步骤之一。

np.sqrt(np.mean(error_list))

这个部分将所有样本的 平方误差 取平均（得到 MSE），然后再 开根号 ，得到最终的 RMSE。在每一轮的训练中，RMSE 用于衡量模型在训练数据上的误差。

---

6. 总结

• np.dot(v_pu, v_qi) 计算的是用户和物品隐向量的 内积 ，即 预测评分。
• err = r_ui - np.dot(v_pu, v_qi) 是 预测误差（残差），用来衡量模型的预测与实际评分之间的差距。
• RMSE 是 均方根误差，用于衡量模型的预测准确性，公式为：

RMSE=1N∑i=1N(rui−r^ui)2 \text{RMSE} = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (r_{ui} - \hat{r}_{ui})^2} RMSE=N1i=1∑N(rui−r^ui)2

在代码中，RMSE 的实现是通过计算每个样本的平方误差，取均值后开根号来完成的。

🔮 评分预测：predict

def predict(self, uid, iid):

如果用户或物品不在训练集中，用全局平均评分作为预测：

if uid not in self.users_ratings.index or iid not in self.items_ratings.index:
    return self.globalMean

否则返回预测评分：

return np.dot(self.P[uid], self.Q[iid])

---

✅ 测试集预测：test

def test(self, testset):

对测试集中的每条样本 (uid, iid, rating) 预测评分：

yield uid, iid, real_rating, pred_rating

---

🧪 主函数入口（测试）

if __name__ == '__main__':

1. 从 ratings.csv 读取数据（只取前三列）：

dataset = pd.read_csv("datasets/ml-latest-small/ratings.csv", usecols=range(3), dtype=dict(dtype))

1. 实例化模型并训练：

lfm = LFM(0.02, 0.01, 0.01, 10, 100, ["userId", "movieId", "rating"])
lfm.fit(dataset)

1. 进入交互式预测：

while True:
    uid = input("uid: ")
    iid = input("iid: ")
    print(lfm.predict(int(uid), int(iid)))

---

🔍 总结重点：

模块	作用
P, Q 矩阵	用户和物品的低维向量表示
sgd()	通过最小化损失函数优化向量
predict()	用内积预测评分
globalMean	处理冷启动的回退策略
fit()	数据预处理 + 模型训练入口
test()	在测试集上做预测评估

---