文章目录
- [LeetCode 112: 路径总和](#LeetCode 112: 路径总和)
-
- [一、 题目描述](#一、 题目描述)
- [二、 核心思路与解法分析](#二、 核心思路与解法分析)
- 参考解法
- [LeetCode 257: 二叉树的所有路径](#LeetCode 257: 二叉树的所有路径)
-
- [一、 题目描述](#一、 题目描述)
- [二、 核心思路与解法分析](#二、 核心思路与解法分析)
- 参考解法 (标准回溯解法)
- 拓展
- [三、 核心对比与总结](#三、 核心对比与总结)
二叉树路径问题 : LeetCode 112 (路径总和) 【难度:简单;通过率:55.5%】和 LeetCode 257 (二叉树的所有路径)【难度:简单;通过率:71.7%】
这两道题都围绕"从根到叶子的路径"展开,是理解 DFS、回溯思想以及递归参数设计的绝佳案例
LeetCode 112: 路径总和
一、 题目描述
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于 targetSum。如果存在,返回 true;否则,返回 false
示例:
示例 1:
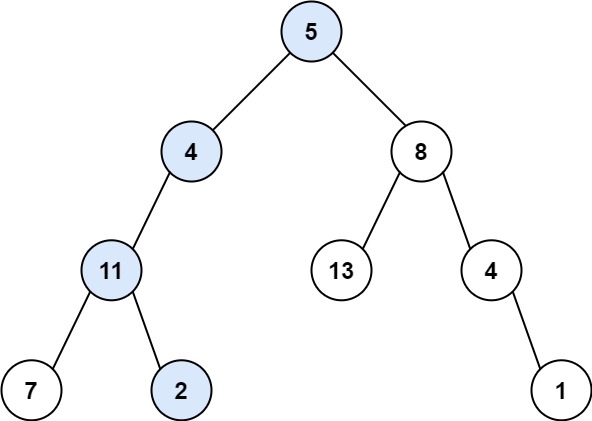
输入: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出: true
解释: 存在路径 5 -> 4 -> 11 -> 2,其和为 22
示例 2:
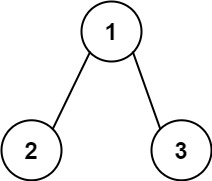
输入: root = [1,2,3], targetSum = 5
输出: false
二、 核心思路与解法分析
目标: 寻找是否存在一条满足条件的路径
思路: 采用深度优先搜索(DFS)。我们从根节点出发,每往下走一步,就将当前路径和累加。当到达一个叶子节点时,检查当前路径和是否等于 targetSum
参考解法
【一种直观的参考代码】:
java
public class Solution {
int target;
boolean isExist = false; // 找到了
// 分而治之 + 递归 + 回溯
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) {
return false;
}
target = targetSum;
// 开启dfs
dfs(0, root);
return isExist;
}
public void dfs(int curSum, TreeNode curNode) {
// 先校验基准情况 (结尾必须是叶子节点)
if ((curSum + curNode.val == target || isExist) && isLeaf(curNode)) {
isExist = true;
return;
}
// 向左子树搜索
if (curNode.left != null) {
dfs(curSum + curNode.val, curNode.left);
}
// 向右子树搜索
if (curNode.right != null) {
dfs(curSum + curNode.val, curNode.right);
}
}
public boolean isLeaf(TreeNode node) {
return node.left == null && node.right == null;
}
}关键点解析:
- 隐式回溯 :
sum是int类型,按值传递。dfs调用返回后,当前栈帧的sum值不变,天然地完成了"回溯" - 剪枝 :
isExist的判断非常关键。一旦找到一条路径,后续的所有递归分支都可以被跳过,大大提高了效率
LeetCode 257: 二叉树的所有路径
一、 题目描述
给你一个二叉树的根节点 root,按 任意顺序 返回所有从根节点到叶子节点的路径
示例:
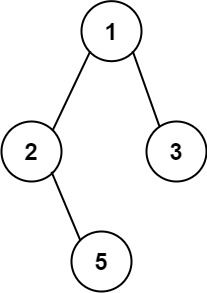
输入: root = [1,2,3,null,5]
输出: ["1->2->5", "1->3"]
二、 核心思路与解法分析
目标: 寻找并记录所有满足条件的路径
思路: 同样采用深度优先搜索(DFS)。但这次我们不仅要累加和,还要记录下路径本身。当到达叶子节点时,将记录好的路径格式化为字符串并存入结果列表
参考解法 (标准回溯解法)
由于需要记录路径,我们必须在递归时维护一个路径列表,并在回溯时手动将其恢复原状(最终再记录结果)
java
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> result = new ArrayList<>();
if (root == null) {
return result;
}
List<Integer> path = new ArrayList<>();
dfs(root, path, result);
return result;
}
/**
* 深度优先搜索
* @param node 当前节点
* @param path 记录从根到当前节点的路径节点值
* @param result 存储最终结果
*/
public void dfs(TreeNode node, List<Integer> path, List<String> result) {
// 1. 将当前节点加入路径
path.add(node.val);
// 2. 判断是否到达叶子节点
if (node.left == null && node.right == null) {
// 到达叶子节点,构建路径字符串并加入结果集
StringBuilder sb = new StringBuilder();
for (int i = 0; i < path.size() - 1; i++) {
sb.append(path.get(i)).append("->");
}
sb.append(path.get(path.size() - 1));
result.add(sb.toString());
// 注意:这里不能直接 return,因为后面还有回溯操作
}
// 3. 递归探索子节点
if (node.left != null) {
dfs(node.left, path, result);
}
if (node.right != null) {
dfs(node.right, path, result);
}
// 4. 显式回溯:
// 离开当前节点前,将它从路径中移除,以便其他分支使用干净的 path
path.remove(path.size() - 1);
}
}关键点解析:
- 显式回溯 :
path是List类型,按引用传递。所有递归分支共享同一个path对象。因此,当一个节点的子树探索完毕,准备返回父节点时,必须通过path.remove(...)手动将当前节点从路径中移除,这便是"显式回溯" - 不可剪枝:因为题目要求找到"所有"路径,所以即使找到了第一条,也必须继续探索其他所有分支
拓展
注意,我们也可以这么做:合理设置 dfs 的参数 ,来优雅地避免手动回溯 路径列表吗,实现路径列表的自动回溯,且这种代码应该更好理解。参考代码如下(边搜索边记录结果):
java
class Solution {
List<String> result = new ArrayList<>();
// dfs 分左右子树搜索,并且每个递归栈帧校验(是否到达叶子节点,是则收集,否则回溯)
public List<String> binaryTreePaths(TreeNode root) {
if (root == null) {
return null;
}
// 从root开始dfs(path是不含)
dfs("", root);
return result;
}
/**
* @param path 当前收集到的路径(暂不含curNdoe)
* @param curNode 当前节点
*/
public void dfs(String path, TreeNode curNode) {
// 校验终止条件,就一个:到达叶子结点
if (curNode.left == null && curNode.right == null) {
result.add(path + curNode.val); // 拼接字符串
return;
}
// 搜索左子树
if (curNode.left != null) {
dfs(path + curNode.val + "->", curNode.left);
}
// 搜索右子树
if (curNode.right != null) {
dfs(path + curNode.val + "->", curNode.right);
}
}
}- 当然,上述代码含有大量字符串的连接和创建,这是一笔不小的开销,虽然可以提交通过,但是时间不低
- 后续的优化思路可以从这里下手,使用StringBuilder或者栈等数据结构优化,也可以达到 1ms 的提交,不过最终可能还是避免不了使用一些手动的回溯
最终兼顾效率与高可读性的参考代码(也是边搜索边记录结果):
javaclass Solution { List<String> result = new ArrayList<>(); public List<String> binaryTreePaths(TreeNode root) { if (root == null) { return result; } dfs(new StringBuilder(), root); return result; } public void dfs(StringBuilder pathBuilder, TreeNode node) { // 保存进入当前递归的路径情况(保存长度即可),用于后续回溯 int originalLength = pathBuilder.length(); // 先把当前节点值加上 pathBuilder.append(node.val); // 判断是否到达叶子节点 if (node.left == null && node.right == null) { result.add(pathBuilder.toString()); pathBuilder.setLength(originalLength); // 返回之前也要手动回溯一下! return; // 叶子节点直接返回 } // 非叶子节点,继续追加 "->" pathBuilder.append("->"); // 搜索左子树 if (node.left != null) { dfs(pathBuilder, node.left); } // 搜索右子树 if (node.right != null) { dfs(pathBuilder, node.right); } // 回溯当前层节点 pathBuilder.setLength(originalLength); } }
三、 核心对比与总结
| 特性 | LeetCode 112 (路径总和) | LeetCode 257 (二叉树的所有路径) |
|---|---|---|
| 问题目标 | 判断存在性 (返回 boolean) |
记录所有解 (返回 List<String>) |
| 遍历方式 | 深度优先搜索 (DFS) | 深度优先搜索 (DFS) |
| 回溯方式 | 隐式回溯 - 传递基本类型 int,按值传递,递归返回后自动恢复。 |
显式回溯 - 传递引用类型 List,必须手动 remove 恢复状态。 |
| 剪枝 | 可以剪枝 - 找到一个解后即可停止搜索。 | 不可剪枝 - 必须遍历整棵树找到所有解。 |
| 参数设计 | dfs(curSum, node) |
dfs(path, node) |
| 核心逻辑 | 在叶子节点判断 sum == target |
在叶子节点构建并保存 路径字符串 或者 边搜索边保存 |
总结:
通过对比这两道题,我们可以深刻理解回溯思想的两种实现方式:
- 当递归只需要传递数值(如
int,double)这类基本数据类型 时,通常是隐式回溯 - 当需要维护一个集合(如
List,Set,StringBuilder)这类引用数据类型 来记录路径或状态时,就必须进行显式回溯,在递归返回前手动恢复状态