目录
十大排序算法分类
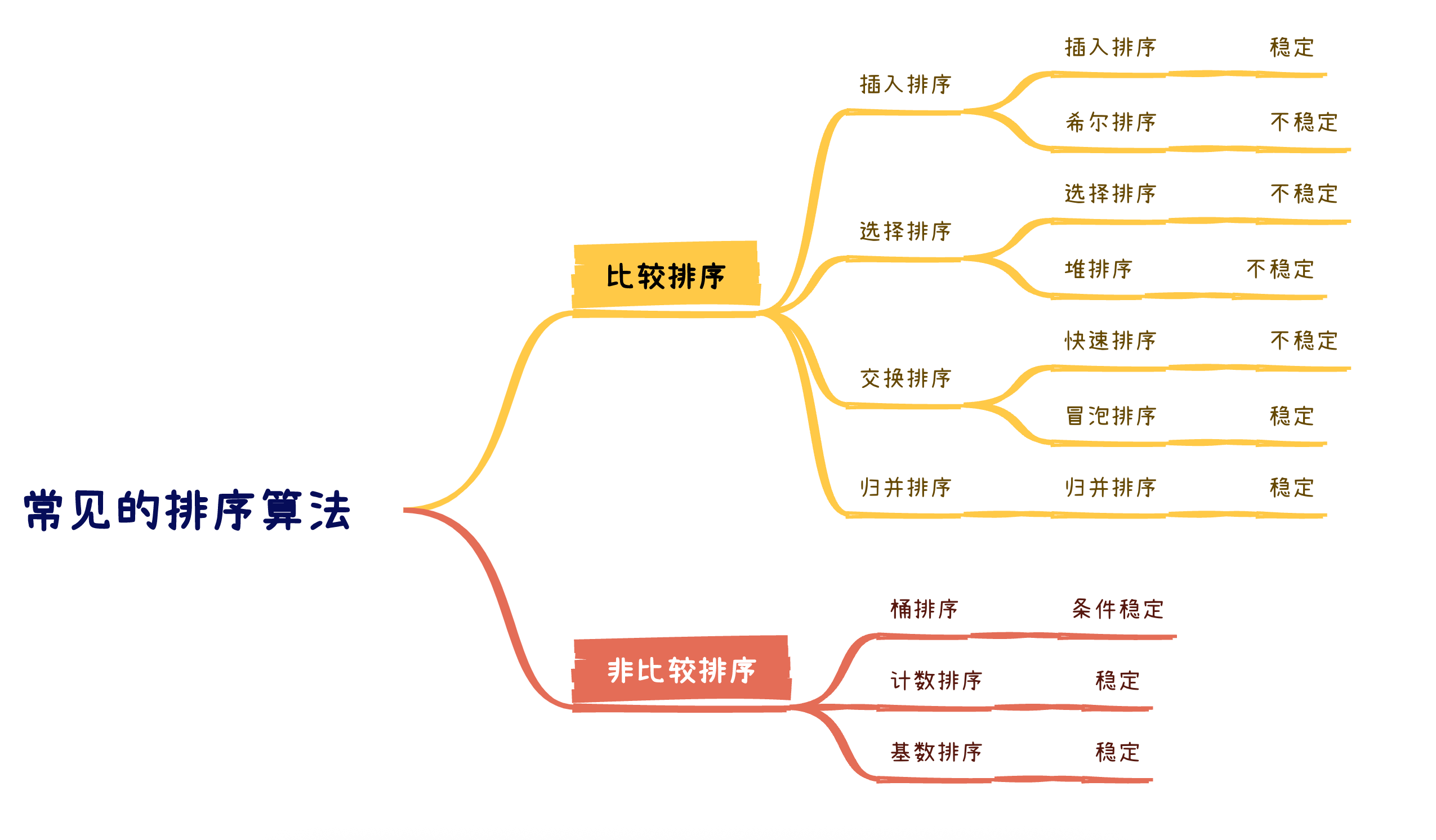 本篇分享十大排序算法中的 需要进行交换操作的选择排序 与堆排序, 其余算法也有介绍噢
本篇分享十大排序算法中的 需要进行交换操作的选择排序 与堆排序, 其余算法也有介绍噢
排序算法---插入排序(插入、希尔)(动图演示)-CSDN博客
排序算法---交换排序(冒泡、快速)(动图演示)-CSDN博客
选择排序
选择排序是一种简单直观的原地比较排序算法 ,无论数据是否有序,其时间复杂度均为 O(n²) ,因此适用于小规模数据 排序。它的主要优点是不占用额外内存空间 (空间复杂度 O(1)),但由于其低效的时间复杂度,不适合大规模数据排序。
算法步骤:
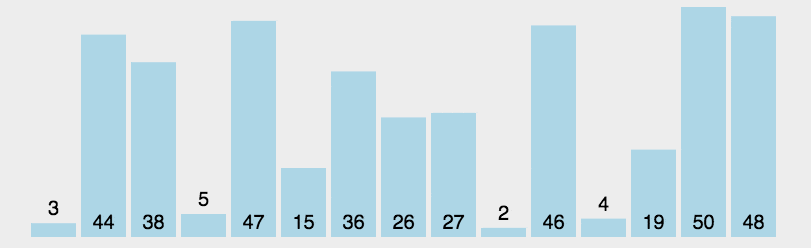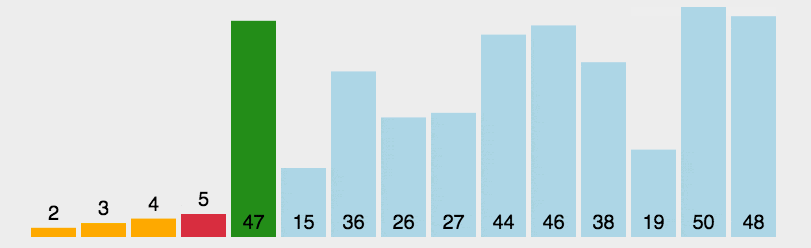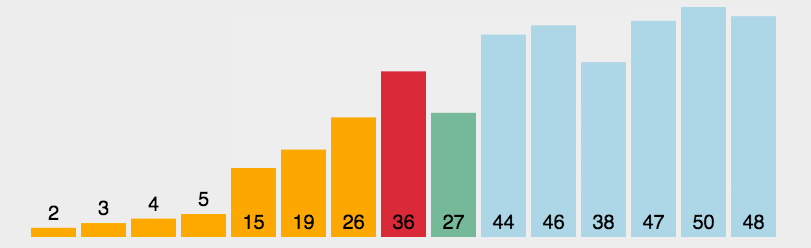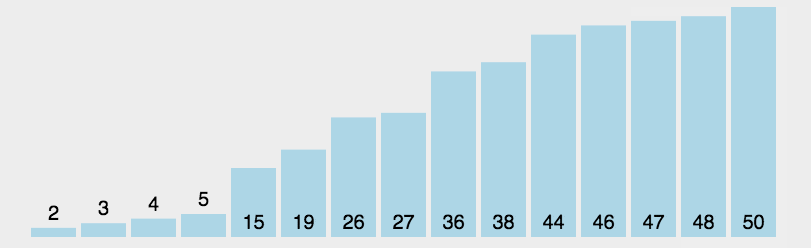
- 初始状态:最开始待排序序列为 arr[0......n-1] ,已排序序列为空
- 查找最小值:在待排序序列中找出最小值
- 交互位置:将最小值与待排序的第一个元素交互
- 重复执行:重复二三步,直到整个序列有序 (共需要n-1轮)
动图演示:
性能分析:
时间复杂度:
- 无论数据是否有序,均需两层循环比较O(n²)
空间复杂度:
- 仅需常数级额外空间 O(1)
稳定性:
- 不稳定 (交换时可能改变相同元素的相对元素)
代码实现(Java):
java
public class SelectionSort {
public static void selectionSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j; // 更新最小元素索引
}
}
// 交换 arr[i] 和 arr[minIndex]
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
public static void main(String[] args) {
int[] arr = {29, 10, 14, 37, 13};
selectionSort(arr);
System.out.println(Arrays.toString(arr)); // 输出 [10, 13, 14, 29, 37]
}
}堆排序
堆排序是一种基于二叉堆(Binary Heap) 数据结构的比较排序算法 ,属于选择排序 的优化版本。它通过构建最大堆(或最小堆)实现升序(或降序)排序,具有 O(n log n) 的时间复杂度,且是原地排序 (空间复杂度 O(1))。
算法步骤:
构建大根堆:
- 首先将待排序的数组构造成一个大根堆,此时整个数组的堆顶端元素就是最大元素交换
堆顶与末尾元素:
- 堆顶元素和数组末尾元素交换,此时末尾元素已有序(最大值)
排除末尾元素:
- 对剩余未排序部分n-1重新调整为最大堆,重复步骤2直到所有元素有序。
注意:升序用大根堆,降序就用小根堆(默认为升序)
动图演示:
首先我们给定一个无序的序列,将其看做一个堆结构,一个没有规则的二叉树,将序列里的值按照从上往下,从左到右依次填充到二叉树中。
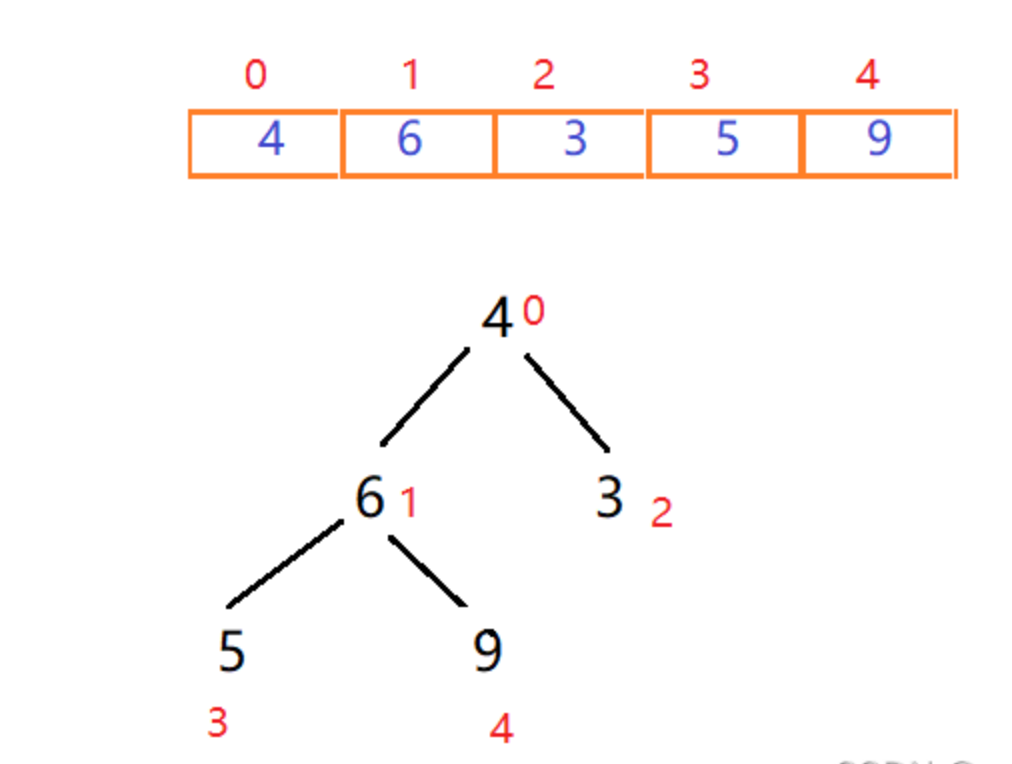
对于一个完全二叉树,在填满的情况下(非叶子节点都有两个子节点),每一层的元素个数是上一层的二倍,根节点数量是1,所以最后一层的节点数量,一定是之前所有层节点总数+1,所以,我们能找到最后一层的第一个节点的索引,即节点总数/2(根节点索引为0),这也就是第一个叶子节点,所以第一个非叶子节点的索引就是最后一个叶子结点的索引-1。那么对于填不满的二叉树呢?这个计算方式仍然适用,当我们从上往下,从左往右填充二叉树的过程中,第一个叶子节点,一定是序列长度/2,所以第最后一个非叶子节点的索引就是arr.len/2-1,对于此图数组长度为5,最后一个非叶子节点为5/2-1=1,即为6这个节点
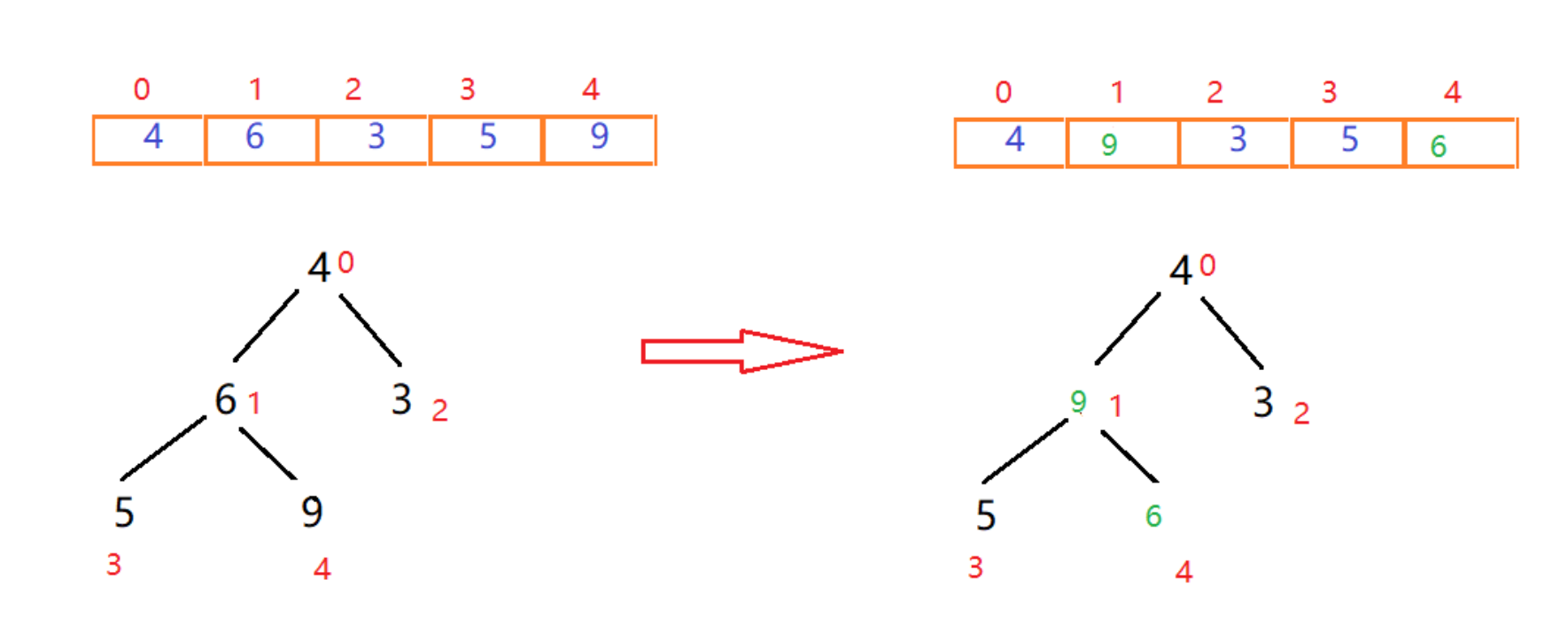
那么如何构建呢? 我们找到了最后一个非叶子节点,即元素值为6的节点,比较它的左右节点中最大的一个的值,是否比他大,如果大就交换位置。
在这里5小于6,而9大于6,则交换6和9的位置
找到下一个非叶子节点4,用它和它的左右子节点进行比较,4大于3,而4小于9,交换4和9位置
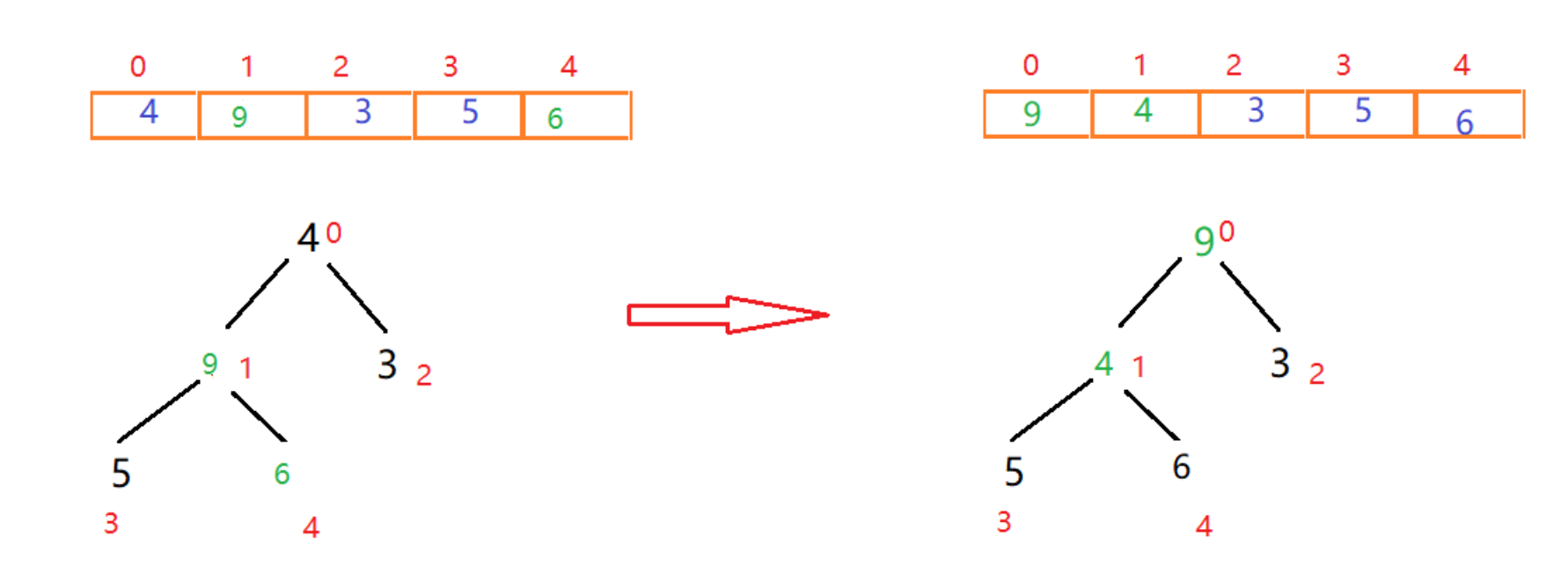
此时发现4小于5和6这两个子节点,我们需要进行调整,左右节点5和6中,6大于5且6大于父节点4,因此交换4和6的位置
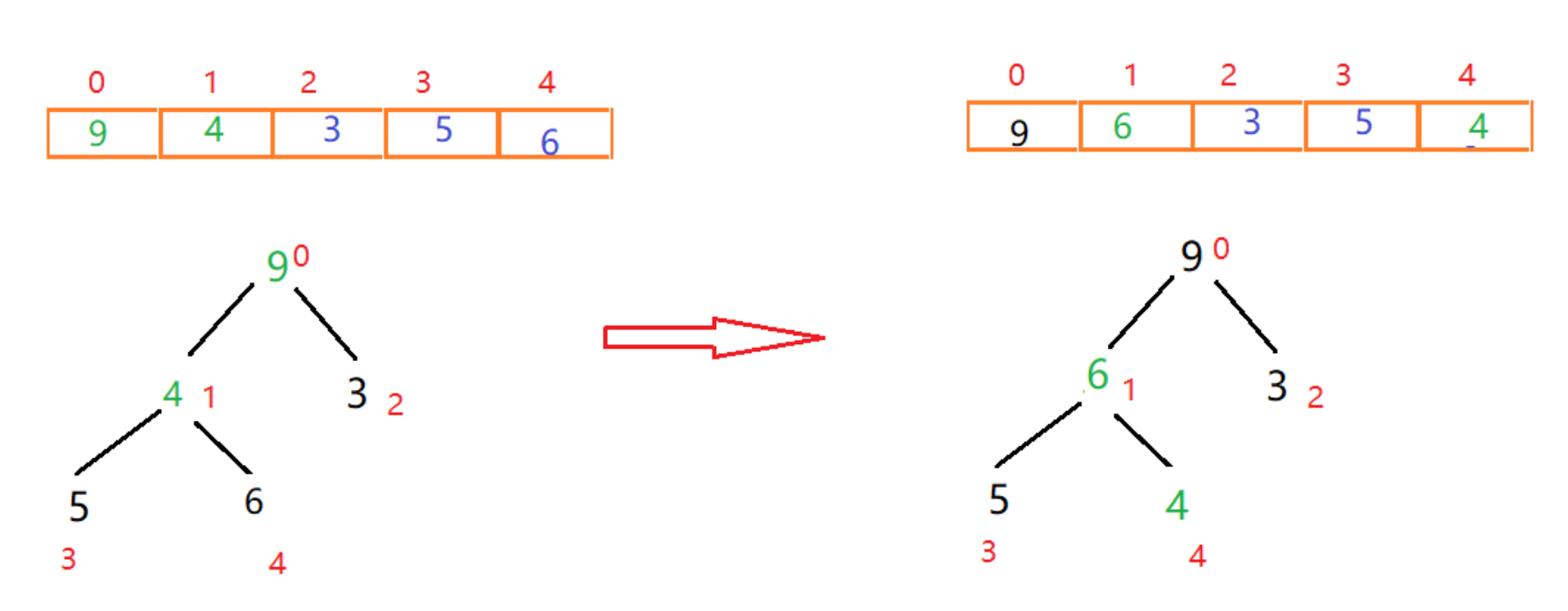
此时我们就构造出来一个大根堆,下来进行排序
首先将顶点元素9与末尾元素4交换位置,此时末尾数字为最大值。排除已经确定的最大元素,将剩下元素重新构建大根堆
一次交换重构如图:
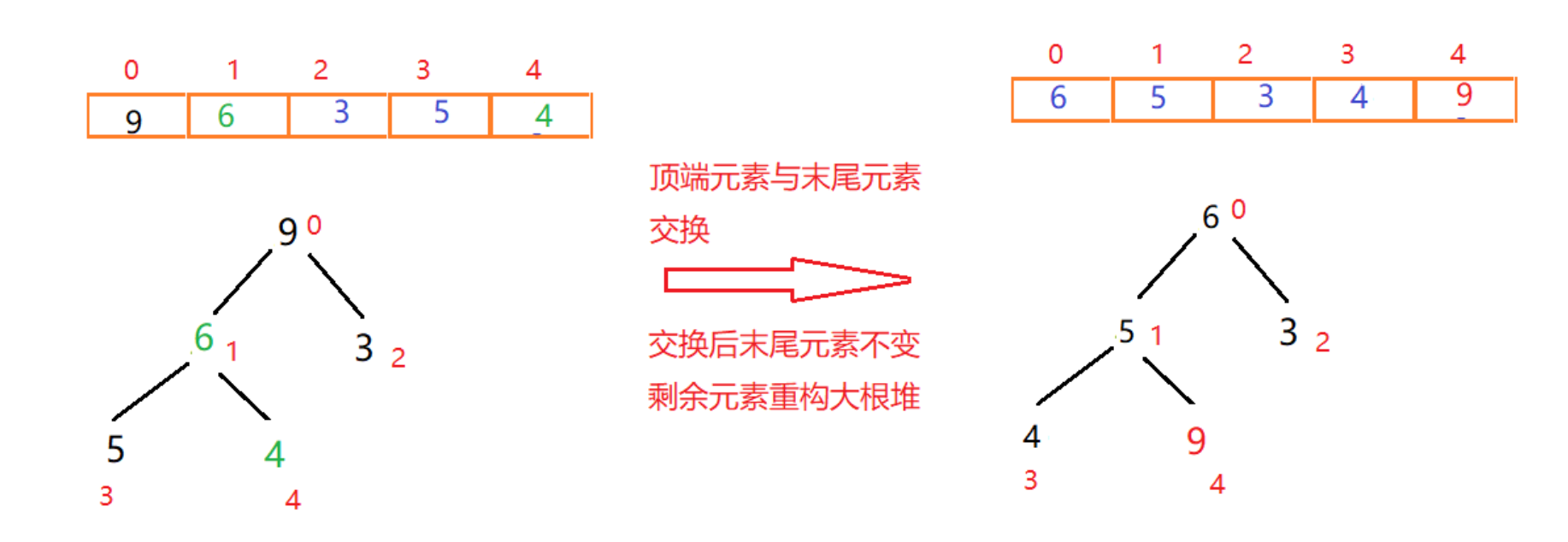
此时元素9已经有序,末尾元素则为4(每调整一次,调整后的尾部元素在下次调整重构时都不能动)
二次交换重构如图:
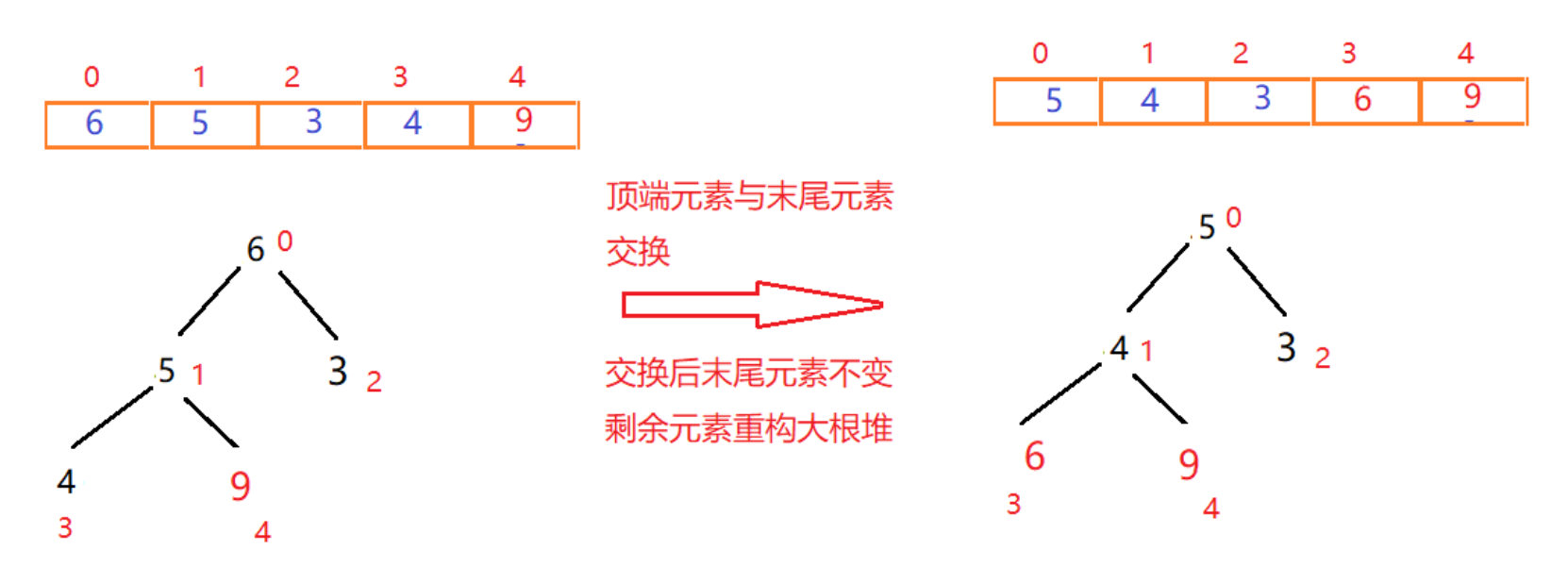
最终排序结果:

性能分析:
时间复杂度:
- 建堆O(n)+每次调整堆O(log n) 共O(n log n)
空间复杂度:
- 原地排序,无需额外空间 O(1)
稳定性:
- 不稳定
代码实现(Java):
java
public class HeapSort {
public static void heapSort(int[] arr) {
int n = arr.length;
// 1. 构建最大堆(从最后一个非叶子节点开始)
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// 2. 逐个提取堆顶元素并调整堆
for (int i = n - 1; i > 0; i--) {
// 交换堆顶和当前末尾元素
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// 调整剩余堆
heapify(arr, i, 0);
}
}
// 调整以节点i为根的子树为最大堆
private static void heapify(int[] arr, int n, int i) {
int largest = i; // 初始化根节点为最大值
int left = 2 * i + 1;
int right = 2 * i + 2;
// 比较左子节点
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// 比较右子节点
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// 若最大值不是根节点,则交换并递归调整
if (largest != i) {
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
heapify(arr, n, largest);
}
}
public static void main(String[] args) {
int[] arr = {4, 10, 3, 5, 1};
heapSort(arr);
System.out.println(Arrays.toString(arr)); // 输出 [1, 3, 4, 5, 10]
}
}