.
💓 博客主页:倔强的石头的CSDN主页
📝Gitee主页:倔强的石头的gitee主页
⏩ 文章专栏:《C++指南》
期待您的关注
文章目录
-
- 引言
- [一、C++ STL stack全景解析](#一、C++ STL stack全景解析)
-
- [1.1 容器适配器的本质](#1.1 容器适配器的本质)
- [1.2 核心价值剖析](#1.2 核心价值剖析)
- 二、stack核心操作深度解读
-
- [2.1 基础操作矩阵](#2.1 基础操作矩阵)
- [2.2 实战代码演练](#2.2 实战代码演练)
- 三、进阶应用场景
-
- [3.1 表达式求值](#3.1 表达式求值)
- [3.2 函数调用栈](#3.2 函数调用栈)
- [3.3 算法优化](#3.3 算法优化)
- 结语
引言
作为线性数据结构的经典代表,栈(stack)以其独特的后进先出(LIFO)特性,在函数调用、表达式求值、括号匹配等场景中扮演着关键角色。
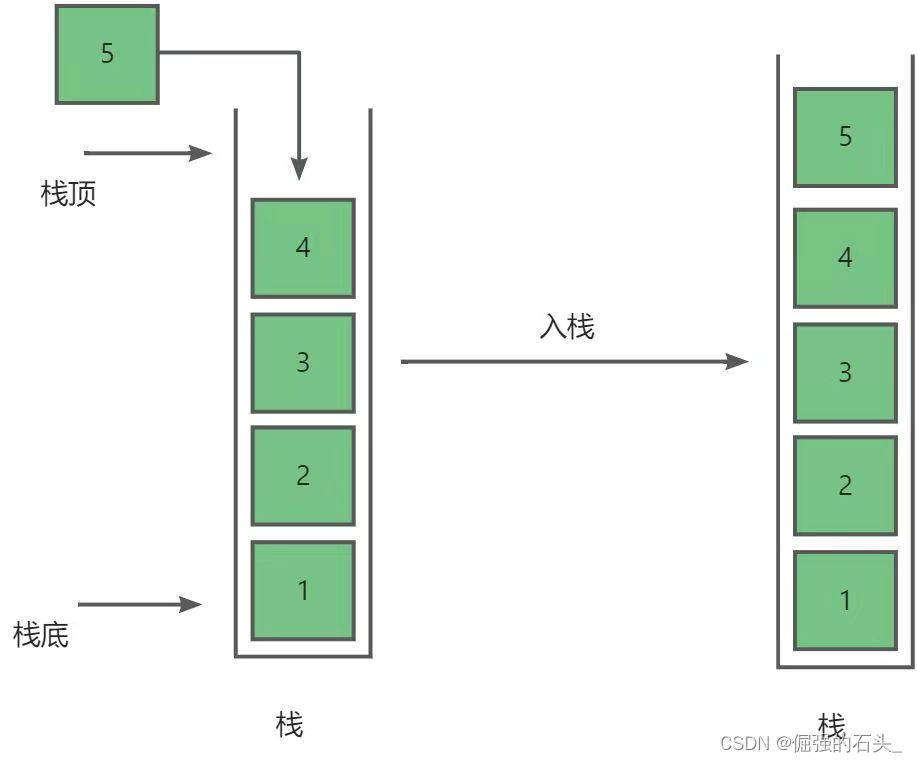
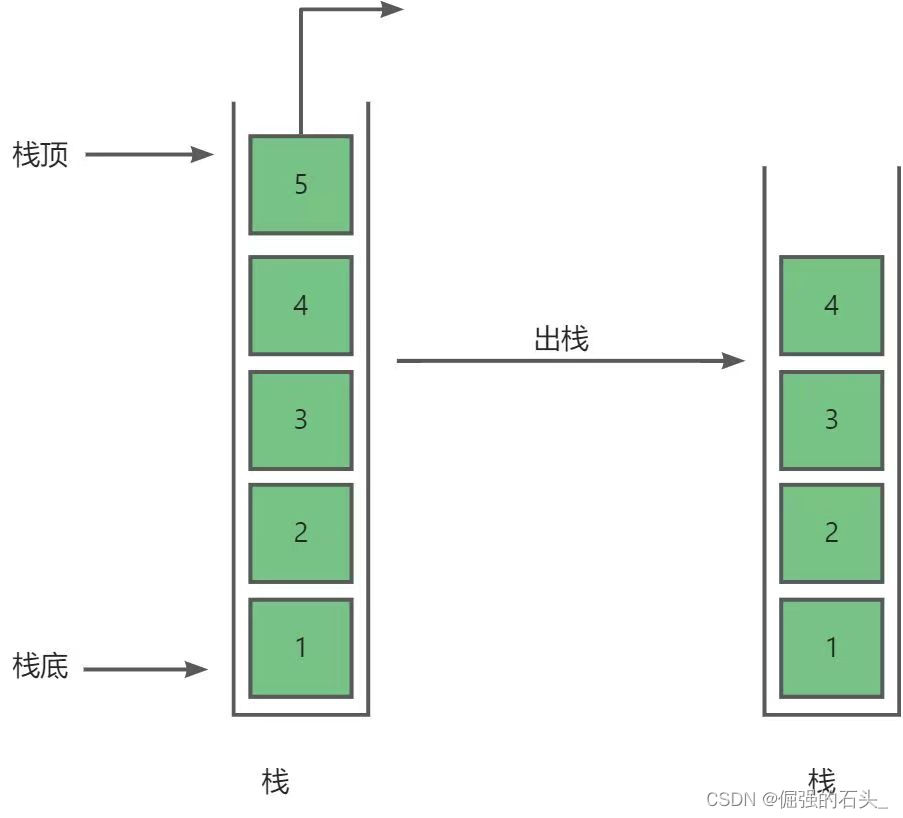
本文将深入解析C++ STL中的stack容器适配器,通过理论讲解与实战代码演示,帮助读者掌握这一重要工具的使用精髓。
本篇不仅适合初窥门径的新手,也能为经验丰富的开发者提供新的视角。
关于栈的结构的详细介绍,可以参考我之前写的一篇用C语言手搓栈的讲解文章
一、C++ STL stack全景解析
1.1 容器适配器的本质
stack并非独立的容器,而是构建于其他序列容器之上的容器适配器 。默认情况下,它使用deque作为底层容器,这种设计使其具有以下显著特点:
cpp
template <class T, class Container = deque<T> >
class stack;- 访问约束性:仅允许通过栈顶(top)进行元素操作
- 操作高效性:所有操作的时间复杂度均为O(1)
- 容器可置换性 :支持替换底层容器为
vector或list
1.2 核心价值剖析
- 接口简洁性:通过有限的接口规范操作,避免误用
- 类型安全性:模板机制保证元素类型统一
- 内存安全性:自动管理内存生命周期
- 算法适配性:天然适合需要LIFO特性的算法场景
二、stack核心操作深度解读
2.1 基础操作矩阵
| 操作 | 语法 | 时间复杂度 | 说明 |
|---|---|---|---|
| 压栈 | push(const T& val) | O(1) | 添加元素到栈顶 |
| 弹栈 | pop() | O(1) | 移除栈顶元素 |
| 访问栈顶 | top() | O(1) | 返回栈顶元素的引用 |
| 判空检测 | empty() | O(1) | 判断栈是否为空 |
| 容量查询 | size() | O(1) | 返回当前元素数量 |
2.2 实战代码演练
示例1:基础操作全流程
cpp
#include <iostream>
#include <stack>
int main() {
std::stack<int> s;
// 压栈操作
s.push(10); // 栈底 -> [10]
s.push(20); // [10, 20]
s.push(30); // 栈顶 -> [10, 20, 30]
// 访问栈顶
std::cout << "Top element: " << s.top() << std::endl; // 输出30
// 弹栈操作
s.pop(); // 移除30
s.pop(); // 移除20
// 判空检测
if (!s.empty()) {
std::cout << "Stack size: " << s.size() << std::endl; // 输出1
}
return 0;
}示例2:经典括号匹配算法
cpp
bool isBalanced(const std::string& expr) {
std::stack<char> s;
std::unordered_map<char, char> mapping = {
{')', '('},
{']', '['},
{'}', '{'}
};
for (char ch : expr) {
if (mapping.count(ch)) {
if (s.empty() || s.top() != mapping[ch])
return false;
s.pop();
} else {
s.push(ch);
}
}
return s.empty();
}
// 测试用例
std::cout << std::boolalpha;
std::cout << isBalanced("({[]})") << std::endl; // 输出true
std::cout << isBalanced("([)]") << std::endl; // 输出false三、进阶应用场景
3.1 表达式求值
栈在处理中缀表达式转后缀表达式(逆波兰表示法)时表现卓越:
cpp
std::string infixToPostfix(const std::string& infix) {
std::stack<char> op_stack;
std::string postfix;
// ... 转换逻辑(运算符优先级处理)
return postfix;
}关于逆波兰表达式的实践,单独写了一篇文章来讲解
【C++经典例题】逆波兰表达式求值:栈的经典应用与实现详解
3.2 函数调用栈
编译器使用调用栈管理函数调用关系:
cpp
void funcA() {
funcB(); // 压入调用栈
}
void funcB() {
// 返回时自动弹栈
}3.3 算法优化
在深度优先搜索(DFS)中,栈可替代递归实现:
cpp
void dfs(Node* root) {
std::stack<Node*> s;
s.push(root);
while (!s.empty()) {
Node* current = s.top();
s.pop();
// 处理节点
for (auto child : current->children) {
s.push(child);
}
}
}结语
通过对STL stack的系统性学习,我们不仅掌握了其基本操作,更领略了其在算法设计中的精妙应用。然而,这仅仅是冰山一角------stack的真正魅力在于其精巧的底层实现。
在下一篇文章中,我们将揭开stack的神秘面纱,深入探讨其底层容器选择策略,并手把手指导实现自定义栈结构。届时,您将真正理解STL设计者的智慧结晶,并能够根据特定需求优化栈的实现。
下篇预告:《解剖STL stack:从底层实现到自定义栈设计》------深入STL源码,解析deque的适配机制,并实现支持动态扩容的安全栈结构。
