目录
一、前言
在本章中,我们主要对图论进行介绍
- 图的基本概念,图的分类包括有向、无向图、连通图等。
- 图的存储结构,如邻接矩阵 和邻接表。
- 图的遍历,广度优先遍历和深度优先遍历。
- 图的最小生成树,Kruskal算法 和Prim算法。
- 图的最小生成路径,Dijkstra算法、Bellman-Ford算法和Floyd-Warshall算法。
二、图的基本概念
在现实生活中,如果我们想能够有效地表示和处理对象之间的复杂关系,我们之前学习到的数据结构就不够用了,比如我们生活中的地图导航系统,由此就引入了图这个数据结构,在图结构中,我们可以
- 清晰地表示城市之间的连接关系。
- 表达路径之间的权重(距离、时间等)。
- 使用图算法快速找到最优路径。
- 动态更新:如果某条路封路或拥堵,可以重新计算路径。
1、基本定义
图是由顶点集合及顶点间的关系组成的一种数据结构:G = (V , E),其中:
- 顶点集合 V = {x|x∈G中顶点} ,**V(G)**表示图G中顶点的有限非空集;
- 边集合 E = {(x,y)|x,y∈V} 或者 E = {<x, y>|x,y∈V && Path(x, y)} ,E(G) 是顶点间关系的有穷集合,也叫做边的集合。(x, y) 表示x到y的一条双向通路,即**(x, y)** 是无方向的;Path(x, y) 表示从x到y的一条单向通路,即**Path(x, y)**是有方向的。
2、相关概念
-
顶点和边 :图中结点称为顶点,第**
i** 个顶点记作**vi** 。两个顶点**vi** 和**vj** 相关联称作顶点**vi** 和顶点**vj** 之间有一条边,图中的第k条边记作**ek** ,ek = (vi,vj)或<vi,vj>。 -
有向图 :其中每条边都有一个方向 。顶点对
<x, y>是有序的,顶点对<<x, y>称为顶点x到顶点y的一条边(弧),<x, y>和**<y, x>**是两条不同的边。 -
无向图 :顶点对**
<x, y>** 是无序的,顶点对**<x, y>** 称为顶点x和顶点y相关联的一条边,这条边没有特定方向,<x, y>和**<y, x>**是同一条边。 -
有向完全图: 在n个顶点的有向图中,若有**
n * (n-1)**条边,即任意两个顶点之间有且仅有方向相反的边。 -
无向完全图: 在有n个顶点的无向图中,若有**
n * (n-1)/2**条边,即任意两个顶点之间有且仅有一条边。 -
邻接顶点: 在无向图中G中,若**
<x, y>** 是E(G)中的一条边,则称 x 和 y 互为邻接顶点,并称边**<x, y>** 依附于顶点 x 和 y;在有向图G中,若**<x, y>** 是E(G)中的一条边,则称顶点 x 邻接到y,顶点 y 邻接自顶点 x,并称边**<x, y>**与顶点 x 和顶点 y 相关联。 -
顶点的度: 顶点 v 的度是指与它相关联的边的条数,记作
deg(v)。对于有向图,顶点的度等于该顶点的入度与出度之和,其中顶点v的入度是以v为终点的有向边的条数,记作indev(v);顶点v的出度是以v为起始点的有向边的条数,记作outdev(v)。因此:dev(v) = indev(v) + outdev(v)。对于无向图,顶点的度等于该顶点的入度和出度,即dev(v) = indev(v) = outdev(v)。 -
路径 :在图 G = (V , E) 中,若从顶点 vi 出发有一组边使其可到达顶点
vj,则称顶点 vi 到顶点 vj 的顶点序列为从顶点 vi 到顶点 vj 的路径。 -
路径长度: 对于不带权的图,一条路径的路径长度是指该路径上的边的条数 ;对于带权的图,一条路径的路径长度是指该路径上各个边权值的总和。
-
子图: 设图G = (V , E) 和图 G = (V1 , E1) ,若 V1 属于 V 且 E1 属于 E ,则称 G1 是 G的子图。
-
**连通图:**在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。
-
强连通图:在有向图中,若在每一对顶点vi和vj之间都存在一条从vi到vj的路径,也存在一条从vj到vi的路径,则称此图是强连通图。
-
**生成树:**一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。
三、图的存储结构
图的存储结构决定了图的表示方式、操作效率以及内存使用情况。常见的图存储结构主要有两种:邻接矩阵(Adjacency Matrix) 和 邻接表(Adjacency List)。
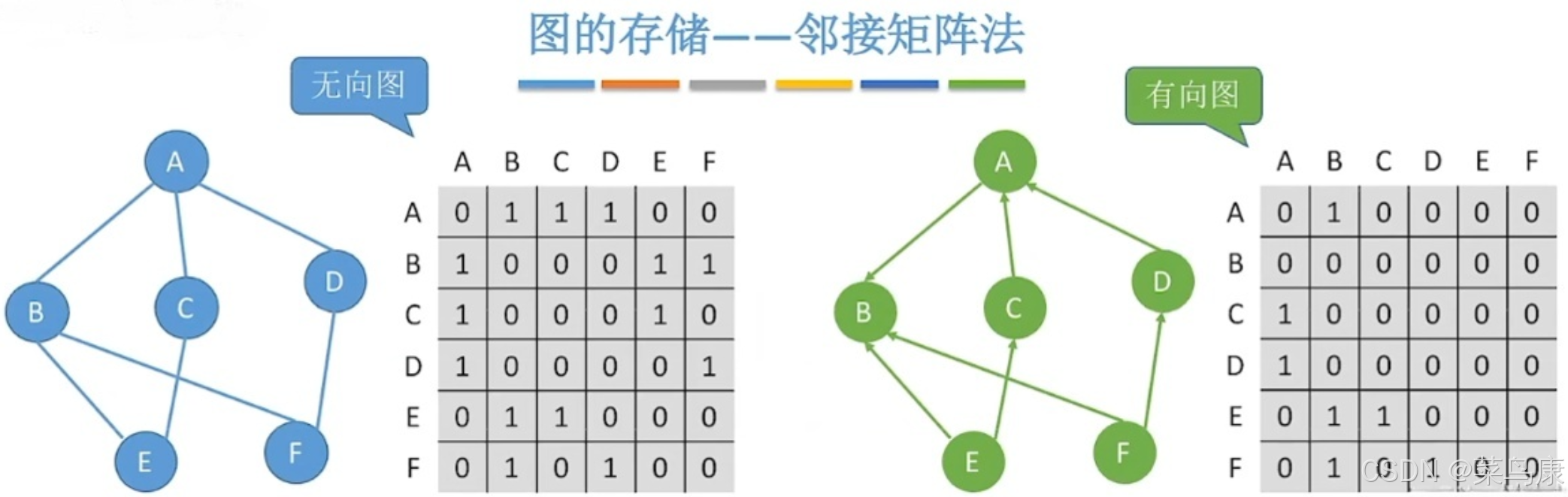
1、邻接矩阵
邻接矩阵是一种使用二维数组来表示图的方法。对于一个有 n个顶点的图,它的邻接矩阵是一个 n×n 的矩阵,其中元素 A[i][j] 表示顶点 i到顶点 j是否有一条边相连(对于无权图)或者这条边的权重(对于带权图)。
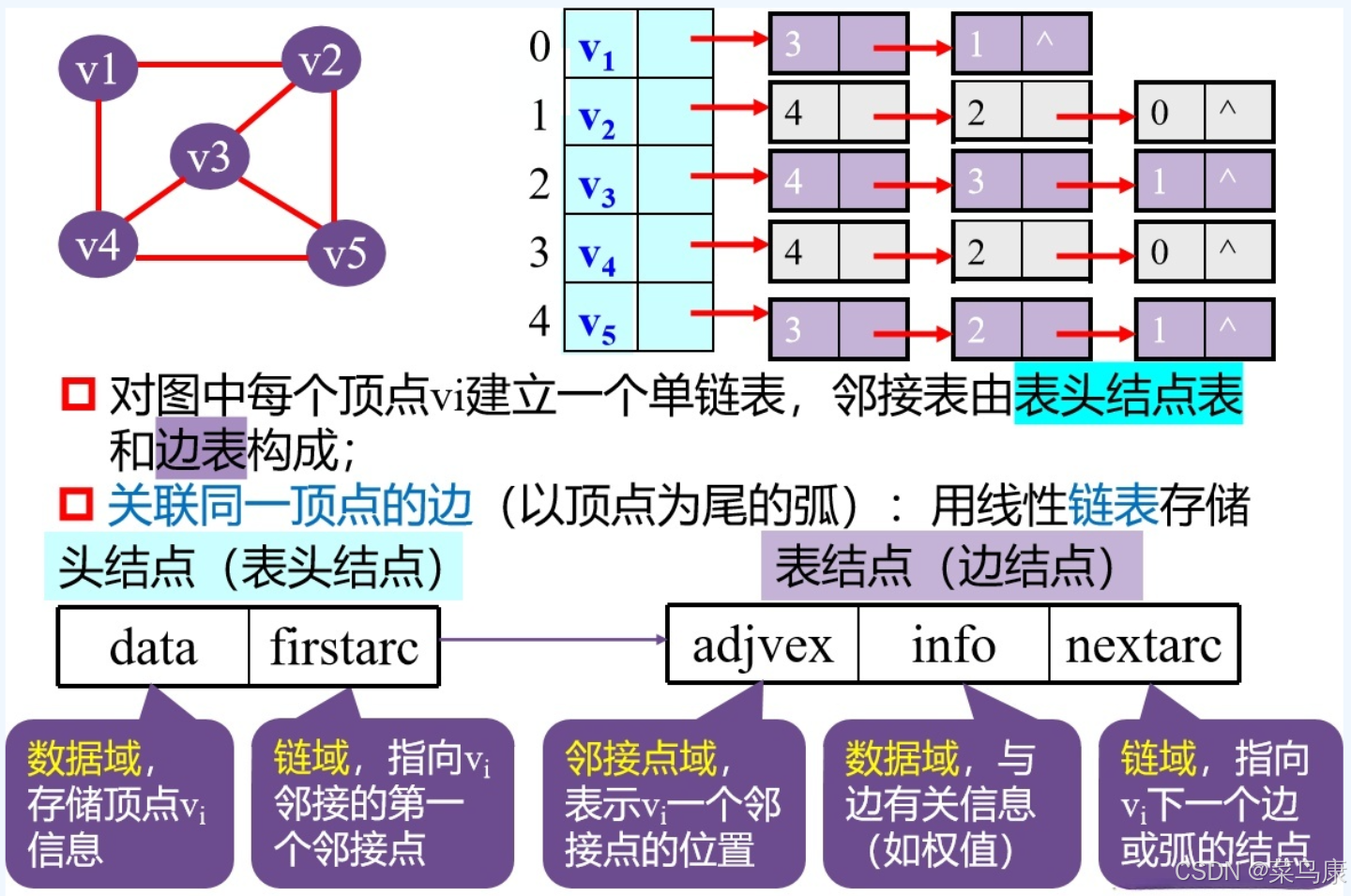
2、邻接表
邻接表是一种利用链表或数组等数据结构来表示每个顶点与其相邻顶点的关系的方法。对于每个顶点,维护一个列表(通常是一个动态数组、链表或哈希集合),包含所有与该顶点直接相连的其他顶点的信息(可能是终点和权重)。
四、代码实现
1、基于邻接矩阵的图的C++实现
使用函数模板来实现图
cpp
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
public:
struct Edge
{
V _srci;//源点
V _dsti;//终点
W _w;//边的权重
Edge(const V& srci, const V& dsti, const W& w)
:_srci(srci)
,_dsti(dsti)
,_w(w)
{}
bool operator<(const Edge& eg) const
{
return _w < eg._w;
}
bool operator>(const Edge& eg) const
{
return _w > eg._w;
}
};
private:
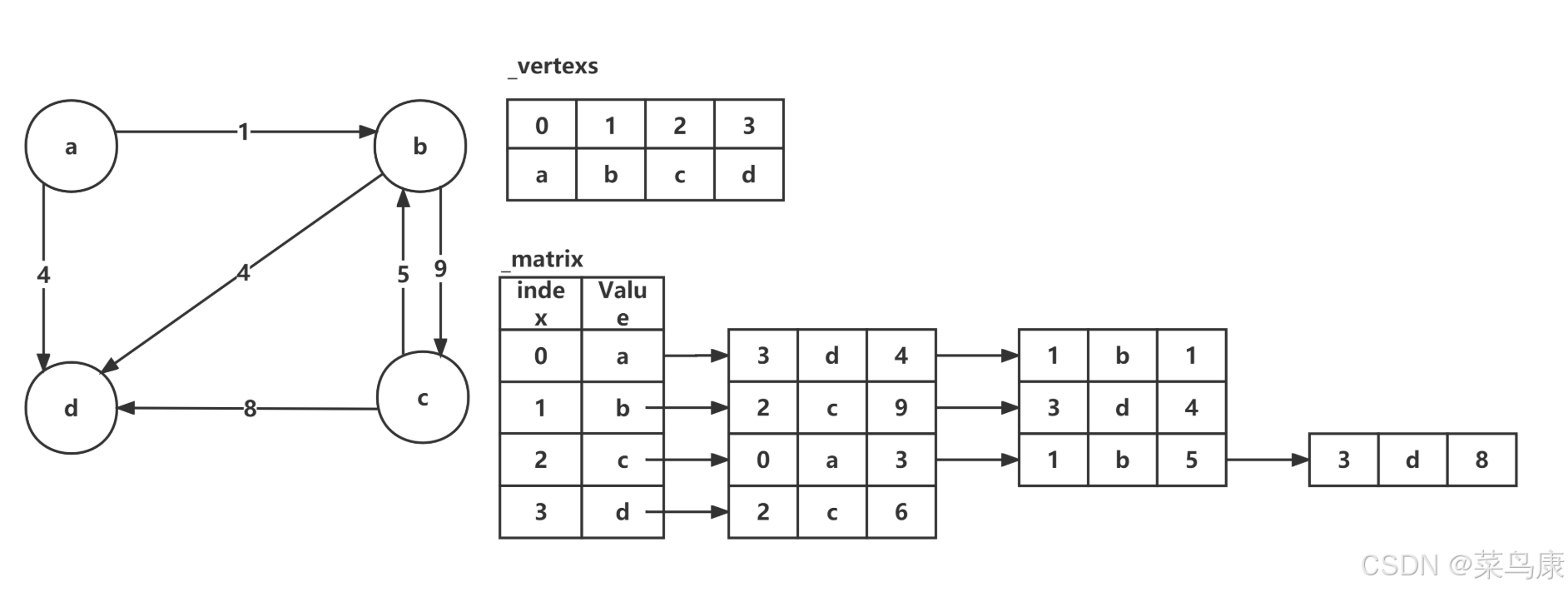
map<V, size_t> _vIndexMap;
vector<V> _vertexs; // 顶点集合
vector<vector<W>> _matrix; // 存储边集合的矩阵
};对于图:
- 需要将顶点和边表示出来,顶点我们就用数组 _vertexs来存储。
- 还需要一个数据结构 map 将图中的顶点值映射到其在邻接矩阵中的索引。如果顶点是 "A"、"B"、"C",那么 _vIndexMap["A"] = 0; _vIndexMap["B"] = 1; _vIndexMap["C"] = 2;
- 再来一个存储边集合的矩阵 _matrix
对于图中的边:
- 我们定义一个结构体 Edge 表示边,里面需要一条边的两个顶点和该边的权重。还需要重载**> 、<**用于比较边的权重大小(后面的Kruskal 和 Dijkstra 算法会用到)。
图的默认构造函数和带参构造函数
cpp
typedef Graph<V, W, MAX_W, Direction> Self;//为当前模板类创建一个简短的别名,方便在类内部引用自身
Graph() = default;//默认构造函数
Graph(const V* vertexs, size_t n)//使用顶点数组初始化图
{
_vertexs.reserve(n);
for (size_t i = 0; i < n; ++i)
{
_vertexs.push_back(vertexs[i]);
_vIndexMap[vertexs[i]] = i;
}
// MAX_W 作为不存在边的标识值
_matrix.resize(n);//,二维邻接矩阵,调整外层vector大小为n(顶点数量)
for (auto& e : _matrix)//遍历每一行
{
e.resize(n, MAX_W);//调整每行的大小为n,并用MAX_W填充
}
}
获取顶点索引方法,给定要查询的顶点返回该顶点的索引。
cpp
size_t GetVertexIndex(const V& v)
{
auto ret = _vIndexMap.find(v);
if (ret != _vIndexMap.end())
{
return ret->second;
}
else
{
throw invalid_argument("不存在的顶点");
return -1;
}
}在图中添加边
cpp
void _AddEdge(size_t srci, size_t dsti, const W& w)//直接给定顶点的索引
{
_matrix[srci][dsti] = w;
if (Direction == false)//无向图的情况
{
_matrix[dsti][srci] = w;
}
}
void AddEdge(const V& src, const V& dst, const W& w)//给定顶点
{
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
_AddEdge(srci, dsti, w);
}打印图
cpp
void Print()
{
// 打印顶点和下标映射关系
for (size_t i = 0; i < _vertexs.size(); ++i)
{
cout << _vertexs[i] << "-" << i << " ";
}
cout << endl << endl;
cout << " ";
for (size_t i = 0; i < _vertexs.size(); ++i)
{
cout << i << " ";
}
cout << endl;
// 打印矩阵
for (size_t i = 0; i < _matrix.size(); ++i)
{
cout << i << " ";
for (size_t j = 0; j < _matrix[i].size(); ++j)
{
if (_matrix[i][j] != MAX_W)
cout << _matrix[i][j] << " ";
else
cout << "#" << " ";
}
cout << endl;
}
cout << endl << endl;
// 打印所有的边
for (size_t i = 0; i < _matrix.size(); ++i)
{
for (size_t j = 0; j < _matrix[i].size(); ++j)
{
if (i < j && _matrix[i][j] != MAX_W)
{
cout << _vertexs[i] << "-" << _vertexs[j] << ":" << _matrix[i][j] << endl;
}
}
}
}测试:
图的创建
1、IO输入 -- 不方便测试,oj中更适合
2、图结构关系写到文件,读取文件
3、手动添加边
以添加边的方式生成如下图
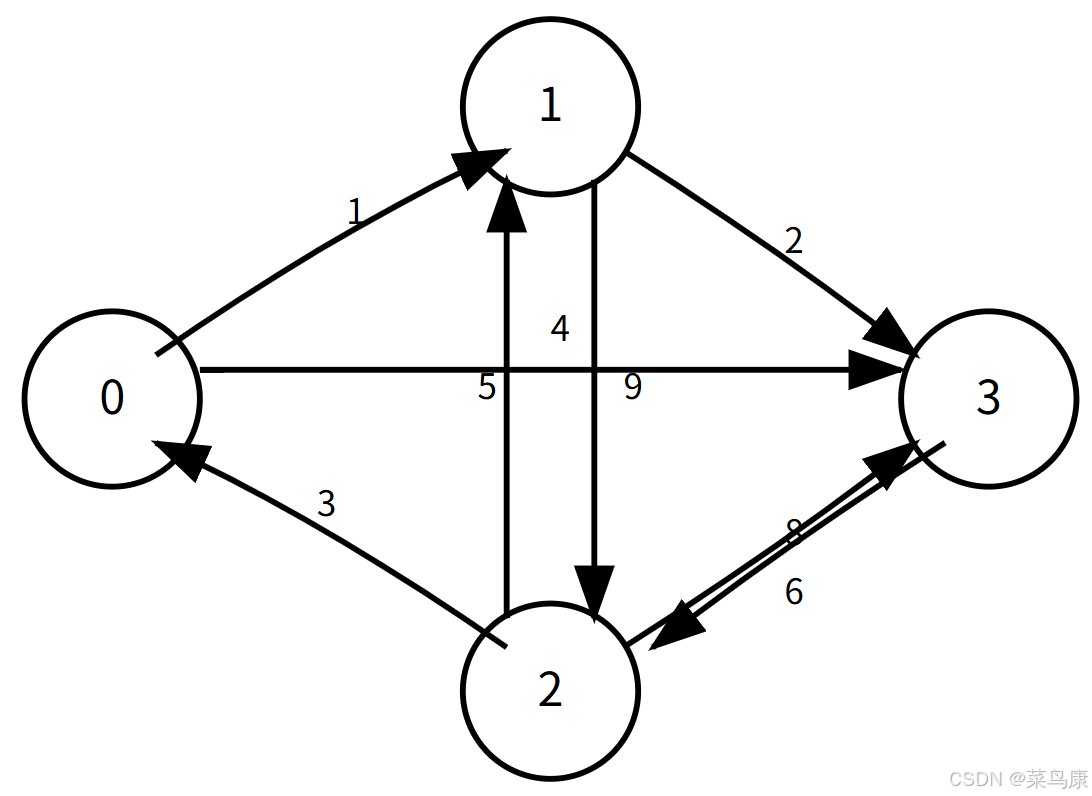
cpp
void TestGraph()
{
Graph<char, int, INT_MAX, true> g("0123", 4);
g.AddEdge('0', '1', 1);
g.AddEdge('0', '3', 4);
g.AddEdge('1', '3', 2);
g.AddEdge('1', '2', 9);
g.AddEdge('2', '3', 8);
g.AddEdge('2', '1', 5);
g.AddEdge('2', '0', 3);
g.AddEdge('3', '2', 6);
g.Print();
}
cpp
#include "Graph.h"
int main()
{
Matrix::TestGraph();
return 0;
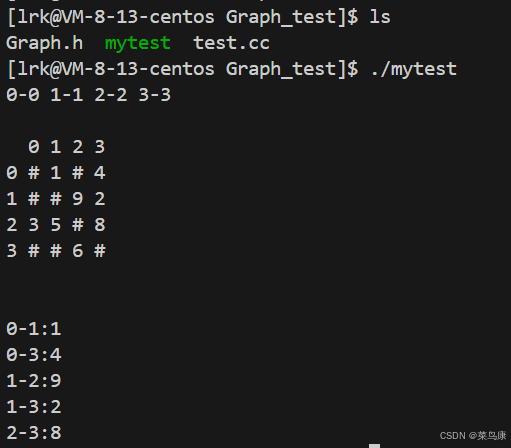
}结果如下图所示
2、基于邻接表的图的C++实现
同样使用函数模板来实现,实现上面的几个功能
cpp
namespace link_table
{
template<class W>
struct Edge
{
//int _srci;
int _dsti; // 目标点的下标
W _w; // 权值
Edge<W>* _next;
Edge(int dsti, const W& w)
:_dsti(dsti)
, _w(w)
, _next(nullptr)
{}
};
template<class V, class W, bool Direction = false>
class Graph
{
typedef link_table::Edge<W> Edge;
public:
Graph(const V* a, size_t n)
{
_vertexs.reserve(n);
for (size_t i = 0; i < n; ++i)
{
_vertexs.push_back(a[i]);
_indexMap[a[i]] = i;
}
_tables.resize(n, nullptr);
}
size_t GetVertexIndex(const V& v)
{
auto it = _indexMap.find(v);
if (it != _indexMap.end())
{
return it->second;
}
else
{
//assert(false);
throw invalid_argument("顶点不存在");
return -1;
}
}
void AddEdge(const V& src, const V& dst, const W& w)
{
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
// 1->2
Edge* eg = new Edge(dsti, w);
eg->_next = _tables[srci];
_tables[srci] = eg;//更新头顶点
// 2->1
if (Direction == false)
{
Edge* eg = new Edge(srci, w);
eg->_next = _tables[dsti];
_tables[dsti] = eg;
}
}
void Print()
{
// 顶点
for (size_t i = 0; i < _vertexs.size(); ++i)
{
cout << "[" << i << "]" << "->" << _vertexs[i] << endl;
}
cout << endl;
for (size_t i = 0; i < _tables.size(); ++i)
{
cout << _vertexs[i] << "[" << i << "]->";
Edge* cur = _tables[i];
while (cur)
{
cout <<"["<<_vertexs[cur->_dsti] << ":" << cur->_dsti << ":"<<cur->_w<<"]->";
cur = cur->_next;
}
cout <<"nullptr"<<endl;
}
}
private:
vector<V> _vertexs; // 顶点集合
map<V, int> _indexMap; // 顶点映射下标
vector<Edge*> _tables; // 邻接表
};
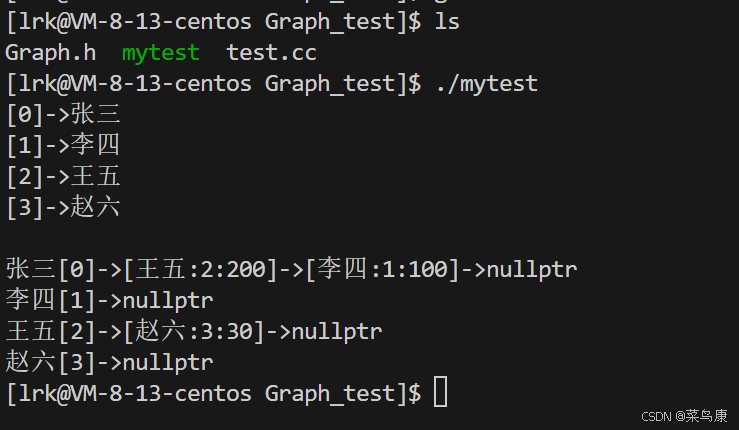
void TestGraph1()
{
string a[] = { "张三", "李四", "王五", "赵六" };
Graph<string, int, true> g1(a, 4);
g1.AddEdge("张三", "李四", 100);
g1.AddEdge("张三", "王五", 200);
g1.AddEdge("王五", "赵六", 30);
g1.Print();
}
}使用一个map将图中的顶点值映射到其在邻接表中的索引,顶点就用数组 _vertexs 来存储,边的信息使用一个结构体存储,由于在邻接表中,每个链表节点表示从当前顶点出发的一条边,起点(_srcI)是已知的 ,因此 _srcI是多余的,因此边的结构体中只包含终点,边的权值,该顶点指向的其他边。边的集合的邻接表我们利用vector来存储。
边的添加流程如下:
添加边A→B(权重5):
- 获取A的索引0,B的索引1
- 创建边对象0→1(5),插入A的邻接表
- 如果是无向图,再创建1→0(5),插入B的邻接表
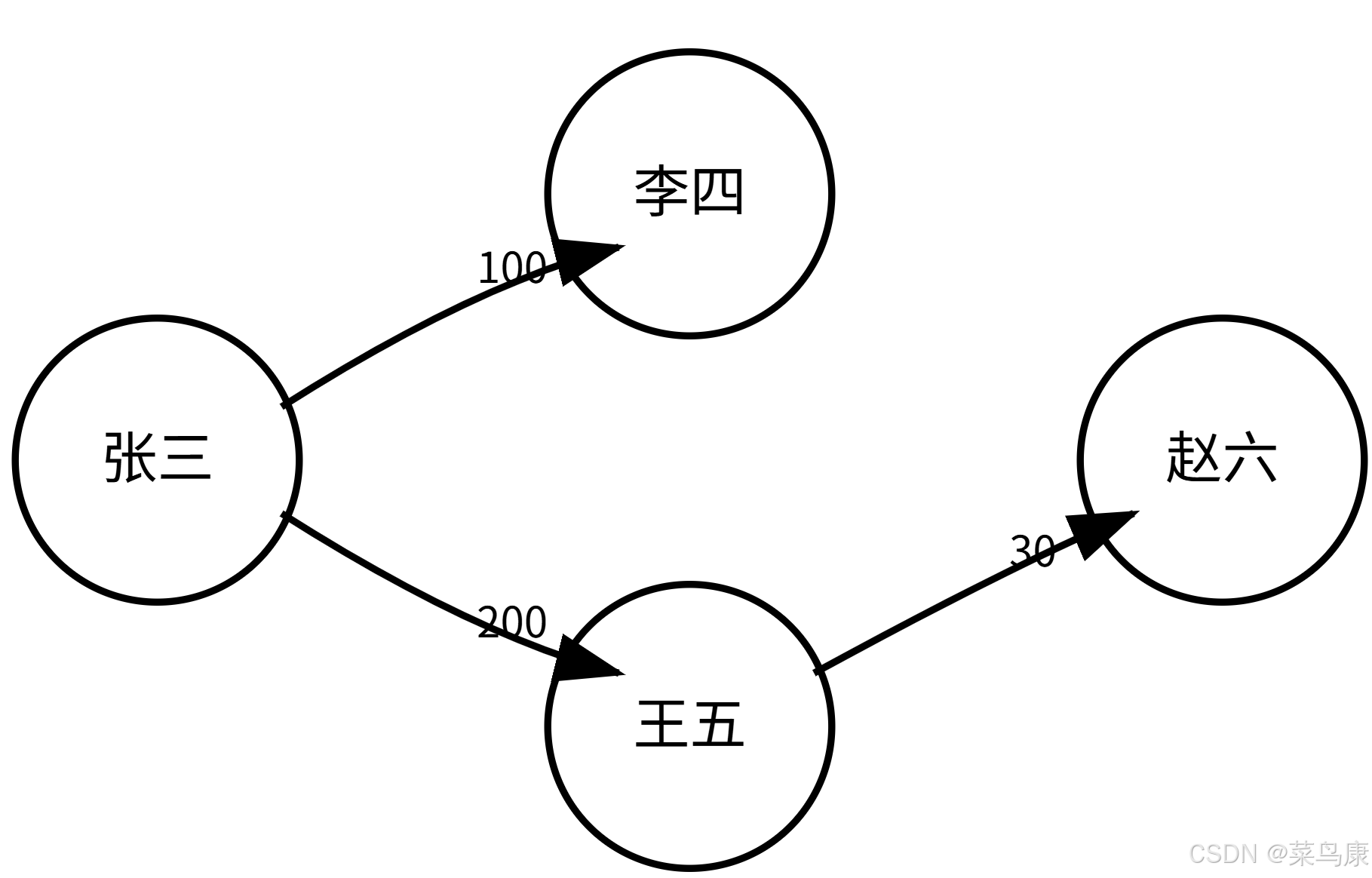
结果如图所示
五、图的遍历
给定一个图G和其中任意一个顶点v0,从v0出发,沿着图中各边访问图中的所有顶点,且每个顶 点仅被遍历一次。以下的图的遍历都是基于以邻接矩阵实现的图。
1、广度优先遍历
广度优先遍历(Breadth First Search),又称为广度优先搜索,简称BFS。
先举个例子来说:
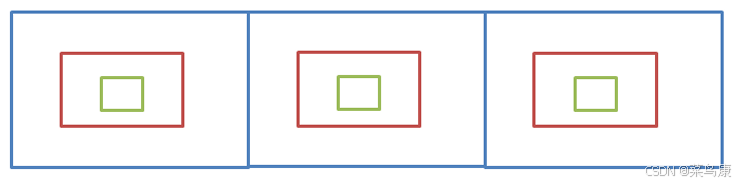
如下有三个抽屉,每个抽屉里面都套着两层抽屉。
比如现在要找东西,假设有三个抽屉,东西在那个抽屉不清楚,现在要将其找到,广度优先遍历的做法是:
- 先将三个抽屉打开,在最外层找一遍
- 将每个抽屉中红色的盒子打开,再找一遍
- 将红色盒子中绿色盒子打开,再找一遍
直到找完所有的盒子,注意:每个盒子只能找一次,不能重复找
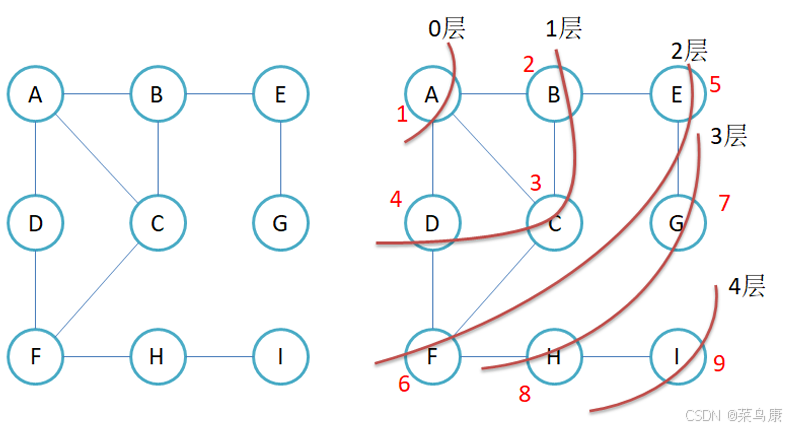
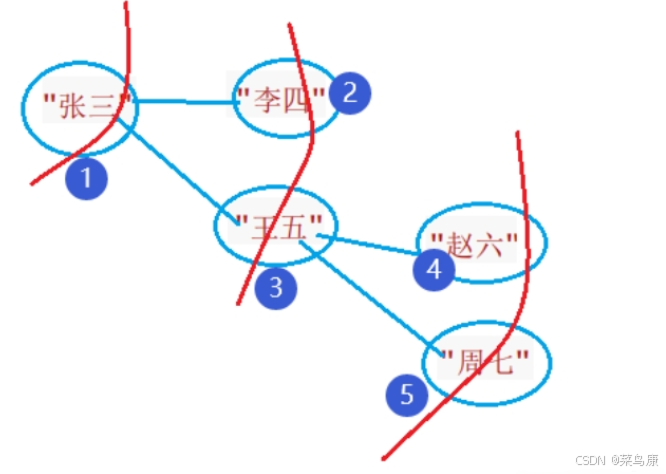
图的广度优先遍历图示
这就是对一个图(无向图)的广度优先遍历,红色的数字就是结点遍历的顺序。 其实就是一层一层的遍历,这里是从A这个顶点开始,所以先遍历结点A,然后依次遍历与A直接相连的一层的结点,接着逐层向外扩展,直到遍历完所有可达的节点。
广度优先遍历是一种分层的查找过程,每向前走一步可能访问一批顶点 ,不像深度优先搜索那样有往回退的情况,因此它不是一个递归的算法。为了实现逐层的访问,算法必须借助一个辅助队列,以记忆正在访问的顶点的下一层顶点。
广度优先遍历的实现:
图的广度优先遍历跟二叉树的层序遍历差不多,我们都是需要一个队列来辅助,就按上面的图示,我们来进行广度优先遍历。
首先从顶点A开始,先让A入队列

判断队列是否为空,队列不为空,出队头元素A,然后我们打印一下A的值,那这个顶点就遍历过去了,然后把与A直接相连的顶点BCD入队列

队列不为空,继续出队头元素B,然后把与B直接相连的顶点入队列,但是这里就出现了问题,我们接着要把B直接相连的顶点A、C、E入队列,但是我们知道A已经入过队列遍历过了,且C此时还存在于队列中,这该怎么办呢?
我们可以考虑对已经遍历过的顶点进行标记,后续只对未标记的进行入队,开一个数组,默认都给false,遍历一个结点,就把对应下标位置的值改为true,表示这个结点已经被遍历过了。
那么什么时候进行标记呢?打印之前标记还是打印之后标记呢?如果打印之后标记的话,B出队列之后其实还会把C带到队列里面,因为B出队列,然后打印B,此时A已经打印过了被标记了,但是C还没有出队列打印,所以C还没有被标记,所以B打印之后入与B直接相连的顶点ACE的时候,A不会入,但是C还会入。所以我们考虑一个顶点入队列的时候我们就去标记它,这样就不会出现上面的情况(队列里面出现重复顶点)
代码实现
cpp
void BFS(const V& src)
{
size_t srci = GetVertexIndex(src);//从该点出发进行广度优先遍历
// 队列和标记数组
queue<int> q;//队列
vector<bool> visited(_vertexs.size(), false);//标记数组,并初始化为false
q.push(srci);//将顶点先加入队列中
visited[srci] = true;//加入队列后标记为true
int levelSize = 1;//表示层数,当前在第几层
size_t n = _vertexs.size();
while (!q.empty())//如果队列非空
{
// 一层一层出
for (int i = 0; i < levelSize; ++i)
{
int front = q.front();
q.pop();
cout << front << ":" << _vertexs[front] << " ";
// 把front顶点的邻接顶点入队列
for (size_t i = 0; i < n; ++i)
{
if (_matrix[front][i] != MAX_W)
{
if (visited[i] == false)
{
q.push(i);
visited[i] = true;
}
}
}
}
cout << endl;
levelSize = q.size();
}
cout << endl;
} 测试
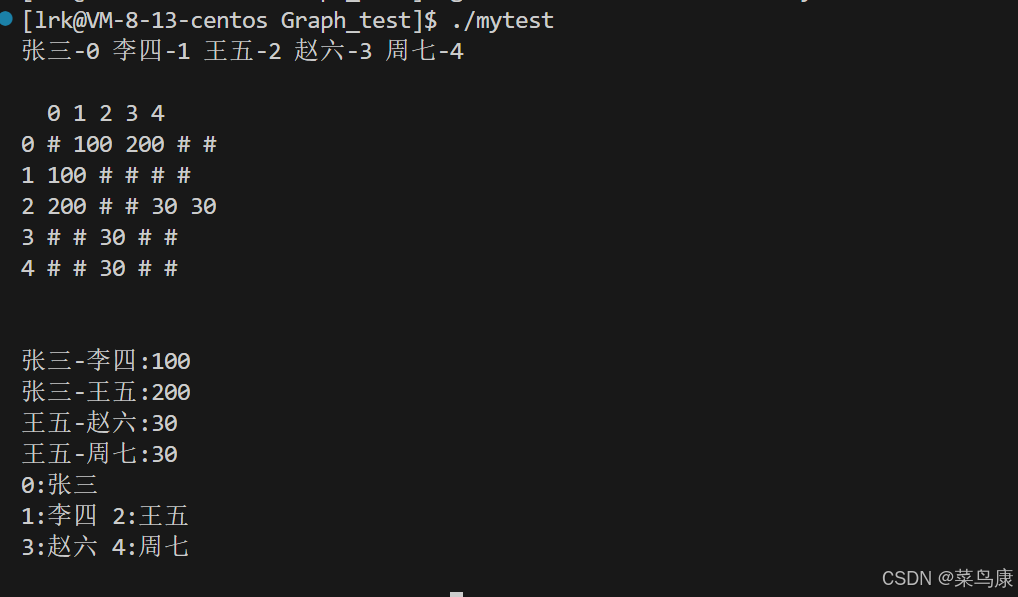
cpp
void TestBDFS()
{
string a[] = { "张三", "李四", "王五", "赵六", "周七" };
Graph<string, int> g1(a, sizeof(a) / sizeof(string));
g1.AddEdge("张三", "李四", 100);
g1.AddEdge("张三", "王五", 200);
g1.AddEdge("王五", "赵六", 30);
g1.AddEdge("王五", "周七", 30);
g1.Print();
g1.BFS("张三");
g1.DFS("张三");
}
2、深度优先遍历
深度优先遍历(Depth-First Search,简称 DFS)
比如现在要找东西,假设有三个抽屉,东西在那个抽屉不清楚,现在要将其找到,广度优先遍历的做法是:
- 先将第一个抽屉打开,在最外层找一遍
- 将第一个抽屉中红盒子打开,在红盒子中找一遍
- 将红盒子中绿盒子打开,在绿盒子中找一遍
- 递归查找剩余的两个盒子
深度优先遍历:将一个抽屉一次性遍历完(包括该抽屉中包含的小盒子),再去递归遍历其他盒子
如同我们在二叉树中学习到的前序遍历,先往前深走,直到走不通了再返回来回溯。
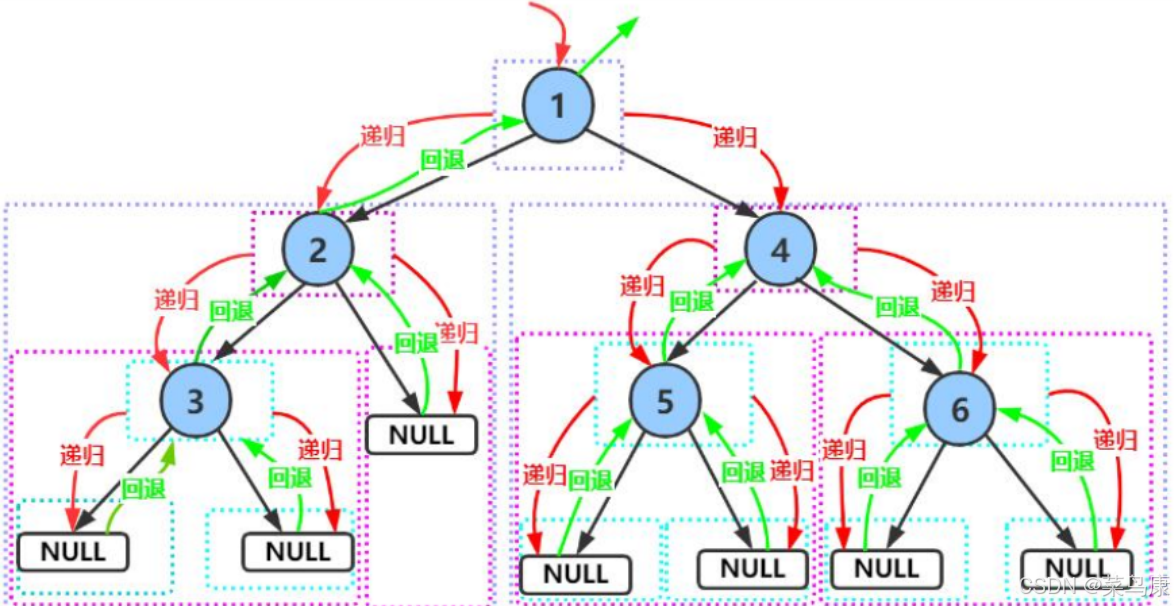
图的深度优先遍历基本思想:
- 从起始节点开始。
- 沿着当前节点的一个未被访问的邻接节点继续深入。
- 如果当前节点没有未被访问的邻接节点,则回溯(backtrack)到上一个节点。
- 直到所有节点都被访问过或者找到目标节点为止。
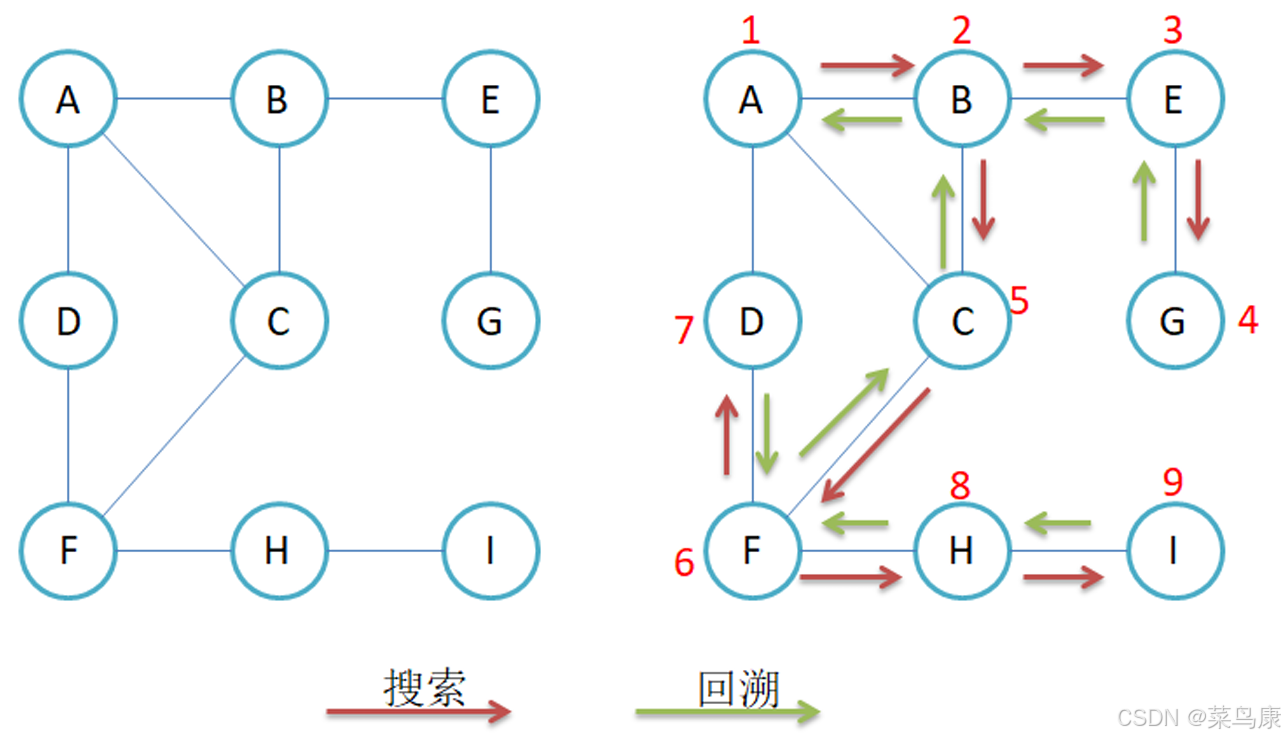
起点是A,那就从A开始,A遍历完,找一个与它直接相连的且没被遍历过的(这里如同广度优先遍历一样,同样需要对已经遍历过的点进行标识),那我们这里用的图结构是邻接矩阵的话,他找相连顶点的时候肯定就是按照那个结点对应的下标从小到大去找嘛。 那A找到的是B,然后B再去找一个与它邻接的顶点遍历(广度的话B遍历完就是继续找其它与A邻接的遍历),那B找到了E,那后面同样的,E再去找,找到G,再往后找发现没有了,开始回溯到E,E也找完了,回溯到B,B此时还有相邻的C没有找,于是到C.....直到找到某一个顶点它的所有邻接顶点都被遍历过了,然后往回退,再去走其它没有走过的路径去遍历 。
代码实现,图的深度优先遍历可以使用递归或者栈来实现,这里我们采用简单的方式:递归来实现
cpp
void _DFS(size_t srci, vector<bool>& visited)//当前要访问的顶点和记录是否是否被访问的数组
{
cout << srci << ":" << _vertexs[srci] << endl;
visited[srci] = true;
// 找一个srci相邻的没有访问过的点,去往深度遍历
for (size_t i = 0; i < _vertexs.size(); ++i)
{
if (_matrix[srci][i] != MAX_W && visited[i] == false)
{
_DFS(i, visited);
}
}
}
void DFS(const V& src)
{
size_t srci = GetVertexIndex(src);
vector<bool> visited(_vertexs.size(), false);
_DFS(srci, visited);
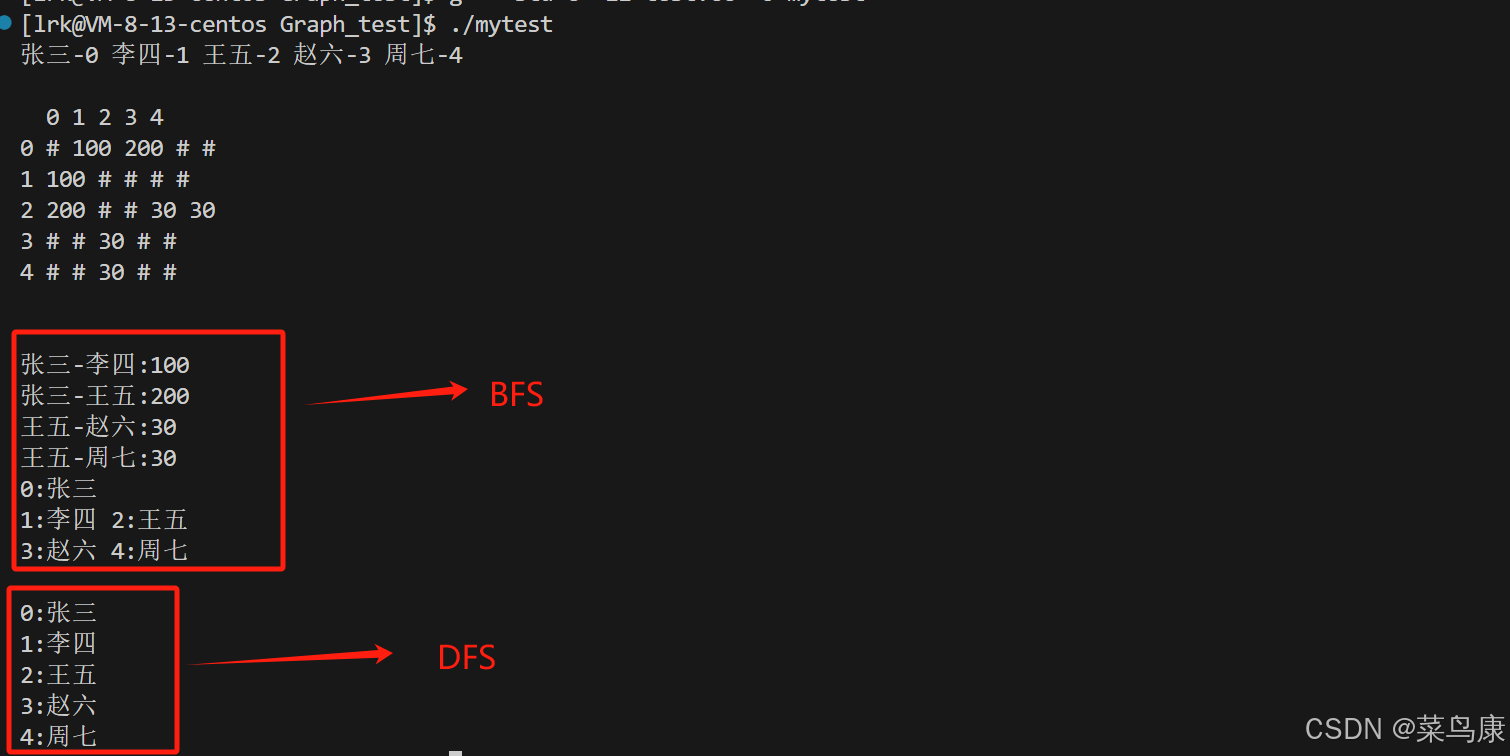
}运行结果,我们给出如下图

3、非连通图的情况:
上面给出的优先遍历方式都是基于图是连通图的情况,它可以由任意一点开始遍历完图中的所有的点,但是如果对于非连通图的情况呢?如下图所示
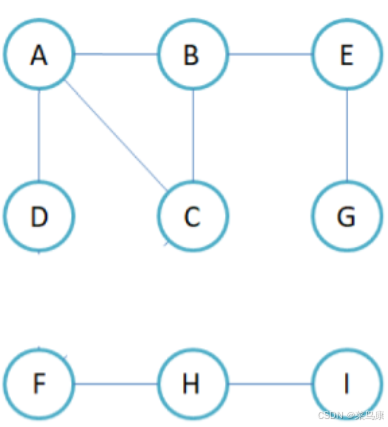
对于这种非连通图,如果我们再用上面的代码进行遍历的话,任取一个结点作为起点,比如还是A 那最终的结果就是我们只能遍历到上面的6个结点,最终遍历结束,还剩下面的3个结点我们是遍历不到的,因为它们跟上面的不连通,根本走不下来。
我们可以再在搞一个循环,每遍历一次之后,我们就去那个标记数组里面看还有没有没被遍历到的顶点,如果有的话,就再取一个没被遍历到的点作为起点,再进行对应的DFS/BFS遍历。 直到标记数组里面所有的位置都变成true,那就证明所有的顶点都被遍历过了。 这样对于非连通图我们也可以遍历完所有的顶点了。
cpp
//BFS
void BFS(const V& src)
{
size_t srci = GetVertexIndex(src);
vector<bool> visited(_vertexs.size(), false);
// 首先从指定起点开始BFS
_BFS(srci, visited);
// 检查是否有未访问的顶点(处理非连通图的情况)
for (size_t i = 0; i < _vertexs.size(); ++i)
{
if (!visited[i])
{
cout << "\nFound new component starting at: "
<< i << ":" << _vertexs[i] << endl;
_BFS(i, visited);
}
}
}
// 将原有BFS逻辑提取为辅助函数
void _BFS(size_t srci, vector<bool>& visited)
{
queue<size_t> q;
q.push(srci);
visited[srci] = true;
int levelSize = 1;
while (!q.empty())
{
// 一层一层出
for (int i = 0; i < levelSize; ++i)
{
size_t front = q.front();
q.pop();
cout << front << ":" << _vertexs[front] << " ";
// 把front顶点的邻接顶点入队列
for (size_t i = 0; i < _vertexs.size(); ++i)
{
if (_matrix[front][i] != MAX_W && !visited[i])
{
q.push(i);
visited[i] = true;
}
}
}
cout << endl;
levelSize = q.size();
}
}
cpp
//DFS
void _DFS(size_t srci, vector<bool>& visited, int depth = 0)
{
// 缩进显示递归深度
for (int i = 0; i < depth; ++i) cout << " ";
cout << srci << ":" << _vertexs[srci] << endl;
visited[srci] = true;
for (size_t i = 0; i < _vertexs.size(); ++i)
{
if (_matrix[srci][i] != MAX_W && !visited[i])
{
_DFS(i, visited, depth + 1);
}
}
}
void DFSTraverse()
{
vector<bool> visited(_vertexs.size(), false);
int componentCount = 0;
for (size_t i = 0; i < _vertexs.size(); ++i)
{
if (!visited[i])
{
cout << "Component " << ++componentCount << ":" << endl;
_DFS(i, visited);
}
}
cout << "Total components: " << componentCount << endl;
}感谢阅读!