剑指offer-19、顺时针打印矩阵

题⽬描述

输⼊⼀个矩阵，按照从外向⾥以顺时针的顺序依次打印出每⼀个数字，例如，如果输⼊如下4 X 4 矩阵：

则依次打印出数字 1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10 .

思路及解答

边界收缩法（推荐）

我们使⽤的是不断缩⼩矩阵上，下，左，右四个边界的⽅法。⾸先定义⼀个up （上边界为0 ）, down (下边界为matrix.length - 1 )， left （左边界为0 ）， right （右边界为matrix[0].length - 1 ）。

从第⼀个⾏第⼀个开始打印，向左边界遍历到右边界，之后将上边界加上1 （因为已经遍历完成上边界⼀⾏），判断上边界加上⼀之后是否⼤于下边界，如果是则调出。

之后执⾏类型操作，从上到下，从右到左，从下到上。

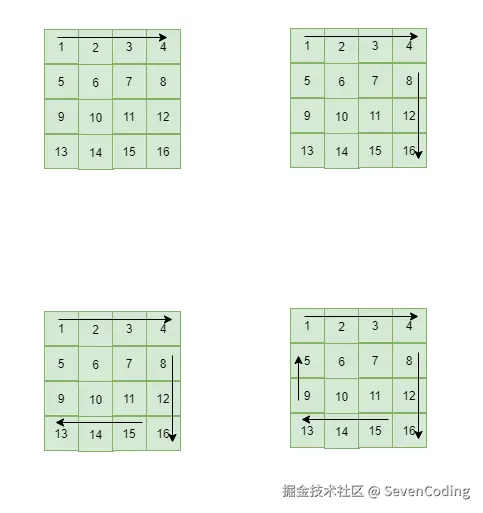
具体思路如下：

定义四个边界：上(up)、下(down)、左(left)、右(right)
按照顺时针方向遍历当前层：
- 从左到右遍历上边界
- 从上到下遍历右边界
- 从右到左遍历下边界
- 从下到上遍历左边界
遍历完一层后，收缩边界进入下一层

java 复制代码

public class Solution {
    public ArrayList<Integer> printMatrix(int[][] matrix) {
        ArrayList<Integer> results = new ArrayList();
        
        if (matrix != null && matrix.length > 0) {
            int left = 0;
            int right = matrix[0].length - 1;
            int up = 0;
            int down = matrix.length - 1;
            int i;
            while (true) {
                for (i = left; i <= right; i++) {
                    results.add(matrix[up][i]);
                }
                if ((++up) > down) {
                    break;
                }
                for (i = up; i <= down; i++) {
                    results.add(matrix[i][right]);
                }
                if (--right < left) {
                    break;
                }
                for(i=right;i>=left;i--){
                    results.add(matrix[down][i]);
                }
                if(--down<up){
                    break;
                }
                for(i=down;i>=up;i--){
                    results.add(matrix[i][left]);
                }
                if(++left>right){
                    break;
                }
            }
        }
    	return results;
    }
}

注意： (++up) > down 代表 up=up+1;up>dowm 两个语句。

时间复杂度：O(mn)，每个元素被访问一次
空间复杂度：O(1)，除了输出结果外只使用了固定数量的变量

方向模拟法

模拟顺时针移动的路径，按照右→下→左→上的方向顺序遍历：

定义四个方向向量表示移动方向
使用一个二维数组记录已访问的位置
当遇到边界或已访问的位置时，顺时针旋转方向

java 复制代码

public List<Integer> printMatrix(int[][] matrix) {
    List<Integer> result = new ArrayList<>();
    if (matrix == null || matrix.length == 0) return result;
    
    int rows = matrix.length, cols = matrix[0].length;
    boolean[][] visited = new boolean[rows][cols];
    int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    int directionIndex = 0;
    int row = 0, col = 0;
    
    for (int i = 0; i < rows * cols; i++) {
        result.add(matrix[row][col]);
        visited[row][col] = true;
        
        int nextRow = row + directions[directionIndex][0];
        int nextCol = col + directions[directionIndex][1];
        
        if (nextRow < 0 || nextRow >= rows || nextCol < 0 || nextCol >= cols 
            || visited[nextRow][nextCol]) {
            directionIndex = (directionIndex + 1) % 4;
        }
        
        row += directions[directionIndex][0];
        col += directions[directionIndex][1];
    }
    return result;
}

时间复杂度：O(mn)
空间复杂度：O(mn)，需要额外的visited数组

递归分解法

将矩阵分解为外层和内层，递归处理：

遍历当前矩阵的最外层
将剩余部分作为新矩阵递归处理
递归终止条件：矩阵为空或只剩一行/一列

java 复制代码

public List<Integer> printMatrix(int[][] matrix) {
    List<Integer> result = new ArrayList<>();
    if (matrix == null || matrix.length == 0) return result;
    spiralHelper(matrix, 0, matrix.length - 1, 0, matrix[0].length - 1, result);
    return result;
}

private void spiralHelper(int[][] matrix, int top, int bottom, int left, int right, List<Integer> result) {
    if (left > right || top > bottom) return;
    
    // 遍历上边
    for (int i = left; i <= right; i++) {
        result.add(matrix[top][i]);
    }
    
    // 遍历右边
    for (int i = top + 1; i <= bottom; i++) {
        result.add(matrix[i][right]);
    }
    
    if (top < bottom && left < right) { // 防止单行或单列
        // 遍历下边
        for (int i = right - 1; i >= left; i--) {
            result.add(matrix[bottom][i]);
        }
        
        // 遍历左边
        for (int i = bottom - 1; i > top; i--) {
            result.add(matrix[i][left]);
        }
    }
    
    // 递归处理内层
    spiralHelper(matrix, top + 1, bottom - 1, left + 1, right - 1, result);
}

时间复杂度：O(mn)
空间复杂度：O(min(m,n))，递归栈的深度