“鱼书”深度学习进阶笔记（1）第二章

最近在看斋藤康毅的《深度学习进阶：自然语言处理》，以下按章节做一点笔记。

这本书是《深度学习入门：基于Python的理论与实现》的续作，针对自然语言处理和时序数据处理 。如对"鱼书"第一本的笔记感兴趣，可看我之前做的笔记。

进阶版"鱼书"的封面如下：

01 第二章：自然语言和单词的分布式表达

自然语言处理，即让计算机理解人类语言的技术。

1.1 同义词词典

同义词词典，是人工定义单词含义。

在同义词词典中，具有相同含义的单词（同义词）或含义类似的单词（近义词）被归类到同一个组中。

如car的同义词有automobile、motorcar等。

在同义词词典有时还会定义单词之间更细的关系，如"上位-下位"，"整体-部分"等关系。

如下图：

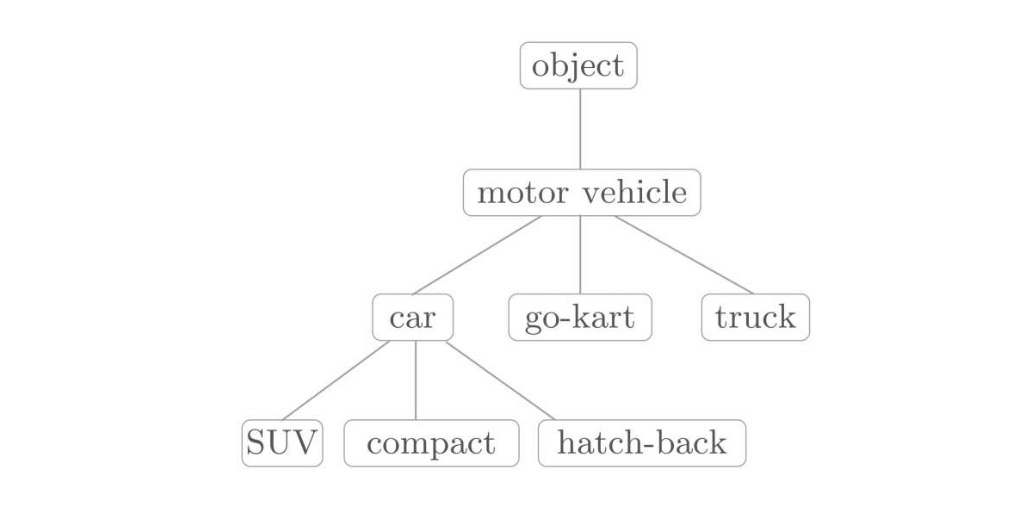
像这样，通过对所有单词创建近义词集合，并用图表示各个单词的关系，可以定义单词之间的联系。

利用这个"单词网络"，可以教会计算机单词之间的相关性。

1.1.1 WordNet

在自然语言处理领域，最著名的同义词词典是WordNet。

使用WordNet，可以获得单词的近义词，或者利用单词网络。 使用单词网络，可以计算单词之间的相似度。

附录B，使用WordNet来计算单词之间的相似度。（感兴趣可去了解）

1.1.2 同义词词典的问题

因为同义词词库是人工标记的，存在一些问题：

1. 词库需要及时更新；
2. 人力整理成本高；
3. 难以表示单词的微妙差异

目前，正在从人工制作词典或设计特征量的旧范式，向尽量减少人为干预的、仅从文本数据中获取最终结果的新范式转移。

1.2 基于计数的方法

1.2.1 语料库

语料库是大量的文本数据，一般收集的都是用于自然语言处理研究和应用的文本数据。

比如，语料库中包含了大量的关于自然语言的实践知识，即文章的写作方法、单词的选择方法和单词含义等。

基于计数的方法的目标就是从语料库中，自动且高效地提取本质。

为了方便计算机处理，语料库通常会被结构化（比如，采用树结构等数据形式）。

1.2.2 基于python的语料库的预处理

有各种语料库，如Wikipedia和Google News等。

另外，莎士比亚、夏目漱石等伟大作家的作品集也会被用作语料库。

这节所说的预处理是指，将文本分割为单词（分词），并将分割后的单词列表转化为单词ID列表。

作为语料库的样本文章（这里，使用由单个句子构成的文本作为语料库）：

text = 'You say goodbye and I say hello.'

实际使用的文本（text）应该包含成千上万个（连续的）句子。

python使用交互模式：

>>> text = text.lower() # lower（）将所有字母转化为小写（为了将句子开头的单词也作为常规单词处理）
>>> text = text.replace('.' , ' .') # 在句子结尾处加了个空格
>>> text
'you say goodbye and i say hello .'

>>> words = text.split(' ') # 用空格作为分隔符，进行句子切分
>>> words
['you', 'say', 'goodbye', 'and', 'i', 'say', 'hello', '.']

上面的代码是使用空格进行分词，也可使用正则表达式。通过导入正则表达式的re模块，使用re.split（'（\W+）?', text）也可以进行分词。

接着，我们需要对单词标上id，以便使用单词id列表。

使用python的字典来创建单词id和单词的对应表。

>>> word to id = {}
>>> id to word = {}
>>>
>>> for word in words :  # 开始遍历words列表中的每个单词
...      if word not in word to id:
...          new id = len(word to id) # 使用当前字典的长度作为新id
...          word to id[word] = new id  # 将单词映射到id（就是单词和id联系起来）
...          id to word[new id] = word  # 将id映射回单词

变量id_to_word负责将单词ID转化为单词（键是单词ID，值是单词）, word_to_id负责将单词转化为单词ID。

如果单词不在word_to_id中，则分别向word_to_id和id_to_word添加新ID和单词。另外，我们将字典的长度设为新的单词ID，单词ID按0, 1, 2,···逐渐增加。

这样就创建好了单词id和单词的对应表：

>>> id to word
{0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6:'.'}
>>> word to id
{'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5, '.': 6}

此时可以根据单词检索单词id，也可以用单词id检索单词。

例如：

​​​​​​​​​​>>> id to word[1]​​        
'say'
​​​​​​​​>>> word to id['hello']​​        
5​​

接着，将单词列表转变为单词id列表：

>>> import numpy as np
>>> corpus = [word to id[w] for w in words]​​  # 遍历words中的每个单词；对于每个单词，在word to id的字典里查找对应id，并将单词的id组成一个新的列表corpus
>>> corpus = np.array(corpus)​​        
>>>> corpus​​        
array（[0, 1, 2, 3, 4, 1, 5, 6]）​​

将前面实现的内容，包装为preprocess（）函数实现：

def preprocess(text):
    text = text.lower()
    text = text.replace('.', ' .')
    words = text.split(' ')

    word_to_id = {}
    id_to_word = {}
    for word in words:
       if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])

    return corpus, word_to_id, id_to_word  # corpus是单词ID列表，word_to_id是单词到单词ID的字典，id_to_word是单词ID到单词的字典。

1.2.3 单词的分布式表示

我们期望将单词表示为向量，这样会更容易判断和量化。

准备把握单词含义的向量表示，称为分布式表示。

单词的分布式表示将单词表示为固定长度的向量。

这种向量的特征在于它是用密集向量表示的。

密集向量的意思是，向量的各个元素（大多数）是由非0实数表示的。

1.2.4 分布式假设

分布式假设：即某个单词的含义由它周围的单词形成。

分布式假设的理念是：单词本身没有含义，单词含义由它所在的上下文（语境）形成。

本章说的上下文是指某个单词（关注词）周围的单词。

将上下文的大小（即周围的单词有多少个）称为窗口大小（window size）

如下图，窗口大小为2的上下文例子。在关注goodbye时，将其左右各2个单词用作上下文

1.2.5 共现矩阵

如何给予分布式假设使用向量表示单词？

最基本的实现方法是对周围单词的数量进行技术。

即，在关注某个单词的情况下，对它的周围出现了多少次什么单词进行计数，然后再汇总。这里，我们将这种做法称为"基于计数的方法"，在有的文献中也称为"基于统计的方法。

基于前面写的preprocess（）函数，接着编写如下代码：

​​​​​​​text = 'You say goodbye and I say hello.'
​​​​​​​​corpus, word_to_id, id_to_word = preprocess(text)

​​​​​​​​print (corpus)
​​​​​​​​# [0 1 2 3 4 1 5 6]

​​​​​​​​print (id_to_word)
​​​​​​​​# {0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6:'.'}

接着，我们计算每个单词的上下文所包含单词的频数。

将窗口大小设为1，从单词id=0的you开始，单词you的上下文仅有say这个单词。

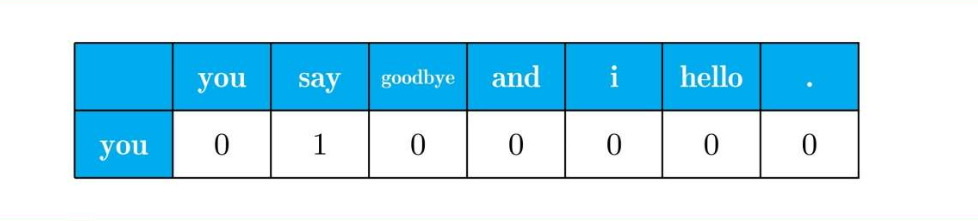
接着对say进行分析：

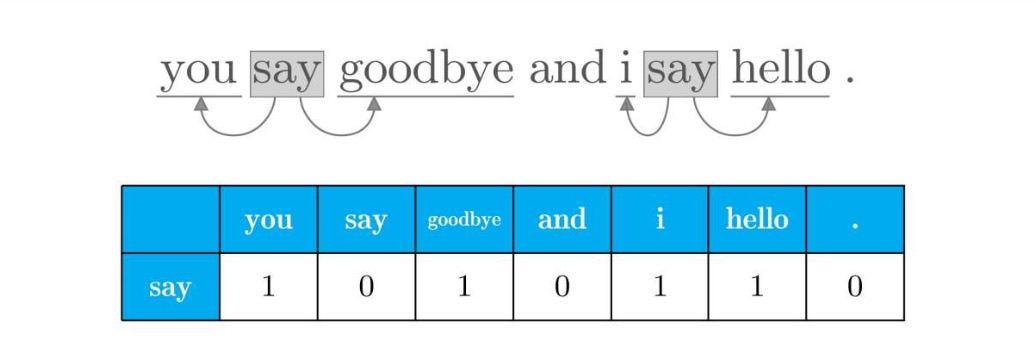
依次对其他词进行分析，得到表格：

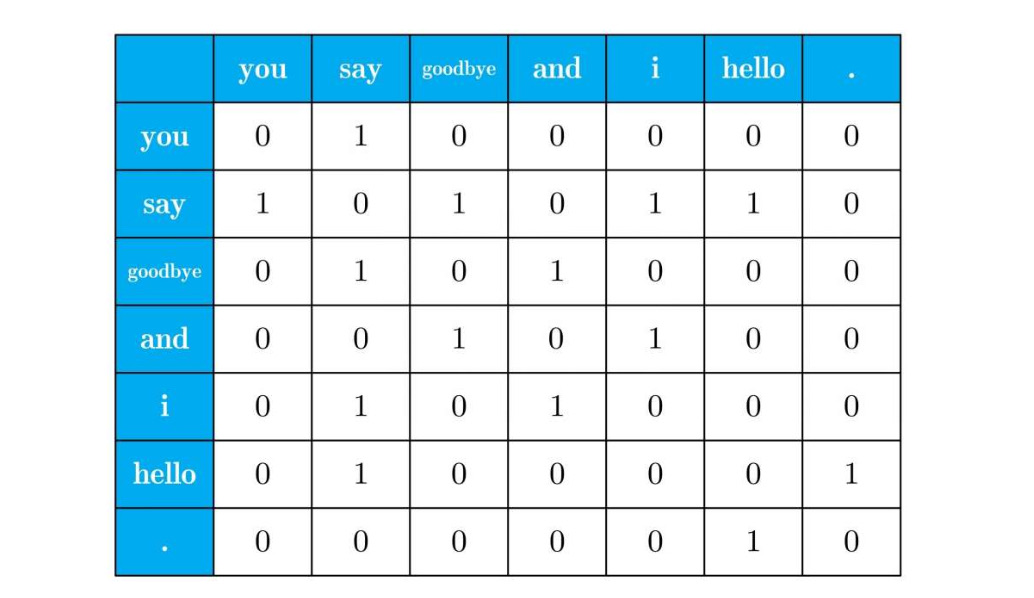
这个表格的各行对应相应单词的向量。

因上面的表格呈矩阵状，被称为共现矩阵。

创建一下上面的共现矩阵：

 C = np.array([
      [0, 1, 0, 0, 0, 0, 0],
​​​​​​​​      [1, 0, 1, 0, 1, 1, 0],
​​​​​​​​      [0, 1, 0, 1, 0, 0, 0],
​​​​​​​​      [0, 0, 1, 0, 1, 0, 0],
​​​​​​​​      [0, 1, 0, 1, 0, 0, 0],
​​​​​​​​      [0, 1, 0, 0, 0, 0, 1],
​​​​​​​​      [0, 0, 0, 0, 0, 1, 0],
​​​​​​​​  ], dtype=np.int32)

即为共现矩阵。

使用这个共现矩阵，可以获得各个单词的向量。如：

print (C[0]) # 单词ID为0的向量
​​​​​​​​# [0 1 0 0 0 0 0]

​​​​​​​​print (C[4]) # 单词ID为4的向量
​​​​​​​​# [0 1 0 1 0 0 0]

​​​​​​​​print (C[word_to_id['goodbye']]) # goodbye的向量
​​​​​​​​# [0 1 0 1 0 0 0]​​

我们不可能每次都人为输入矩阵。

这里，我们创建一个函数create_co_matrix（corpus, vocab_size, window_size=1），能够直接从语料库生成共现矩阵。

其中参数corpus是单词ID列表，参数vocab_size是词汇个数，window_size是窗口大小：

def create_co_matrix(corpus, vocab_size, window_size=1):
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size,vocab_size),dtype=np.int32) # 创建0矩阵

    for idx, word_id in enumerate(corpus):  # 使用enumerate获取每个单词的索引idx和对应的单词id，对语料中的每个单词进行处理
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0: # 确保左侧索引不小于0（避免负索引）
                left_word_id = corpus[left_idx] # 获取左侧邻居索引单词的id
                co_matrix[word_id, left_word_id] += 1

            if right_idx < corpus_size:  # 对右侧索引的思考
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1

    return co_matrix

1.2.6 向量间的相似度

测量向量间的相似度有很多方法，其中具有代表性的方法有向量内积或欧式距离等。

在测量单词的向量表示的相似度方面，余弦相似度（cosine similarity）比较常用。

设有x=（x1, x2, x3,···, xn）和y=（y1, y2, y3,···, yn）两个向量，则它们的余弦相似度的定义为：

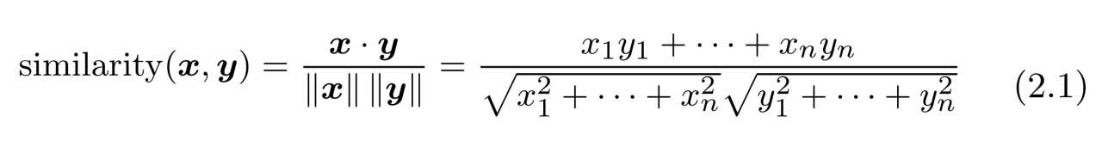
余弦相似度可以直观地表示了"两个向量在多大程度上指向同一方向"。

两个向量完全指向相同的方向时，余弦相似度为1；完全指向相反的方向时，余弦相似度为-1。

为避免"除数为0的错误"，会给一微小值eps，实现代码为：

def cos_similarity(x, y,eps=1e-8):
    nx = x / np.sqrt(np.sum(x**2)+eps) # x的正规化
    ny = y / np.sqrt(np.sum(y**2)+eps) # y的正规化
    return np.dot(nx, ny)

基于前面preprocess, create_co_matrix, cos_similarity函数，可以求得you和i的相似度：

text = 'You say goodbye and I say hello.'
​​​​​​​​corpus, word_to_id, id_to_word = preprocess(text)
​​​​​​​​vocab_size = len(word_to_id)
​​​​​​​​C = create_co_matrix(corpus, vocab_size)

​​​​​​​​c0 = C[word_to_id['you']]  # you的单词向量
​​​​​​​​c1 = C[word_to_id['i']]     # i的单词向量
​​​​​​​​print (cos_similarity(c0, c1))
​​​​​​​​# 0.7071067691154799​​

所以可以得倒you和i的余弦相似度数值，这个数值相对较高（存在相似性）。

1.2.7 相似单词的排序

我们下面想要实现另一个函数most_similar（）：当某个单词被作为查询词时，将与这个查询词相似的单词按降序显示出来。

参数设置如下：

def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
    # ❶取出查询词
    if query not in word_to_id:
        print('%s is not found' % query)
        return

    print('\n[query] ' + query)  # 打印查询词（前面加空行）
    query_id = word_to_id[query]  # 获取查询词的id
    query_vec = word_matrix[query_id]  # 获取查询词的词向量

    # ❷计算余弦相似度
    vocab_size = len(id_to_word)
    similarity = np.zeros(vocab_size)  # 初始化，用于存储相似度分数

    for i in range(vocab_size):
        similarity[i] = cos_similarity(word_matrix[i], query_vec)  # 计算查询词和每个词向量的余弦相似度

    # ❸基于余弦相似度，按降序输出值
    count = 0
    for i in (-1 * similarity).argsort():  # 通过乘以-1，将升序排序转为降序排列的索引
        if id_to_word[i] == query:
            continue  # 跳过查询词本身
        print(' %s: %s' % (id_to_word[i], similarity[i]))
        count += 1
        if count >= top:
            return

argsort()方法对数组的索引进行了重排，按升序对NumPy数组的元素进行排序（不过，返回值是数组的索引）。

下面是一个例子：

>> x = np.array([100 , -20 , 2])​​        
>>>> x.argsort()​​        
array([1, 2, 0])​​

上述代码对NumPy数组[100,-20, 2]的各个元素按升序进行了排列。

此时，返回的数组的各个元素对应原数组的索引。

上述结果的顺序是"第1个元素（-20）""第2个元素（2）""第0个元素（100）"。

现在我们想做的是将单词的相似度按降序排列，

因此，将NumPy数组的各个元素乘以-1后，再使用argsort（）方法，即most_similar（）函数中的实现方法。

这里将you作为查询词，基于前面的函数代码，进行相似度计算：

text = 'You say goodbye and I say hello.'
​​​​​​​​corpus, word_to_id, id_to_word = preprocess(text)
​​​​​​​​vocab_size = len(word_to_id)
​​​​​​​​C = create_co_matrix(corpus, vocab_size)
most_similar('you', word_to_id, id_to_word, C, top=5）)

执行的结果为：

[query] you
​​​​​​​​goodbye: 0.7071067691154799
​​​​​​​​i: 0.7071067691154799
​​​​​​​​hello: 0.7071067691154799
​​​​​​​​say: 0.0
​​​​​​​​and: 0.0​​

这个结果按降序显示了you这个查询词的前5个相似单词，各个单词旁边的值是余弦相似度。

观察上面的结果可知，和you最接近的单词有3个，分别是goodbye、i（=I）和hello。

i和you都是人称代词，二者相似可以理解。

但是，goodbye和hello的余弦相似度也很高。出现这种情况一个可能的原因是，这里的语料库太小了。

1.3 基于计数的方法的改进

1.3.1 点互信息

上一节的共现矩阵的元素表示两个单词同时出现的次数。

但是只是利用频率，这样会存在一些问题，给出例子：

比如，我们来考虑某个语料库中the和car共现的情况。在这种情况下，我们会看到很多"...the car..."这样的短语。因此，它们的共现次数将会很大。另外，car和drive也明显有很强的相关性。但是，如果只看单词的出现次数，那么与drive相比，the和car的相关性更强。这意味着，仅仅因为the是个常用词，它就被认为与car有很强的相关性。

这里引入点互信息 （Pointwise Mutual Information, PMI）。

对于随机变量x和y，定义为：

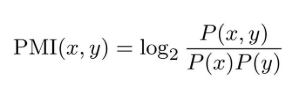
其中，P（x）表示x发生的概率，P（y）表示y发生的概率，P（x, y）表示x和y同时发生的概率。PMI的值越高，表明相关性越强。

使用共现矩阵（其元素表示单词共现的次数）来重写上面的公式。

这里，将共现矩阵表示为C，将单词x和y的共现次数表示为C（x, y）​，将单词x和y的出现次数分别表示为C（x）​、C（y）​，将语料库的单词数量记为N，则可重写为：

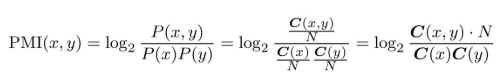
例子：这里假设语料库的单词数量（N）为10000,the出现100次，car出现20次， drive出现10次，the和car共现10次，car和drive共现5次。这时，如果从共现次数的角度来看，则与drive相比，the和car的相关性更强。

如果从PMI的角度：

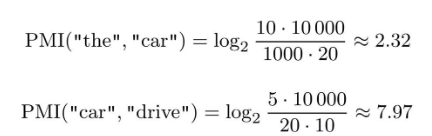
之所以出现这个结果，是因为我们考虑了单词单独出现的次数。

在这个例子中，因为the本身出现得多，所以PMI的得分被拉低了。

但PMI得计算也会存在问题：当两个单词的共现次数为0时，log0=-∞。

所以，引入正的点互信息（Positive PMI,PPMI）​：

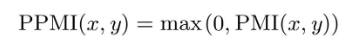
这样就可以将单词间的相关性表示为大于等于0的实数。

实现ppmi的代码为：

import numpy as np

def ppmi(C, verbose = False, eps = 1e-8):  # C：输入的共现矩阵（二维数组，通常是词与词之间的共现次数）
    M = np.zeros_like(C, dtype = np.float32)
    N = np.sum(C)  # N 是 C 矩阵中所有元素的总和（即所有共现次数的总和）
    S = np.sum(C, axis = 0)  # S 是每一列的和（列向量），表示每个词作为"目标词"时，与所有"上下文词"的总共现次数
    total = C.shape[0] * C.shape[1]  #total 是矩阵 C 的总元素个数（行数 × 列数）,可用来计算进度百分比
    cnt = 0

    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            pmi = np.log2(C[i, j] * N / (S[j] * S[i]) + eps)
            M[i, j] = max(0, pmi)

            if verbose:  # verbose：是否在计算过程中显示进度，默认 False
                cnt += 1
                if cnt % (total // 100+1) == 0:  # total // 100 + 1 确保分母不会为零
                    print ('%.1f%% done' % (100 * cnt / total))
    return M

检验代码：

text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
W = ppmi(C)

np.set_printoptions(precision = 3)  # 有效位数为3位
print ('covariance matrix')
print (C)
print ('-' * 50)
print ('PPMI')
print (W)

上面的输出为：

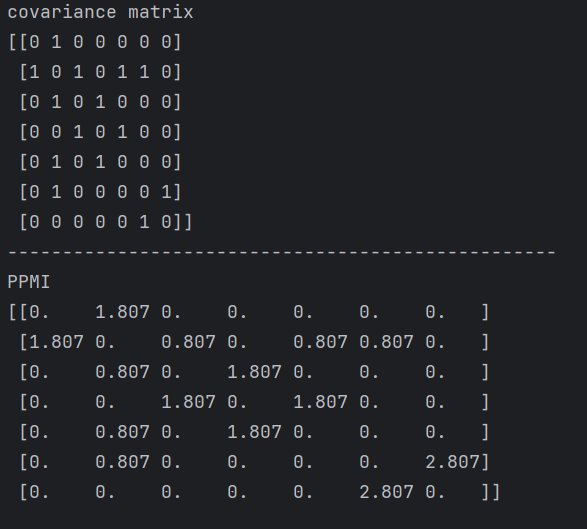
但ppmi还是存在一个问题：

随着语料库的词汇量增加，各个单词向量的维数也会增加。

如果语料库的词汇量达到10万，则单词向量的维数也同样会达到10万。处理10万维向量并不现实的。

这个矩阵中，很多元素为0，说明向量中的绝大多数并不重要。即，这部分元素的"重要性"较低。这样的向量也容易受到噪声影响，稳健性差。

对于这些问题，这里引入向量降维。

1.3.2 降维

降维（dimensionality reduction）​，就是减少向量维度。

但是，并不是简单地减少，而是在尽量保留"重要信息"的基础上减少。

向量中的大多数元素为0的矩阵（或向量）称为稀疏矩阵（或稀疏向量）​。

重点是，从稀疏向量中找出重要的轴，用更少的维度对其进行重新表示。

接着，将稀疏矩阵转化为大多数元素均不为0的密集矩阵。

这个密集矩阵就是我们想要的单词的分布式表示。

降维的方法很多，这里使用奇异值分解 （Singular Value Decomposition,SVD）​。

SVD将任意矩阵分解为3个矩阵的乘积：

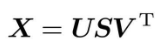
SVD将任意的矩阵X分解为U、S、V这3个矩阵的乘积，其中U和V是列向量彼此正交的正交矩阵，S是除了对角线元素以外其余元素均为0的对角矩阵。

变化关系为：

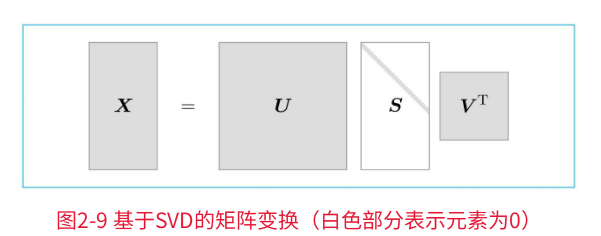
U是正交矩阵。这个正交矩阵构成了一些空间中的基轴（基向量）​，我们可以将矩阵U作为"单词空间"​。

S是对角矩阵，奇异值在对角线上降序排列。简单地说，我们可以将奇异值视为"对应的基轴"的重要性。

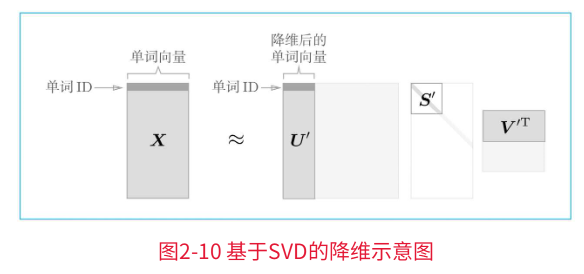
如上图，矩阵S的奇异值小，对应的基轴的重要性低，因此，可以通过去除矩阵U中的多余的列向量来近似原始矩阵。

1.3.3 基于SVD的降维

使用NumPy的linalg模块中的svd方法。

linalg是linear algebra（线性代数）的简称。

下面，创建一个共现矩阵，将其转化为PPMI矩阵，然后对其进行SVD ：

text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
W = ppmi(C)

U,S,V = np.linalg.svd(W)
print(C[0])  # 共现矩阵第一行（就是第 0 号单词与所有其他单词的共现次数向量）
print(W[0])  # ppmi矩阵第一行
print(U[0])  # SVD （U[0] 就是 第 0 号单词在降维前（或后你取部分列）的向量表示），经常取 U 的前 k 列作为低维词向量（word embedding

输出结果为：

原先的稀疏向量W[0]经过SVD被转化成了密集向量U[0]​。如果要对这个密集向量降维，比如把它降维到二维向量，取出前两个元素即可（因为U的输出是按重要性排序的）：

print(U[0,:2])

这样就完成了降维。

下面用二维向量表示各个单词：

U,S,V = np.linalg.svd(W)
for word, word_id in word_to_id.items():
    # 给一个点加文字标注，
    # (U[word_id, 0], U[word_id, 1])：这个单词在二维空间（SVD 的前两个方向）上的坐标；
    # word：显示的文字，就是单词本身
    plt.annotate(word, (U[word_id, 0], U[word_id, 1]))

plt.scatter(U[:, 0], U[:, 1], alpha = 0.5) # U[:, 0]：所有词在第 1 个奇异向量方向上的坐标（x 轴）；U[:, 1]：所有词在第 2 个奇异向量方向上的坐标（y 轴）；plt.scatter 把这些坐标画成散点图；alpha=0.5 让点半透明，方便看重叠的点
plt.show()

得到展示为：

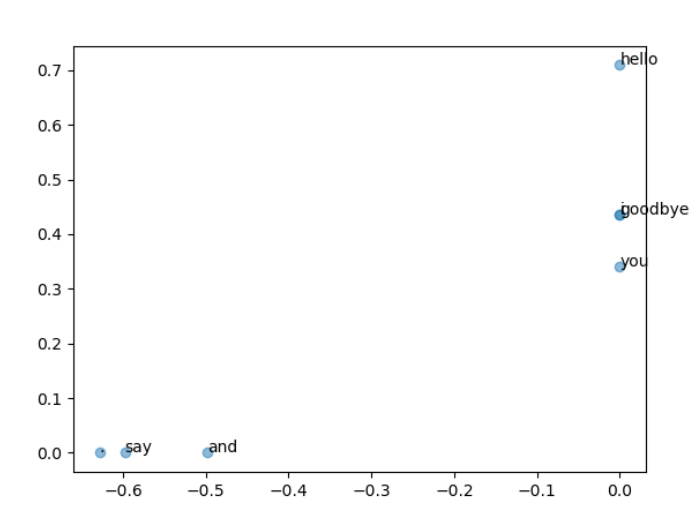
1.3.4 对于SVD降维的坐标的理解

上面代码里的降维后的坐标，本质上是 词在前两个主要语义方向上的投影值。

1. 坐标的来源：

   我们先有一个 PPMI 矩阵 W，它表示词和词之间的统计关联强度（越大代表两个词在上下文中一起出现的可能性越大）。

   np.linalg.svd(W) 会找到一组新的正交坐标轴（奇异向量方向），这些方向是：

   第 1 个方向（U[:, 0]）：数据中方差最大、信息量最多的方向

   第 2 个方向（U[:, 1]）：在第一个方向正交的情况下，方差第二大的方向

   所以 (U[word_id, 0], U[word_id, 1]) 就是 某个词在这两个最重要语义方向上的位置。

2. 语义上的意义

   如果两个词在原始高维空间（PPMI 矩阵的行）里很相似，比如它们经常出现在相似的上下文中，那么，它们在降维后的二维平面上也会 距离很近

   例如：

   "cat" 和 "dog" 出现在相似的句子环境中（都有 "pet", "animal" 等上下文），那么它们会被投影到二维平面上比较接近的点。

   "cat" 和 "car" 则可能在语义上差很远，所以二维平面上的距离也会很大。

3. 为什么要取前两个方向

   原始 PPMI 矩阵的维度等于词表大小，比如 10000 个词 → 每个词是 10000 维向量，没法直接画图。

   SVD 可以用很少的维度（比如 2 维）去近似原空间的结构，保留尽量多的语义信息。

   前两个方向是最"重要"的方向，相当于抓住了语义信息中变化最大的部分。

4. 降维后的 (x, y) 坐标表示：这个词在两个最主要的语义变化方向上的"分数"

   距离近 → 语义相似

   距离远 → 语义差异大

   （即坐标数值本身没有意义，真正有意义的是 不同词之间的相对位置）

1.3.5 PTB 数据集

如果矩阵大小是N，SVD需要与N的立方成比例的计算量。

现实中这样的计算量是做不到的，所以往往会使用Truncated SVD等更快的方法。

Truncated SVD通过截去（truncated）奇异值较小的部分，从而实现高速化。

之前，使用的是非常小的文本数据作为语料库。

接下来将使用一个大小合适的"真正的"语料库---Penn Treebank语料库（以下简称为PTB）​。

关于PTB的一些基本介绍：

使用代码为：

# 开始用PTB的库
import sys
import os
sys.path.append('..')
try:
    import urllib.request
except ImportError:
    raise ImportError('Use Python3!')
import pickle
import numpy as np


url_base = 'https://raw.githubusercontent.com/tomsercu/lstm/master/data/'
key_file = {
    'train':'ptb.train.txt',
    'test':'ptb.test.txt',
    'valid':'ptb.valid.txt'
}
save_file = {
    'train':'ptb.train.npy',
    'test':'ptb.test.npy',
    'valid':'ptb.valid.npy'
}
vocab_file = 'ptb.vocab.pkl'
dataset_dir = os.path.dirname(os.path.abspath(__file__))

def _download(file_name):
    file_path = dataset_dir + '/' + file_name
    if os.path.exists(file_path):
        return

    print('Downloading ' + file_name + ' ... ')

    try:
        urllib.request.urlretrieve(url_base + file_name, file_path)
    except urllib.error.URLError:
        import ssl
        ssl._create_default_https_context = ssl._create_unverified_context
        urllib.request.urlretrieve(url_base + file_name, file_path)

    print('Done')

def load_vocab():
    vocab_path = dataset_dir + '/' + vocab_file

    if os.path.exists(vocab_path):
        with open(vocab_path, 'rb') as f:
            word_to_id, id_to_word = pickle.load(f)
        return word_to_id, id_to_word

    word_to_id = {}
    id_to_word = {}
    data_type = 'train'
    file_name = key_file[data_type]
    file_path = dataset_dir + '/' + file_name

    _download(file_name)

    words = open(file_path).read().replace('\n', '<eos>').strip().split()

    for i, word in enumerate(words):
        if word not in word_to_id:
            tmp_id = len(word_to_id)
            word_to_id[word] = tmp_id
            id_to_word[tmp_id] = word

    with open(vocab_path, 'wb') as f:
        pickle.dump((word_to_id, id_to_word), f)

    return word_to_id, id_to_word

def load_data(data_type='train'):
    '''
        :param data_type: 数据的种类：'train' or 'test' or 'valid (val)'
        :return:
    '''
    if data_type == 'val': data_type = 'valid'
    save_path = dataset_dir + '/' + save_file[data_type]

    word_to_id, id_to_word = load_vocab()

    if os.path.exists(save_path):
        corpus = np.load(save_path)
        return corpus, word_to_id, id_to_word

    file_name = key_file[data_type]
    file_path = dataset_dir + '/' + file_name
    _download(file_name)

    words = open(file_path).read().replace('\n', '<eos>').strip().split()
    corpus = np.array([word_to_id[w] for w in words])

    np.save(save_path, corpus)
    return corpus, word_to_id, id_to_word


corpus, word_to_id, id_to_word = load_data('train')

print('corpus size:', len(corpus))
print('corpus[:30]:', corpus[:30])
print()
print('id_to_word[0]:', id_to_word[0])
print('id_to_word[1]:', id_to_word[1])
print('id_to_word[2]:', id_to_word[2])
print()
print("word_to_id['car']:", word_to_id['car'])
print("word_to_id['happy']:", word_to_id['happy'])
print("word_to_id['lexus']:", word_to_id['lexus'])

后部分代码是语料库的使用，和之前的用法基本一样。corpus中保存了单词ID列表，id_to_word是将单词ID转化为单词的字典，word_to_id是将单词转化为单词ID的字典。

输出为：

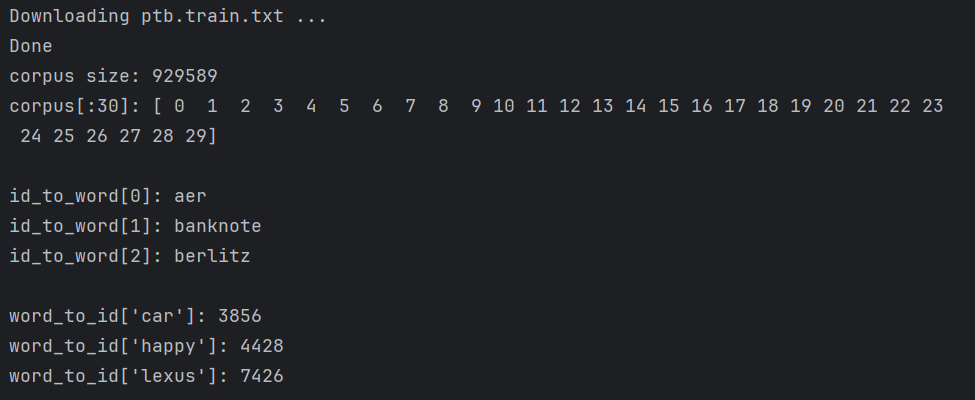
1.3.6 基于PTB数据集的评价

前面是基本版的SVD（np.linalg.svd（​）​）​，尝试使用更快速的SVD，需要安装sklearn模块。

执行代码为：

window_size = 2  # 设置共现矩阵的窗口大小，表示一个单词和前后 2 个单词 都会被认为是上下文
wordvec_size = 100  # 设置最终降维后的词向量维度为 100

corpus, word_to_id, id_to_word = load_data('train')
vocab_size = len(word_to_id)  # 获取词汇表的大小（总共有多少个唯一单词）
print('counting  co-occurrence ...')
C = create_co_matrix(corpus, vocab_size, window_size)
print('calculating PPMI ...')
W = ppmi(C, verbose=True)

print('calculating SVD ...')
try:
    # truncated SVD (fast!)
    from sklearn.utils.extmath import randomized_svd
    U, S, V = randomized_svd(W, n_components=wordvec_size, n_iter=5,
                             random_state=None) # 代表不固定随机数种子，每次运行会生成不同的随机投影矩阵，因此结果可能稍有差异
except ImportError:
    # SVD (slow)
    U, S, V = np.linalg.svd(W)

word_vecs = U[:, :wordvec_size]

querys = ['you', 'year', 'car', 'toyota']
for query in querys:
    most_similar(query, word_to_id, id_to_word, word_vecs, top=5)

输出结果为：

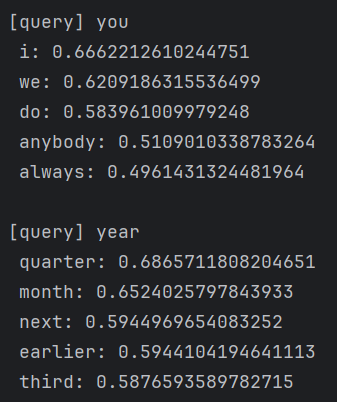
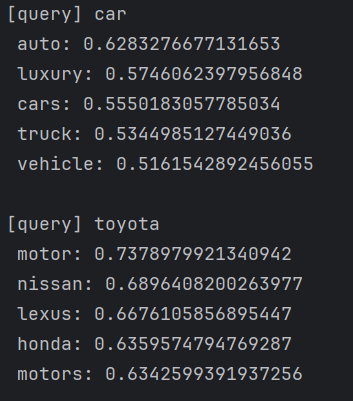
得到了，在含义或语法上相似的单词表示为相近的向量，符合我们预期。