深度学习之张量

目录

一、Tensor基础

概念

特点

数据类型

二、Tensor张量的创建

基本创建方式

torch.tensor

torch.Tensor

torch.IntTensor

线性张量

随机张量

随机数种子

随机张量

三、Tensor常见属性

获取属性

切换设备

类型转换

四、Tensor数据转换

Tensor与Numpy

张量转numpy

numpy转张量

五、Tensor常见操作

获取元素值

阿达玛积

Tensor相乘

形状操作

reshape

view

内存连续性

view变形操作

transpose

permute

变维

降维

升维

广播机制

六、自动微分

计算梯度

标量梯度计算

向量梯度计算

多标量梯度计算

多向量梯度计算

梯度上下文控制

控制梯度计算

累计梯度

梯度清零

总结

---

一、Tensor基础

概念

张量是一个多维数组，通俗来说可以看作是扩展了标量、向量、矩阵的更高维度的数组。张量的维度决定了它的形状（Shape），例如：

• 标量 是 0 维张量，如 a = torch.tensor(5)

• 向量 是 1 维张量，如 b = torch.tensor([1, 2, 3])

• 矩阵 是 2 维张量，如 c = torch.tensor([[1, 2], [3, 4]])

• 更高维度的张量，如3维、4维等，通常用于表示图像、视频数据等复杂结构。

特点

动态计算图：PyTorch 支持动态计算图，这意味着在每一次前向传播时，计算图是即时创建的。

GPU 支持 ：PyTorch 张量可以通过 .to('cuda') 移动到 GPU 上进行加速计算。

自动微分 ：通过 autograd 模块，PyTorch 可以自动计算张量运算的梯度，这对深度学习中的反向传播算法非常重要。

数据类型

PyTorch中有3种数据类型：浮点数、整数、布尔。其中，浮点数和整数又分为8位、16位、32位、64位，加起来共9种。

为什么要分为8位、16位、32位、64位呢？
场景不同，对数据的精度和速度要求不同。通常，移动或嵌入式设备追求速度，对精度要求相对低一些。精度越高，往往效果也越好，自然硬件开销就比较高。

二、Tensor张量的创建

基本创建方式

torch.tensor

这里的tensor是小写，是根据指定的数据创建张量。

import torch
import numpy as np

def test1():
    # 1.用标量创建张量
    tensor = torch.tensor(5)
    print(tensor.shape)

    # 2.使用numpy随机一个数组创建张量
    tensor = torch.tensor(np.random.randn(3, 5))
    print(tensor)
    print(tensor.shape)

    # 3.根据list创建tensor
    tensor = torch.tensor([[1, 2, 3], [4, 5, 6]])
    print(tensor)
    print(tensor.shape)
    print(tensor.dtype)

# 调用函数方法
if __name__ == '__main__':
    test1()

如果出现如下错误：

UserWarning: Failed to initialize NumPy: _ARRAY_API not found

一般是因为numpy和pytorch版本不兼容，可以选择降低numpy版本

torch.Tensor

这里的Tensor是大写，根据形状 创建张量，也可用来创建指定数据的张量。

import torch
import numpy as np

def test2():
    # 1.根据形状创建张量
    tensor1 = torch.Tensor(2, 3)
    print(tensor1)

    # 2.也可以是具体的值
    tensor2 = torch.Tensor([[1, 2, 3], [4, 5, 6]])
    print(tensor2, tensor2.shape, tensor2.dtype)

    tensor3 = torch.Tensor([10])
    print(tensor3, tensor3.shape, tensor3.dtype)
    
    # 指定tensor数据类型
    tensor1 = torch.Tensor([1,2,3]).short()
    print(tensor1)
    
    tensor1 = torch.Tensor([1,2,3]).int()
    print(tensor1)
    
    tensor1 = torch.Tensor([1,2,3]).float()
    print(tensor1)
    
    tensor1 = torch.Tensor([1,2,3]).double()
    print(tensor1)

if __name__ == "__main__":
    test2()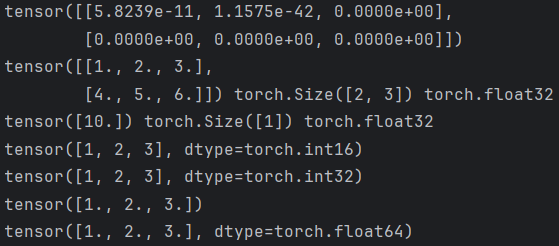

torch.Tensor与torch.tensor区别

特性	torch.Tensor()	torch.tensor()
数据类型推断	强制转为 torch.float32	根据输入数据自动推断（如整数→int64）
显式指定 dtype	不支持	支持（如 dtype=torch.float64）
设备指定	不支持	支持（如 device='cuda'）
输入为张量时的行为	创建新副本（不继承原属性）	默认共享数据（除非 copy=True）
推荐使用场景	需要快速创建浮点张量	需要精确控制数据类型或设备

torch.IntTensor

用于创建指定类型的张量，还有诸如Torch.FloatTensor、 torch.DoubleTensor、 torch.LongTensor......等。

如果数据类型不匹配，那么在创建的过程中会进行类型转换，要尽可能避免，防止数据丢失。

import torch

def test3():
    # 创建指定形状的张量
    t1 = torch.IntTensor(2, 3)
    print(t1)

    t2 = torch.FloatTensor(3, 3)
    print(t2, t2.dtype)
    t3 = torch.DoubleTensor(3, 3)
    print(t3, t3.dtype)
    t4 = torch.LongTensor(3, 3)
    print(t4, t4.dtype)
    t5 = torch.ShortTensor(3, 3)
    print(t5, t5.dtype)

if __name__ == "__main__":
    test3()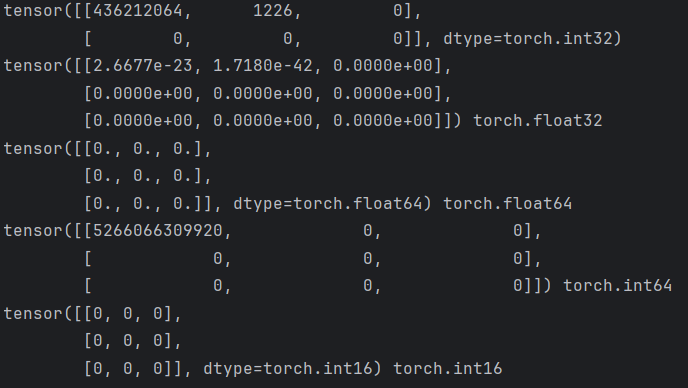

线性张量

使用torch.arange 和 torch.linspace 创建线性张量：

import torch
import numpy as np

# 不用科学计数法打印
torch.set_printoptions(sci_mode=False)

def test4():
    # 1.创建线性张量
    r1 = torch.arange(0, 10, 2)
    print(r1)
    # 2.在指定空间按照元素个数生成张量：等差
    
    r2 = torch.linspace(3, 10, 10)   # star  end  step
    print(r2)
    
    r2 = torch.linspace(3, 10000000, 10)
    print(r2)
    
if __name__ == "__main__":
    test4()

随机张量

使用torch.randn 创建随机张量。 使用随机数种子。

随机数种子

import torch

def test1():
    # 设置随机数种子
    torch.manual_seed(123)

    # 获取随机数种子
    print(torch.initial_seed())

if __name__ == "__main__":
    test1()

随机张量

在 PyTorch 中，种子影响所有与随机性相关的操作，包括张量的随机初始化、数据的随机打乱、模型的参数初始化等。通过设置随机数种子，可以做到模型训练和实验结果在不同的运行中进行复现。

import torch

def test001():
    # 1.设置随机数种子
    torch.manual_seed(123)

    # 2.获取随机数种子，需要查看种子时调用
    print(torch.initial_seed())

    # 3.生成随机张量，均匀分布（范围 [0, 1)）
    # 创建2个样本，每个样本3个特征
    print(torch.rand(2, 3))

    # 4.生成随机张量：标准正态分布（均值 0，标准差 1）
    print(torch.randn(2, 3))

    # 5.原生服从正态分布：均值为2， 方差为3，形状为1*4的正态分布
    print(torch.normal(mean=2, std=3, size=(1, 4)))

if __name__ == "__main__":
    test001()

三、Tensor常见属性

获取属性

import torch
def test1():
    data = torch.tensor([1, 2, 3])
    # 张量的数据类型、所在设备、形状
    print(data.dtype, data.device, data.shape)

if __name__ == "__main__":
    test1()

切换设备

import torch
def test001():
    data = torch.tensor([1, 2, 3])
    print(data.dtype, data.device, data.shape)

    # 把数据切换到GPU进行运算
    device = "cuda" if torch.cuda.is_available() else "cpu"
    data = data.to(device)
    print(data.device)

if __name__ == "__main__":
    test001()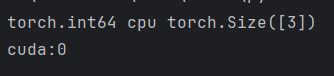

类型转换

import torch
def test001():
    data = torch.tensor([1, 2, 3])
    print(data.dtype)  # torch.int64

    # 1. 使用type进行类型转换
    data = data.type(torch.float32)
    print(data.dtype)  # float32
    data = data.type(torch.float16)
    print(data.dtype)  # float16

    # 2. 使用类型方法
    data = data.float()
    print(data.dtype)  # float32
    # 16 位浮点数，torch.float16，即半精度
    data = data.half()
    print(data.dtype)  # float16
    data = data.double()
    print(data.dtype)  # float64
    data = data.long()
    print(data.dtype)  # int64
    data = data.int()
    print(data.dtype)  # int32

    #  使用dtype属性
    data = torch.tensor([1, 2, 3], dtype=torch.half)
    print(data.dtype)

if __name__ == "__main__":
    test001()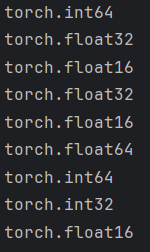

四、Tensor数据转换

共享内存问题：PyTorch与NumPy的转换默认共享内存，修改会影响原始数据

Tensor与Numpy

张量转numpy

def test1():
    # 张量转numpy   浅拷贝
    t_tensor= torch.tensor([1,2,5])
    t_numpy= t_tensor.numpy()
    t_numpy[0]=2
    #深拷贝
    t_numpy1=t_tensor.numpy().copy()
    print(t_tensor)
    print(t_numpy)
    print(t_numpy1)

if __name__=='__main__':
    test1()

numpy转张量

def test3():
    #numpy转张量   浅拷贝
    t_numpy=np.array([1,2,3])
    t_tensor=torch.from_numpy(t_numpy)
    print(t_numpy)
    print(t_tensor)

    #深拷贝
    t_numpy=np.array([[1,3,2],[4,6,2]])
    t_tensor=torch.tensor(t_numpy)
    print(t_numpy)
    print(t_tensor)

if __name__=='__main__':
    test3()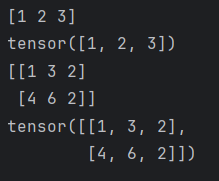

五、Tensor常见操作

获取元素值

def test1():
    t = torch.tensor(10)
    print(t.item())

    t2=torch.tensor([[10]])
    print(t2.item())

if __name__=='__main__':
    test1()

阿达玛积

import torch
# 点积：对应位置相乘但是不相加
def test1():
    data1 = torch.tensor([[1, 2, 3], [4, 5, 6]])
    data2 = torch.tensor([[2, 3, 4], [2, 2, 3]])
    print(data1 * data2)

def test2():
    data1 = torch.tensor([[1, 2, 3], [4, 5, 6]])
    data2 = torch.tensor([[2, 3, 4], [2, 2, 3]])
    print(data1.mul(data2))

if __name__ == "__main__":
    test1()
    test2()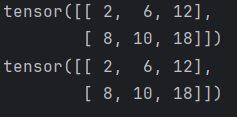

Tensor相乘

import torch
def test6():
    data1 = torch.tensor([
        [1, 2, 3],
        [4, 5, 6]
    ])
    data2 = torch.tensor([
        [3, 2],
        [2, 3],
        [5, 3]
    ])
    print(data1 @ data2)
    print(data1.matmul(data2))

if __name__ == "__main__":
    test6()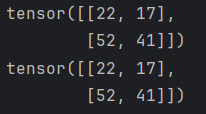

形状操作

reshape

import torch
def test001():
    #0-10随机生成4行3列数据
    data = torch.randint(0, 10, (4, 3))
    print(data)
    # 1. 使用reshape改变形状
    # 包含 2 个块，每个块包含 2 行，每行包含 3 个元素
    data = data.reshape(2, 2, 3)
    print(data)

    # 2. 使用-1表示自动计算
    data = data.reshape(2, -1)
    print(data)

if __name__ == "__main__":
    test001()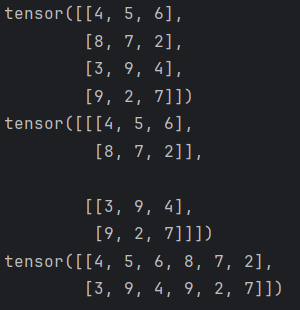

view

view进行形状变换的特征：

• 张量在内存中是连续的；

• 返回的是原始张量视图，不重新分配内存，效率更高;

• 如果张量在内存中不连续，view 将无法执行，并抛出错误。

与reshape比较：

view：高效，但需要张量在内存中是连续的；

reshape：更灵活，但涉及内存复制；

内存连续性

张量的内存布局决定了其元素在内存中的存储顺序。对于多维张量，内存布局通常按照最后一个维度优先 的顺序存储，即先存列，后存行。例如，对于一个二维张量 A，其形状为 (m, n)，其内存布局是先存储第 0 行的所有列元素，然后是第 1 行的所有列元素，依此类推。

如果张量的内存布局与形状完全匹配，并且没有被某些操作（如转置、索引等）打乱，那么这个张量就是连续的。

PyTorch 的大多数操作都是基于 C 顺序的，我们在进行变形或转置操作时，很容易造成内存的不连续性。

import torch
def test1():
    tensor = torch.tensor([[1, 2, 3], [4, 5, 6]])
    print("正常情况下的张量：", tensor.is_contiguous())

    # 对张量进行转置操作
    tensor = tensor.t()
    print("转置操作的张量：", tensor.is_contiguous())
    print(tensor)
    # 此时使用view进行变形操作
    # view要求张量连续
    tensor = tensor.view(2, -1)
    print(tensor)

if __name__ == "__main__":
    test1()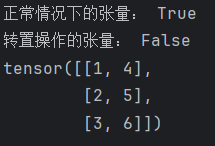

view变形操作

import torch
def test2():
    tensor = torch.tensor([[1, 2, 3], [4, 5, 6]])
    # 将 2x3 的张量转换为 3x2
    reshaped_tensor = tensor.view(3, 2)
    print(reshaped_tensor)

    # 自动推断一个维度，每个维度两个数据
    reshaped_tensor = tensor.view(-1, 2)
    print(reshaped_tensor)

if __name__ == "__main__":
    test2()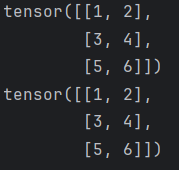

transpose

transpose 用于交换张量的两个维度，注意，是2个维度，它返回的是原张量的视图。

import torch
def test3():
    data = torch.randint(0, 10, (3, 4, 5))
    print(data, data.shape)

    # 使用transpose进行形状变换，原始数据的0维度和1维度
    transpose_data = torch.transpose(data,0,1)

    # transpose_data = data.transpose(0, 1)
    print(transpose_data, transpose_data.shape)

if __name__ == "__main__":
    test3()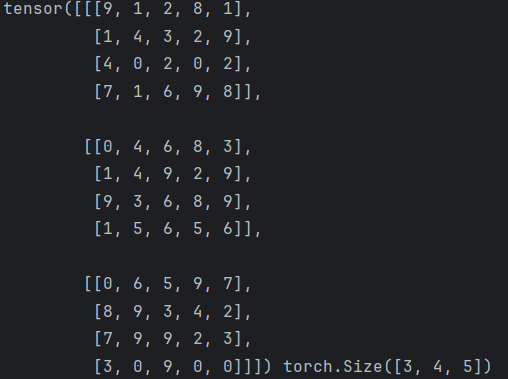

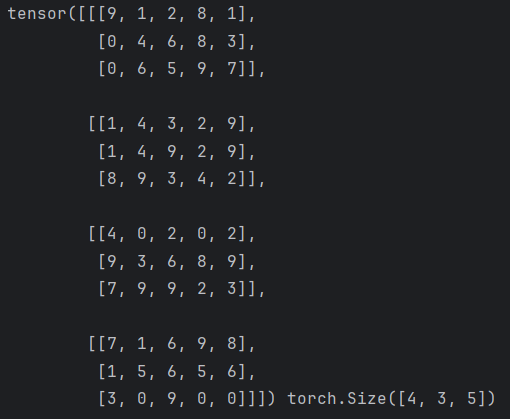
permute

通过重新排列张量的维度来返回一个新的张量，不改变张量的数据，只改变维度的顺序。

import torch
def test4():
    data = torch.randint(0, 10, (3, 4, 5))
    print(data, data.shape)
    # 使用permute进行多维度形状变换
    permute_data = data.permute(1, 2, 0)
    print(permute_data, permute_data.shape)

if __name__ == "__main__":
    test4()

和 transpose 一样，permute 返回新张量，原张量不变。

变维

unsqueeze：用于在指定位置插入一个大小为 1 的新维度。

squeeze：用于移除所有大小为 1 的维度，或者移除指定维度的大小为 1 的维度。

降维

import torch

def test006():
    data = torch.randint(0, 10, (1, 4, 5, 1))
    print(data, data.shape)

    # 进行降维操作
    data1 = data.squeeze(0).squeeze(-1)
    print(data.shape)
    
    # 移除所有大小为 1 的维度
	data2 = torch.squeeze(data)
    
    # 尝试移除第 1 维（大小为 3，不为 1，不会报错，张量保持不变。）
	data3 = torch.squeeze(data, dim=1)
	print("尝试移除第 1 维后的形状:", data3.shape)

if __name__ == "__main__":
    test006()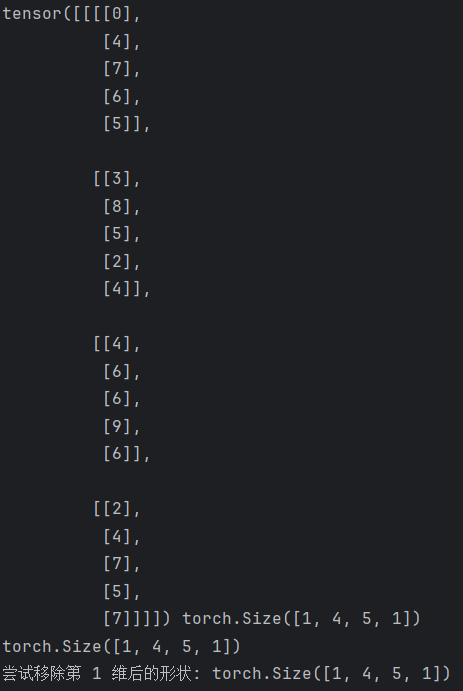

升维

import torch
def test7():
    data = torch.randint(0, 10, (32, 32, 3))
    print(data.shape)
    # 升维操作
    data = data.unsqueeze(0)
    print(data.shape)

if __name__ == "__main__":
    test7()

广播机制

广播机制允许在对不同形状的张量进行计算，而无需显式地调整它们的形状。广播机制通过自动扩展较小维度的张量，使其与较大维度的张量兼容，从而实现按元素计算。

广播机制需要遵循以下规则：

• 每个张量的维度至少为1

• 满足右对齐

import torch
def test6():
    data1d = torch.tensor([1, 2, 3])
    data2d = torch.tensor([[4], [2], [3]])
    print(data1d.shape, data2d.shape)
    # 进行计算：会自动进行广播机制
    print(data1d + data2d)

if __name__ == "__main__":
    test6()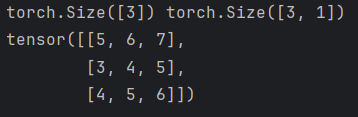

六、自动微分

自动微分模块torch.autograd负责自动计算张量操作的梯度，具有自动求导功能。自动微分模块是构成神经网络训练的必要模块，可以实现网络权重参数的更新，使得反向传播算法的实现变得简单而高效。

计算梯度

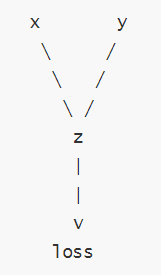
在上述代码中，x 和 y 是输入张量，即叶子节点，z 是中间结果，loss 是最终输出。每一步操作都会记录依赖关系：

z = x * y：z 依赖于 x 和 y。

loss = z.sum()：loss 依赖于 z。

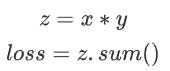
叶子节点：

在 PyTorch 的自动微分机制中，叶子节点（leaf node） 是计算图中：

• 由用户直接创建的张量，并且它的 requires_grad=True。

• 这些张量是计算图的起始点，通常作为模型参数或输入变量。

特征：

• 没有由其他张量通过操作生成。

• 如果参与了计算，其梯度会存储在 leaf_tensor.grad 中。

• 默认情况下，叶子节点的梯度不会自动清零，需要显式调用 optimizer.zero_grad() 或 x.grad.zero_() 清除。

判断叶子节点

x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)  # 叶子节点
y = x ** 2  # 非叶子节点（通过计算生成）
z = y.sum()

print(x.is_leaf)  # True
print(y.is_leaf)  # False
print(z.is_leaf)  # False

叶子节点与非叶子节点的区别

特性	叶子节点	非叶子节点
创建方式	用户直接创建的张量	通过其他张量的运算生成
is_leaf 属性	True	False
梯度存储	梯度存储在 .grad 属性中	梯度不会存储在 .grad，只能通过反向传播传递
是否参与计算图	是计算图的起点	是计算图的中间或终点
删除条件	默认不会被删除	在反向传播后，默认被释放（除非 retain_graph=True）

特点：

• 返回的张量是一个新的张量，与原始张量共享数据。

• 对 x.detach() 的操作不会影响原始张量的梯度计算。

• 推荐使用 detach()，因为它更安全，且在未来版本的 PyTorch 中可能会取代 data。

反向传播

使用tensor.backward()方法执行反向传播，从而计算张量的梯度。这个过程会自动计算每个张量对损失函数的梯度。例如：调用 loss.backward() 从输出节点 loss 开始，沿着计算图反向传播，计算每个节点的梯度。

梯度

计算得到的梯度通过tensor.grad访问，这些梯度用于优化模型参数，以最小化损失函数。

标量梯度计算

import torch
def test001():
    x = torch.tensor(10.5, requires_grad=True)
    print(x.requires_grad)  # True

    # 1. 默认y的requires_grad=True
    y = x**2 + 2 * x + 3
    print(y.requires_grad)  # True

    # 2. 如果不需要y计算梯度-with进行上下文管理
    with torch.no_grad():
        y = x**2 + 2 * x + 3
    print(y.requires_grad)  # False

    # 3. 如果不需要y计算梯度-使用装饰器
    @torch.no_grad()
    def y_fn(x):
        return x**2 + 2 * x + 3

    y = y_fn(x)
    print(y.requires_grad)  # False

    # 4. 如果不需要y计算梯度-全局设置，需要谨慎
    torch.set_grad_enabled(False)
    y = x**2 + 2 * x + 3
    print(y.requires_grad)  # False

if __name__ == "__main__":
    test001()

向量梯度计算

import torch
def test3():
    # 1. 创建张量：必须为浮点类型
    x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
    # 2. 操作张量
    y = x ** 2
    # 3. 计算梯度，也就是反向传播
    y.backward()
    # 4. 读取梯度值
    print(x.grad)

if __name__ == "__main__":
    test3()

以上会报错：错误预警：RuntimeError: grad can be implicitly created only for scalar outputs

import torch
def test002():
    # 1. 创建张量：必须为浮点类型
    x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)

    # 2. 操作张量
    y = x ** 2

    # 3. 损失函数
    loss = y.mean()

    # 4. 计算梯度，也就是反向传播
    loss.backward()

    # 5. 读取梯度值
    print(x.grad)

if __name__ == "__main__":
    test002()

多标量梯度计算

由于 y 是一个向量，我们需要提供一个与 y 形状相同的向量作为 backward() 的参数，这个参数通常被称为 梯度张量 （gradient tensor），它表示 y 中每个元素的梯度。

import torch
def test3():
    # 1. 创建两个标量
    x1 = torch.tensor(5.0, requires_grad=True, dtype=torch.float64)
    x2 = torch.tensor(3.0, requires_grad=True, dtype=torch.float64)

    # 2. 构建运算公式
    y = x1 ** 2 + 2 * x2 + 7

    # 3. 计算梯度，也就是反向传播
    y.backward()

    # 4. 读取梯度值
    print(x1.grad, x2.grad)

    # 输出：
    # tensor(10., dtype=torch.float64) tensor(2., dtype=torch.float64)
if __name__ == "__main__":
    test3()

多向量梯度计算

import torch
def test4():
    # 创建两个张量，并设置 requires_grad=True
    x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
    y = torch.tensor([4.0, 5.0, 6.0], requires_grad=True)

    # 前向传播：计算 z = x * y
    z = x * y

    # 前向传播：计算 loss = z.sum()
    loss = z.sum()

    # 查看前向传播的结果
    print("z:", z)  # 输出: tensor([ 4., 10., 18.], grad_fn=<MulBackward0>)
    print("loss:", loss)  # 输出: tensor(32., grad_fn=<SumBackward0>)

    # 反向传播：计算梯度
    loss.backward()

    # 查看梯度
    print("x.grad:", x.grad)  # 输出: tensor([4., 5., 6.])
    print("y.grad:", y.grad)  # 输出: tensor([1., 2., 3.])

if __name__ == "__main__":
    test4()

梯度上下文控制

梯度计算的上下文控制和设置对于管理计算图、内存消耗、以及计算效率至关重要。

控制梯度计算

import torch
def test1():
    x = torch.tensor(10.5, requires_grad=True)
    print(x.requires_grad)  # True

    # 1. 默认y的requires_grad=True
    y = x**2 + 2 * x + 3
    print(y.requires_grad)  # True

    # 2. 如果不需要y计算梯度-with进行上下文管理
    with torch.no_grad():
        y = x**2 + 2 * x + 3
    print(y.requires_grad)  # False

    # 3. 如果不需要y计算梯度-使用装饰器
    @torch.no_grad()
    def y_fn(x):
        return x**2 + 2 * x + 3

    y = y_fn(x)
    print(y.requires_grad)  # False

    # 4. 如果不需要y计算梯度-全局设置，需要谨慎
    torch.set_grad_enabled(False)
    y = x**2 + 2 * x + 3
    print(y.requires_grad)  # False

if __name__ == "__main__":
    test1()

累计梯度

默认情况下，当我们重复对一个自变量进行梯度计算时，梯度是累加的

import torch
def test2():
    # 1. 创建张量：必须为浮点类型
    x = torch.tensor([1.0, 2.0, 5.3], requires_grad=True)

    # 2. 累计梯度：每次计算都会累计梯度
    for i in range(3):
        y = x**2 + 2 * x + 7
        z = y.mean()
        z.backward()
        print(x.grad)

if __name__ == "__main__":
    test2()

梯度清零

import torch
def test2():
    # 1. 创建张量：必须为浮点类型
    x = torch.tensor([1.0, 2.0, 5.3], requires_grad=True)

    # 2. 累计梯度：每次计算都会累计梯度
    for i in range(3):
        y = x**2 + 2 * x + 7
        z = y.mean()
        # 2.1 反向传播之前先对梯度进行清零
        if x.grad is not None:
            x.grad.zero_()
            
        z.backward()
        print(x.grad)

if __name__ == "__main__":
    test2()
    
# 输出：
# tensor([1.3333, 2.0000, 4.2000])
# tensor([1.3333, 2.0000, 4.2000])
# tensor([1.3333, 2.0000, 4.2000])

总结

以上便是此次对于张量的部分总结操作，如若文章有错或是您还有疑问，欢迎在评论区指正提出，我会尽快的帮助解决，感谢您的阅读！