专题一 向量的基本运算
注意:行列式、逆、伴随矩阵都是方阵
1.向量的定义
称为
维行向量,
为
维列向量。
相当于n维向量的n维坐标,从0点出发。
2.向量加法的定义
向量加法的定义 设,
,称
为
与
的和,记作
。
3.向量数乘的定义
向量数乘的定义 设,
为常数,称
为
与
的数乘,记作
。
4.向量内积的定义
向量内积的定义 设,
,称
为
与
的内积 ,记作
。 若
,则称
与
正交。
内积即为一行乘一列。
显然零向量与任意向量均正交。
类比两直线垂直:
垂直条件:
垂直条件的推导过程:
两点:
5.向量长度的定义
设,称
为的长度(模),记作
。
若,则称
为单位向量。点在单位圆上
6.正交矩阵的定义
设为
阶矩阵,若
或
,则称
为正交矩阵 。
叫做内积
7.正交矩阵的充要条件
为
阶正交矩阵
的列(或行)向量组为单位正交的向量组
证明:
由,得
从而
故单位正交
8.正交矩阵的性质
正交矩阵的性质
(1);
证明:,由
(2)若为
阶正交矩阵,则
均为正交矩阵.
证明:
9.Schmidt正交化的定义
Schmidt 正交化的定义 设向量组 线性无关,令
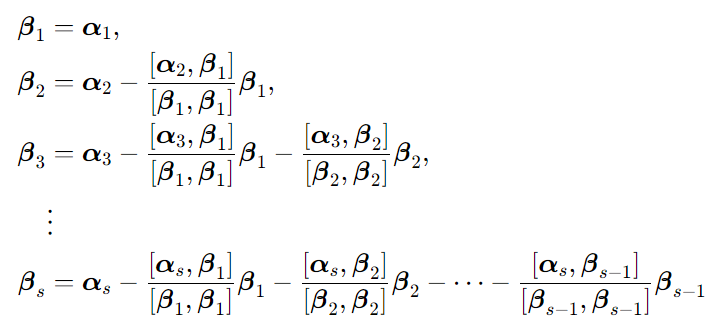 则
则 两两正交,将其单位化,除以他的模,得
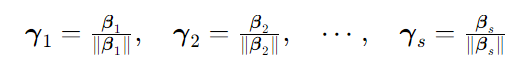
则为单位正交的向量组,
从 到
的过程称为Schmidt 正交化.
专题二 线性表示
1.线性组合的定义
设向量组 ,对任意一组数
,称
为
的线性组合。
2.线性表示的定义
设向量组 与向量
,若存在一组数
,使得
,则称
可由
线性表示。
示例 设,
,
,
,则
。
3.向量组等价的定义
设向量组(I),向量组(II)
,若向量组(II)中的每个向量 均可由向量组(I)线性表示,则称向量组(II)可由向量组(I)线性表示。
若向量组(I)与(II)可以相互线性表示 ,则称向量组(I)与(II)等价。
示例 设
向量组(I),
向量组(II),
则
,
故向量组(I)与(II)等价。
4.线性表示的充要条件
非零向量 可由向量组
线性表示
非齐次线性方程组
有解
系数矩阵和增广矩阵
5.向量组等价的充要条件
向量组(I) 与向量组(II)
等价
三秩相等,向量组等价
6.线性表示的充分条件
设向量组线性无关,向量组
线性相关,则
可由
唯一地线性表示。
7.☆线性表示的求法
设向量 可由向量组
线性表示,对
作初等行变换 ,化为行最简形 矩阵,解得线性表示的系数。
行最简形:每行第一个非零的数为1,1的下方和上方均为0(单位矩阵是行最简形)
专题三 线性相关与线性无关
1.线性相关与线性无关的定义
设向量组,若存在不全为零 的数
,使得
则称
线性相关,否则称其线性无关.
线性无关的定义:若线性组合为0,则系数全为0
【评注】
(1)向量 线性相关
;一个向量相关。
向量组 线性相关
对应分量成比例;两个向量相关。
(2)两个向量 线性相关的几何意义 是两个向量共线;
三个向量 线性相关的几何意义是三个向量共面.
2.线性相关的充要条件
向量组线性相关
至少有一个向量可由其余向量线性表示
证明:
齐次线性方程组
有非零解
非零解:能线性表示,不全为0,有非零解
推论 个
维向量
线性相关
3.线性相关的充分条件
(1)含有零向量的向量组线性相关;
证明:
(2)部分相关,则整体相关;
(3)高维相关,则低维相关;
例如:,4维相关,2维相关,
(4)设向量组 可由向量组
线性表示,且
,则
线性相关(即以少表多,则多必相关);
逆否命题:设向量组 线性无关,可由向量组
线性表示,则
(即无关被表,则个数不多)。(无关向量组)(小于)
推论 个
维向量(即向量维数小于向量个数)线性相关。
例如:任意4个3维向量均可由表示(以少表多)
4.线性无关的充要条件
向量组线性无关
任意向量均不能由其余向量线性表示
齐次线性方程组
只有零解
推论 个
维向量
线性无关
5.线性无关的充分条件
(1)整体无关,则部分无关;
(2)低维无关,则高维无关;
(3)不含零向量的正交向量组线性无关;
证明:
(4)不同特征值的特征向量线性无关。
专题四 极大线性无关组与向量组的秩
1.极大线性无关组的定义
设向量组中存在
个向量
线性无关,再加入其余任意向量 就线性相关 (其余向量均可由其线性表示),则称
为
的极大线性无关组。
2.向量组的秩的定义
极大线性无关组中向量的个数 称为向量组的秩。
【评注】 (1)极大线性无关组不唯一 ,若向量组的秩为 ,则任意
个线性无关的向量 均为极大线性无关组;
例如:
均为极大无关组,r=2。2个
(2)矩阵的秩 等于其列向量组的秩 ,也等于其行向量组的秩。
例如:的秩为2
3.极大线性无关组的求法
对 作初等行变换 ,化为行阶梯形矩阵 ,则行阶梯形矩阵中每行第一个非零元素 对应的列向量 构成极大线性无关组
例如:
为极大无关组