前言
随机向量正交投影定理(Orthogonal Projection Theorem, OPT) 是理解和推导卡尔曼了滤波(Kalman Filtrering, KF) 重要理论工具,简化卡尔曼最优滤波方程推导过程并提供数学严密性。本文介绍该定理内容及证明过程,并给出该定理的4个推论,其中推论4是最重要的更新信息定理,并给出其证明过程。
随机向量正交定义
设XXX为nnn维随机向量,ZZZ为mmm维随机向量,如果存在:
E[XZT]=0 \begin{align*} E[XZ^{T}]=\mathbf{0} \tag{1} \end{align*} E[XZT]=0(1)
则称XXX与ZZZ正交。
注意:
X=[x1x2⋮xn],Z=[z1z2⋮zm] \begin{align*} X=\begin{bmatrix} x_{1} \\ x_{2} \\ \vdots\\ x_{n} \\ \end{bmatrix} , Z = \begin{bmatrix} z_{1} \\ z_{2} \\ \vdots \\ z_{m} \\ \end{bmatrix} \tag{2} \end{align*} X= x1x2⋮xn ,Z= z1z2⋮zm (2)
XZT=[x1x2⋮xn][z1z2⋯zm]=[x1z1x1z2⋯x1zmx2z1x2z2⋯x2zm⋮⋮⋮⋮xnz1xnz2⋯xnzm] \begin{align*} XZ^{T}=\begin{bmatrix} x_{1} \\ x_{2} \\ \vdots\\ x_{n} \\ \end{bmatrix} \begin{bmatrix} z_{1} z_{2} \cdots z_{m} \\ \end{bmatrix} = \begin{bmatrix} x_{1}z_{1} &x_{1}z_{2} &\cdots &x_{1}z_{m} \\ x_{2}z_{1} &x_{2}z_{2} &\cdots &x_{2}z_{m} \\ \vdots &\vdots &\vdots &\vdots \\ x_{n}z_{1} &x_{n}z_{2} &\cdots &x_{n}z_{m} \\ \end{bmatrix}\tag{3} \end{align*} XZT= x1x2⋮xn [z1z2⋯zm]= x1z1x2z1⋮xnz1x1z2x2z2⋮xnz2⋯⋯⋮⋯x1zmx2zm⋮xnzm (3)
式(1)等价于:
E[XZT]=E[[x1z1x1z2⋯x1zmx2z1x2z2⋯x2zm⋮⋮⋮⋮xnz1xnz2⋯xnzm]]=[00⋯000⋯0⋮⋮⋮⋮00⋯0]=0 \begin{align*} E[XZ^{T}]= E \left [ \begin{bmatrix} x_{1}z_{1} &x_{1}z_{2} &\cdots &x_{1}z_{m} \\ x_{2}z_{1} &x_{2}z_{2} &\cdots &x_{2}z_{m} \\ \vdots &\vdots &\vdots &\vdots \\ x_{n}z_{1} &x_{n}z_{2} &\cdots &x_{n}z_{m} \\ \end{bmatrix} \right ] = \begin{bmatrix} 0 &0 &\cdots &0 \\ 0 &0 &\cdots &0 \\ \vdots &\vdots &\vdots &\vdots \\ 0 &0 &\cdots &0 \\ \end{bmatrix} = \mathbf{0}\tag{4} \end{align*} E[XZT]=E x1z1x2z1⋮xnz1x1z2x2z2⋮xnz2⋯⋯⋮⋯x1zmx2zm⋮xnzm = 00⋮000⋮0⋯⋯⋮⋯00⋮0 =0(4)
这里给出正交、独立和不相关的关系结论[2]:
- 独立一定不相关,但不相关不一定独立。特殊情况:当都服从正态分布时不相关等价于独立。
- 如果其中至少一个随机向量的数学期望为零,则不相关与正交等价。
- 如果都服从正态分布,且至少有一个数学期望为零,则正交、独立和不相关三者等价。
随机向量正交投影定义
设XXX为nnn维随机向量,ZZZ为mmm维随机向量,如果存在某个n×mn \times mn×m阶矩阵A∗A^{*}A∗和某个nnn维常数向量b∗b^{*}b∗,对任意n×mn \times mn×m阶矩阵AAA和任意的nnn维向量bbb能使下式恒成立:
E[(X−(A∗Z+b∗))(AZ+b)T]=0 \begin{align*} E[(X-(A^{*}Z+b^{*}))(AZ+b)^{T}] = \mathbf{0} \tag{5} \\ \end{align*} E[(X−(A∗Z+b∗))(AZ+b)T]=0(5)
则称A∗Z+b∗A^{*}Z+b^{*}A∗Z+b∗为XXX在ZZZ上的正交投影。
将式(5)改写为:
E[(X−(A∗Z+b∗))(AZ+b)T]=E[((X−(A∗Z+b∗))ZT]AT+E[X−(A∗Z+b∗)]bT=0 \begin{align*} E[(X-(A^{*}Z+b^{*}))(AZ+b)^{T}] = E[((X-(A^{*}Z+b^{*}))Z^{T}]A^{T} + E[X-(A^{*}Z+b^{*})]b^{T}=\mathbf{0} \tag{6} \\ \end{align*} E[(X−(A∗Z+b∗))(AZ+b)T]=E[((X−(A∗Z+b∗))ZT]AT+E[X−(A∗Z+b∗)]bT=0(6)
由于A为任意n×mn \times mn×m阶矩阵,b为nnn维任意向量,要使上式恒成立,须有:
E[(X−(A∗Z+b∗))ZT]=0E[X−(A∗Z+b∗)]=0} \begin{align*} \left.\begin{matrix} E[(X-(A^{*}Z+b^{*}))Z^{T}] = \mathbf{0} & \\ E[X-(A^{*}Z+b^{*})] = \mathbf{0} & \end{matrix}\right\} \tag{7} \end{align*} E[(X−(A∗Z+b∗))ZT]=0E[X−(A∗Z+b∗)]=0}(7)
式(7)是正交投影的另一种形式。
如果XXX作为被估向量,ZZZ作为观测向量,对于定义的理解:
- 正交投影A∗Z+b∗A^{*}Z+b^{*}A∗Z+b∗为观测向量ZZZ和常数向量bbb的线性组合;
- 由任意n×mn \times mn×m阶矩阵AAA和任意nnn维向量bbb及观测向量ZZZ的所有线性组合AZ+bAZ+bAZ+b构成ZZZ张成的量测空间;
- 对应式 (5),若用正交投影A∗Z+b∗A^{*}Z+b^{*}A∗Z+b∗作为XXX的估计,则估计误差与量测空间AZ+bAZ+bAZ+b正交;
- 对应式 (7),若用正交投影A∗Z+b∗A^{*}Z+b^{*}A∗Z+b∗作为XXX的估计,则估计误差与观测向量ZZZ正交,实际上观测向量ZZZ本身也位于量测空间AZ+bAZ+bAZ+b上;
- 对应式 (7),若用正交投影A∗Z+b∗A^{*}Z+b^{*}A∗Z+b∗作为XXX的估计,则其为无偏估计。
随机向量正交投影定理
设XXX和ZZZ具有二阶矩,则XXX在ZZZ上的正交投影A∗Z+b∗A^{*}Z+b^{*}A∗Z+b∗即为XXX在ZZZ上的线性最小方差估计E∗[X∣Z]E^{*}[X|Z]E∗[X∣Z],反之亦然,即:
A∗Z+b∗=E∗[X∣Z] \begin{align*} A^{*}Z+b^{*}=E^{*}[X|Z] \tag{8} \end{align*} A∗Z+b∗=E∗[X∣Z](8)
充分性证明:
若正交投影A∗Z+b∗A^{*}Z+b^{*}A∗Z+b∗作为XXX在ZZZ上的估计,由式(7)的估计误差的无偏性,得
E[X−(A∗Z+b∗)]=E[X]−A∗E[Z]−b∗=0b∗=E[X]−A∗E[Z]A∗Z+b∗=A∗Z+E[X]−A∗E[Z]=E[X]+A∗(Z−E[Z])X−(A∗Z+b∗)=X−E[X]−A∗(Z−E[Z]) \begin{align*} E[X-(A^{*}Z+b^{*})] &= E[X]-A^{*}E[Z]-b^{*} = \mathbf{0} \tag{9} \\ b^{*} &= E[X]-A^{*}E[Z] \tag{10} \\ A^{*}Z+b^{*} &= A^{*}Z+E[X]-A^{*}E[Z]=E[X]+A^{*}(Z-E[Z]) \tag{11} \\ X-(A^{*}Z+b^{*}) &= X-E[X]-A^{*}(Z-E[Z]) \tag{12} \end{align*} E[X−(A∗Z+b∗)]b∗A∗Z+b∗X−(A∗Z+b∗)=E[X]−A∗E[Z]−b∗=0=E[X]−A∗E[Z]=A∗Z+E[X]−A∗E[Z]=E[X]+A∗(Z−E[Z])=X−E[X]−A∗(Z−E[Z])(9)(10)(11)(12)
由式(7)的估计误差与观测向量ZZZ正交,得
E[(X−(A∗Z+b∗))ZT]=0E[(X−E[X]−A∗(Z−E[Z]))ZT]=0E[(X−E[X]−A∗(Z−E[Z]))((Z−E[Z])+E[Z])T]=0E[(X−E[X]−A∗(Z−E[Z]))((Z−E[Z])+E[Z])T]=0E[(X−E[X]−A∗(Z−E[Z]))(Z−E[Z])T]+E[(X−E[X]−A∗(Z−E[Z]))E[Z]T]=0E[(X−E[X])(Z−E[Z])T−A∗(Z−E[Z])(Z−E[Z])T]=0E[(X−E[X])(Z−E[Z])T]−A∗E[(Z−E[Z])(Z−E[Z])T]=0Cov(X,Z)−A∗Var(Z)=0A∗=Cov(X,Z)Var(Z)−1 \begin{align*} E[(X-(A^{*}Z+b^{*}))Z^{T}] &= \mathbf{0} \\ E[(X-E[X]-A^{*}(Z-E[Z]))Z^{T}] &= \mathbf{0} \\ E[(X-E[X]-A^{*}(Z-E[Z]))((Z-E[Z])+E[Z])^{T}] &= \mathbf{0} \\ E[(X-E[X]-A^{*}(Z-E[Z]))((Z-E[Z])+E[Z])^{T}] &= \mathbf{0} \\ E[(X-E[X]-A^{*}(Z-E[Z]))(Z-E[Z])^{T}]+E[(X-E[X]-A^{*}(Z-E[Z]))E[Z]^{T}] &= \mathbf{0} \\ E[(X-E[X])(Z-E[Z])^{T}-A^{*}(Z-E[Z])(Z-E[Z])^{T}] &= \mathbf{0} \\ E[(X-E[X])(Z-E[Z])^{T}]-A^{*}E[(Z-E[Z])(Z-E[Z])^{T}] &= \mathbf{0} \\ Cov(X,Z)-A^{*}Var(Z) &= \mathbf{0} \\ A^{*}&= Cov(X,Z)Var(Z)^{-1} \tag{13} \\ \end{align*} E[(X−(A∗Z+b∗))ZT]E[(X−E[X]−A∗(Z−E[Z]))ZT]E[(X−E[X]−A∗(Z−E[Z]))((Z−E[Z])+E[Z])T]E[(X−E[X]−A∗(Z−E[Z]))((Z−E[Z])+E[Z])T]E[(X−E[X]−A∗(Z−E[Z]))(Z−E[Z])T]+E[(X−E[X]−A∗(Z−E[Z]))E[Z]T]E[(X−E[X])(Z−E[Z])T−A∗(Z−E[Z])(Z−E[Z])T]E[(X−E[X])(Z−E[Z])T]−A∗E[(Z−E[Z])(Z−E[Z])T]Cov(X,Z)−A∗Var(Z)A∗=0=0=0=0=0=0=0=0=Cov(X,Z)Var(Z)−1(13)
将式(13)带入式(10),得
b∗=E[X]−A∗E[Z]=E[X]−Cov(X,Z)Var(Z)−1E[Z] \begin{align*} b^{*} &= E[X]-A^{*}E[Z] \\ &= E[X]-Cov(X,Z)Var(Z)^{-1}E[Z] \tag{14} \\ \end{align*} b∗=E[X]−A∗E[Z]=E[X]−Cov(X,Z)Var(Z)−1E[Z](14)
由式(13)和(14),正交投影即为:
A∗Z+b∗=Cov(X,Z)Var(Z)−1Z+E[X]−Cov(X,Z)Var(Z)−1E[Z]=E[X]+Cov(X,Z)Var(Z)−1(Z−E[Z]) \begin{align*} A^{*}Z+b^{*} &= Cov(X,Z)Var(Z)^{-1}Z + E[X]-Cov(X,Z)Var(Z)^{-1}E[Z]\\ &= E[X]+Cov(X,Z)Var(Z)^{-1}(Z-E[Z]) \tag{15} \\ \end{align*} A∗Z+b∗=Cov(X,Z)Var(Z)−1Z+E[X]−Cov(X,Z)Var(Z)−1E[Z]=E[X]+Cov(X,Z)Var(Z)−1(Z−E[Z])(15)
又由线性最小方差估计为:
E∗[X∣Z]=E[X]+Cov(X,Z)Var(Z)−1(Z−E[Z]) \begin{align*} E^{*}[X|Z] &= E[X]+Cov(X,Z)Var(Z)^{-1}(Z-E[Z]) \tag{16} \\ \end{align*} E∗[X∣Z]=E[X]+Cov(X,Z)Var(Z)−1(Z−E[Z])(16)
故证明式(8)成立,即
A∗Z+b∗=E∗[X∣Z] \begin{align*} A^{*}Z+b^{*}&= E^{*}[X|Z] \\ \end{align*} A∗Z+b∗=E∗[X∣Z]
充分性证毕。
必要性证明:
由线性最小方差估计的无偏性,可直接得,
E[X−E∗[X∣Z]]=E[X−E[X]−Cov(X,Z)Var(Z)−1(Z−E[Z])]=E[X−E[X]]−Cov(X,Z)Var(Z)−1E[Z−E[Z]]=0 \begin{align*} E[X-E^{*}[X|Z]] &= E[X-E[X]-Cov(X,Z)Var(Z)^{-1}(Z-E[Z])] \\ &= E[X-E[X]]-Cov(X,Z)Var(Z)^{-1}E[Z-E[Z]] \\ &=\mathbf{0} \tag{17} \\ \end{align*} E[X−E∗[X∣Z]]=E[X−E[X]−Cov(X,Z)Var(Z)−1(Z−E[Z])]=E[X−E[X]]−Cov(X,Z)Var(Z)−1E[Z−E[Z]]=0(17)
又
E[(X−E∗[X∣Z])ZT]=E[(X−E[X]−Cov(X,Z)Var(Z)−1(Z−E[Z]))ZT]=E[(X−E[X])ZT]−Cov(X,Z)Var(Z)−1E[(Z−E[Z])ZT]=E[XZT]−E[X]E[Z]T−Cov(X,Z)Var(Z)−1E[ZZT]+Cov(X,Z)Var(Z)−1E[Z]E[Z]T \begin{align*} E[(X-E^{*}[X|Z])Z^{T}] &= E[(X-E[X]-Cov(X,Z)Var(Z)^{-1}(Z-E[Z]))Z^{T} ] \\ &= E[(X-E[X])Z^{T}] - Cov(X,Z)Var(Z)^{-1} E[(Z-E[Z])Z^{T}] \\ &= E[XZ^{T}] -E[X]E[Z]^{T}-Cov(X,Z)Var(Z)^{-1} E[ZZ^{T}]+Cov(X,Z)Var(Z)^{-1}E[Z]E[Z]^{T} \tag{18} \end{align*} E[(X−E∗[X∣Z])ZT]=E[(X−E[X]−Cov(X,Z)Var(Z)−1(Z−E[Z]))ZT]=E[(X−E[X])ZT]−Cov(X,Z)Var(Z)−1E[(Z−E[Z])ZT]=E[XZT]−E[X]E[Z]T−Cov(X,Z)Var(Z)−1E[ZZT]+Cov(X,Z)Var(Z)−1E[Z]E[Z]T(18)
其中
E[XZT]=E[(X−E[X]+E(X))(Z−E[Z]+E(Z))T]=E[(X−E[X])(Z−E[Z])T]+E[X−E[X]]E[Z]T+E[X]E[Z−E[X]]T+E[X]E[Z]T=Cov(X,Z)+E[X]E[Z]T \begin{align*} E[XZ^{T}] &= E[(X-E[X]+E(X))(Z-E[Z]+E(Z))^{T}] \\ &= E[(X-E[X])(Z-E[Z])^{T}] +E[X-E[X]]E[Z]^{T}+E[X]E[Z-E[X]]^{T} + E[X]E[Z]^{T} \\ &= Cov(X,Z) + E[X]E[Z]^{T} \tag{19} \end{align*} E[XZT]=E[(X−E[X]+E(X))(Z−E[Z]+E(Z))T]=E[(X−E[X])(Z−E[Z])T]+E[X−E[X]]E[Z]T+E[X]E[Z−E[X]]T+E[X]E[Z]T=Cov(X,Z)+E[X]E[Z]T(19)
E[ZZT]=E[(Z−E[Z]+Z(Z))(Z−E[Z]+E(Z))T]=E[(Z−E[Z])(Z−E[Z])T]+E[Z−E[Z]]E[Z]T+E[Z]E[Z−E[Z]]T+E[Z]E[Z]T=Var(Z)+E[Z]E[Z]T \begin{align*} E[ZZ^{T}] &= E[(Z-E[Z]+Z(Z))(Z-E[Z]+E(Z))^{T}] \\ &= E[(Z-E[Z])(Z-E[Z])^{T}] +E[Z-E[Z]]E[Z]^{T}+E[Z]E[Z-E[Z]]^{T} + E[Z]E[Z]^{T} \\ &= Var(Z) + E[Z]E[Z]^{T} \tag{20} \end{align*} E[ZZT]=E[(Z−E[Z]+Z(Z))(Z−E[Z]+E(Z))T]=E[(Z−E[Z])(Z−E[Z])T]+E[Z−E[Z]]E[Z]T+E[Z]E[Z−E[Z]]T+E[Z]E[Z]T=Var(Z)+E[Z]E[Z]T(20)
式(19)(20)带入式(18),得
E[(X−E∗[X∣Z])ZT]=E[XZT]−E[X]E[Z]T−Cov(X,Z)Var(Z)−1E[ZZT]+Cov(X,Z)Var(Z)−1E[Z]E[Z]T=Cov(X,Z)+E[X]E[Z]T−E[X]E[Z]T−Cov(X,Z)Var(Z)−1(Var(Z)+E[Z]E[Z]T)+Cov(X,Z)Var(Z)−1E[Z]E[Z]T=Cov(X,Z)−Cov(X,Z)−Cov(X,Z)Var(Z)−1E[Z]E[Z]T+Cov(X,Z)Var(Z)−1E[Z]E[Z]T=0 \begin{align*} E[(X-E^{*}[X|Z])Z^{T}] &= E[XZ^{T}] -E[X]E[Z]^{T}-Cov(X,Z)Var(Z)^{-1} E[ZZ^{T}]+Cov(X,Z)Var(Z)^{-1}E[Z]E[Z]^{T} \\ &= Cov(X,Z) + E[X]E[Z]^{T} -E[X]E[Z]^{T}-Cov(X,Z)Var(Z)^{-1}(Var(Z) + E[Z]E[Z]^{T})+Cov(X,Z)Var(Z)^{-1}E[Z]E[Z]^{T} \\ &= Cov(X,Z) - Cov(X,Z) - Cov(X,Z)Var(Z)^{-1}E[Z]E[Z]^{T} + Cov(X,Z)Var(Z)^{-1}E[Z]E[Z]^{T} \\ &= \mathbf{0} \tag{21} \\ \end{align*} E[(X−E∗[X∣Z])ZT]=E[XZT]−E[X]E[Z]T−Cov(X,Z)Var(Z)−1E[ZZT]+Cov(X,Z)Var(Z)−1E[Z]E[Z]T=Cov(X,Z)+E[X]E[Z]T−E[X]E[Z]T−Cov(X,Z)Var(Z)−1(Var(Z)+E[Z]E[Z]T)+Cov(X,Z)Var(Z)−1E[Z]E[Z]T=Cov(X,Z)−Cov(X,Z)−Cov(X,Z)Var(Z)−1E[Z]E[Z]T+Cov(X,Z)Var(Z)−1E[Z]E[Z]T=0(21)
线性最小方差估计定义可知,E∗[X∣Z]E^{*}[X|Z]E∗[X∣Z]为观测向量ZZZ的线性组合,由式(17)和(21),E∗[X∣Z]E^{*}[X|Z]E∗[X∣Z]为观测向量ZZZ上的正交投影,即
E∗[X∣Z]=A∗Z+b∗ \begin{align*} E^{*}[X|Z] &= A^{*}Z+b^{*} \\ \end{align*} E∗[X∣Z]=A∗Z+b∗
必要性证毕
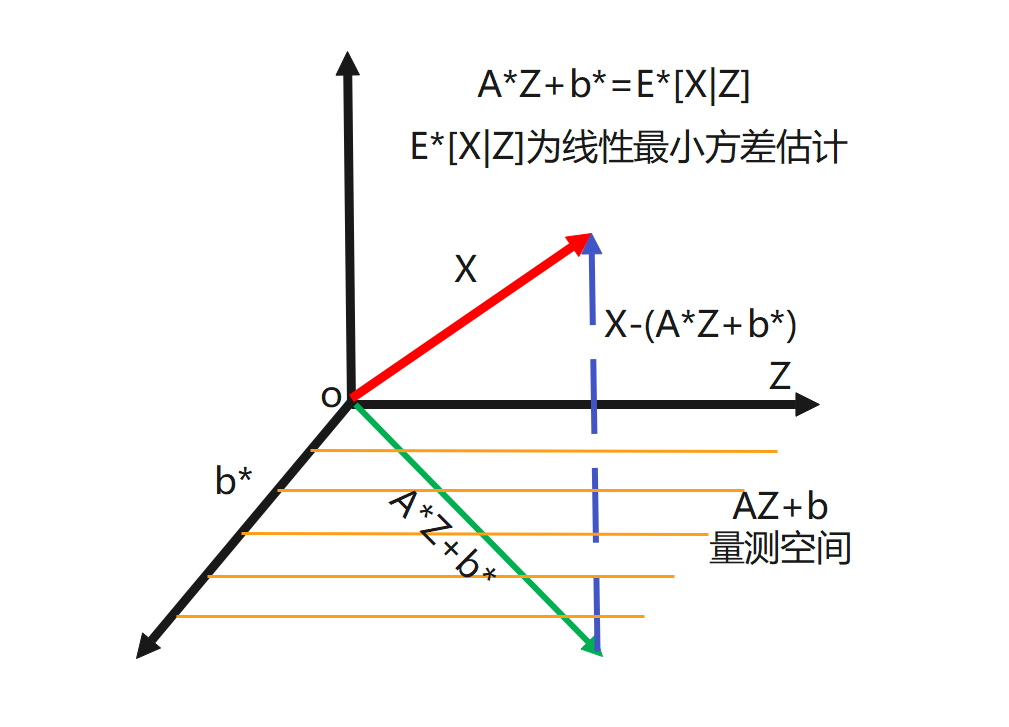
图1 正交投影定理几何示意图
如图1所示,从几何上理解为通过调整矩阵A∗A^{*}A∗和常数向量b∗b^{*}b∗,使得被估向量XXX落入量测空间AZ+bAZ+bAZ+b中并与其正交投影A∗Z+b∗A^{*}Z+b^{*}A∗Z+b∗重合,那么XXX在该量测空间上的正交投影A∗Z+b∗A^{*}Z+b^{*}A∗Z+b∗就是XXX在观测向量ZZZ条件下的线性最小方差估计,估计误差X−(A∗Z+b∗)X-(A^{*}Z+b^{*})X−(A∗Z+b∗)正交于量测空间AZ+bAZ+bAZ+b,正交于观测向量ZZZ,且估计误差的数学期望为0\mathbf{0}0。
推论
推论1
设XXX和YYY为具有二阶矩的随机向量,则XXX在ZZZ上的正交投影与XXX在ZZZ上的线性最小方差估计等价具有唯一性。
推论2
设XXX和YYY为具有二阶矩的随机向量,AAA为非随机矩阵,其列数等于XXX的维数,则
E∗[AX∣Z]=AE∗[X∣Z] \begin{align*} E^{*}[AX|Z] &= AE^{*}[X|Z] \tag{22} \end{align*} E∗[AX∣Z]=AE∗[X∣Z](22)
推论3
设XXX、YYY和ZZZ为具有二阶矩的随机向量,AAA和BBB为具有相应维数的非随机矩阵,则
E∗[AX+BY∣Z]=AE∗[X∣Z]+BE∗[Y∣Z] \begin{align*} E^{*}[AX+BY|Z] &= AE^{*}[X|Z] + BE^{*}[Y|Z] \tag{23} \end{align*} E∗[AX+BY∣Z]=AE∗[X∣Z]+BE∗[Y∣Z](23)
推论4
设XXX、Z1Z_{1}Z1和Z2Z_{2}Z2为具有二阶矩的随机向量,且Z=[Z1Z2]Z=\begin{bmatrix} Z_{1}\\ Z_{2} \end{bmatrix}Z=[Z1Z2],则
E∗[X~∣Z~2]=E[X~Z~2T]E[Z~2Z~2T]−1Z~2E∗[X∣Z]=E∗[X∣Z1]+E∗[X~∣Z~2]=E∗[X∣Z1]+E[X~Z~2T]E[Z~2Z~2T]−1Z~2 \begin{align*} E^{*}[\tilde{X}|\tilde{Z}{2}] &= E[\tilde{X}\tilde{Z}{2}^{T}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1}\tilde{Z}{2} \tag{24} \\ E^{*}[X|Z] &= E^{*}[X|Z{1}] + E^{*}[\tilde{X}|\tilde{Z}{2}] \\ &= E^{*}[X|Z{1}] + E[\tilde{X}\tilde{Z}{2}^{T}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1}\tilde{Z}{2} \tag{25} \\ \end{align*} E∗[X~∣Z~2]E∗[X∣Z]=E[X~Z~2T]E[Z~2Z~2T]−1Z~2=E∗[X∣Z1]+E∗[X~∣Z~2]=E∗[X∣Z1]+E[X~Z~2T]E[Z~2Z~2T]−1Z~2(24)(25)
其中X~\tilde{X}X~为XXX在Z1Z_{1}Z1条件下的线性最小方差估计误差,Z~2\tilde{Z}{2}Z~2为Z2Z{2}Z2在Z1Z_{1}Z1条件下的线性最小方差估计误差:
X~=X−E∗[X∣Z1]Z~2=Z2−E∗[Z2∣Z1] \begin{align*} \tilde{X} &= X- E^{*}[X|Z_{1}] \tag{26} \\ \tilde{Z}{2}&= Z{2}- E^{*}[Z_{2}|Z_{1}] \tag{27} \\ \end{align*} X~Z~2=X−E∗[X∣Z1]=Z2−E∗[Z2∣Z1](26)(27)
证明:
由E∗[X~∣Z~2]E^{*}[\tilde{X}|\tilde{Z}{2}]E∗[X~∣Z~2]是X~\tilde{X}X~在Z~2\tilde{Z}{2}Z~2条件下的线性最小方差估计:
E∗[X~∣Z~2]=E[X~]+Cov(X~,Z~2)Var(Z~2)−1[Z~2−E[Z~2]] \begin{align*} E^{*}[\tilde{X}|\tilde{Z}{2}] &= E[\tilde{X}]+Cov(\tilde{X},\tilde{Z}{2})Var(\tilde{Z}{2})^{-1}[\tilde{Z}{2}-E[\tilde{Z}_{2}]] \tag{28} \\ \end{align*} E∗[X~∣Z~2]=E[X~]+Cov(X~,Z~2)Var(Z~2)−1[Z~2−E[Z~2]](28)
又E[X~]=0E[\tilde{X}]=\mathbf{0}E[X~]=0,E[Z~2]=0E[\tilde{Z}{2}]=\mathbf{0}E[Z~2]=0,上式为
E∗[X~∣Z~2]=Cov(X~,Z~2)Var(Z~2)−1Z~2=(E[X~Z~2T]−E[X~]E[Z~2])(E[Z~2Z~2T]−E[Z~2]E[Z~2T])−1Z~2=E[X~Z~2T]E[Z~2Z~2T]−1Z~2 \begin{align*} E^{*}[\tilde{X}|\tilde{Z}{2}] &= Cov(\tilde{X},\tilde{Z}{2})Var(\tilde{Z}{2})^{-1}\tilde{Z}{2} \tag{29} \\ &= (E[\tilde{X}\tilde{Z}{2}^{T}]-E[\tilde{X}]E[\tilde{Z}{2}])(E[\tilde{Z}{2}\tilde{Z}{2}^{T}]-E[\tilde{Z}{2}]E[\tilde{Z}{2}^{T}])^{-1}\tilde{Z}{2} \\ &= E[\tilde{X}\tilde{Z}{2}^{T}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1}\tilde{Z}{2} \\ \end{align*} E∗[X~∣Z~2]=Cov(X~,Z~2)Var(Z~2)−1Z~2=(E[X~Z~2T]−E[X~]E[Z~2])(E[Z~2Z~2T]−E[Z~2]E[Z~2T])−1Z~2=E[X~Z~2T]E[Z~2Z~2T]−1Z~2(29)
式(24)证毕。
由于E∗[X∣Z1]E^{*}[X|Z_{1}]E∗[X∣Z1]和Z~2\tilde{Z}{2}Z~2均为Z1{Z}{1}Z1的线性组合,而Z1=[10]Z{Z}_{1}=\begin{bmatrix} 1&0 \end{bmatrix}ZZ1=[10]Z,故E∗[X∣Z]E^{*}[X|Z]E∗[X∣Z]也是ZZZ的线性组合。
又因为E∗[X∣Z1]E^{*}[X|Z_{1}]E∗[X∣Z1]的估计误差的数学期望为:
E[X−E∗[X∣Z]]=E[X−E∗[X∣Z]]=E[X−(E∗[X∣Z1]+E[X~Z~2]E[Z~2Z~2T]−1Z~2)]=E[X]−E[E∗[X∣Z1]]−E[X~Z~2T]E[Z~2Z~2T]−1E[Z~2]=E[X]−E[X]−0=0 \begin{align*} E[X-E^{*}[X|Z]] &= E[X-E^{*}[X|Z]] \tag{30} \\ &= E[X-(E^{*}[X|Z_{1}] + E[\tilde{X}\tilde{Z}{2}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1}\tilde{Z}{2})] \\ &= E[X]-E[E^{*}[X|Z_{1}]] - E[\tilde{X}\tilde{Z}{2}^{T}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1}E[\tilde{Z}{2}] \\ &= E[X]-E[X] - \mathbf{0} \\ &= \mathbf{0} \tag{31} \\ \end{align*} E[X−E∗[X∣Z]]=E[X−E∗[X∣Z]]=E[X−(E∗[X∣Z1]+E[X~Z~2]E[Z~2Z~2T]−1Z~2)]=E[X]−E[E∗[X∣Z1]]−E[X~Z~2T]E[Z~2Z~2T]−1E[Z~2]=E[X]−E[X]−0=0(30)(31)
式(31)满足正交投影定义中式(7)估计误差数学期望为0\mathbf{0}0。
接下来,只需证明E∗[X∣Z]E^{*}[X|Z]E∗[X∣Z]估计误差与ZZZ满足正交,即E∗[X∣Z]E^{*}[X|Z]E∗[X∣Z]为XXX在ZZZ上的正交投影:
E[(X−E∗[X∣Z])ZT]=E[(X−(E∗[X∣Z1]+E[X~Z~2T]E[Z~2Z~2T]−1Z~2))ZT]=E[(X−E∗[X∣Z1])ZT]−E[X~Z~2T]E[Z~2Z~2T]−1E[Z~2ZT]=E[X~ZT]−E[X~Z~2T]E[Z~2Z~2T]−1E[Z~2ZT]=E[X~[Z1TZ2T]]−E[X~Z~2T]E[Z~2Z~2T]−1E[Z~2[Z1TZ2T]]=[E[X~Z1T]E[X~Z2T]]−E[X~Z~2T]E[Z~2Z~2T]−1[E[Z~2Z1T]E[Z~2Z2T]] \begin{align*} E[(X-E^{*}[X|Z])Z^{T}] &= E[(X-(E^{*}[X|Z_{1}] + E[\tilde{X}\tilde{Z}{2}^{T}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1}\tilde{Z}{2}))Z^{T}] \\ &=E[(X-E^{*}[X|Z_{1}])Z^{T}] - E[\tilde{X}\tilde{Z}{2}^{T}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1}E[\tilde{Z}{2}Z^{T}] \\ &= E[\tilde{X}Z^{T}] - E[\tilde{X}\tilde{Z}{2}^{T}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1}E[\tilde{Z}{2}Z^{T}] \\ &= E[\tilde{X}\begin{bmatrix} Z_{1}^{T} &Z_{2}^{T} \end{bmatrix}] - E[\tilde{X}\tilde{Z}{2}^{T}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1}E[\tilde{Z}{2}\begin{bmatrix} Z_{1}^{T} &Z_{2}^{T} \end{bmatrix}] \\ &= \begin{bmatrix} E[\tilde{X}Z_{1}^{T}] &E[\tilde{X}Z_{2}^{T}] \end{bmatrix} - E[\tilde{X}\tilde{Z}{2}^{T}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1} \begin{bmatrix} E[\tilde{Z}{2}Z_{1}^{T}] &E[\tilde{Z}{2}Z{2}^{T}] \end{bmatrix} \tag{32} \\ \end{align*} E[(X−E∗[X∣Z])ZT]=E[(X−(E∗[X∣Z1]+E[X~Z~2T]E[Z~2Z~2T]−1Z~2))ZT]=E[(X−E∗[X∣Z1])ZT]−E[X~Z~2T]E[Z~2Z~2T]−1E[Z~2ZT]=E[X~ZT]−E[X~Z~2T]E[Z~2Z~2T]−1E[Z~2ZT]=E[X~[Z1TZ2T]]−E[X~Z~2T]E[Z~2Z~2T]−1E[Z~2[Z1TZ2T]]=[E[X~Z1T]E[X~Z2T]]−E[X~Z~2T]E[Z~2Z~2T]−1[E[Z~2Z1T]E[Z~2Z2T]](32)
由X~\tilde{X}X~、Z~2\tilde{Z}{2}Z~2与Z1{Z}{1}Z1正交,有:
E[X~Z1T]=0E[Z~2Z1T]=0 \begin{align*} E[\tilde{X}Z_{1}^{T}] &= \mathbf{0} \tag{33} \\ E[\tilde{Z}{2}Z{1}^{T}] &= \mathbf{0} \tag{34}\\ \end{align*} E[X~Z1T]E[Z~2Z1T]=0=0(33)(34)
又因为E∗[X∣Z1]E^{*}[X|Z_{1}]E∗[X∣Z1]与E∗[Z2∣Z1]E^{*}[Z_{2}|Z_{1}]E∗[Z2∣Z1]分别为XXX和Z2Z_{2}Z2在ZZZ上的正交投影,根据正交投影定义式(6),有:
E[X~(E∗[Z2∣Z1])T]=0E[Z~2(E∗[Z2∣Z1])T]=0 \begin{align*} E[\tilde{X}(E^{*}[Z_{2}|Z_{1}])^{T}] &= \mathbf{0} \tag{35} \\ E[\tilde{Z}{2}(E^{*}[Z{2}|Z_{1}])^{T}] &= \mathbf{0} \tag{36}\\ \end{align*} E[X~(E∗[Z2∣Z1])T]E[Z~2(E∗[Z2∣Z1])T]=0=0(35)(36)
于是由式(27)(35)(36),得:
E[X~Z2T]=E[X~(Z~2+E∗[Z2∣Z1])T]=E[X~Z~2T]+E[X~(E∗[Z2∣Z1])T]=E[X~Z~2T]E[Z~2Z2T]=E[Z~2(Z~2+E∗[Z2∣Z1])T]=E[Z~2Z~2T]+E[Z~2(E∗[Z2∣Z1])T]=E[Z~2Z~2T] \begin{align*} E[\tilde{X}Z_{2}^{T}] &= E[\tilde{X}(\tilde{Z}{2}+E^{*}[Z{2}|Z_{1}])^{T}] \\ &= E[\tilde{X}\tilde{Z}{2}^{T}]+E[\tilde{X}(E^{*}[Z{2}|Z_{1}])^{T}] \\ &= E[\tilde{X}\tilde{Z}{2}^{T}] \tag{37} \\ E[\tilde{Z}{2}Z_{2}^{T}] &= E[\tilde{Z}{2}(\tilde{Z}{2}+E^{*}[Z_{2}|Z_{1}])^{T}] \\ &= E[\tilde{Z}{2}\tilde{Z}{2}^{T}]+E[\tilde{Z}{2}(E^{*}[Z{2}|Z_{1}])^{T}] \\ &= E[\tilde{Z}{2}\tilde{Z}{2}^{T}] \tag{38} \\ \end{align*} E[X~Z2T]E[Z~2Z2T]=E[X~(Z~2+E∗[Z2∣Z1])T]=E[X~Z~2T]+E[X~(E∗[Z2∣Z1])T]=E[X~Z~2T]=E[Z~2(Z~2+E∗[Z2∣Z1])T]=E[Z~2Z~2T]+E[Z~2(E∗[Z2∣Z1])T]=E[Z~2Z~2T](37)(38)
将式(34)(34)(37)(38)代入式(32),得:
E[(X−E∗[X∣Z])ZT]=[E[X~Z1T]E[X~Z2T]]−E[X~Z~2T]E[Z~2Z~2T]−1[E[Z~2Z1T]E[Z~2Z2T]]=[0E[X~Z~2T]]−E[X~Z~2T]E[Z~2Z~2T]−1[0E[Z~2Z~2T]]=[0E[X~Z~2T]]−[0E[X~Z~2T]]=[00]=0 \begin{align*} E[(X-E^{*}[X|Z])Z^{T}] &= \begin{bmatrix} E[\tilde{X}Z_{1}^{T}] &E[\tilde{X}Z_{2}^{T}] \end{bmatrix} - E[\tilde{X}\tilde{Z}{2}^{T}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1} \begin{bmatrix} E[\tilde{Z}{2}Z_{1}^{T}] &E[\tilde{Z}{2}Z{2}^{T}] \end{bmatrix} \\ &= \begin{bmatrix} \mathbf{0} &E[\tilde{X}\tilde{Z}{2}^{T}] \end{bmatrix} - E[\tilde{X}\tilde{Z}{2}^{T}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1}\begin{bmatrix} \mathbf{0} &E[\tilde{Z}{2}\tilde{Z}{2}^{T}] \end{bmatrix} \\ &= \begin{bmatrix} \mathbf{0} &E[\tilde{X}\tilde{Z}{2}^{T}] \end{bmatrix} - \begin{bmatrix} \mathbf{0} &E[\tilde{X}\tilde{Z}{2}^{T}] \end{bmatrix} \\ &= \begin{bmatrix} \mathbf{0} &\mathbf{0} \end{bmatrix} \\ &= \mathbf{0} \tag{39} \\ \end{align*} E[(X−E∗[X∣Z])ZT]=[E[X~Z1T]E[X~Z2T]]−E[X~Z~2T]E[Z~2Z~2T]−1[E[Z~2Z1T]E[Z~2Z2T]]=[0E[X~Z~2T]]−E[X~Z~2T]E[Z~2Z~2T]−1[0E[Z~2Z~2T]]=[0E[X~Z~2T]]−[0E[X~Z~2T]]=[00]=0(39)
以上证毕。
由式 (31)(39),式(25)中的E∗[X∣Z]E^{*}[X|Z]E∗[X∣Z]为XXX在ZZZ上的正交投影,即为XXX在ZZZ条件下的最小方差估计,将式(27)代入式(25),得
E∗[X∣Z]=E∗[X∣Z1]+E[X~Z~2T]E[Z~2Z~2T]−1(Z2−E∗[Z2∣Z1]) \begin{align*} E^{*}[X|Z] &= E^{*}[X|Z_{1}] + E[\tilde{X}\tilde{Z}{2}^{T}]E[\tilde{Z}{2}\tilde{Z}{2}^{T}]^{-1} (Z{2}- E^{*}[Z_{2}|Z_{1}]) \tag{40} \\ \end{align*} E∗[X∣Z]=E∗[X∣Z1]+E[X~Z~2T]E[Z~2Z~2T]−1(Z2−E∗[Z2∣Z1])(40)
推论4也被称为更新信息定理。
参考文献
1\] 《最优估计理论》,刘胜,张红梅著,2011,科学出版社。 \[2\] 《卡尔曼滤波与组合导航原理》第4版,秦永元,张洪越,汪叔华著,2021,西北工业大学出版社。