数学建模——遗传算法

1.概念

遗传算法（Genetic Algorithm，GA）是一种基于自然选择和遗传学原理的搜索算法，它通过模拟生物进化过程来解决优化问题。

1.术语解释：

1. 个体（Individual）

• 定义：在遗传算法中，一个"个体"代表一个可能的解决方案。它通常用一种编码方式表示，这种编码方式能够完整地描述问题的一个解。

• 例子 ：对于旅行商问题（TSP），一个个体可以是一个城市的排列，例如[1, 3, 2, 5, 4]，表示旅行商依次访问这些城市的路径。

2. 种群（Population）

• 定义：种群是由多个个体组成的集合。在遗传算法中，种群代表了问题的多个可能解的集合。

• 作用：种群的多样性是遗传算法能够有效搜索解空间的关键因素之一。通过种群中的个体之间的交叉和变异操作，算法可以探索更多的解空间。

• 例子：对于TSP问题，一个种群可能包含100个不同的城市路径，每个路径是一个个体。

3. 适应度（Fitness）

• 定义：适应度是一个衡量个体在问题中表现好坏的指标。适应度越高，表示该个体越接近最优解。

• 作用：适应度决定了个体在选择操作中被选中的概率。适应度高的个体有更高的概率被选中进入下一代，从而推动种群向更优解进化。

• 例子 ：在TSP问题中，适应度可以定义为路径长度的倒数，即fitness = 1 / path_length。路径越短，适应度越高。

4. 适应度函数（Fitness Function

• 定义：适应度函数是一个计算个体适应度的函数。它根据问题的目标，将个体的编码映射为一个适应度值。

• 作用：适应度函数是遗传算法的核心部分，它决定了算法的优化方向。通过适应度函数，算法可以评估每个个体的质量，并据此进行选择、交叉和变异操作。

5. 染色体（Chromosome）

• 定义：染色体是遗传算法中用来表示个体的编码形式。它包含了个体的所有信息，通常是一个字符串或数组。

• 作用：染色体是遗传算法进行交叉和变异操作的基础。通过操作染色体，算法可以生成新的个体。

• 例子 ：在TSP问题中，染色体可以是一个城市的排列，例如[1, 3, 2, 5, 4]。

6. 基因（Gene）

• 定义：基因是染色体上的一个基本单元，它表示个体的一个特征或属性。

• 作用：基因是遗传算法中最小的操作单位。通过改变基因的值，可以改变个体的特征，从而影响个体的适应度。

• 例子 ：在TSP问题中，基因可以是一个城市的编号，例如1、2、3等。

7. 遗传（Genetics）

• 定义：遗传是指通过选择、交叉和变异操作，将种群中的个体的基因传递到下一代的过程。

• 作用：遗传操作是遗传算法的核心机制，通过模拟生物进化过程，算法能够逐步优化种群中的个体，最终找到最优解。

• 主要操作：

  • 选择（Selection）：根据适应度函数选择适应度高的个体进入下一代。

  • 交叉（Crossover）：将两个父代个体的部分基因片段交换，生成新的子代个体。

  • 变异（Mutation）：对个体的基因进行随机改变，引入新的遗传变异，增加种群的多样性。

省流版：

|-----------|-------------------------|-------------------------|
| 名词 | 含义 | 解释（以TSP问题为例） |
| 个体 | 一个可能的解。 | 所有城市的一种排列方式 |
| 种群 | 多个个体的集合。 | 很多种排列方式的合集 |
| 适应度 | 衡量个体好坏的指标。 | 判定排列方式好坏的指标 |
| 适应度函数 | 计算适应度的函数。 | 计算指标的函数 |
| 染色体 | 表示个体的编码形式。 | 排列形式例如[1, 3, 2, 5, 4] |
| 基因 | 染色体上的基本单元。 | 例如[1, 3, 2, 5, 4]种的1 |
| 遗传 | 通过选择、交叉和变异操作，将基因传递到下一代。 | |

2.编码方式

编码方式与实际问题有很大关系

1.整数编码

• 定义：将问题的解表示为整数序列。

• 适用场景 ：适用于组合优化问题，如旅行商问题（TSP），01背包问题。

• 优点：直接表示问题的解，容易理解，且能够保持解的合法性。

• 缺点：交叉和变异操作需要特别设计，以避免生成非法解。

• 例子：对于TSP问题，假设城市编号为1到5，一个可能的路径可以表示为：

  • [1, 3, 2, 5, 4]

2.二进制编码

• 定义：将问题的解表示为二进制字符串。

• 适用场景 ：适用于参数优化问题，尤其是连续变量的优化问题。比如要求解y=x在[0，30]的最大值

• 优点：编码简单，遗传操作（如交叉和变异）容易实现。

• 缺点：对于复杂的组合优化问题（如TSP），二进制编码可能导致解的非法性（即生成的解不符合问题的约束条件）。

• 例子：对于一个简单的优化问题，假设我们需要优化一个参数 x，其取值范围为 [0,15]，可以用4位二进制数表示，如：

  • x=5 → 0101

  • x=13 → 1101

3. 实数编码

• 定义：将问题的解表示为实数序列。

• 适用场景：适用于连续变量的优化问题。

• 优点：能够直接表示问题的解，适用于连续变量的优化。

• 缺点：需要设计合适的交叉和变异操作，以保持解的有效性。

• 例子：对于一个优化问题，假设需要优化两个参数 x 和 y，其取值范围分别为 [0,10] 和 [0,20]，一个可能的解可以表示为：

  • [3.5, 7.2]

3.遗传算法

在实际自然环境中，生物产生后代要经历遗传和变异的过程，遗传就是继承一部分父母的特性，变异就是还会有一部分新的变化，产生的后代当然有好有坏

自然选择（Natural selection ）指生物在生存斗争中适者生存、不适者被淘汰的现象，最初由C·R·达尔文提出。其实就是留下适应环境的变异，淘汰不适用环境的变异

1.选择

在遗传算法中，选择（Selection） 是一个关键步骤，其目的是根据个体的适应度（fitness）**从当前种群中选择出一些个体，用于生成下一代种群。**选择过程的核心思想是：适应度高的个体有更高的概率被选中，从而推动种群向更优解进化。选择过程模拟了自然选择中的"适者生存"原则。

|-------------------------------------|-----------------------------------------------------------------------|----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|---------------------------------------------------------------------------------|
| 轮盘赌选择（Roulette Wheel Selection） | 轮盘赌选择是最常用的选择方法之一。它的基本思想是：根据每个个体的适应度计算其被选中的概率，适应度高的个体被选中的概率更大。 | 具体步骤： 1. 计算适应度 ：计算每个个体的适应度 。 2. 计算总适应度 ：计算种群中所有个体的总适应度 。 3. 计算选择概率：每个个体被选中的概率 Pi​ 为： 4. 生成随机数：生成一个随机数 r（范围在0到1之间）。 5. 选择个体 ：根据随机数 r 和累积概率 选择个体。具体来说，找到满足 的个体 k。 | 优点： * 实现简单，计算效率高。 * 能够很好地反映个体的适应度差异。 缺点： * 如果种群中存在适应度极高的个体，可能会导致选择压力过大，使算法过早收敛。 |
| 锦标赛选择（Tournament Selection） | 锦标赛选择是一种简单而有效的选择方法。它的基本思想是：随机选择若干个体（称为"锦标赛规模"），从中选择适应度最高的个体进入下一代。 | 具体步骤： 1. 随机选择个体：从种群中随机选择 k 个个体（k 是锦标赛规模，通常为2或3）。 2. 比较适应度：比较这 k 个个体的适应度。 3. 选择最优个体：选择适应度最高的个体进入下一代。 | 优点： * 实现简单，计算效率高。 * 选择压力可以通过调整锦标赛规模 k 来控制。 缺点： * 如果 k 太大，可能会导致选择压力过大，使算法过早收敛。 |
| 排名选择（Rank Selection） | 排名选择是一种基于个体在种群中的排名来选择个体的方法。它的基本思想是：根据个体的排名计算选择概率，而不是直接根据适应度。 | 具体步骤： 1.根据排名赋予选择概率，可以自定义每一个排名的概率也可以用函数对应 2.然后类似轮盘赌生成随机数进行选择 | 优点： * 可以避免适应度极高的个体对选择过程的主导作用。 * 选择压力可以通过调整指数公式来控制或者自定义。 缺点： * 实现相对复杂，计算效率略低。 |

简单来说轮盘赌用的比较多，就是根据适应度算概率来抽奖（使用最多）

锦标赛就是抽几个样本选择适应度最高的几个（似乎容易漏掉最佳个体）

排名选择就是按适应度排名算概率来抽奖（可以避免主导效果）

---

选择出优势个体就可以遗传产生下一代了

常见的步骤有交叉和变异

2.交叉

对于二进制编码的染色体来说只需要做一下交叉就行

1. 单点交叉（Single-point Crossover）

• 定义：随机选择一个交叉点，将两个父代个体在该点处的基因片段进行交换。

• 步骤：

  1. 随机选择一个交叉点 k。

  2. 交换两个父代个体从交叉点 k 开始的基因片段。

• 例子：

  • 父代1：[1, 2, 3, 4, 5]

  • 父代2：[6, 7, 8, 9, 10]

  • 交叉点：2

  • 子代1：[1, 2| 8, 9, 10]

  • 子代2：[6, 7| 3, 4, 5]

2. 多点交叉（Multi-point Crossover）

• 定义：随机选择多个交叉点，将两个父代个体在这些点处的基因片段进行交换。

• 步骤：

  1. 随机选择多个交叉点 k1​,k2​,...,kn​。

  2. 交换两个父代个体在这些交叉点之间的基因片段。

• 例子：

  • 父代1：[1, 2| 3, 4, 5| 6, 7]

  • 父代2：[8, 9| 10, 11, 12| 13, 14]

  • 交叉点：2和5

  • 子代1：[1, 2| 10, 11, 12| 6, 7]

  • 子代2：[8, 9| 3, 4, 5| 13, 14]

这个方法有局限性，生物学中染色体对应位置基因一样才可以直接交叉。这里也是，当交叉后结果依然可行才能继续。

旅行商问题中，染色体是城市顺序，每一个染色体之间同样位置的基因不是一样的，如果直接交换就会导致城市重复，

比如：

• 父代1：[1, 2, 3, 4, 5]

• 父代2：[2, 1, 5, 4, 3]假如把父代2中间三位复制上去就变成[1, 1, 5, 4, 5]显然有问题

deepseek回答：

以下是几种解决城市重复问题的常用交叉方法，专为排列编码设计：

1. 部分匹配交叉 (Partially Matched Crossover - PMX)

   • 原理： 随机选择两个交叉点，交换两个父代个体在这两点之间的片段。交换会导致片段外的城市出现重复。为了解决这个问题，PMX建立一个映射关系：交换片段中父代1的城市对应父代2的城市，反之亦然。

   • 步骤：

     1. 随机选择两个交叉点（起点和终点），定义交叉段。

     2. 将父代1的交叉段复制到子代1的对应位置。

     3. 将父代2的交叉段复制到子代2的对应位置。

     4. 解决冲突（关键）：

        • 对于子代1中交叉段之外的位置：

          • 如果父代2在该位置的城市不在子代1的交叉段中，则直接复制到子代1的对应位置。

          • 如果父代2在该位置的城市在 子代1的交叉段中（即冲突），则查找该城市在父代1交叉段中的对应城市（根据步骤2建立的映射），并将这个对应城市放入子代1的该位置。如果这个对应城市也冲突，则继续按映射关系查找，直到找到一个不在子代1当前交叉段中的城市，然后放入。

        • 同理处理子代2（使用父代1的数据和映射关系）。

   • 优点： 能较好地保留父代的顺序和位置信息。

   • 缺点： 实现相对复杂，映射查找可能需要递归或循环。

   • 确实不好理解，这里备一张我自己的理解图

2. 顺序交叉 (Order Crossover - OX)

   • 原理： 随机选择两个交叉点，从一个父代复制两个交叉点之间的片段到子代。子代剩余位置的城市顺序由另一个父代决定，跳过已复制的城市。

   • 步骤 (生成一个子代)：

     1. 随机选择两个交叉点（起点和终点），定义交叉段。

     2. 将父代1的交叉段复制到子代的相同位置。

     3. 从父代2的第二个交叉点之后开始（循环到开头），按顺序列出父代2中不包含在子代已复制片段中的所有城市。

     4. 从子代的第二个交叉点之后开始（循环到开头），按步骤3列出的顺序，将这些城市依次填入子代的空位。

   • 优点： 实现相对简单，能较好地保留父代的相对顺序。

   • 缺点： 位置信息保留不如PMX。

   • 这里也是说的很复杂，说白了就是从一个父代截取一段给子代，剩余部分的顺序由另一个父代决定

还有很多交叉方式这里就不列举了，因为用的不多

3.变异

在遗传算法中，变异（Mutation） 是一个关键操作，它通过随机改变个体的某些基因来引入新的遗传变异，从而增加种群的多样性。这种多样性有助于算法避免陷入局部最优解，提高全局搜索能力。以下是几种常见的变异方法及其具体实现：（比较好理解就不做图示了）

常见的变异方法

1. 交换变异（Swap Mutation）

• 定义：随机选择路径中的两个城市，交换它们的位置。

• 适用场景：适用于排列编码（如TSP问题）。

• 步骤：

  1. 随机选择路径中的两个不同位置。

  2. 交换这两个位置上的城市。

• 例子：

  • 原路径：[1, 3, 2, 5, 4]

  • 选择位置1和3：

    • 位置1：3

    • 位置3：5

  • 交换后路径：[1, 5, 2, 3, 4]

2. 插入变异（Insert Mutation）

• 定义：随机选择路径中的一个城市，将其从当前位置移除并插入到另一个随机位置。

• 适用场景：适用于排列编码（如TSP问题）。

• 步骤：

  1. 随机选择路径中的一个城市。

  2. 随机选择一个新的插入位置。

  3. 将该城市从当前位置移除并插入到新位置。

• 例子：

  • 原路径：[1, 3, 2, 5, 4]

  • 选择城市5（位置3）插入到位置2：

    • 移除5后路径：[1, 3, 2, 4]

    • 插入后路径：[1, 5, 3, 2, 4]

3. 倒序变异（Inversion Mutation）

• 定义：随机选择路径中的两个位置之间的基因片段，并将其倒序。

• 适用场景：适用于排列编码（如TSP问题）。

• 步骤：

  1. 随机选择路径中的两个位置。

  2. 将这两个位置之间的基因片段倒序。

• 例子：

  • 原路径：[1, 3, 2, 5, 4]

  • 选择位置1到3之间的片段：[3, 2]

  • 倒序后片段：[2, 3]

  • 变异后路径：[1, 2, 3, 5, 4]

2.代码流程

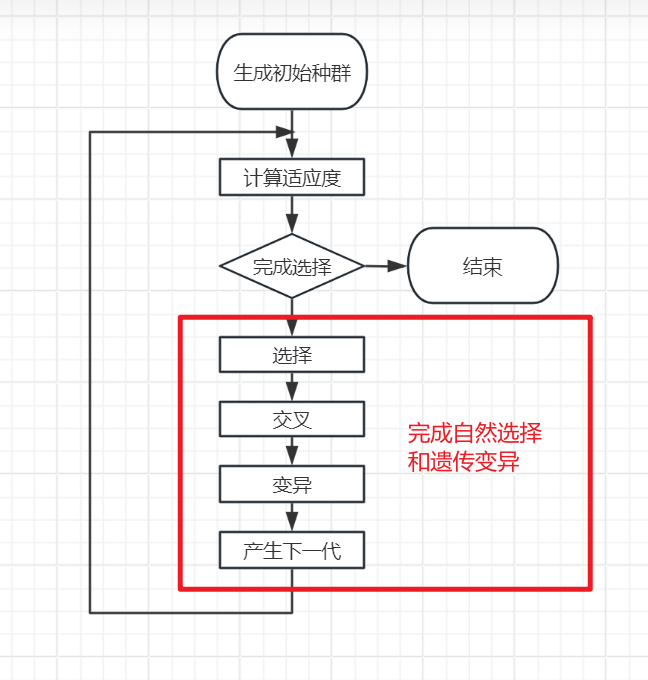
虽然步骤不多但是真做起来还是比较复杂的

主要还是交叉那一块比较复杂，需要根据题目选择合适的交叉方法