PyTorch基础(使用Numpy实现机器学习)

使用Numpy实现机器学习

前面已经介绍了Numpy、Tensor的基础内容，对如何使用Numpy、Tensor操作数组有

了一定认识。为了加深大家对使用PyTorch完成机器学习、深度学习的理解，本章剩余章

节将分别用Numpy、Tensor、autograd、nn及optimal来实现同一个机器学习任务，比较它

们之间的异同及各自优缺点，从而使读者加深对PyTorch的理解。

首先，我们用最原始的Numpy实现有关回归的一个机器学习任务，不用PyTorch中的

包或类。这种方法代码可能多一点，但每一步都是透明的，有利于理解每步的工作原理。

主要步骤包括：

首先，给出一个数组x，然后基于表达式y=3x2+2y=3x^2+2y=3x2+2加上一些噪音数据到达另一组数

据y。

然后，构建一个机器学习模型，学习表达式y=wx2+by=wx^{2}+by=wx2+b 的两个参数w、b。利用数组x，y

的数据为训练数据。

最后，采用梯度梯度下降法，通过多次迭代，学习到w、b的值。

以下为具体步骤：

1）导入需要的库。

python 复制代码

# -*- coding: utf-8 -*-
import numpy as np
%matplotlib inline
from matplotlib import pyplot as plt

2）生成输入数据x及目标数据y。

设置随机数种子，生成同一个份数据，以便用多种方法进行比较。

python 复制代码

np.random.seed(100)
x = np.linspace(-1, 1, 100).reshape(100,1)
y = 3*np.power(x, 2) +2+ 0.2*np.random.rand(x.size).reshape(100,1)

3）查看x、y数据分布情况。

python 复制代码

# 画图
plt.scatter(x, y)
plt.show()

完整代码

python 复制代码

import numpy as np

from matplotlib import pyplot as plt
np.random.seed(100)
x=np.linspace(-1,1,100).reshape(100,1)
y=3*np.power(x,2)+2+0.2*np.random.rand(x.size).reshape(100,1)

plt.scatter(x,y)
plt.show()

运行结果如图2-11所示。

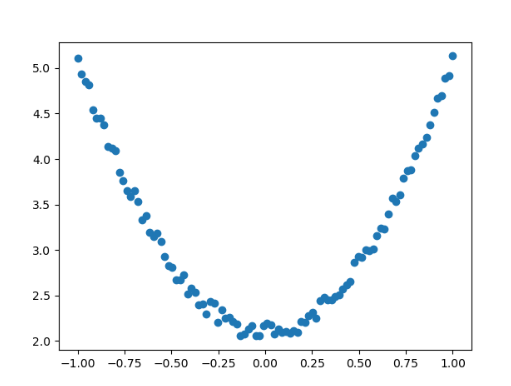
4）初始化权重参数。

python 复制代码

# 随机初始化参数
w1 = np.random.rand(1,1)
b1 = np.random.rand(1,1)

5）训练模型。

定义损失函数，假设批量大小为100：
Loss=12∑i=1100(wxi2+b−yi)2\text{Loss} = \frac{1}{2} \sum_{i=1}^{100} (w x_i^2 + b - y_i)^2Loss=21i=1∑100(wxi2+b−yi)2

对损失函数求导：
∂Loss∂w=∑i=1100(wxi2+b−yi)xi2\frac{\partial \text{Loss}}{\partial w} = \sum_{i=1}^{100} (w x_i^2 + b - y_i) x_i^2∂w∂Loss=i=1∑100(wxi2+b−yi)xi2

∂Loss∂b=∑i=1100(wxi2+b−yi)\frac{\partial \mathrm{Loss}}{\partial b}=\sum_{i=1}^{100}\left(w x_{i}^{2}+b-y_{i}\right)∂b∂Loss=∑i=1100(wxi2+b−yi)

利用梯度下降法学习参数，学习率为lr。

$( w_{1\^-} = lr \* \\frac{\\partial \\text{Loss}}{\\partial w} )$

$( b_{1\^-} = lr \* \\frac{\\partial \\text{Loss}}{\\partial b} )$

用代码实现上面这些表达式：

python 复制代码

import numpy as np
from matplotlib import pyplot as plt

lr=0.001 #学习率
#随机初始化参数
w1=np.random.rand(1,1)
b1=np.random.rand(1,1)
x = np.linspace(-1, 1, 100).reshape(100,1)
y = 3*np.power(x, 2) +2+ 0.2*np.random.rand(x.size).reshape(100,1)
for i in range(800):
    #前向传播
    y_pred=np.power(x,2)*w1+b1
    #定义损失函数
    loss=0.5*(y_pred-y)**2
    loss=loss.sum()
    #计算梯度
    grad_w=np.sum((y_pred-y)*np.power(x,2))
    grad_b=np.sum((y_pred-y))
    #使用梯度下降法，是loss最小
    w1-=lr*grad_w
    b1-=lr*grad_b

plt.plot(x,y_pred,'r-',label='predict')
plt.scatter(x,y,color='blue',marker='o',label='true')
plt.xlim(-1,1)
plt.ylim(2,6)
plt.legend()
plt.show()
print(w1,b1)

运行效果

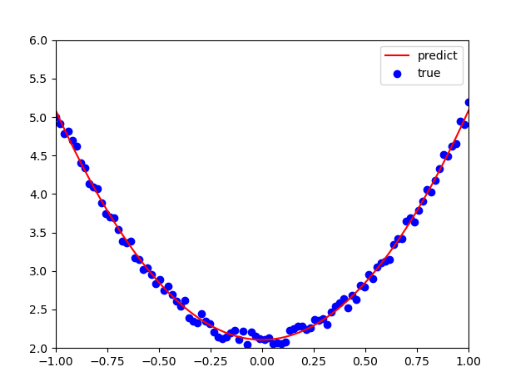
从结果看来，学习效果还是比较理想的。