摘要
通过增加测试时计算量使大型语言模型(LLMs)提升输出效果,是构建能基于开放自然语言自主改进的通用智能体的重要步骤。本文研究LLMs推理阶段计算量的扩展规律,重点回答以下问题:若允许LLM使用固定但可观的推理阶段计算量,其能在具有挑战性的提示上提升多少性能?回答该问题不仅对LLMs\mathbf{LLMs}LLMs的可实现性能有启示,还影响LLMs预训练的未来方向以及如何权衡推理阶段与预训练阶段的计算资源。尽管该问题重要,但鲜有研究尝试理解各种测试时推理方法的扩展行为。此外,现有工作大多对这些策略给出了负面结果。本文分析两种扩展测试时计算量的主要机制:(1)基于密集过程验证器奖励模型进行搜索;(2)根据测试时提示动态调整模型对响应的概率分布。我们发现,两种情况下不同测试时计算量扩展方法的有效性均高度依赖提示的难度。这一观察促使我们采用"计算最优"扩展策略,即根据每个提示动态分配测试时计算量以实现最有效利用。使用该计算最优策略,相比最佳N选1(best-of-N)基线,测试时计算量扩展效率可提升超过4倍。此外,在FLOPs匹配的评估中,我们发现对于某些问题,当较小基础模型达到一定非零成功率时,测试时计算量可超越14倍参数量的更大模型。
1 引言
人类在面对困难问题时往往会花更长时间思考,以可靠地改进决策[9, 17, 18]。我们能否为当前的大型语言模型(LLMs)赋予类似能力?更具体地说,对于具有挑战性的输入查询,能否使语言模型在测试时最有效地利用额外计算量,以提高响应的准确性?理论上,通过在测试时增加计算量,LLM应能超越其训练时的能力。此外,这种测试时能力还可能为自主智能体和推理任务开辟新途径[28, 34, 47]。例如,若预训练模型规模可与推理阶段计算量进行权衡,则可在需要较小设备端模型的场景中替代数据中心级LLM。通过额外推理计算自动生成改进的模型输出,也为实现通用自改进算法提供了路径,该算法可在减少人工监督的情况下运行。
此前研究测试时计算量的工作结果不一。一方面,部分研究表明当前LLM可通过测试时计算量提升输出[4, 8, 23, 30, 48];另一方面,其他工作显示这些方法在数学推理等复杂任务上的效果仍非常有限[15, 37, 43],尽管推理问题通常只需基于现有知识进行推断,而非获取新知识。这类矛盾结论促使需要系统分析不同测试时计算量扩展方法。
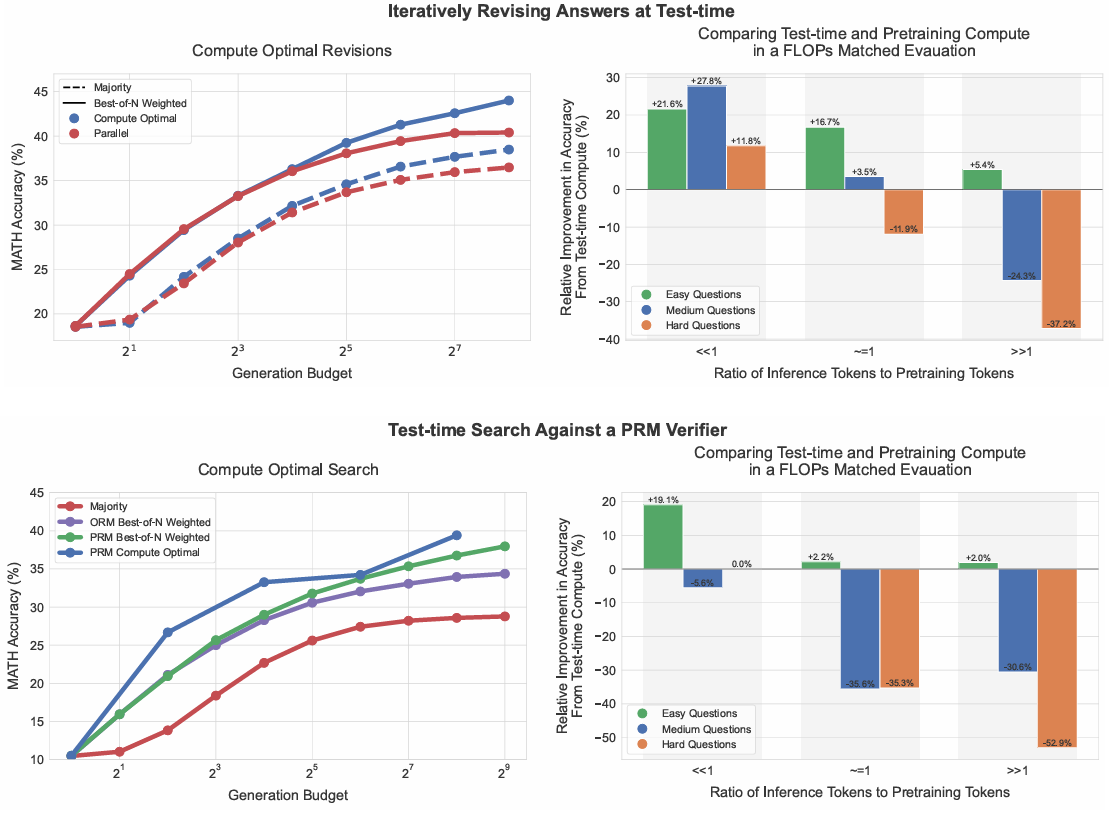
图1 | 主要结果总结。左:迭代自优化(即修订)与搜索的计算最优扩展。左侧比较了PaLM 2-S*修订模型的计算最优扩展策略与基线在修订场景(上)和PRM搜索场景(下)的表现。可见在修订场景中,标准最佳N选1(如"并行")与计算最优扩展的差距逐渐扩大,计算最优扩展可用4倍更少的测试计算量超越最佳N选1。类似地,在PRM搜索场景中,计算最优扩展早期显著优于最佳N选1,部分点上用4倍更少计算量即可接近最佳N选1的表现。详见第5、6节。右:测试时计算量与模型参数量扩展的对比。我们比较了计算最优测试时扩展的PaLM 2-Sˉ\bar{\mathrm{S}}Sˉ*模型与无额外测试时计算量的∼\sim∼ 14倍更大预训练模型(如贪心采样)的性能。考虑预训练X token、推理Y token的场景。训练更大模型会等比例增加两者的FLOPs需求。若为较小模型分配额外测试时计算量以匹配更大模型的FLOPs需求,其准确性如何?可见在修订场景(上),当Y≪XY \ll XY≪X时,测试时计算量通常优于额外预训练。但随着推理与预训练token比例增加,测试时计算量在简单问题上仍更优;而困难问题上预训练更优。PRM搜索场景(下)也呈现类似趋势。详见第7节。
我们关注理解扩展测试时计算量的收益。最简单且研究最充分的方法是最佳N选1采样:从基础LLM"并行"采样N个输出,并选择经学习验证器或奖励模型评分最高的结果[7,22]。但该方法并非唯一利用测试时计算量改进LLM的途径。通过修改响应的生成分布(例如让基础模型"顺序"修订原始响应[28]),或调整验证器的使用方式(例如训练基于过程的密集验证器[22,45]并基于此搜索),可大幅提高测试时计算量的扩展能力,如本文所示。
为理解扩展测试时计算量的收益,我们在具有挑战性的MATH[13]基准上开展实验,使用专门微调的PaLM-2[3]模型进行错误答案修订[28](如改进生成分布;第6节)或通过基于过程的奖励模型(PRM)[22,45]验证答案步骤的正确性(第5节)。两种方法均表明,特定测试时计算策略的有效性高度依赖具体问题的性质和基础LLM。例如,对于基础LLM已能生成合理响应的简单问题,允许模型通过预测N个修订序列迭代优化初始答案(即修改生成分布),可能比并行采样N个独立响应更有效利用测试时计算量。另一方面,对于可能需要探索多种高层解题策略的困难问题,并行重新采样独立响应或基于过程奖励模型的树搜索,可能是更有效的测试时计算利用方式。这一发现表明需要部署自适应的"计算最优"策略来扩展测试时计算量,即根据提示动态选择测试时计算利用方式,以实现最佳效果。我们还表明,基于基础LLM视角的问题难度(第4节)可预测测试时计算量的有效性,从而实际构建这种计算最优策略。通过计算最优扩展,修订和搜索场景下均可超越最佳N选1基线,同时仅使用约1/4的计算量(第5、6节)。
利用改进的测试时计算扩展策略,我们进一步探究测试时计算量在多大程度上可替代额外预训练。我们对比了较小模型加测试时计算量与14倍更大预训练模型的FLOPs匹配场景。发现对于简单、中等难度问题,甚至部分困难问题(取决于预训练和推理工作负载的具体条件),额外测试时计算量通常优于扩展预训练。这表明与其单纯扩展预训练,某些场景下预训练较小模型并应用测试时计算量更有效。但需注意,对于最具挑战性的问题,测试时计算量的收益非常有限,此时额外预训练计算量更有效,表明当前测试时计算扩展方法无法与预训练扩展完全等价。总体而言,这表明即使采用较简单的方法,扩展测试时计算量已可比扩展预训练更优,且随着测试时策略的成熟,收益将进一步提升。长远来看,这暗示未来可减少预训练FLOPs,增加推理阶段FLOPs。
2 测试时计算的统一视角:提议者与验证者
我们首先统一了利用测试时计算的方法,并分析了一些代表性技术。首先,我们从动态调整模型在给定提示下的预测分布这一角度,审视额外测试时计算的使用。理想情况下,测试时计算应修改分布,使生成结果优于直接从LLM采样。一般来说,诱导LLM分布修改有两种方式:(1)输入层:通过向给定提示添加额外标记,使LLM基于这些标记调整分布;(2)输出层:从标准语言模型采样多个候选,并对这些候选进行修正。换言之,我们可以通过修改LLM自身诱导的提议分布(使其优于单纯基于提示的条件分布),或使用事后验证器/评分器对输出进行修正。这一过程类似于从复杂目标分布中通过马尔可夫链蒙特卡洛(MCMC)[2]采样,但结合了简单的提议分布和评分函数。通过调整输入标记直接修改提议分布,以及使用验证器,构成了我们研究的两个独立方向。
修改提议分布。改进提议分布的一种方法是通过对抗强化学习(RL)的微调方法(如STaR或ReST,EM[35,50])直接优化模型在特定推理任务上的表现。需要注意的是,这些技术不依赖额外输入标记,而是通过微调模型来诱导更优的提议分布。相反,自我批判(self-critique)[4,8,23,30]等方法使模型在测试时通过迭代批判和修正自身输出,从而改进提议分布。由于直接提示现成模型无法有效实现测试时修正,我们专门微调模型在复杂推理场景中迭代修正答案。为此,我们采用基于最佳N选1(Best-of-N)引导改进的微调方法[28],利用在策略数据(on-policy data)进行微调。
优化验证器。在提议分布与验证器的抽象框架中,验证器用于从提议分布中聚合或选择最优答案。最典型的方式是使用最佳N选1采样:采样N个完整解决方案,然后通过验证器选择最优解[7]。但该方法可进一步改进,例如训练基于过程的验证器[22](即过程奖励模型,PRM),其预测解决方案中每一步的正确性,而非仅评估最终答案。利用这些逐步预测,我们可以在解决方案空间中执行树搜索,相比简单的最佳N选1[6,10,48],可能实现更高效、更有效的验证器搜索。
3 如何最优扩展测试时计算
基于对各类方法的统一分析,我们现在希望理解如何最有效地利用测试时计算来提升语言模型在给定提示下的性能。具体而言,我们试图回答以下问题:
问题设定
给定一个提示和测试时计算预算,我们需要在上述抽象框架下选择不同的测试时计算利用方式。不同方法对具体问题的有效性可能差异显著。如何为给定提示确定最有效的测试时计算利用方式?这种方法与直接使用更大的预训练模型相比效果如何?
无论是修正提议分布还是基于验证器搜索,均存在多个可调整的超参数以决定测试时计算预算的分配方式。例如,当使用微调后的修正模型作为提议分布、ORM作为验证器时,我们可以将全部测试时计算预算用于并行生成N个独立样本并执行最佳N选1,或按顺序生成N个修正版本并使用ORM选择最优答案,或在两者之间取得平衡。直觉上,我们可能认为"简单"问题更适合修正,因为模型的初始样本更可能接近正确方向,只需进一步细化;而困难问题可能需要探索不同的高层解题策略,因此并行独立采样多次可能更优。
对于验证器,我们还可选择不同的搜索算法(如束搜索、前瞻搜索、最佳N选1),其性能可能因验证器和提议分布的质量而异。更复杂的搜索程序可能在更难的问题上比简单的最佳N选1或多数投票基线更有效。
3.1 测试时计算最优扩展策略
因此,我们希望为给定问题选择最优的测试时计算预算分配方式。为此,对于任意利用测试时计算的方法(如本文的修正和验证器搜索,或其他方法),我们定义"测试时计算最优扩展策略"为:在给定提示下,通过调整超参数使测试时计算预算的分配能最大化性能收益的策略。形式化地,设Target(θ,N,q)\operatorname{Target}(\theta, N, q)Target(θ,N,q)为模型在给定提示qqq、测试时计算超参数θ\thetaθ和预算NNN时诱导的自然语言输出分布。我们希望选择超参数θ\thetaθ,使该分布在给定问题上的准确率最高。正式表述为:
θq,a∗(q)∗(N)=argmaxθ(Ey∼Target(θ,N,q)[1y=y∗(q)]),\begin{array}{r}{\boldsymbol{\theta}{q,a^{*}(q)}^{*}\big(N\big)=\operatorname*{arg max}{\boldsymbol{\theta}}\left(\mathbb{E}{\boldsymbol{y}\sim\operatorname*{Target}\left(\boldsymbol{\theta},N,q\right)}\left[\mathbb{1}{\boldsymbol{y}=\boldsymbol{y}^{*}(q)}\right]\right),}\end{array}θq,a∗(q)∗(N)=argmaxθ(Ey∼Target(θ,N,q)[1y=y∗(q)]),
其中y∗(q){\boldsymbol{y}}^{*}({\boldsymbol{q}})y∗(q)表示提示qqq的地面真实正确响应,θq,y∗(q)∗(N)\boldsymbol{\theta}_{q,y^{*}\left(q\right)}^{*}\big(N\big)θq,y∗(q)∗(N)表示在计算预算NNN下,针对问题qqq的最优测试时计算扩展策略。
3.2. 基于问题难度的计算最优扩展估计
为有效分析第2节中讨论的不同机制(如提议分布与验证器)的测试时扩展特性,我们将最优策略θq,y∗(q)∗(N)\boldsymbol{\theta}_{q,y^{*}\left(q\right)}^{*}\big(N\big)θq,y∗(q)∗(N)近似为提示的某个统计量的函数。该统计量估计了提示的难度。计算最优策略定义为该难度的函数。尽管这只是对式(1)中问题的近似解,我们发现它仍能显著提升性能,优于随机或均匀分配推理计算预算的基线策略。
我们的难度估计将给定问题划分为五个难度等级。通过验证集上的离散难度分类,我们可以为给定测试时计算预算估计θq,y∗(q)∗(N)\boldsymbol{\theta}_{q,y^{*}\left(q\right)}^{*}\big(N\big)θq,y∗(q)∗(N),并将该策略应用于测试集。具体而言,我们独立为每个难度等级选择性能最优的测试时计算策略。因此,问题难度作为设计计算最优策略的充分统计量。
定义问题难度。遵循Lightman等人[22]的方法,我们基于基础LLM定义问题难度。具体来说,我们将模型在测试集每个问题上的pass@1率(通过2048个样本估计)划分为五个分位数,分别对应递增的难度等级。我们发现,这种基于模型的难度分箱比MATH数据集中的手工标注难度更能预测测试时计算的有效性。
需注意,上述难度评估假设可访问地面真实正确性检查函数,而实际部署时我们无法知晓测试提示的答案。因此,基于难度的计算最优策略需首先评估问题难度,再利用对应策略解决。为此,我们通过模型预测的难度近似真实难度:对每个问题的2048个样本,基于学习验证器的平均最终答案得分(而非地面真实正确性)执行相同分箱程序。我们将此设定称为"模型预测难度",而依赖地面真实正确性的设定称为"oracle难度"。
尽管模型预测难度避免了依赖地面真实标签,但其评估仍需额外推理计算。不过,此一次性推理成本可包含在执行推理策略的总成本中(例如,使用验证器时,可复用相同推理计算进行搜索)。更一般地,这类似于强化学习中的探索-利用权衡:实际部署时需平衡评估难度与应用最优策略的计算开销。这是未来研究的关键方向(见第8节),而我们的实验为简化未考虑此成本,因我们目标仅是展示有效分配测试时计算的初步结果。
为避免使用同一测试集计算难度分箱和选择最优策略的混淆因素,我们对测试集的每个难度分箱采用两折交叉验证。在一折上选择性能最优的策略,并在另一折上评估该策略的性能,反之亦然,最终对两折结果取平均。
4 实验设置
我们首先概述实验设置,包括多种验证器设计选择和提议分布的分析,后续章节将呈现分析结果。
数据集。我们聚焦于模型已掌握所需基本知识、主要挑战在于从该知识中推导(复杂)推理的场景。为此,我们选择MATH[13]基准,该数据集包含高中竞赛级别的数学问题,难度范围广泛。所有实验均采用Lightman等人[22]使用的数据集划分:12k训练问题和500测试问题。
模型。我们使用PaLM 2-S*[3](Codey)基础模型进行分析。该模型代表了当代LLMs的典型能力,因此我们认为 findings可推广至类似模型。更重要的是,该模型在MATH上达到非零性能且未饱和,适合作为测试平台。
5 通过验证器扩展测试时计算
本节分析如何通过优化验证器尽可能有效地扩展测试时计算。我们研究基于过程验证器(PRM)的测试时搜索方法,并分析不同方法的测试时计算扩展特性。
5.1 训练适用于搜索的验证器
PRM训练。原始PRM训练[22,42]依赖人工标注数据。尽管Lightman等人[22]发布了PRM训练数据(PRM80Ok),但我们发现该数据效果有限。即使通过简单策略(如最佳N选1)也可轻易利用基于此数据训练的PRM。推测原因可能是该数据集的GPT-4生成样本与我们的PaLM 2模型存在分布偏移。为避免昂贵的人工标注,我们采用Wang等人[45]的方法,通过蒙特卡洛展开估计每步正确性,无需人工标签即可训练PRM。具体而言,PRM的每步预测对应基础模型采样策略的回报到值估计(reward-to-go),与近期工作[31,45]一致。我们还对比了ORM基线(附录F),但发现PRM始终更优。因此,本节所有搜索实验均使用PRM模型。PRM训练细节见附录D。
答案聚合。测试时,基于过程的验证器可对基础模型采样的多组解进行逐步评分。为通过PRM选择最佳N选1答案,需设计聚合函数将各答案的逐步评分整合为最终分数。具体实现如下:
逐步聚合。我们不采用乘积或最小值聚合[22,45],而是直接使用PRM对最后一步的预测作为整题分数。实验表明该方法在所有研究过的聚合方法中表现最佳(见附录E)。
答案间聚合。我们遵循Li等人[21]的"最佳N选1加权"策略,而非标准最佳N选1。该方法对所有具有相同最终答案的解进行边际化,选择总评分最高的最终答案。
5.2 基于PRM的搜索方法
我们通过搜索方法优化PRM在测试时的表现。研究三种从少样本提示的基础LLM采样输出的搜索策略(见附录G),图2为示意图。
最佳N选1加权。从基础LLM独立采样N个答案,根据PRM的最终答案评分选择最优解。
束搜索(Beam Search)。通过束搜索优化PRM的逐步预测。实现类似BFS-V[10,48],具体步骤如下:
- 采样N个初始预测作为解决方案的第一步
- 根据PRM的逐步回报到值估计(对应稀疏奖励设置下的总奖励)对生成步骤评分
- 保留前NM\frac{N}{M}MN个最高分步骤
- 对每个候选步骤采样M个下一步提案,得到总计N/M×MN{\big/}M\times MN/M×M个候选前缀,重复步骤2-4
搜索持续至解决方案结束或达到最大展开轮数(本实验设为40)。最终保留N个候选答案,通过最佳N选1加权选择最终答案。
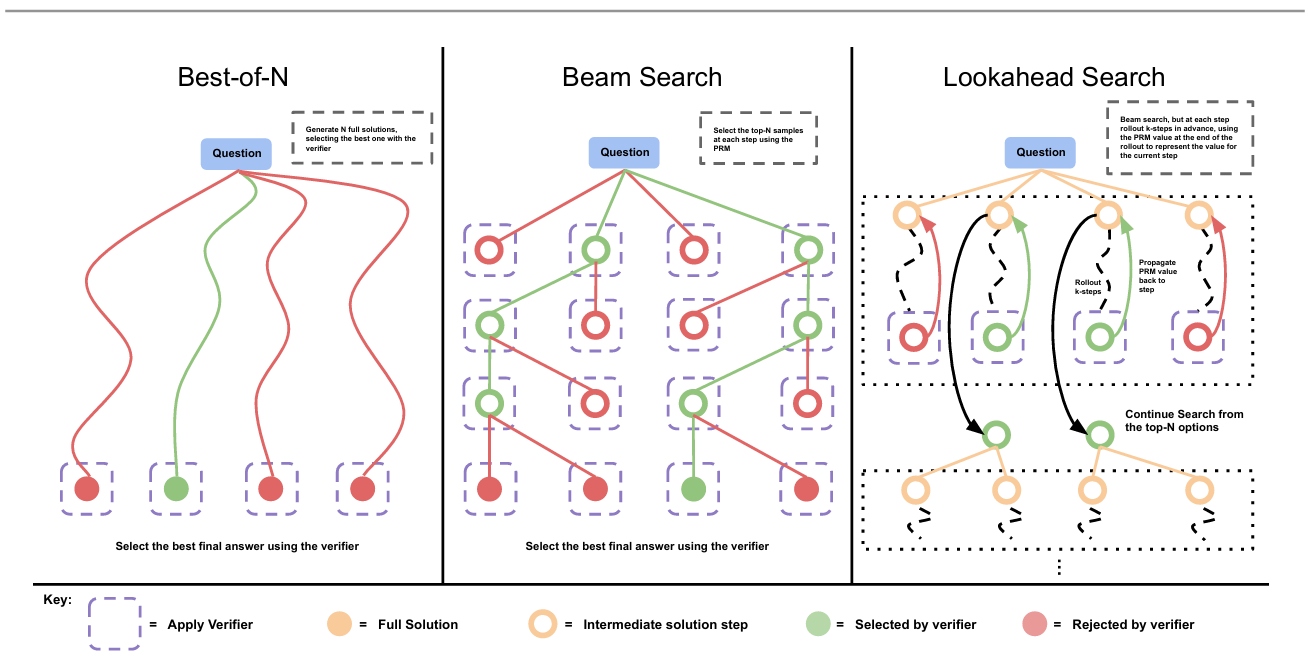
图2 | 不同PRM搜索方法对比。左:最佳N选1采样N个完整答案,根据PRM最终评分选择最优解。中:束搜索每步采样N个候选,根据PRM选择前M个继续搜索。右:前瞻搜索在束搜索基础上扩展,利用k步前瞻评估保留步骤,需更多计算。
前瞻搜索(Lookahead Search)。修改束搜索的步骤评估方式,通过前瞻展开提高PRM值估计的准确性。具体而言,在束搜索的每一步,不直接使用当前步骤的PRM评分选择候选,而是执行模拟展开:以温度0采样最多k步(若提前到达解终点则停止),使用展开末尾的PRM预测评分当前步骤。换言之,束搜索可视为前瞻搜索的特例(k=0)。若PRM准确,增加k可提高逐步值估计的准确性,但需额外计算。此版本前瞻搜索是MCTS[38]的特例,去除了MCTS中用于探索的随机元素(因PRM已训练完成且冻结),这些元素对值函数学习(已通过PRM完成)作用有限,测试时更需利用而非探索。因此,前瞻搜索可代表MCTS类方法在测试时的应用。
5.3 分析结果:验证器搜索的测试时扩展
本节比较不同搜索算法,并识别搜索方法的提示难度依赖型计算最优扩展策略。
搜索算法对比。我们首先扫描不同搜索设置。除标准最佳N选1外,扫描束搜索的两个主参数(束宽M和前瞻步数k)。在最大预算256下,扫描以下设置:
- 束宽设为N{\sqrt{N}}N 的束搜索,N为生成预算
- 固定束宽4的束搜索
- 对上述两种束搜索设置应用k=3的前瞻搜索
- 对设置1应用k=1的前瞻搜索
为公平比较生成预算,我们定义生成成本:基础LLM采样一个答案计为一次生成。束搜索和最佳N选1的生成预算分别对应束宽和N。前瞻搜索需额外计算:每步搜索需模拟k步前瞻,因此成本定义为N×(k+1)N\times(k+1)N×(k+1)次采样。
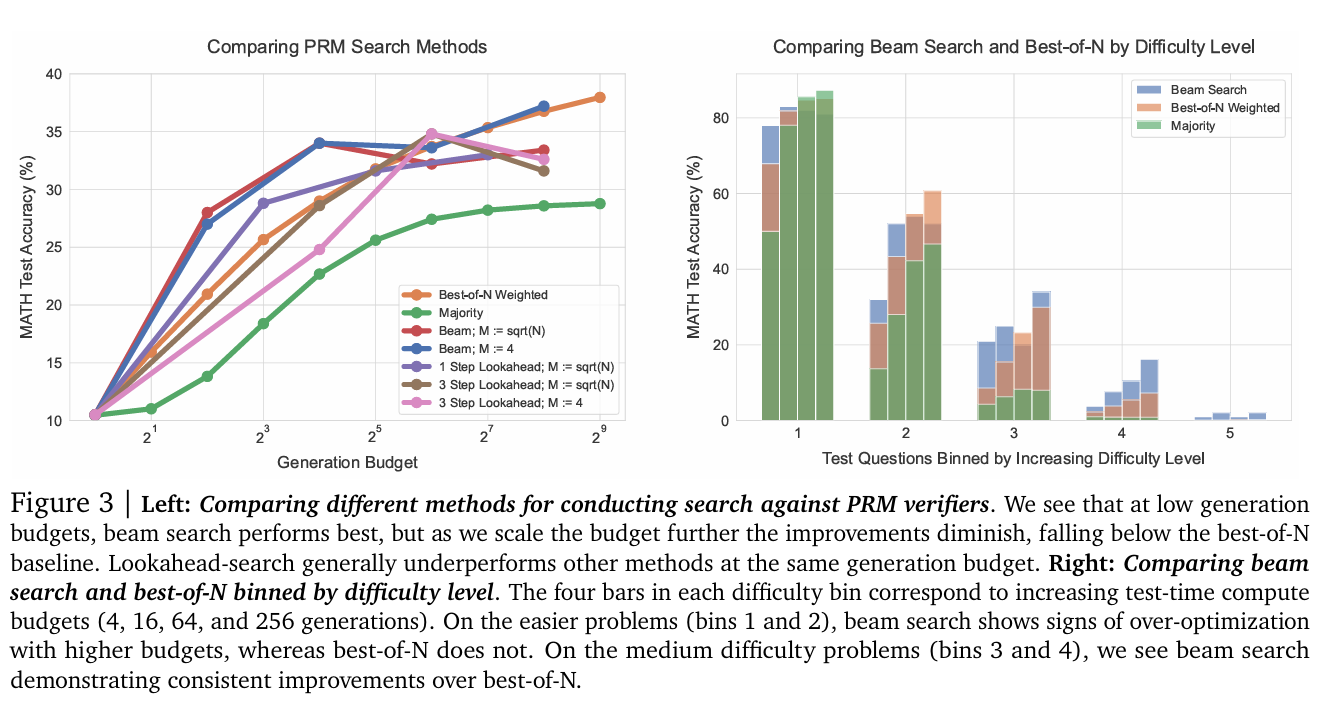
结果。如图3(左)所示,小预算下束搜索显著优于最佳N选1;但预算增大时,束搜索的改进大幅减弱,甚至低于最佳N选1基线。同一预算下,前瞻搜索通常表现更差,可能因模拟前瞻展开引入额外计算。搜索的收益递减可能源于PRM预测的过度利用。例如,部分案例(如图29)中,搜索导致模型在解末尾生成低信息的重复步骤;其他案例中,过度优化的搜索可能生成仅含1-2步的过短解。这解释了最强搜索方法(前瞻搜索)表现最差的原因。附录M列举了搜索发现的此类案例。
搜索改进的问题类型。为理解计算最优搜索策略,我们按难度分箱分析。比较束搜索(M=4)与最佳N选1。如图3(右),高生成预算下,束搜索与最佳N选1总体性能相近,但难度分箱分析揭示差异趋势:
- 易问题(难度1、2):更强的优化方法(束搜索)随预算增加性能下降,表明PRM信号被过度利用(类似过拟合)。
- 中等难度问题(难度3、4):束搜索持续优于最佳N选1。
- 最难问题(难度5):所有方法均无明显进展。
此发现符合直觉:易问题中,验证器对正确性的评估大多准确,束搜索进一步放大验证器学习的虚假特征,导致性能下降;难问题中,基础模型初始采样正确答案的概率低,搜索可引导模型更频繁生成正确答案。
计算最优搜索策略。上述结果表明,问题难度是预测最优搜索策略的有效统计量,且最优策略随难度显著变化。图4可视化"计算最优"扩展趋势:各难度等级下性能最优的搜索策略。可见,低生成预算下,无论使用真实难度(oracle)还是预测难度,计算最优策略均可用至多4倍更少的测试计算(如16代64)接近最佳N选1性能;高预算下,预测难度的部分收益减弱,但真实难度分箱仍显示最优扩展的持续改进。此结果证明,搜索时自适应分配测试计算可带来性能增益。
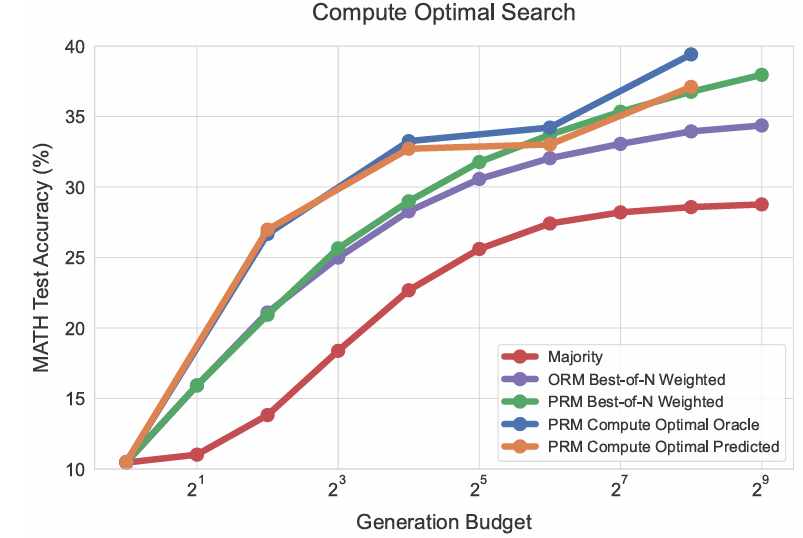
图4 | PRM搜索下计算最优测试计算分配与基线对比。通过按问题难度扩展测试计算,计算最优策略可用至多4倍更少的测试计算(如16代64)接近最佳N选1性能。"计算最优oracle"指基于真实正确性信息的难度分箱,"计算最优predicted"指基于PRM预测的难度分箱。两曲线基本重合。
验证器计算最优扩展的启示
验证器搜索方法的有效性高度依赖计算预算和问题难度。具体而言,束搜索在难问题和低预算下更有效,最佳N选1在易问题和高预算下更优。此外,通过按问题难度和测试计算预算选择最优搜索设置,计算最优策略可用至多4倍更少的测试计算接近最佳N选1性能。
6 优化提议分布
此前我们研究了基于验证器的搜索方法的测试时计算扩展特性。本节转向分析修改提议分布(第2节)的扩展特性。具体而言,我们使模型能够迭代修正自身答案,动态改进测试时的分布。直接提示现有LLMs修正自身错误对推理问题的性能提升效果有限[15]。因此,我们基于Qu等人[28]的方法,结合针对我们场景的修改,微调语言模型以迭代修正自身答案。首先描述如何训练和使用通过顺序关联先前尝试来优化提议分布的修正模型,随后分析修正模型在推理时的扩展特性。
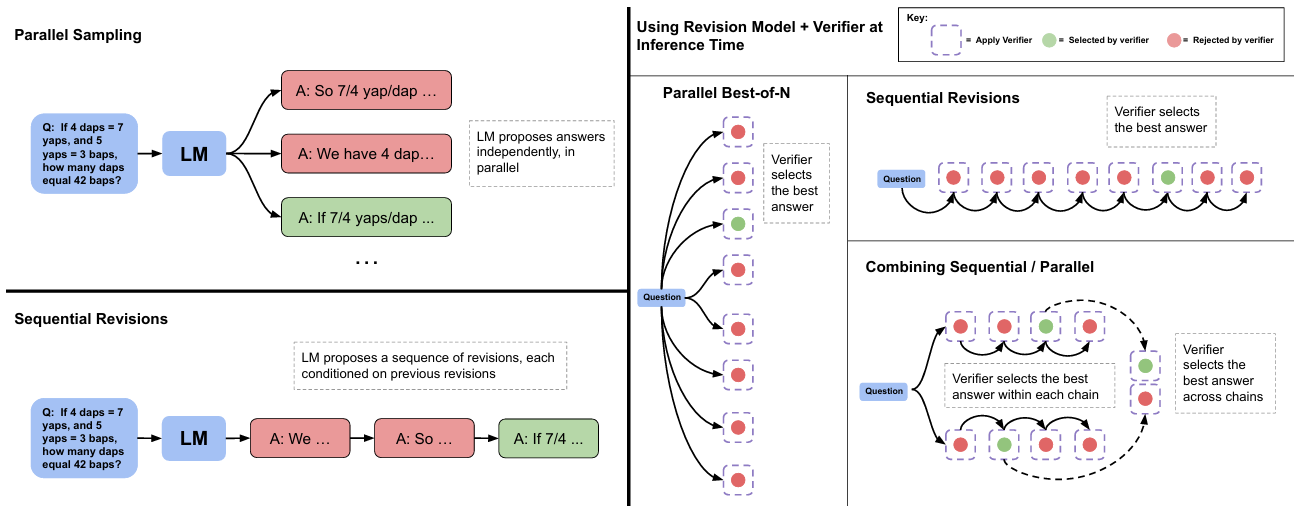
图5 | 并行采样(如最佳N选1)与顺序修正对比。左:并行采样独立生成N个答案;顺序修正逐个生成答案,每个答案基于前序尝试。右:在顺序和并行场景中,均可使用验证器选择最佳答案(如通过加权最佳N选1)。也可分配部分预算给并行采样,部分给顺序修正,实现两种策略的组合。此时先用验证器在每条顺序链内选最佳答案,再跨链选最优。
6.1 实验设置:训练与使用修正模型
我们的修正模型微调流程与[28]类似,但存在关键差异。微调需要包含错误答案序列后接正确答案的轨迹,以便通过监督学习(SFT)优化模型。理想情况下,正确答案应与上下文中的错误答案相关联,从而有效训练模型隐式识别上下文示例中的错误,并通过编辑修正错误,而非忽略上下文示例并从头重试。
生成修正数据。Qu等人[28]的多轮展开(multi-turn rollout)方法虽有效,但因计算成本问题在我们基础设施中不可行。因此,我们以较高温度并行采样64个响应,事后从中构建多轮展开轨迹。具体而言,遵循[1]的方法,将每个正确答案与该集合中的错误答案序列配对作为上下文,构建多轮微调数据。上下文中最多包含四个错误答案,具体数量从0到4的均匀分布中随机采样。我们使用字符编辑距离度量优先选择与最终正确答案相关的错误答案(见附录H)。虽然词元编辑距离并非完美的相关性度量,但该启发式方法足以关联上下文中的错误答案与正确目标答案,从而训练有意义的修正模型,而非随机配对无关联的响应。
推理时使用修正。给定微调后的修正模型,可在测试时从模型中采样一系列修正。尽管我们的修正模型仅训练过最多四个上下文答案,但可通过截断上下文至最近四个修正响应来采样更长链。图6(左)显示,随着修正链长度增加,模型在每一步的pass@1逐渐提升,表明模型能够有效学习利用上下文中的先前答案错误进行改进,甚至超越训练时的四步限制。
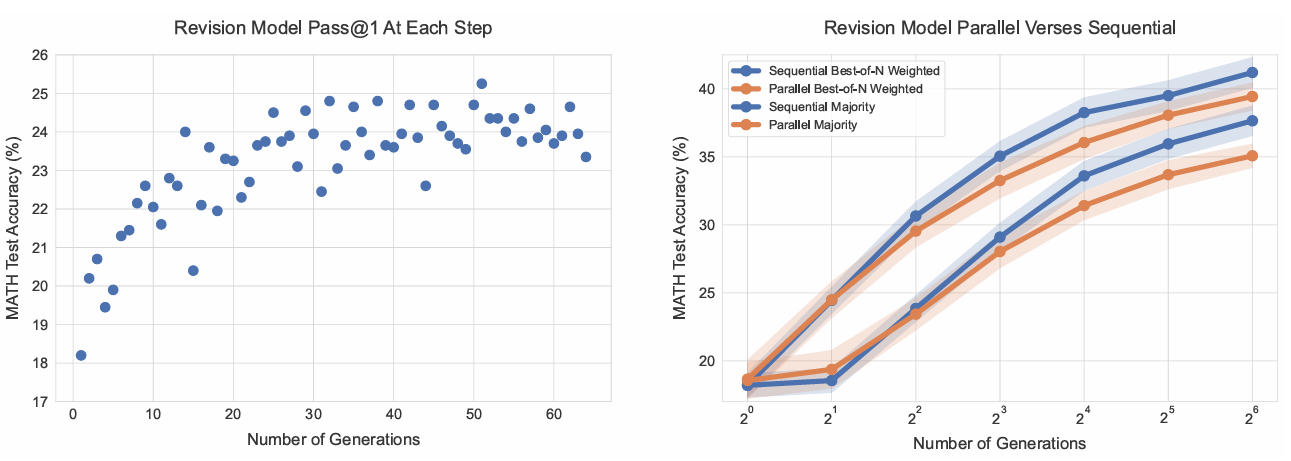
图6 | 左:修正模型在每一步的pass@1。经过每一步修正,pass@1逐渐提升,甚至超过训练时的四步限制。我们通过平均测试集每个问题的4条长度为64的修正轨迹的性能来估计每步pass@1。右:修正模型的顺序与并行采样对比。比较从修正模型并行生成N个初始答案与顺序生成N个修正的性能。当使用验证器或多数投票选择答案时,顺序生成略优于并行生成。
需注意,推理时存在分布偏移:模型仅在上下文包含错误答案的情况下训练,但测试时上下文可能包含正确答案。此时,模型可能在下一步修正中将正确答案转为错误答案。类似Qu等人[28],我们发现约38%的正确答案通过朴素方法被修正模型转为错误答案。因此,我们采用顺序多数投票或基于验证器的选择机制,从模型生成的修正序列中选出最正确的答案(见图5),以生成最终答案。
对比实验。为测试通过修正优化提议分布的有效性,我们公平比较顺序采样N个修正与并行采样N个问题尝试的性能。图6(右)显示,无论使用基于验证器还是多数投票的选择机制,顺序采样均略优于并行采样。
6.2 分析结果:修正的测试时扩展
此前观察到顺序采样优于并行采样,但两者特性可能不同。并行采样更似全局搜索,可能覆盖多种完全不同的解题方法(如不同候选采用不同高层策略)。顺序采样则更似局部优化,修正已部分正确的响应。由于两者互补,应通过分配部分推理预算给并行采样(如N\sqrt{N}N )、部分给顺序修正(如N\sqrt{N}N )来平衡。下文将展示顺序与并行采样的计算最优比率存在性,并基于问题难度分析其优劣。
顺序与并行计算的权衡。为理解如何最优分配顺序与并行计算,我们扫描不同比率。图7(左)显示,在固定生成预算下,存在使准确率最大的理想顺序-并行比率。图7(右)进一步按难度分箱分析,使用验证器选择时,简单问题在全顺序计算下表现最佳,而困难问题需平衡顺序与并行计算。
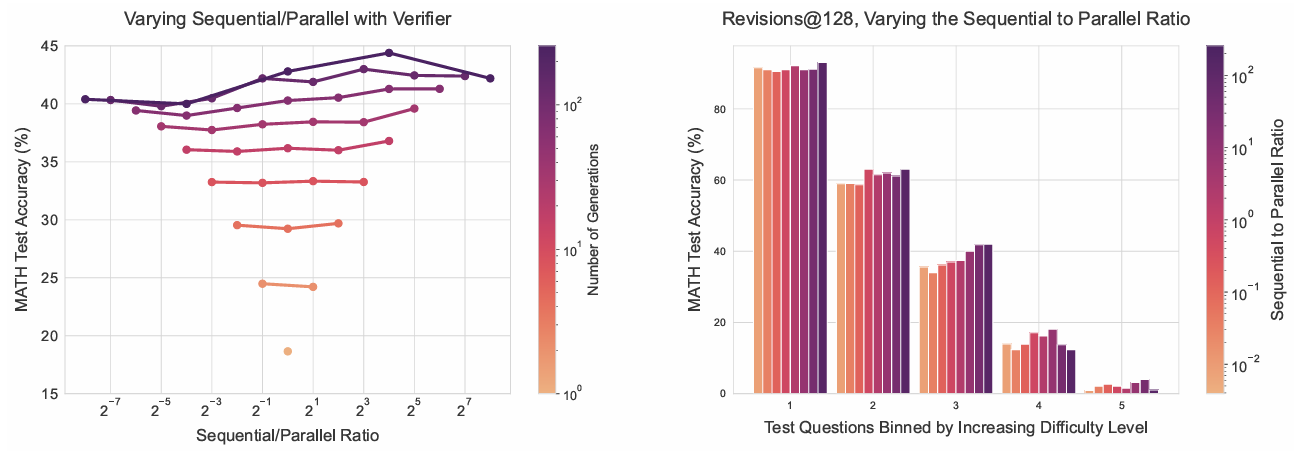
图7 | 左:变化顺序修正与并行采样的预算分配比率。每条线代表固定生成预算下比率变化的表现,使用验证器选择答案。可见增加顺序修正倾向优于更多并行计算,但高预算下存在平衡两者比率的理想点。右:生成预算128下按难度分箱的变化顺序-并行比率表现。使用验证器选择时,简单问题在全顺序计算下最佳,困难问题需平衡顺序与并行计算。
计算最优修正策略。鉴于顺序与并行采样的有效性依赖问题难度,可按难度分箱选择理想比率。图8展示使用真实难度(oracle)与预测难度时,计算最优策略的结果。两种情况下,通过修正优化提议分布均可显著提升测试时计算扩展效率。高生成预算下,并行采样性能趋于平稳,而计算最优策略持续改进。无论真实还是预测难度,计算最优策略均可用至多4倍更少测试计算(如64样本代256)超越最佳N选1基线。总体表明,通过按提示调整提议分布,可更高效扩展测试时计算。
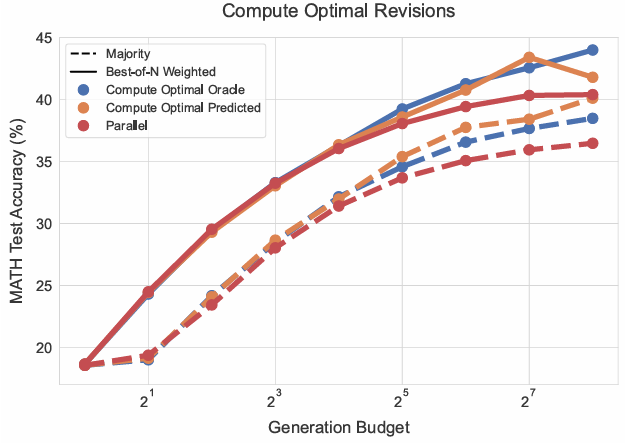
图8 | 计算最优测试时计算分配与修正模型并行基线对比。通过按问题难度最优扩展测试计算,计算最优策略可用至多4倍更少测试计算(如64样本代256)超越最佳N选1。"计算最优oracle"指基于真实正确性信息的难度分箱,"计算最优predicted"指基于PRM预测的难度分箱。
修正提议分布的计算最优扩展启示
顺序(如修正)与并行(如最佳N选1)测试时计算存在权衡,理想比率依赖计算预算和问题难度。简单问题更适合全顺序计算,困难问题需平衡顺序与并行计算。通过按问题难度和测试计算预算选择最优设置,计算最优策略可用至多4倍更少测试计算超越并行最佳N选1基线。
7 综合分析:交换预训练与测试时计算
此前我们看到,额外测试时计算可通过优化提议分布或搜索验证器,使模型表示比基础LLM更复杂的分布,从而提升性能。现假设:这种表示复杂分布的灵活性是否意味着测试时计算可替代更高容量模型或更多预训练FLOPs?本节研究此问题的程度。我们提出以下问题:
问题:交换预训练与测试时计算
假设模型预训练消耗XXX FLOPs,计划推理消耗YYY FLOPs。若需通过增加总FLOPs预算至M(X+Y)M(X+Y)M(X+Y)(即预训练和推理总FLOPs为M(X+Y)M(X+Y)M(X+Y))来提升性能,应将FLOPs用于增加预训练计算还是额外测试时计算?
增加预训练FLOPs需决定是扩展数据还是参数[14]。我们聚焦参数扩展且训练数据量固定的设置(类似开源LLaMA系列[41]),此为典型预训练扩展方式,暂不分析数据与参数均衡扩展的预训练计算最优扩展[29],留待未来工作。
定义FLOPs交换率 。预训练FLOPs近似为X=6NDpretrainX=6ND_{\text{pretrain}}X=6NDpretrain[14],推理FLOPs为Y=2NDinferenceY=2ND_{\text{inference}}Y=2NDinference[29],其中NNN为模型参数量,DpretrainD_{\text{pretrain}}Dpretrain为预训练词元数,DinferenceD_{\text{inference}}Dinference为推理生成词元数。若参数扩展MMM倍,预训练和推理FLOPs(因更大模型的贪心解码成本)均增加MMM倍(总FLOPs为M(X+Y)M(X+Y)M(X+Y))。
为用小模型的测试时计算匹配大模型的FLOPs,需将小模型推理计算扩展M+3(DpretrainDinference)(M−1)\begin{array}{r}M+3\left(\frac{D_{\text{pretrain}}}{D_{\text{inference}}}\right)(M-1)\end{array}M+3(DinferenceDpretrain)(M−1)倍。测试时计算可扩展量依赖比率DpretrainDinference\frac{D_{\text{pretrain}}}{D_{\text{inference}}}DinferenceDpretrain,其倒数记为R=DinferenceDpretrainR=\frac{D_{\text{inference}}}{D_{\text{pretrain}}}R=DpretrainDinference。不同场景下RRR差异显著:大规模生产场景中,推理词元数可能远超预训练(R≫1R \gg 1R≫1);而自我改进场景中,测试时计算用于优化模型,推理词元数可能远少于预训练(R≪1R \ll 1R≪1)。
测试时与预训练计算对比
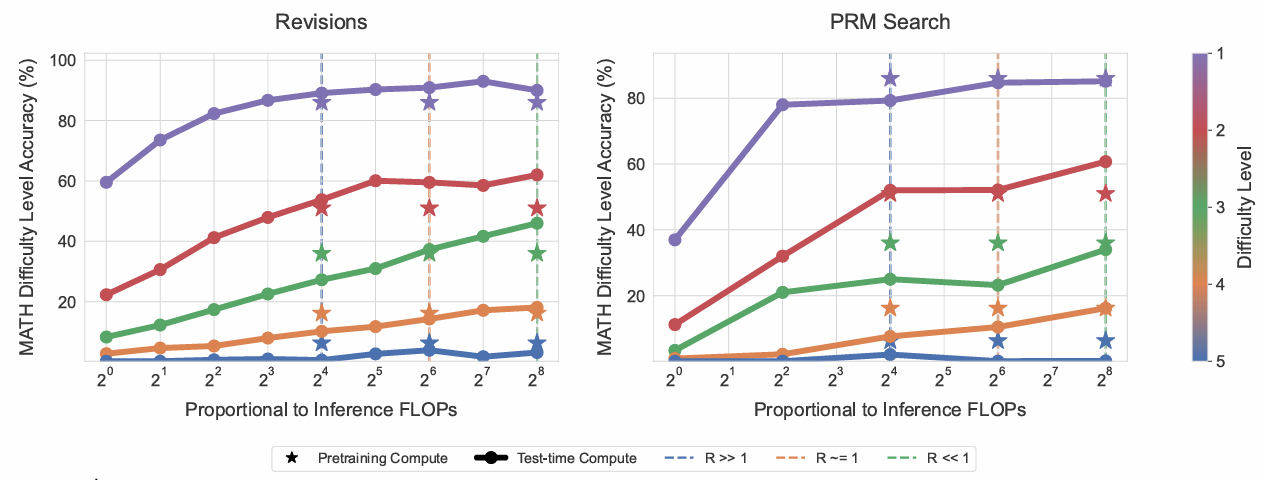
图9 | FLOPs匹配评估中预训练与测试时计算的权衡。每条线代表计算最优策略在各真实难度分箱下的性能,左为修正,右为搜索。星标表示约14倍参数的大模型贪心解码性能。x轴为测试时计算预算,星标位置对应三种推理负载(即R=\\frac{D_{\\text{inference}}}{D_{\\text{pretrain}}})下扩展参数与测试时计算的FLOPs等价点。若星标在线下方,表示测试时计算更有效;若在上方,则预训练更有效。可见,简单问题或低推理负载(R \\ll 1)时,测试时计算通常优于参数扩展;困难问题或高推理负载(R \\gg 1)时,预训练更有效。
图9中,我们比较计算最优策略与14倍参数大模型在三种RRR值(0.16[R≪1R \ll 1R≪1], 0.79[R∼1R \sim 1R∼1], 22[R≫1R \gg 1R≫1])下的表现。若仅遇困难问题(难度4/5)或RRR较大(高推理负载),预训练通常更有效(星标在线上方);若主要为简单或中等难度问题(难度1/2/3,有时4)或RRR较小(低推理负载,如自我改进管道),测试时计算更优。
交换预训练与测试时计算的启示
测试时与预训练计算并非1:1可交换。简单/中等难度问题(模型能力范围内)或低推理负载场景下,测试时计算可轻易替代额外预训练;困难问题(超出基础模型能力)或高推理负载场景下,预训练更有效。
8 讨论与未来工作
本研究系统分析了通过搜索验证器或优化提议分布来扩展测试时计算的有效性,重点关注数学推理。发现方法有效性高度依赖问题难度(从基础模型能力视角)。由此引入"计算最优"测试时计算扩展概念,即根据提示动态调整策略以在给定预算下提升性能。采用此策略可使测试时计算扩展效率提升2−42-42−4倍。在FLOPs匹配场景中,首次证明简单方法(如修正和搜索)的测试时计算在特定提示下可超越预训练FLOPs投入。但研究仍存局限,未来工作可从以下方面改进:
进一步优化测试时计算扩展。本研究聚焦验证器和提议分布(通过修正)的扩展,虽在修正中结合验证器(第6节),但未尝试PRM树搜索与修正的组合,也未研究如批判-修正[23]等其他技术。未来工作应探索多种方法的组合以提升测试时计算扩展。此外,当前方法在困难问题上的增益有限,需开发新策略突破此限制。
快速评估问题难度。我们使用问题难度作为计算最优策略的充分统计量,虽有效但评估难度需额外测试时计算。未来工作可探索更高效的难度估计方法(如预训练或微调模型直接预测问题难度),或动态切换难度评估与解题。
测试时与训练时计算的交织。本研究仅关注测试时计算扩展及其与预训练的权衡,但未来可设想将额外测试时计算的输出蒸馏回基础LLM,构建开放域自然语言的自改进循环。为此,需扩展当前发现,研究测试时计算的输出如何用于改进基础模型。
附录
A. 相关研究
语言模型推理。近年来,语言模型在挑战性数学推理任务上的性能迅速提升[20,22,25,32,39]。这些改进可归因于四个主要因素:1)在大量数学相关语料库上持续预训练[20,22,32,39];2)通过针对特定推理任务的强化学习微调[32,35,49,50]或使模型能够迭代批判并修正自身答案[4,8,23,30],从而优化LLM的提议分布;3)通过微调验证器[6,7,10,22,40,42,45,48]使LLM受益于额外测试时计算。本研究基于第二和第三类研究,分析测试时计算扩展在以下两方面的优化程度:1)优化LLM的提议分布;2)基于验证器进行搜索。
分析测试时计算扩展。Jones[16]此前研究了蒙特卡洛树搜索在棋盘游戏Hex中训练时与测试时计算的权衡。我们则聚焦于全尺度语言模型数学推理问题的分析。Villalobos和Atkinson[44]的综述分析了多领域的训练与推理计算权衡,但其语言模型分析多集中于已知真实答案的场景。相比之下,我们关注真实答案未知的场景。此外,强化学习领域已提出MCTS[19]等方法,旨在平衡测试时与训练时计算以实现迭代自博弈。本研究成果可助力开发适用于开放域自然语言的类似算法。
通过测试时计算增强LLM。除验证器和修正外,多项研究提出了使LM利用测试时计算进行推理的替代方法。例如,Wang等人[46]通过分层假设搜索实现归纳推理能力。相关研究还提出在测试时为语言模型配备工具[11,26,27],显著提升下游任务性能。最后,若干研究提出了无监督学习思维token的方法[12,51],使模型更有效利用采样更长序列带来的额外测试时计算。本研究聚焦测试时计算扩展的两种主要机制(验证器与修正),但分析方法(如基于问题难度的计算最优扩展)原则上可应用于其他测试时计算扩展方法,我们认为这是未来研究的有趣方向。
B. 额外修正结果
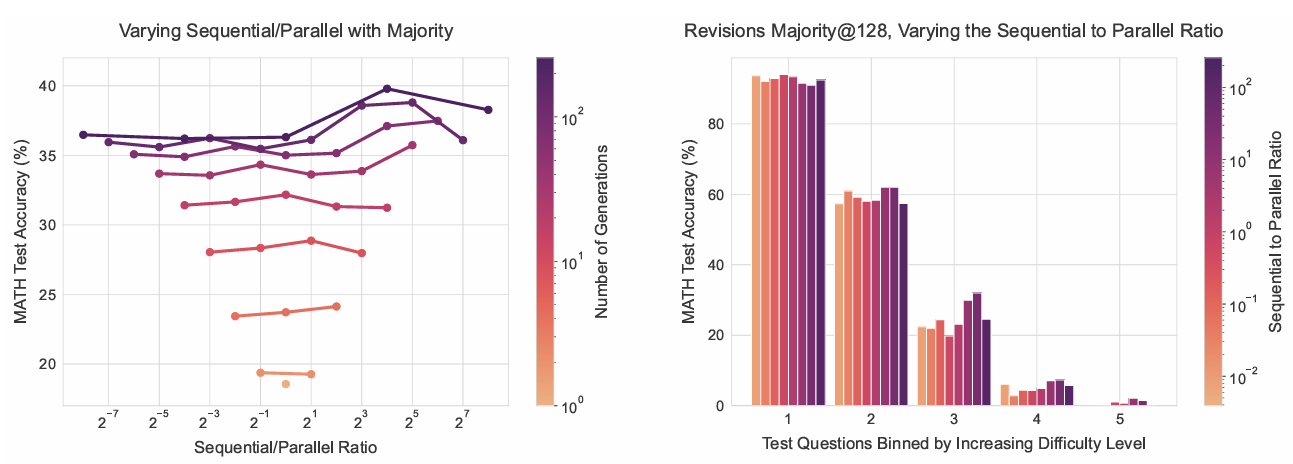
图10展示了使用PaLM 2-S*修正模型进行多数选择的结果。多数选择下,趋势与图7中验证器选择的结果类似。
C. 无监督难度分箱
我们通过平均2048个样本的PRM最终答案评分来计算无真实答案的难度分箱,从而获得对应问题的价值估计。随后将测试集每个问题的价值估计分为五等分(采用与真实难度分箱相同的流程),称为"预测难度"而非"真实难度"。此流程成本极高,因需生成大量样本。尽管分析中未计入此成本,但实际生产场景中可能存在问题。更高效的方法是微调模型直接预测问题正确性,本研究未探索此方向,留待未来研究更廉价的难度估计方法。
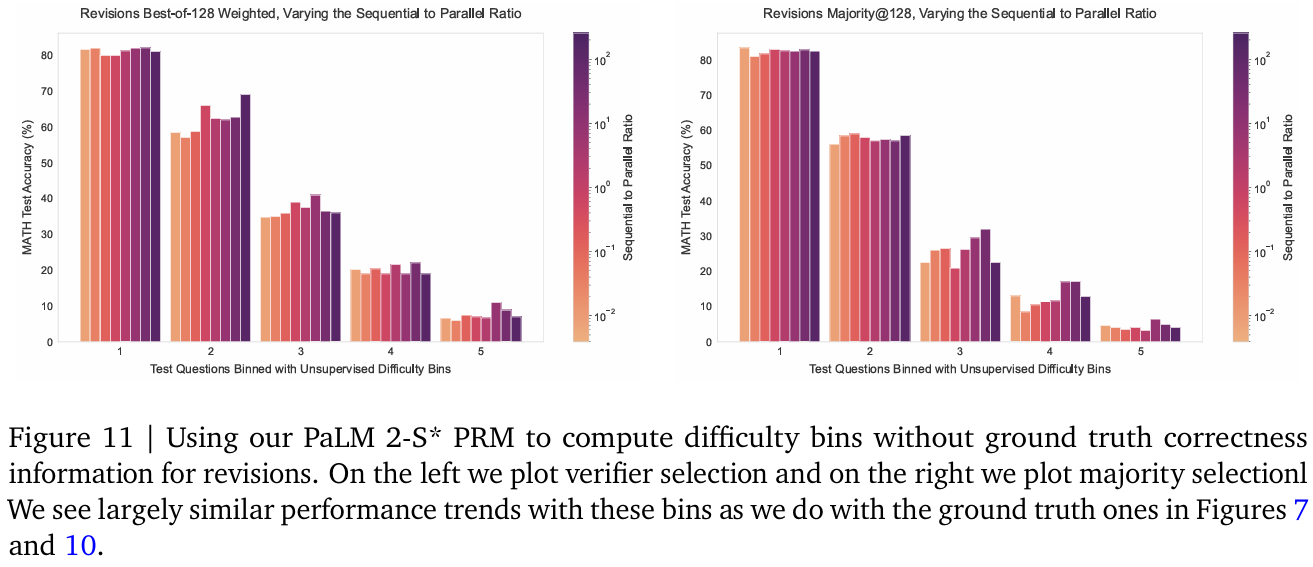
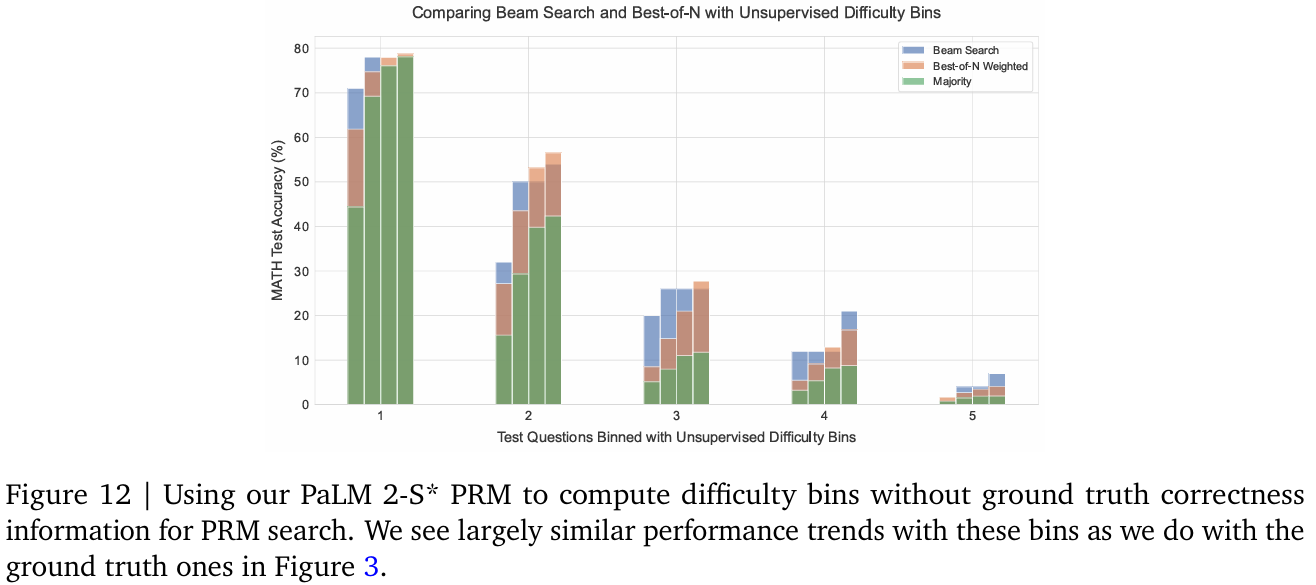
图12和图11分别展示了使用预测难度分箱的PRM搜索与修正结果。两种设置下,预测难度分箱均呈现与真实难度分箱类似的趋势。
D. PRM训练细节
我们将PRM微调为二分类器,预测解决方案每一步的0-1值。模型通过蒙特卡洛展开获得的软标签训练,使用二分类交叉熵损失函数(例如−(ylog(y^)+(1−y)log(1−y^))-(y\log(\hat{y})+(1-y)\log(1-\hat{y}))−(ylog(y^)+(1−y)log(1−y^))),其中yyy为软真实值,y^\hat{y}y^为模型预测值。使用AdamW优化器微调基础模型,参数为:学习率3e−53\mathrm{e-}53e−5,批大小128,丢弃率0.05,Adam参数(0.9,0.95)(0.9,0.95)(0.9,0.95)。通过早停选择验证损失最低的 checkpoint,验证集为PRM80Ok训练集的10%随机样本。
PRM在每个问题的少样本提示基础模型上微调,每问题采样16个样本。每步使用16次蒙特卡洛展开(基于相同基础模型和提示)估计步级价值。过滤掉所有无法输出有效可解析最终答案的样本,因初始实验发现此类样本损害PRM性能。
图11和图12分别展示了使用PaLM 2-S* PRM计算无真实答案难度分箱的修正与PRM搜索结果,趋势与真实难度分箱(图7和图3)一致。
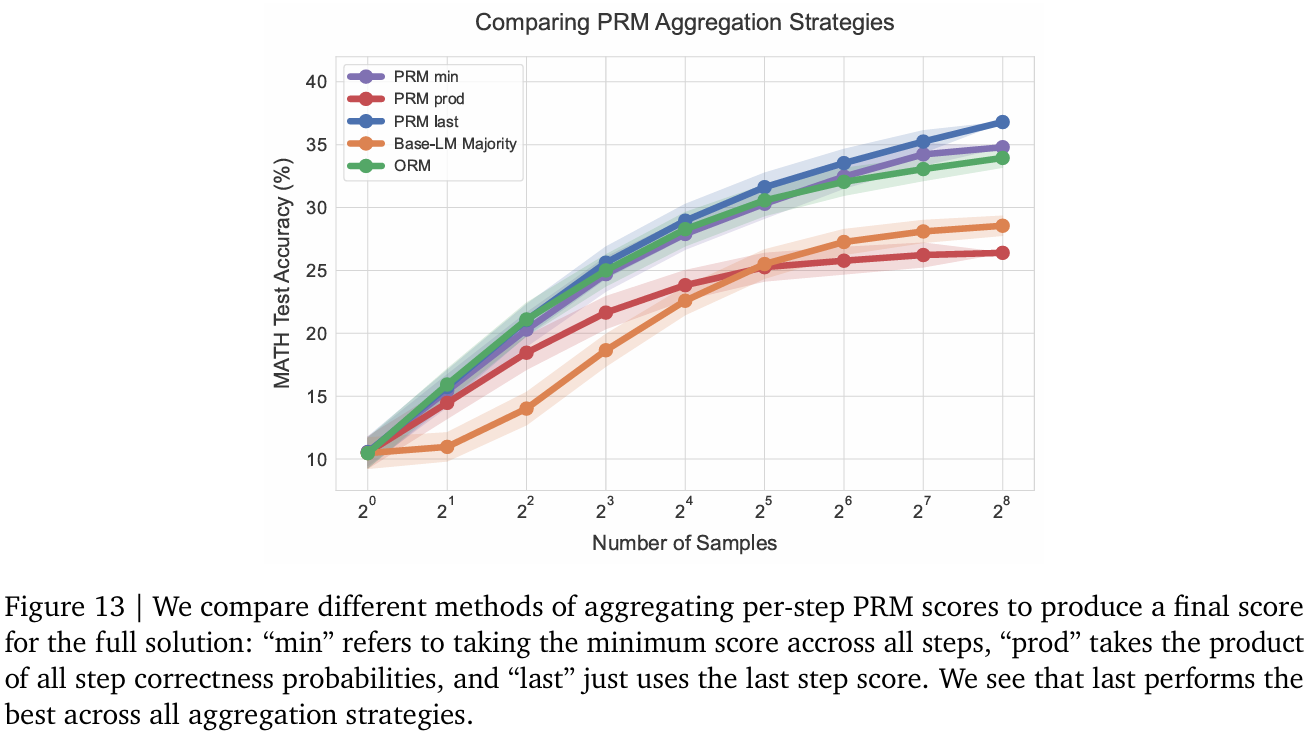
E. PRM聚合策略对比
我们对比了不同聚合步级PRM评分以生成最终解决方案评分的方法:1)取所有步的最小分(Lightman等人[22]方法,即"min");2)取所有步正确概率的乘积(即"prod");3)仅取最后一步预测(即"last")。图13显示,最后一步预测在所有聚合策略中表现最佳。此前研究[22,45]发现"min"最优,但我们认为差异源于我们的验证器基于软蒙特卡洛回报标签训练,与二进制正确性标签表面差异显著,故其他聚合策略效果不同。
有趣的是,使用最后一步聚合时,PRM实质上被用作ORM。但PRM性能优于ORM,表明我们的步级PRM训练更多是表征学习,而非纯推理工具。未来研究应进一步探索此方向。
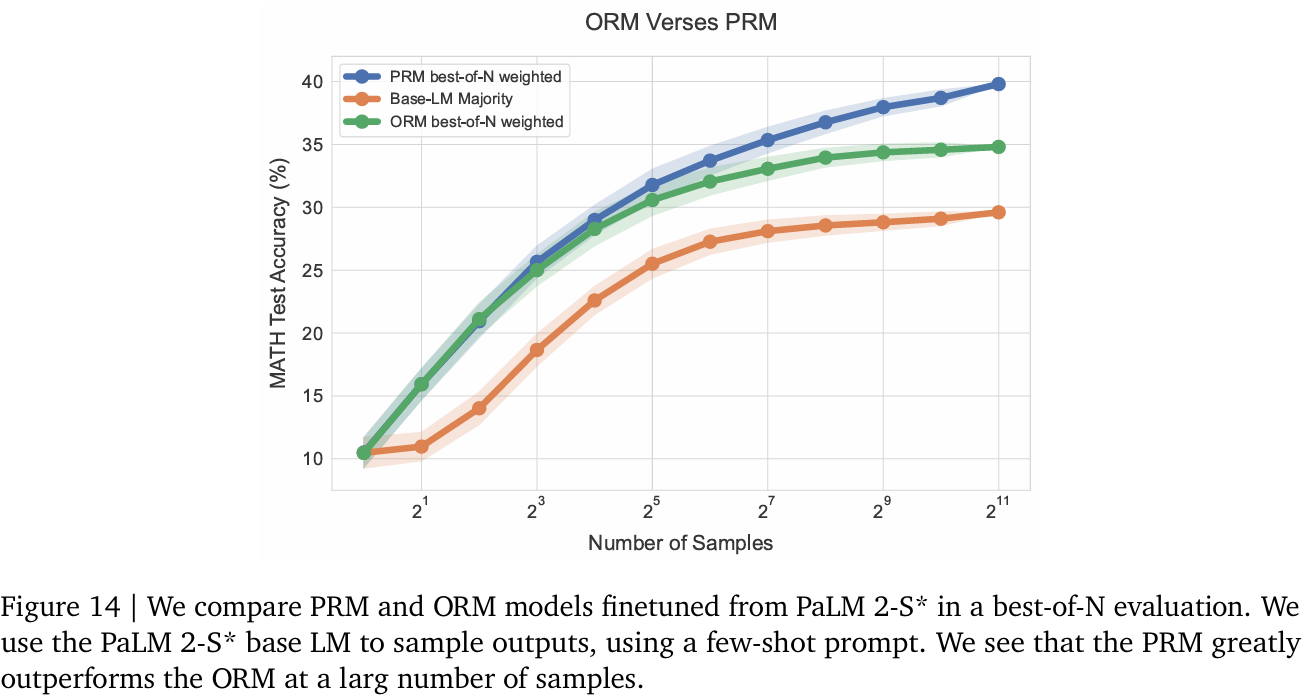
F. PRM与ORM对比
我们使用PaLM 2-S*基础LM训练了PRM和ORM模型。图14显示,PRM性能显著优于ORM,且差距随样本量增加而扩大。PRM使用最后一步预测评分答案(如附录E所述)。
G. 提示细节
为使基础模型输出可应用PRM的逐步格式答案,我们采用4样本提示,样本选自Lightman等人[22]发布的PRM800k数据。具体使用第1阶段训练集的GPT-4生成正确答案示例,包含正确逐步格式。初始实验发现此提示与Lewkowycz等人[20]的提示效果相似。该提示用于生成PRM和修正模型的训练数据,也在测试集上用于PRM搜索。最终答案评分采用Lightman等人[22]发布的评分函数。
H. 修正模型微调细节
修正模型的微调流程遵循第6.1节所述方法。我们首先为每个问题采样64个输出,并过滤掉所有以无效解结尾的答案。对于每个正确答案,我们统一随机采样0到4之间的整数,指示在训练轨迹中包含多少个错误答案作为上下文。正确答案作为轨迹的最后一个答案(模型被训练生成该答案),错误答案被包含在上下文中。若采样数大于0,我们根据字符级编辑距离指标选择最接近的错误答案作为轨迹的最后一个错误答案,目标是选择与正确答案有一定关联的错误答案以提升学习效果。剩余错误答案从可用答案中随机采样。若采样到的错误答案不足4个,我们将均匀分布的最大值调整为实际错误样本数。我们使用此流程为训练集中的所有问题生成轨迹,并基于这些轨迹中的正确答案微调基础语言模型。优化器采用AdamW,参数为:学习率1e−51\mathrm{e}{-5}1e−5,批大小128,丢弃率0.0,Adam参数(0.9,0.95)(0.9,0.95)(0.9,0.95)。
我们发现,基于上述流程生成的验证集评估损失并不适合作为早停信号。实际上,在验证损失开始上升后的检查点往往具备更强的修正能力。这可能是因为微调后的修正模型生成的轨迹属于策略外数据,自然与模型自身策略内生成的轨迹分布不同。因此,我们选择在验证集过拟合后稍晚的检查点作为修正模型。
I. 修正模型选择准则
如第6.1节所述,为有效使用修正模型,需部署两类选择标准:1)ORM验证器;2)多数投票。
对于ORM验证器,我们根据附录J的流程在修正模型输出上训练ORM。推理时,使用该验证器选择最佳答案。由于存在两类聚合维度(修正轨迹内部和轨迹之间),我们采用分层策略:首先在每条修正轨迹内通过最佳N加权聚合选择最高分答案,然后在所有轨迹的选中答案中再次进行最佳N加权聚合,最终输出作为最终预测。
对于多数投票,我们发现分层聚合在轨迹数或长度较小时存在问题(样本不足导致多数投票失效)。因此,多数投票直接聚合所有轨迹的所有答案,取多数作为最终答案。此方法在扩展性上表现更稳定。
J. 修正模型验证器训练
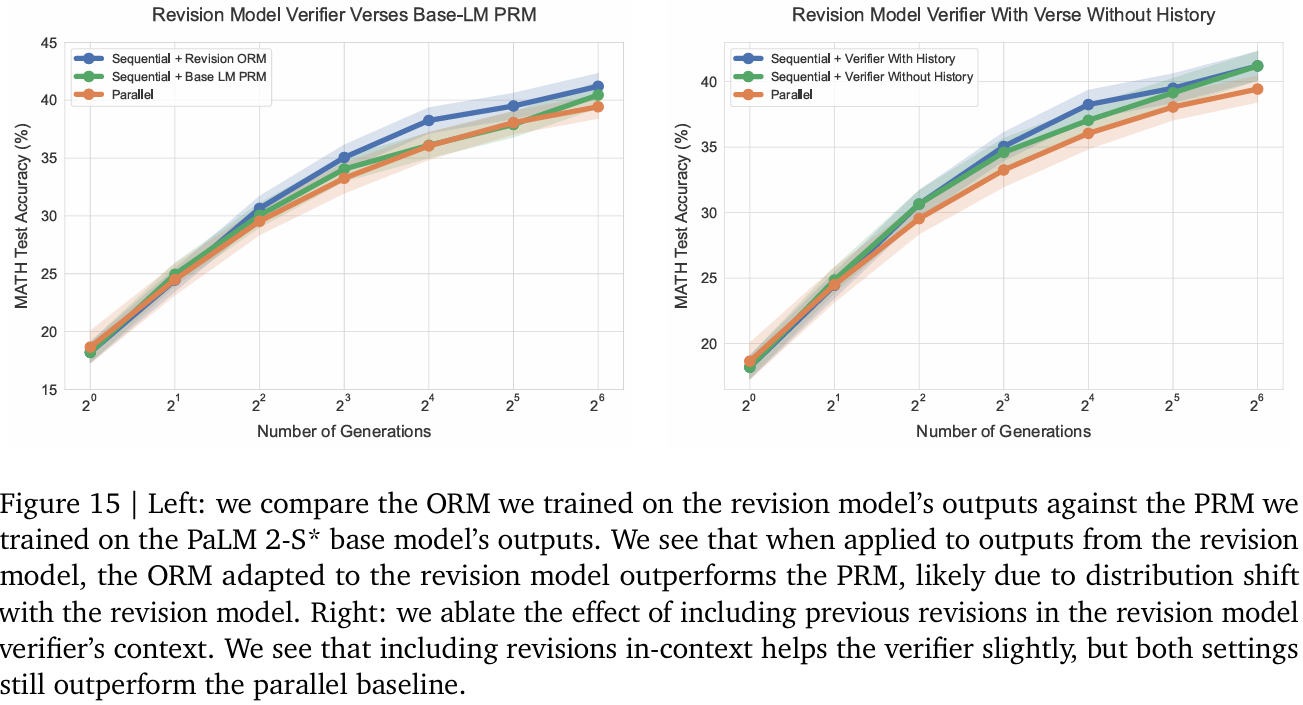
我们发现,在PaLM 2-S修正模型输出上训练的PRM效果不佳(见图15(a)),可能是由于修正模型导致的分布偏移。因此,我们为PaLM 2-S修正模型单独训练ORM验证器(未选择PRM因生成步级标签成本过高)。
针对修正场景,我们略微调整标准ORM:在微调时将历史修正步骤作为上下文输入,使验证器与修正模型共享相同上下文,从而在评分时能参考历史尝试。其余实验细节与PRM训练一致。
实证表明,包含历史修正的上下文能略微提升验证器性能(见图15(b))。即使不包含历史修正,顺序修正仍略优于并行采样,说明顺序采样的提升不仅源于验证器上下文。
K. ReST EM修正模型实验
我们尝试用简化RL算法ReST EM[35]进一步优化PaLM 2-S*修正模型。具体而言,在MATH训练集上为每个问题生成最多5步的64条修正轨迹,并在轨迹中首次出现正确答案时停止。基于此数据微调基础LM。为帮助模型学习任务,我们显式平衡了轨迹长度的分布。
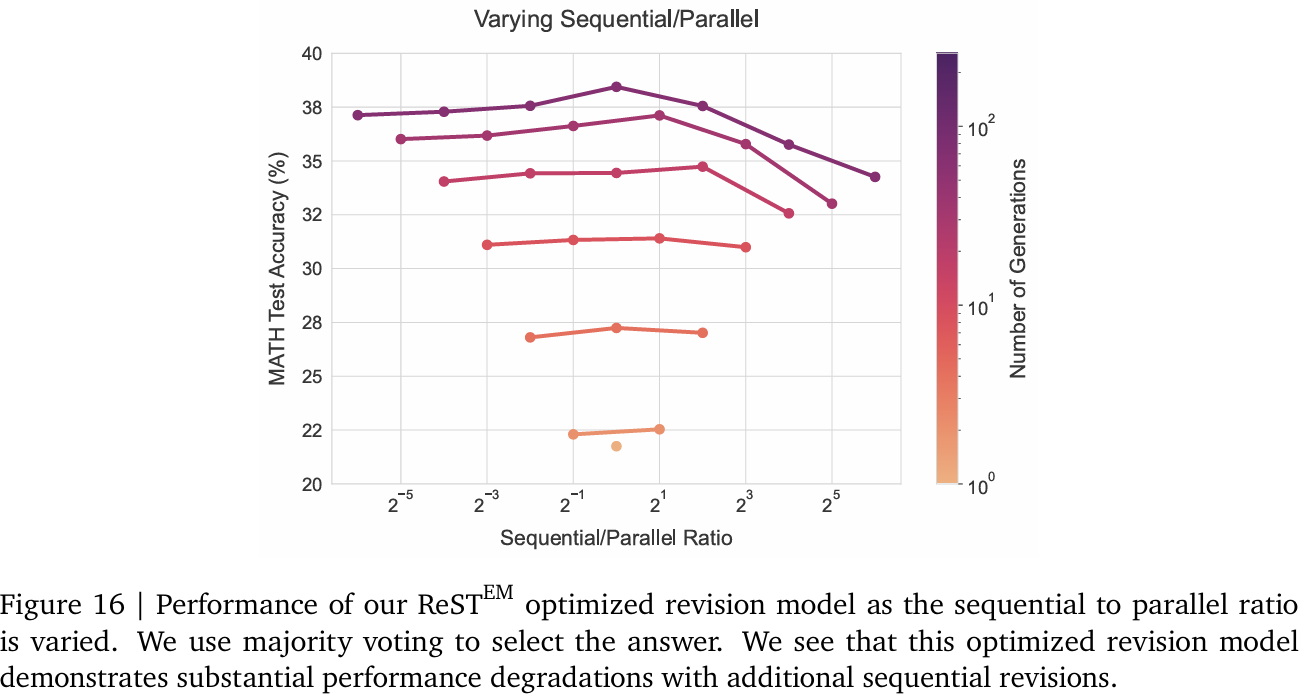
图16展示了新修正模型随顺次-并行比例变化的性能。可见,额外顺次修正对此模型性能损害显著。我们推测,因ReST EM在线数据采集加剧了修正数据中的虚假关联,导致优化后的模型无法有效学习修正任务。我们认为,采用Qu等人[28]的离线数据收集策略可能更有效,留待未来研究。
L. 修正模型输出示例
图17-23展示了修正模型的多个输出示例。







M. PRM束搜索输出示例
图24-29展示了PRM束搜索的多个输出示例,包含每步的PRM评分(0到1之间)。


