🍋🍋AI学习🍋🍋
🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。
💖如果觉得博主的文章还不错的话,请点赞👍+收藏⭐️+留言📝支持一下博主哦🤞
网络非线性因素理解
没有引入非线性因素的网络等价于使用一个线性模型来拟合
通过给网络输出增加激活函数, 实现引入非线性因素, 使得网络模型可以逼近任意函数, 提升网络对复杂问题的拟合能力
激活函数 用于对每层的输出数据进行变换 , 进而为整个网络注入了非线性因素 。此时, 神经网络就可以拟合各种曲线。如果不使用激活函数,整个网络虽然看起来复杂,其本质还相当于一种线性模型。
常见激活函数
激活函数主要用来向神经网络中加入非线性因素,以解决线性模型表达能力不足的问题,它对神经网络有着极其重要的作用。我们的网络参数在更新时,使用的反向传播算法(BP),这就要求我们的激活函数必须可微。
Sigmoid 激活函数
激活函数公式:
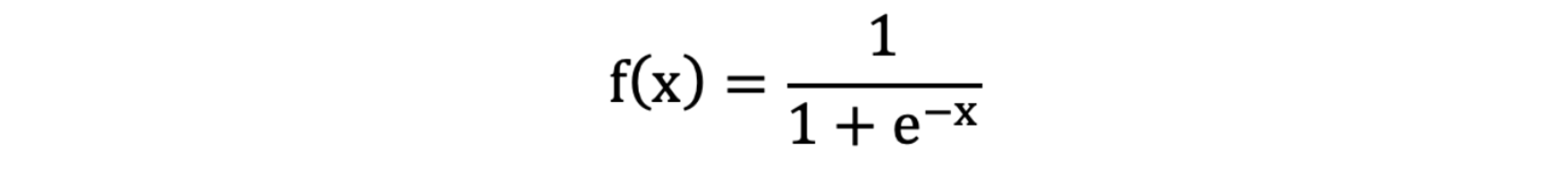
激活函数求导公式:
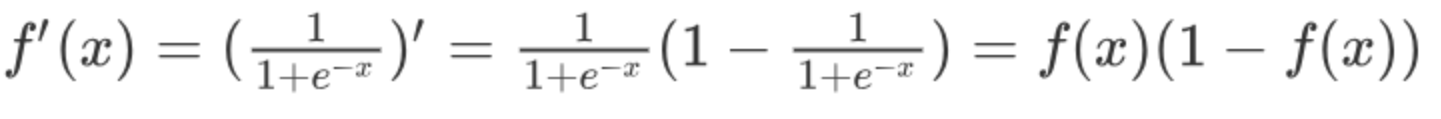
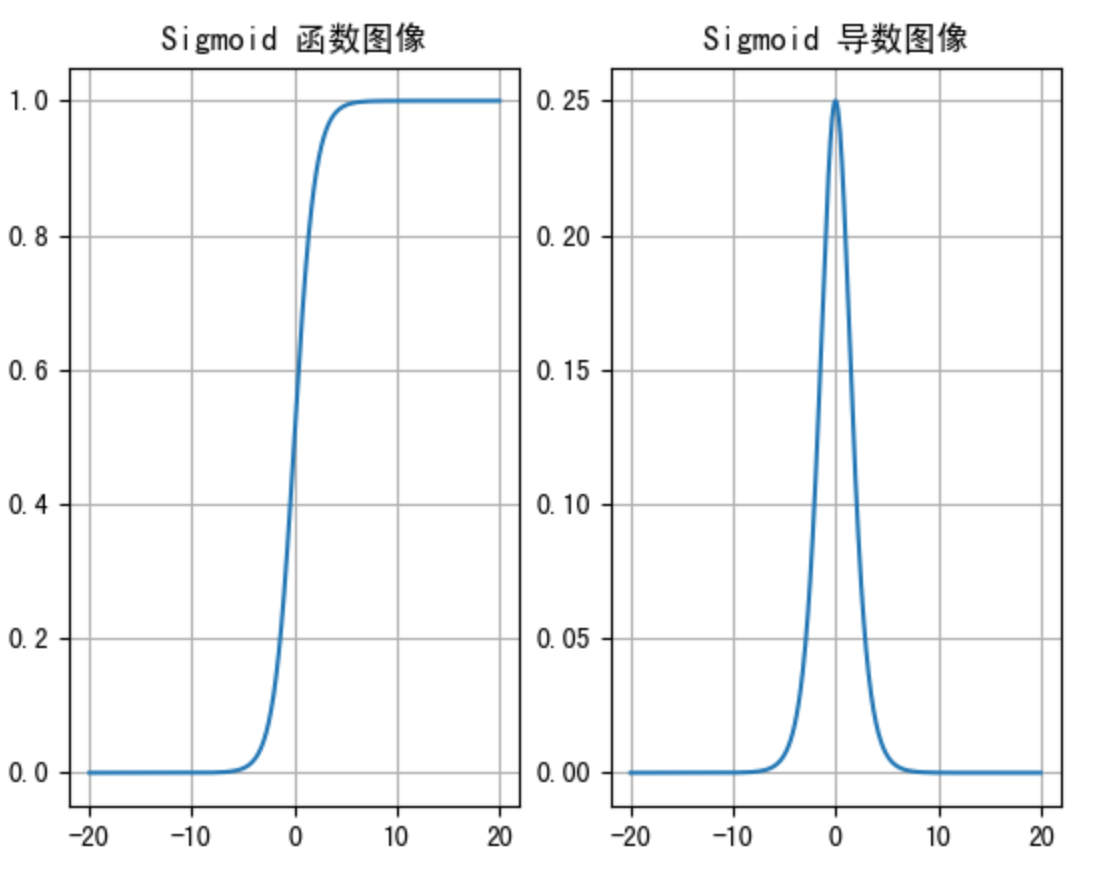
sigmoid 激活函数的函数图像如下:
-
从sigmoid函数图像可以得到,sigmoid 函数可以将任意的输入 映射到 (0, 1) 之间,当输入的值大致在**<-6或者>6**时,意味着输入任何值得到的激活值都是差不多的,这样会丢失部分的信息。比如:输入100和输入10000经过 sigmoid的激活值几乎都是等于1的,但是输入的数据之间相差100倍的信息就丢失了。
-
对于sigmoid函数而言,输入值在**[-6, 6]** 之间输出值才会有明显差异 ,输入值在**[-3, 3]** 之间才会有比较好的效果
-
通过上述导数图像,我们发现导数数值范围是 (0, 0.25) ,当输入的值**<-6或者>6** 时,sigmoid激活函数图像的导数接近为 0 ,此时网络参数将更新极其缓慢,或者无法更新。
-
一般来说,sigmoid网络在5层之内 就会产生梯度消失 现象。而且,该激活函数的激活值并不是以0为中心的,激活值总是偏向正数,导致梯度更新时,只会对某些特征产生相同方向的影响,所以在实践中这种激活函数使用的很少。sigmoid函数一般只用于二分类的输出层。
Tanh 激活函数
Tanh叫做双曲正切函数,其公式如下:
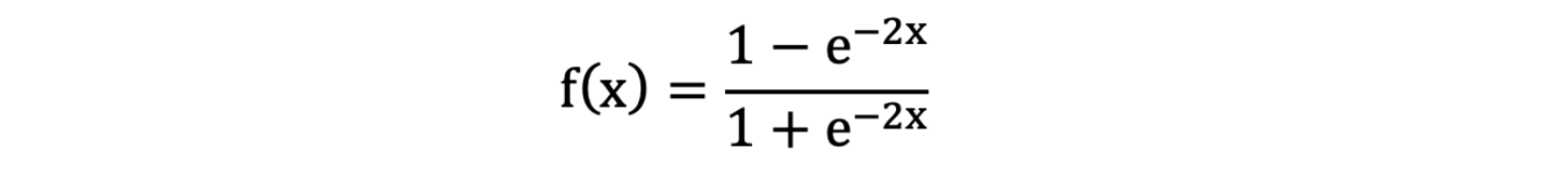
激活函数求导公式:
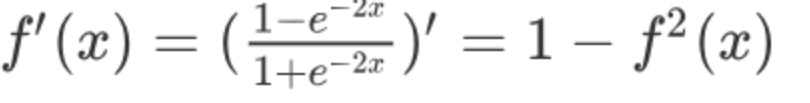
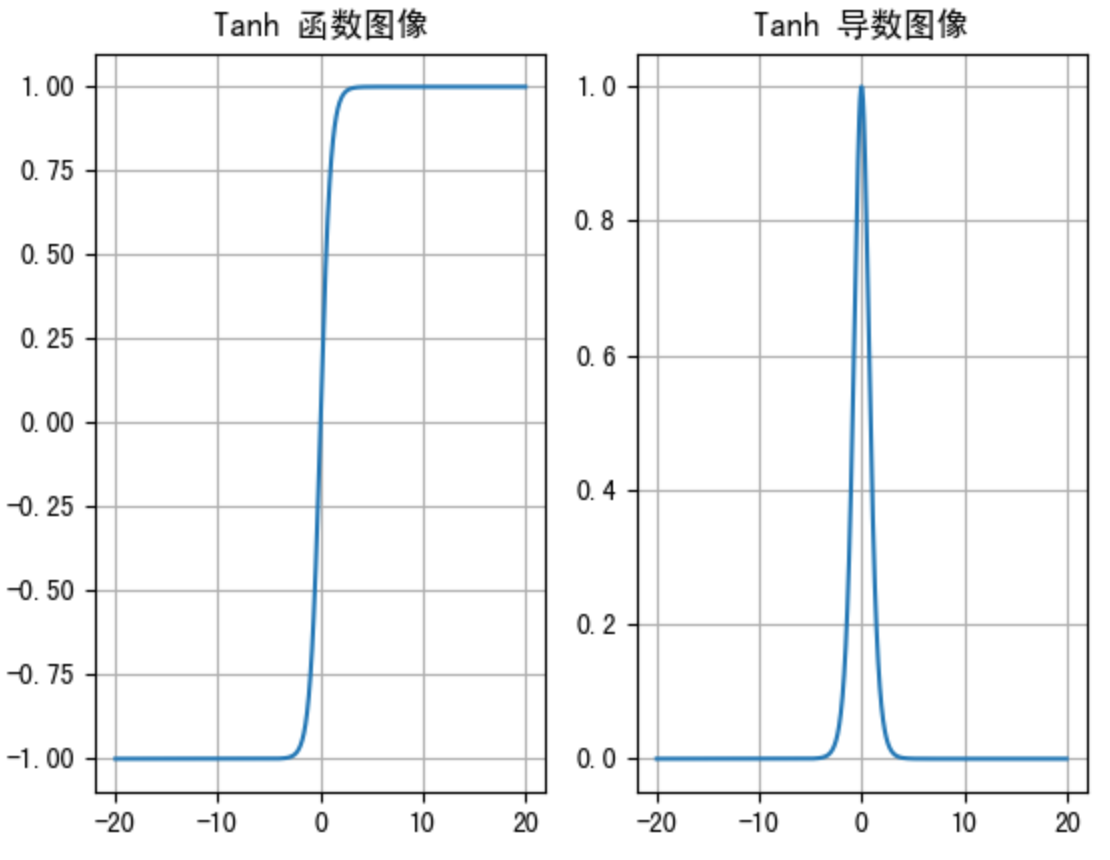
Tanh的函数图像、导数图像如下:
-
由上面的函数图像可以看到,Tanh函数将输入映射到(-1, 1)之间 ,图像以0为中心,激活值在0点对称,当输入的值大概**<-3或者>3** 时将被映射为-1或者1。其导数值范围 (0, 1) ,当输入的值大概**<-3或者>3**时,其导数近似0。
-
与Sigmoid相比,它是以0为中心的,使得其收敛速度要比Sigmoid快,减少迭代次数。然而,从图中可以看出,Tanh两侧的导数也为0,同样会造成梯度消失。
-
若使用时可在隐藏层使用tanh函数 ,在输出层使用sigmoid函数。
ReLU 激活函数
ReLU 激活函数公式如下:
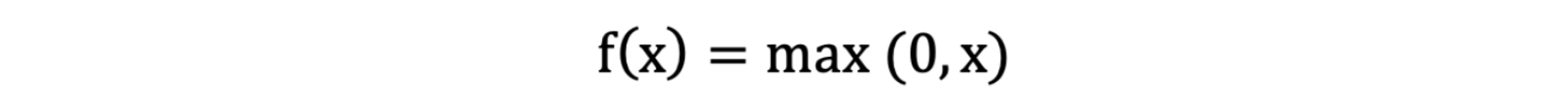
激活函数求导公式:
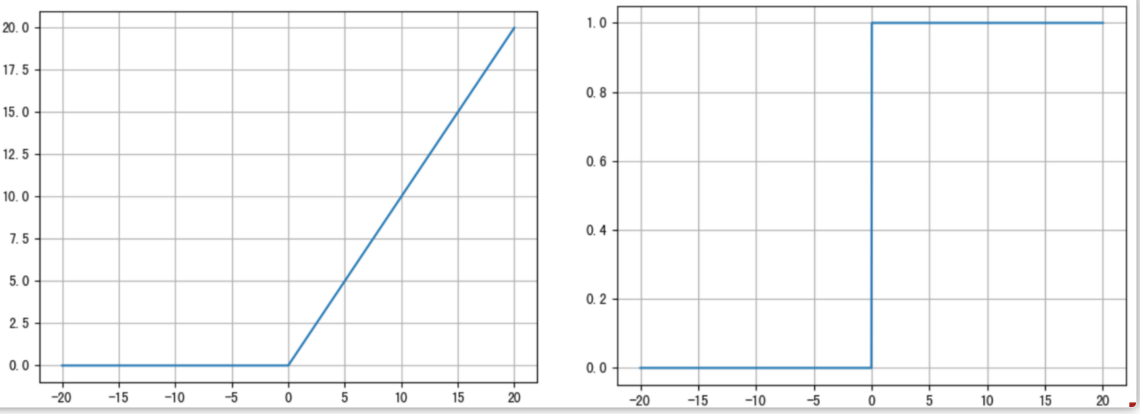
ReLU 的函数图像、导数图像如下:
-
ReLU 激活函数将小于0的值映射为0,而大于0的值则保持不变,它更加重视正信号,而忽略负信号,这种激活函数运算更为简单,能够提高模型的训练效率。
-
当x<0时,ReLU导数为0,而当x>0时,则不存在饱和问题。所以,ReLU 能够在x>0时保持梯度不衰减,从而缓解梯度消失问题。然而,随着训练的推进,部分输入会落入小于0区域,导致对应权重无法更新。这种现象被称为"神经元死亡"。
-
ReLU是目前最常用的激活函数。与sigmoid相比,RELU的优势是:
-
采用sigmoid函数,计算量大(指数运算),反向传播求误差梯度时,计算量相对大;而采用Relu激活函数,整个过程的计算量节省很多
-
sigmoid函数反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练;而采用relu激活函数,当输入的值>0时,梯度为1,不会出现梯度消失的情况
-
Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生
-
SoftMax激活函数
softmax用于多分类 过程中,它是二分类函数sigmoid在多分类上的推广,目的是将多分类的结果以概率的形式展现出来。
计算方法如下图所示:

SoftMax就是将网络输出的logits通过softmax函数,映射成为(0,1)的值,而这些值的累和为1(满足概率的性质),那么我们将它理解成概率,选取概率最大(也就是值对应最大的)节点,作为我们的预测目标类别。
对于隐藏层:
-
优先选择ReLU激活函数
-
如果ReLu效果不好,那么尝试其他激活,如Leaky ReLu等。
-
如果你使用了ReLU, 需要注意一下Dead ReLU问题,避免出现0梯度从而导致过多的神经元死亡。
-
少使用sigmoid激活函数,可以尝试使用tanh激活函数
对于输出层:
-
二分类问题选择sigmoid激活函数
-
多分类问题选择softmax激活函数
-
回归问题选择identity激活函数
在神经网络中,参数的梯度是通过反向传播 (Backpropagation)计算的,其数学基础是链式法则 (Chain Rule)。 对于某一层的权重 W,其梯度为:

反向传播的核心是链式法则。我们以一个简单的全连接前馈网络为例:

🔍 所以:激活函数的导数直接影响梯度的大小和传播效率
🎯 核心结论:
💡 损失函数决定"梯度从哪来",激活函数决定"梯度怎么传"。 两者必须协同设计:
损失函数要能提供有意义的初始梯度;
激活函数要保证这个梯度能顺利回传到前面的层。
💡 因为在反向传播中,梯度是通过链式法则逐层相乘的。如果某层的激活函数导数接近 0,它会把上游梯度"压缩"到极小值。多层连乘后,梯度指数级衰减,导致前面的层无法有效更新,这就是梯度消失。
虽然 Tanh 比 Sigmoid 更优(零中心、导数更大),但它仍然存在梯度消失问题,因此在深层网络中已被 ReLU 等更先进的激活函数取代
整体过程:
-
起点梯度:由损失函数对最后一层激活值求导得到,标志着梯度回传的起始点。
-
逐层梯度计算:每一层的梯度不仅依赖于当前层的激活函数导数,还受到下一层梯度的影响,形成一种递归的关系。
-
参数更新:利用计算出的梯度,采用优化算法(如SGD、Adam等)更新权重和偏置,以最小化损失函数。