原题再现
小度进入了一个迷宫当中,该迷宫为一个 n 个点,m 条边的无向图 ,在开始之前,你需要将每条边规定一个方向。一开始所有的点都是白色,同时小度手中有 k 种不包含白色的不同颜色颜料,小度将从 1 号点出发 ,++每次经过一个点都可以将该点的颜色染色,也可以不进行染色++ ,小度可以随时结束。现在小度想问你,++如何选定边的方向++ 才能使得结束之后,该迷宫生成的不同的迷宫颜色数目最多。在该方案下迷宫颜色数目有多少种可能,由于答案可能过大,答案对 998244353 取模。
对于任意两种迷宫颜色,如果存在一个点的颜色不同,则称该两种迷宫颜色不同。
对于任意两种选定边的方向的方案,如果存在任意一条边的方向不同,则称该两种方案不同。
题意简述
无向图给边定向,使得从1出发染色,最大化迷宫能生成的不同的迷宫颜色数(后简称"颜色数")。
题目解答
最优定向方案
我们要最大化颜色数,就要通过定向使从1出发经过的点最多,因为这样可以自由染色的点的数量就最多。
题目中给出的样例1有4种定向方案:
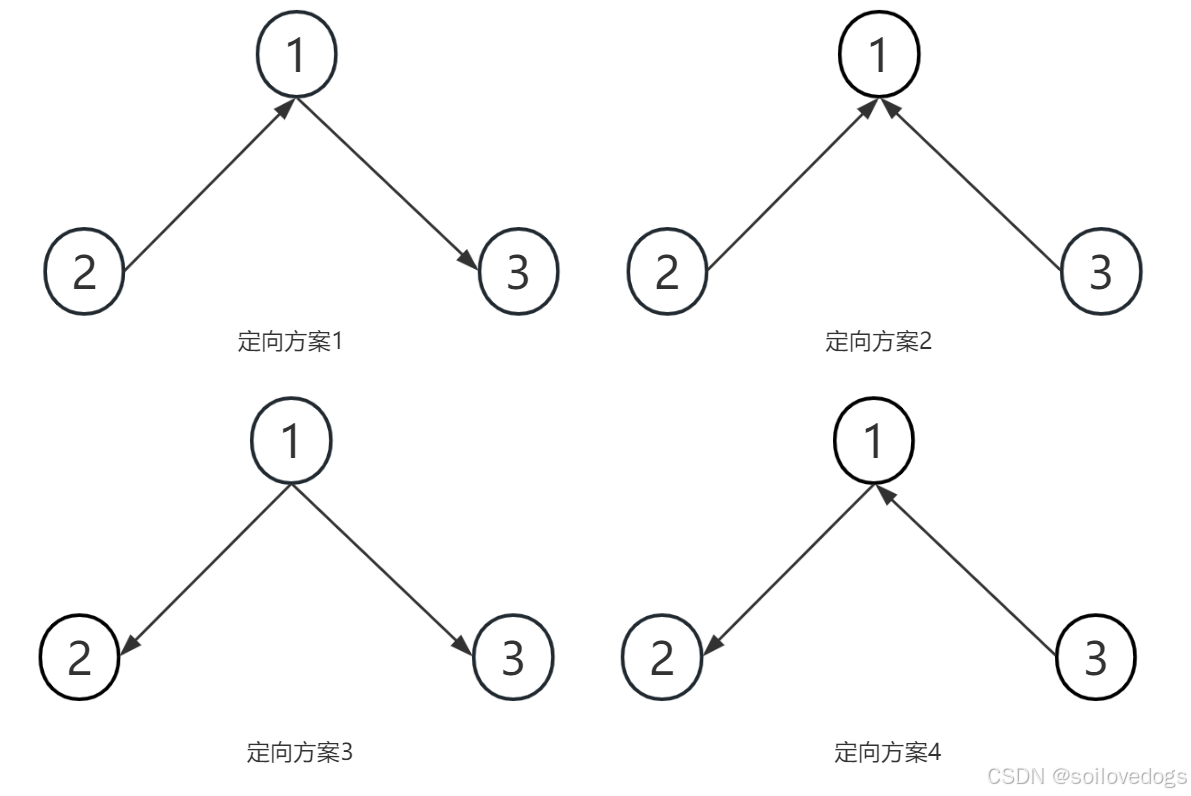
从1出发,我们需要最大化可以自由染色的点的数量,任何"反向"的边都是没有好处的。4种方案可以自由染色的点的数量分别为2,1,3,2,所以选择定向方案3。
对于样例2(自己构造的),按照同样的思路,我们可以确定如下图所示的最优定向方案。
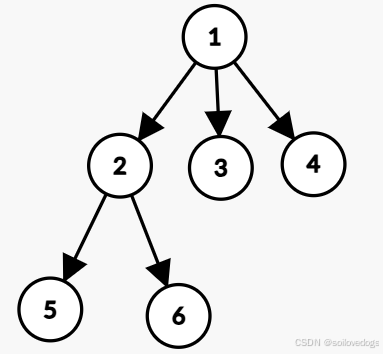
通过这两个例子,我们对最优定向方案已经有了直观的感觉,即边的方向总是"远离"着起点1,而且可以自由染色的点构成一棵树。
考虑特殊的环结构。
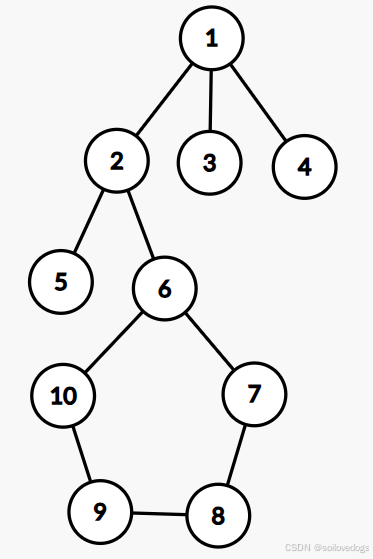
我们应该将环收尾顺次连起来(具体方向无所谓)。因为这样,经过环上任意一点,即可经过环上所有点,实现了经过更多的点的目标。
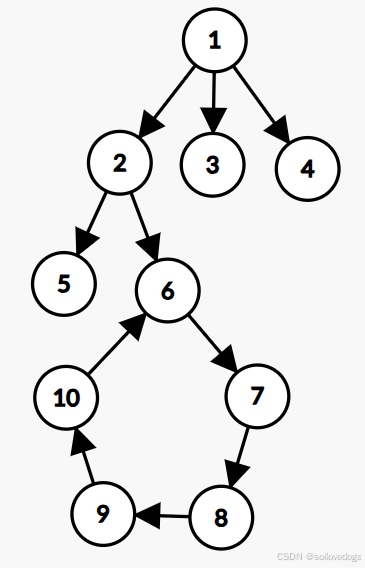
显然,对于环,我们要做缩点操作。
颜色数计算
在确定了最优定向方案之后,我们来计算颜色数。
还是先以样例1为例,根据之前的分析,我们已经确定它的最优定向方案如下图。
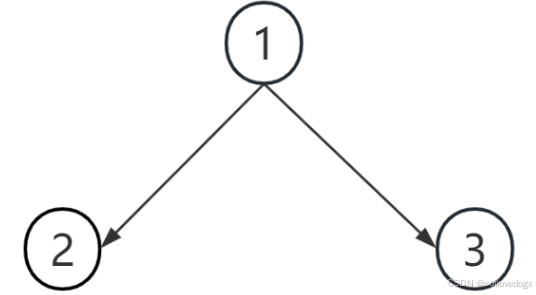
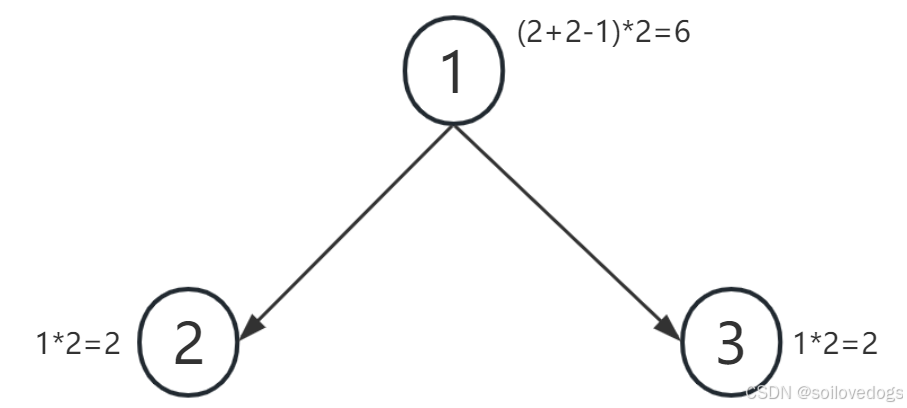
那是怎么得到颜色数6的呢?如下图。
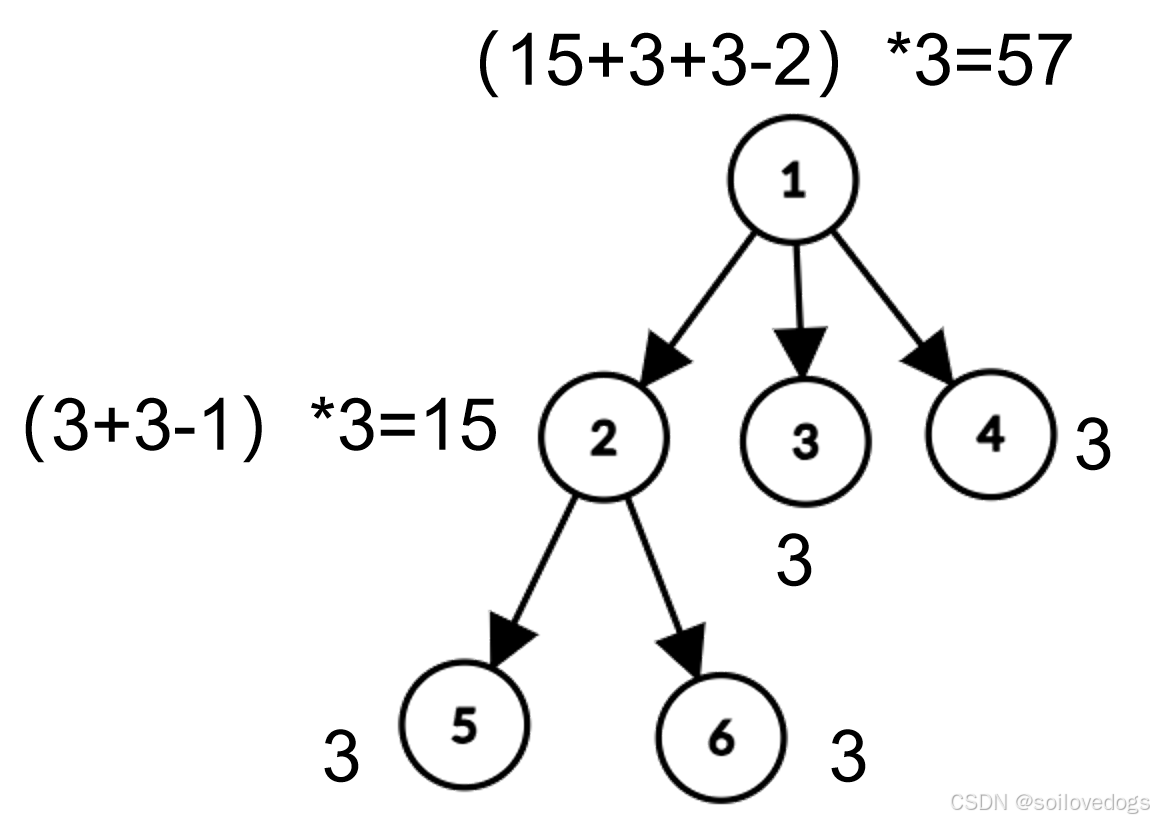
对于样例2,颜色数为16,推导过程见下图。
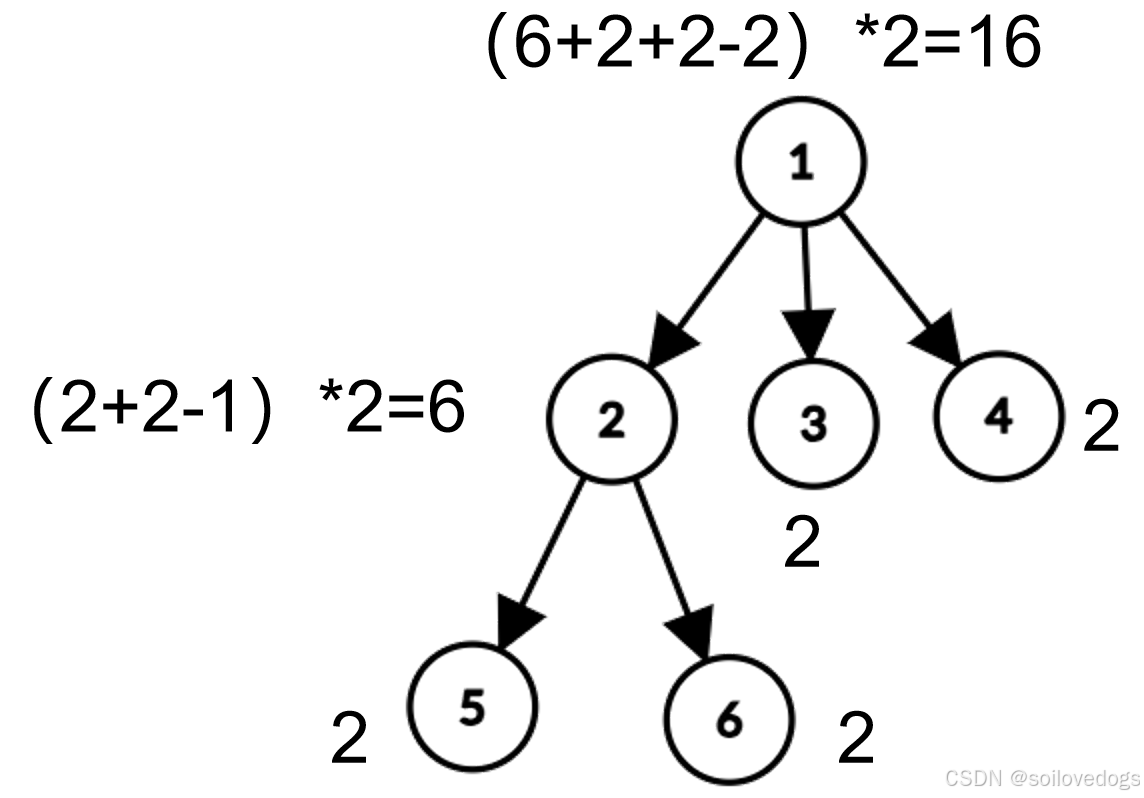
上面两个例子中乘的"2"其实是k+1,代表每个可以自由染色的点的自由度,即"k种颜色+不染色"。比如,如果k=2,样例2中每个可以自由染色的点的自由度变为k+1=3,样例2颜色数变为57,推导过程如下图。