LeetCode189.旋转数组:
题目描述:
思路:
题意是需要我们将数组中的后面k个放到前面,并且使用原地算法。
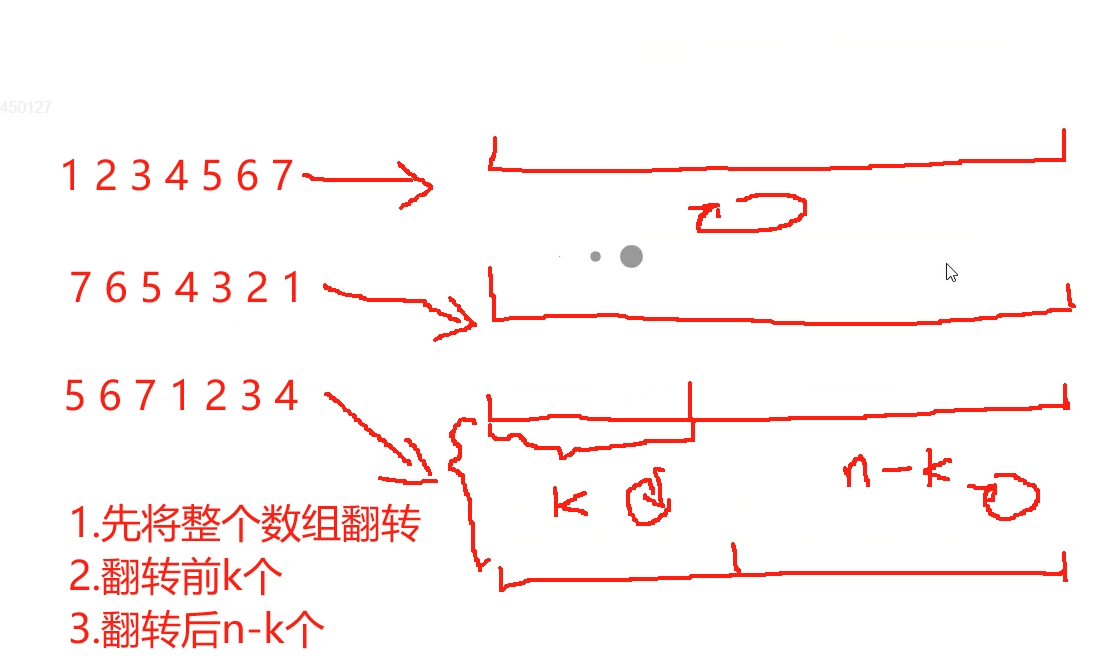
首先使用双指针可以实现原地将整个数组进行翻转,但是这里题意需要我们将后面的k个放到前面,那么可以逆向思维,先将数组翻转,翻转之后的数组整个是倒的,然后先翻转前k个,然后单独翻转后面n-k个
时间复杂度:O(n)
代码:
class Solution {
public:
void rotate(vector<int>& nums, int k) {
int n = nums.size();
k %= n;
reverse(nums.begin(), nums.end());
reverse(nums.begin(), nums.begin() + k);
reverse(nums.begin() + k, nums.end());
}
};LeetCode190.颠倒二进制位:
题目描述:
颠倒给定的 32 位无符号整数的二进制位。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在 示例 2 中,输入表示有符号整数 -3,输出表示有符号整数 -1073741825。
示例 1:
输入:n = 00000010100101000001111010011100
输出:964176192 (00111001011110000010100101000000)
解释:输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596,
因此返回 964176192,其二进制表示形式为 00111001011110000010100101000000。
示例 2:
输入:n = 11111111111111111111111111111101
输出:3221225471 (10111111111111111111111111111111)
解释:输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293,
因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。
提示:
输入是一个长度为 32 的二进制字符串
进阶: 如果多次调用这个函数,你将如何优化你的算法?
思路:
题意是给出32的颠倒的二进制表示,需要求出其正确的二进制表示数值
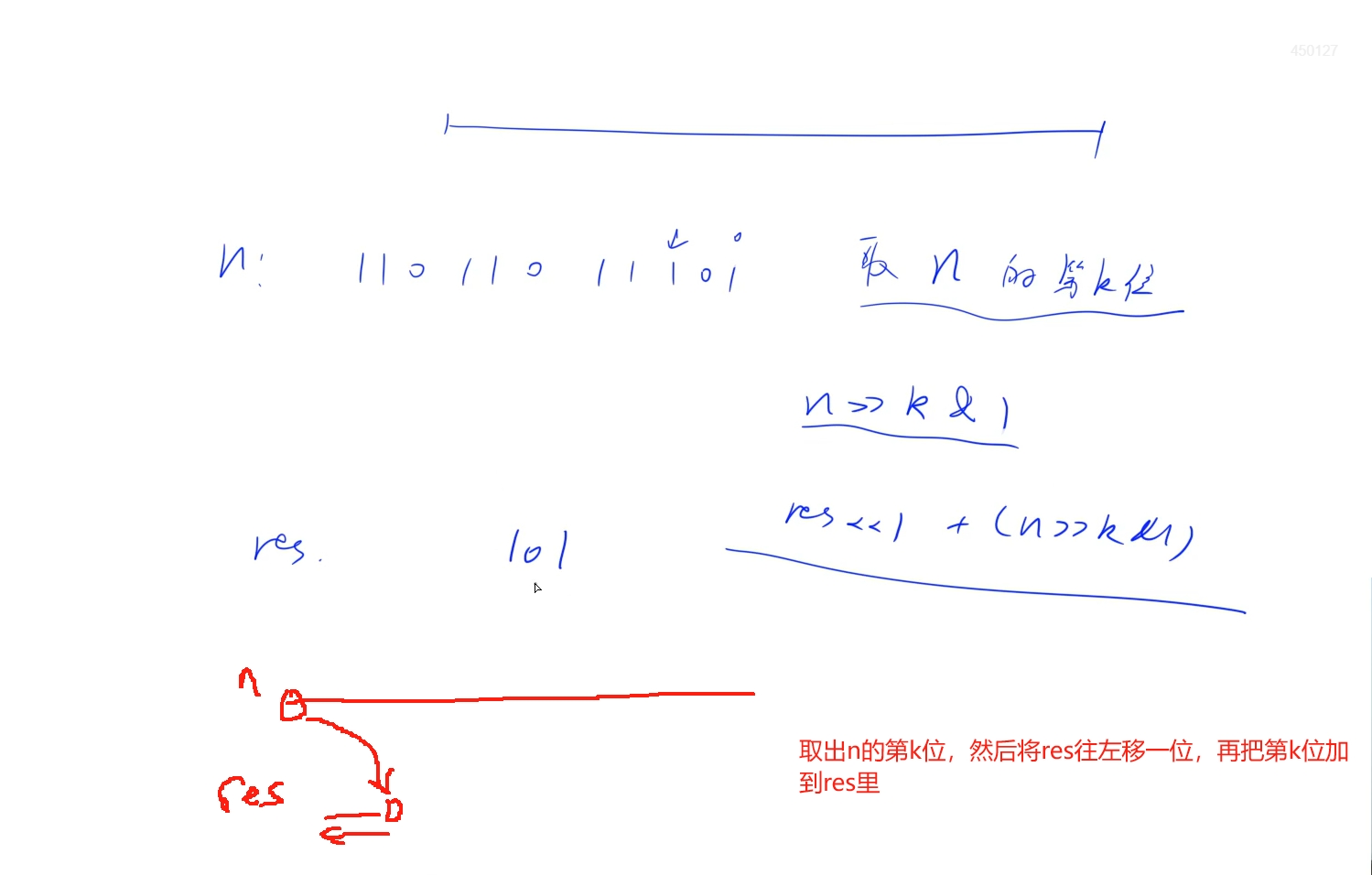
正常做法是先将32位转成string,然后翻转一下再转uint32_t,但是这里可以使用位运算知识直接将给出的颠倒二进制表示直接转成正确的表示数值,颠倒之后,二进制表示就从后往前了,取第k位,然后将它拼到res最后面,这里res需要提前往左移一位
时间复杂度:总共循环32次
代码:
class Solution {
public:
uint32_t reverseBits(uint32_t n) {
uint32_t res = 0;
for(int i = 0; i < 32; i++)
{
res = res * 2 + (n >> i & 1);
}
return res;
}
};LeetCode191.位1的个数:
题目描述:
给定一个正整数 n,编写一个函数,获取一个正整数的二进制形式并返回其二进制表达式中
设置位
的个数(也被称为汉明重量)。
示例 1:
输入:n = 11
输出:3
解释:输入的二进制串 1011 中,共有 3 个设置位。
示例 2:
输入:n = 128
输出:1
解释:输入的二进制串 10000000 中,共有 1 个设置位。
示例 3:
输入:n = 2147483645
输出:30
解释:输入的二进制串 1111111111111111111111111111101 中,共有 30 个设置位。
提示:
1 <= n <= 2^31 - 1
进阶:
如果多次调用这个函数,你将如何优化你的算法?
算法1:
思路:每次看n的最后一位是否位1,同时每次将n右移一位
代码:
class Solution {
public:
int hammingWeight(int n) {
int res = 0;
while(n)
{
res += n & 1;
n >>= 1;
}
return res;
}
};算法2:
思路:
lowbit(x): 返回x的最后一位1,我们每次让x减去lowbit(x)直到0为止,那么能够减多少次,说明有多少个1

代码:
class Solution {
public:
int hammingWeight(int n) {
int res = 0;
while(n) n -= n & -n, res++;
return res;
}
};LeetCode198.打家劫舍:
题目描述:
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 400
思路:
题意: 在给定的一排房屋中不能盗取相邻的两家,安排盗取路径,使得盗取的金额最大
一般这种问最优解,并且路径选择很多的题目,都考虑用Dp来做,这题怎么用Dp呢
首先,第i个位置的状态还得看i-1和i+1的状态,一个状态表示很难顾及,所以使用两个状态数组来表示:
f[i]:从1~i中选,必选i的最大值
g[i]:从1~i中选,必不选i的最大值
状态转移:
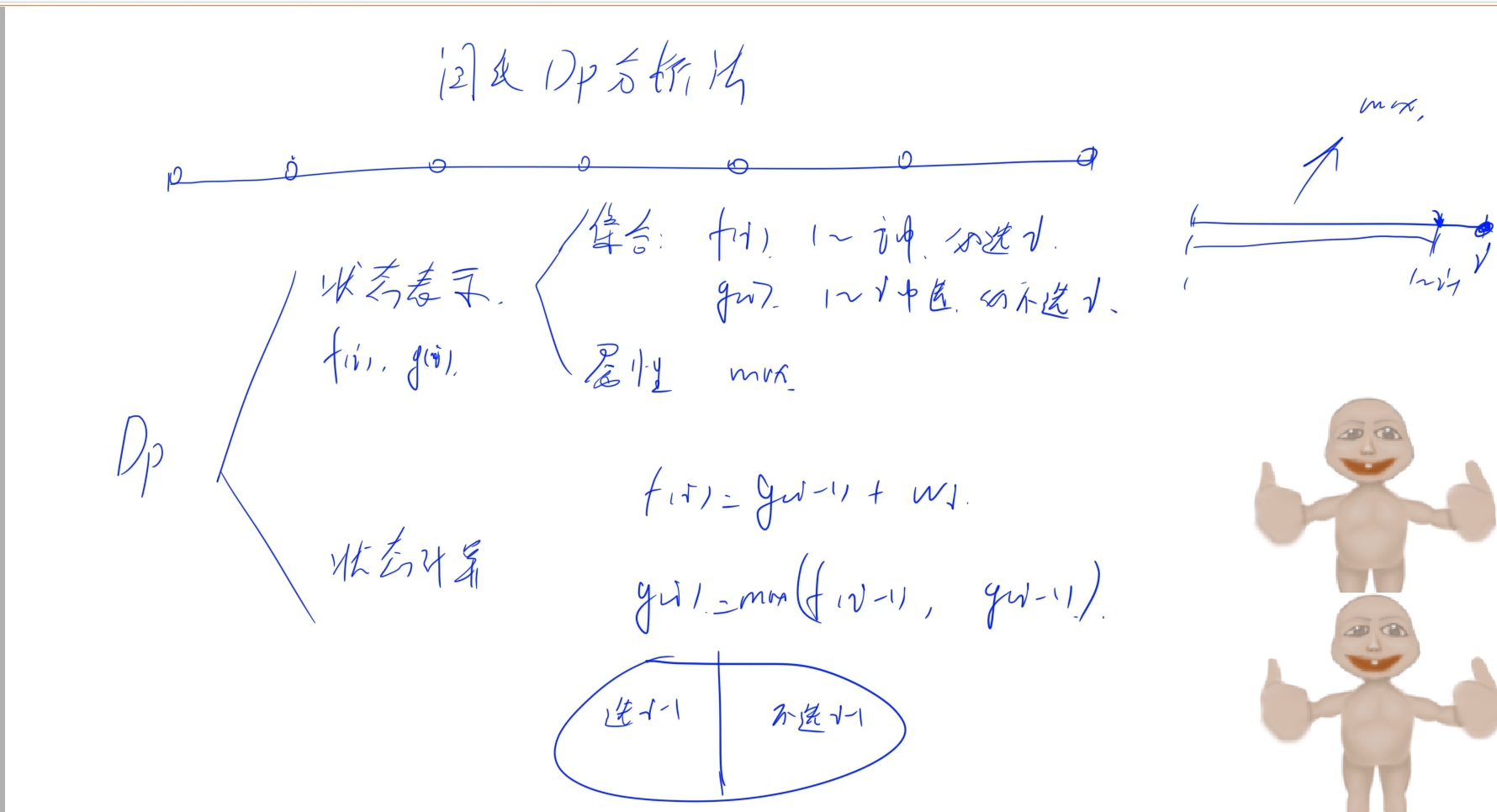
f[i]:第i个位置必选,那么i-1就是必不选(g[i - 1]),所以f[i] = g[i - 1] + w[i]
g[i]: 第i个位置必不选,但是i-1有两种选择:
1.选i-1: 也就是从1~i-1中选必选i-1的最大值(f[i -1])
2.不选i-1: 也就是从1~i-1中选,必不选i-1的最大值(g[i -1])
g[i] = max(f[i -1], g[i - 1])
时间复杂度:O(n)
代码:
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
vector<int> f(n + 1), g(n + 1);
for(int i = 1; i <= n; i++)
{
f[i] = g[i - 1] + nums[i - 1];
g[i] = max(f[i - 1], g[i - 1]);
}
return max(f[n], g[n]);
}
};LeetCode199.二叉树的右视图:
题目描述:
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
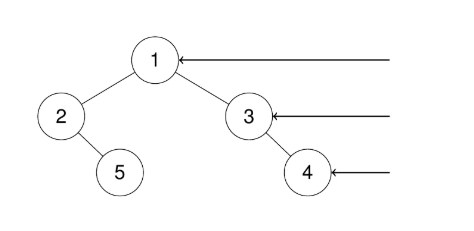
输入:root = [1,2,3,null,5,null,4]
输出:[1,3,4]
解释:
示例 2:
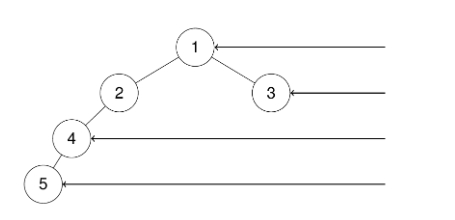
输入:root = [1,2,3,4,null,null,null,5]
输出:[1,3,4,5]
解释:
示例 3:
输入:root = [1,null,3]
输出:[1,3]
示例 4:
输入:root = []
输出:[]
提示:
二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100
思路:
题意:给定一颗二叉树,要从右侧看过来,返回相当于第一列(最右侧)的节点
要将已经会的东西融会贯通,右视图,也就是每一层的最右边的节点,说到每一层,自然逃不开层序遍历,我们只要将层序遍历中每一层的最后一个节点抠出来就是右视图了
时间复杂度:
每个节点进队一次出队一次,每个节点的计算时间消耗是O(1)的,总的时间复杂度为O(n)
注释代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
queue<TreeNode*> q;
vector<int> res;
if(!root) return res;
q.push(root);
while(q.size())
{
int len = q.size();
int temp = 0;
for(int i = 0; i < len; i++)
{
auto root = q.front();
q.pop();
if(root -> left) q.push(root -> left);
if(root -> right) q.push(root -> right);
if(i == len -1) res.push_back(root -> val);
}
}
return res;
}
};LeetCode200.岛屿数量:
题目描述:
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
"1","1","1","1","0"\], \["1","1","0","1","0"\], \["1","1","0","0","0"\], \["0","0","0","0","0"
]
输出:1
示例 2:
输入:grid = [
"1","1","0","0","0"\], \["1","1","0","0","0"\], \["0","0","1","0","0"\], \["0","0","0","1","1"
]
输出:3
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 '0' 或 '1'
思路:
题意就是找到矩阵中连通块的数量
涉及找连通块数量的题,一般使用最常见的flood fill(洪水灌溉算法),使用深搜或者宽搜找到连通块
时间复杂度:O(nm)
注释代码:
class Solution {
public:
vector<vector<char>> g;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, -1, 0, 1};
int numIslands(vector<vector<char>>& grid) {
g = grid;
int cnt = 0;
for(int i = 0; i < grid.size(); i++)
{
for(int j = 0; j < grid[i].size(); j++)
{
if(g[i][j] == '1') //当前格子可以走的话
{
dfs(i, j); //从当前格子延申,直到将所有连通格子走完
cnt++;
}
}
}
return cnt;
}
void dfs(int x, int y)
{
g[x][y] = 0; //标记当前已经走过了
for(int i = 0; i < 4; i++)
{
int a = x + dx[i], b = y + dy[i];
if(a >= 0 && a < g.size() && b >= 0 && b < g[0].size() && g[a][b] == '1') //如果在范围内,并且能走
{
dfs(a, b);
}
}
}
};LeetCode201.数字范围按位与:
题目描述:
给你两个整数 left 和 right ,表示区间 [left, right] ,返回此区间内所有数字 按位与 的结果(包含 left 、right 端点)。
示例 1:
输入:left = 5, right = 7
输出:4
示例 2:
输入:left = 0, right = 0
输出:0
示例 3:
输入:left = 1, right = 2147483647
输出:0
提示:
0 <= left <= right <= 2^31 - 1
思路:

时间复杂度:O(1)
注释代码:
class Solution {
public:
int rangeBitwiseAnd(int m, int n) {
int res = 0;
for(int i = 30; i >= 0; i--)
{
if((m >> i & 1) != (n >> i & 1)) break; //找到m和n从左往右第一个不同的1
if(m >> i & 1) res += 1 << i; //如果当前位为1,则将当前位的原封不动1加到res中
}
return res;
}
};纯享版:
class Solution {
public:
int rangeBitwiseAnd(int m, int n) {
int res = 0;
for(int i = 30; i >= 0; i--)
{
if((m >> i & 1) != (n >> i & 1)) break;
if(m >> i & 1) res += 1 << i;
}
return res;
}
};LeetCode202.快乐数:
题目描述:
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:
输入:n = 2
输出:false
提示:
1 <= n <= 2^31 - 1
思路:
题意是要我们将给定的一个初始数不断将他的每一位单独平方再求和之后看总和是否为1,为1则为快乐数,因为为1之后后面一直都为1了,否则的话就将总和再继续将每一位单独平方再求和,以此循环。如果总和始终不为1则返回false。
首先n为2^23 - 1范围内的数,假设n=9999999999(10个9),是远超范围的,就算如此总和也才(9*9) *10= 810,所以对于任意在范围内的n,它的总和数不断循环求和,也最多会产生812个数,也就是循环812次之后必然会回到某个相同的数以此往复,也就是会形成一个环,所以我们只需要看环中的点是否为1,如果为1肯定环里只有1,因为1不能延展到任何数,以此由之前的环形链表,已经知道怎么找环,就使用快慢指针,当两个指针相遇的时候肯定是在环的某个位置上,这样的话,只要判断相遇时的数是否为1就可以判断了,因为为1就会立马成环,而且环里也只有1。

时间复杂度:O(1),总共循环不到812次
注释代码:
class Solution {
public:
int get(int x) //将一个整数的每一位上的数单独平方再求和
{
int res = 0;
while(x)
{
res += (x % 10) * (x % 10);
x /= 10;
}
return res;
}
bool isHappy(int n) {
int fast = get(n), slow = n; //快指针在前,慢指针在后
while(fast != slow)
{
fast = get(get(fast)); //快指针每次走两次
slow = get(slow); //慢指针走一次
}
return fast == 1; //如果遇到1则会开始成环,因为1的平方还是1
}
};纯享版:
class Solution {
public:
int gets(int n)
{
int res = 0;
while(n)
{
res += (n % 10) * (n % 10);
n /= 10;
}
return res;
}
bool isHappy(int n) {
int fast = gets(n), slow = n;
while(fast != slow)
{
fast = gets(gets(fast));
slow = gets(slow);
}
return fast == 1;
}
};LeetCode203.移除链表元素:
题目描述:
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
示例 1:
输入:head = [1,2,6,3,4,5,6], val = 6
输出:[1,2,3,4,5]
示例 2:
输入:head = [], val = 1
输出:[]
示例 3:
输入:head = [7,7,7,7], val = 7
输出:[]
提示:
列表中的节点数目在范围 [0, 104] 内
1 <= Node.val <= 50
0 <= val <= 50
思路:
题意是将链表中节点值与给定目标值相同的节点移除
链表题一定要画图,不要脑子里想的觉得是这么回事就行,一定画图!!
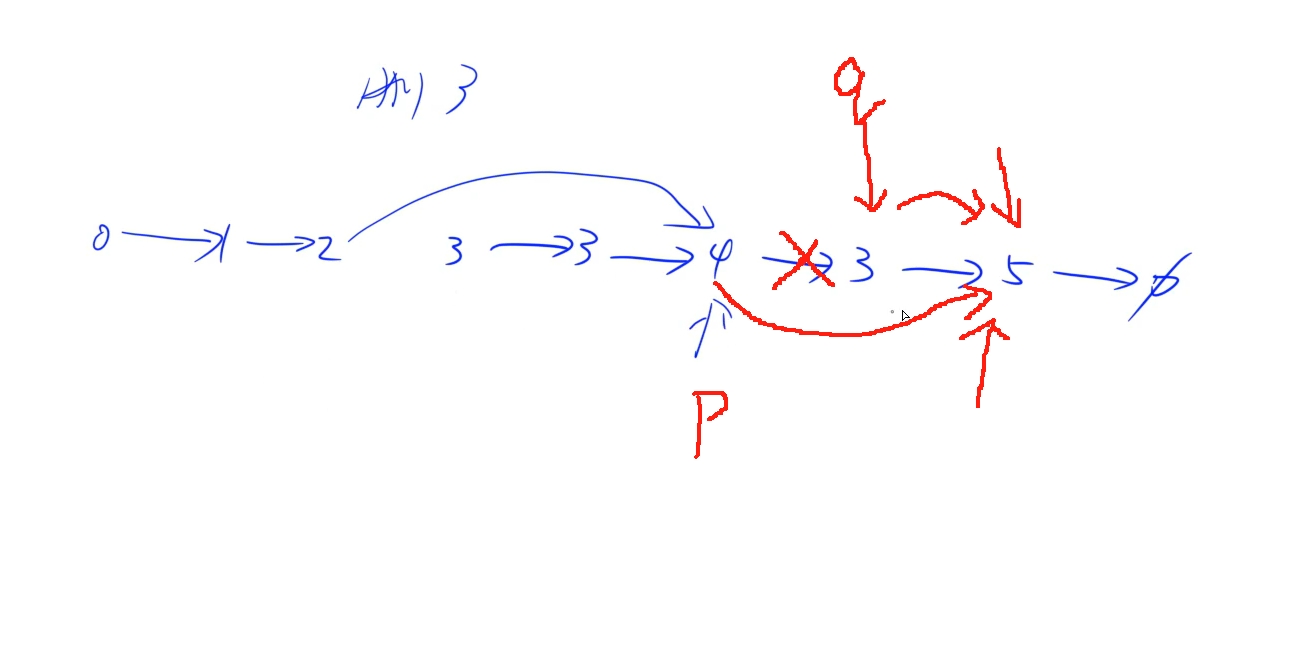
时间复杂度:O(n)
注释代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
auto dummy = new ListNode(-1);
dummy -> next = head;
for(auto p = dummy; p; p = p -> next)
{
auto q = p -> next; //从当前节点的下一个位置开始
while(q && q -> val == val) q = q -> next; //只要存在并且节点值等于目标节点值就跳过
p -> next = q; //直接将当前节点指向跳到的不同位置
}
return dummy -> next;
}
};纯享版:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
auto dummy = new ListNode(-1);
dummy -> next = head;
for(auto p = dummy; p ; p = p -> next)
{
auto q = p -> next;
while(q && q -> val == val) q = q -> next;
p -> next = q;
}
return dummy -> next;
}
};###LeetCode204.计数质数:
##题目描述:
给定整数 n ,返回 所有小于非负整数 n 的质数的数量 。
示例 1:
输入:n = 10
输出:4
解释:小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
示例 2:
输入:n = 0
输出:0
示例 3:
输入:n = 1
输出:0
提示:
0 <= n <= 5 * 10^6
思路:
线性筛法:注意看清题目,是小于n的,而不是1~n
时间复杂度:O(n)
注释代码:
class Solution {
public:
int countPrimes(int n) {
vector<bool> st(n + 1);
vector<int> primes;
for(int i = 2; i < n; i++) //依次枚举每个备选数
{
if(!st[i]) //没有标记为合数的话
{
primes.push_back(i);
}
for(int j = 0; i * primes[j] < n; j++) //枚举质数数组中的每个
{
st[i * primes[j]] = true; //通过最小质因子将所有倍数筛掉
if(i % primes[j] == 0) break;
}
}
return primes.size();
}
};纯享版:
class Solution {
public:
int countPrimes(int n) {
vector<int> primes;
vector<bool> st(n + 1);
for(int i = 2; i < n; i++)
{
if(!st[i]) primes.push_back(i);
for(int j = 0; i * primes[j] < n; j++)
{
st[i * primes[j]] = true;
if(i % primes[j] == 0) break;
}
}
return primes.size();
}
};LeetCode204.计数质数:
题目描述:
给定整数 n ,返回 所有小于非负整数 n 的质数的数量 。
示例 1:
输入:n = 10
输出:4
解释:小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
示例 2:
输入:n = 0
输出:0
示例 3:
输入:n = 1
输出:0
提示:
0 <= n <= 5 * 10^6
思路:
线性筛法:注意看清题目,是小于n的,而不是1~n
时间复杂度:O(n)
注释代码:
class Solution {
public:
int countPrimes(int n) {
vector<bool> st(n + 1);
vector<int> primes;
for(int i = 2; i < n; i++) //依次枚举每个备选数
{
if(!st[i]) //没有标记为合数的话
{
primes.push_back(i);
}
for(int j = 0; i * primes[j] < n; j++) //枚举质数数组中的每个
{
st[i * primes[j]] = true; //通过最小质因子将所有倍数筛掉
if(i % primes[j] == 0) break;
}
}
return primes.size();
}
};纯享版:
class Solution {
public:
int countPrimes(int n) {
vector<int> primes;
vector<bool> st(n + 1);
for(int i = 2; i < n; i++)
{
if(!st[i]) primes.push_back(i);
for(int j = 0; i * primes[j] < n; j++)
{
st[i * primes[j]] = true;
if(i % primes[j] == 0) break;
}
}
return primes.size();
}
};LeetCode205.同构字符串:
题目描述:
给定两个字符串 s 和 t ,判断它们是否是同构的。
如果 s 中的字符可以按某种映射关系替换得到 t ,那么这两个字符串是同构的。
每个出现的字符都应当映射到另一个字符,同时不改变字符的顺序。不同字符不能映射到同一个字符上,相同字符只能映射到同一个字符上,字符可以映射到自己本身。
示例 1:
输入:s = "egg", t = "add"
输出:true
示例 2:
输入:s = "foo", t = "bar"
输出:false
示例 3:
输入:s = "paper", t = "title"
输出:true
提示:
1 <= s.length <= 5 * 10^4
t.length == s.length
s 和 t 由任意有效的 ASCII 字符组成
思路:
题意:两个字符串,看相同位置的字母是否能找到对应的映射,同时需要满足,相同字符映射到同一个字符上,不同字符不能映射到同一个字符上
怎么进行判断呢?
1.首先要判断t串中相同字符是否映射到s串的同一个字符上,就是使用hash表进行判断当前s中的字符是否被映射过了,如果映射过,那么对应的字符是不是t串中当前的字符,如果不是,则说明t串中相同字符没有映射到s串的同一个字符上,如果没有映射过,则将映射保持下来
2.判断t串中的同一个字符不能映射到s串的不同字符上,使用hash表判断t串的当前字符字符映射到s串过,如果映射过,映射的字符是不是当前字符,如果不是,则说明t串的同一个字符映射到了s串的不同字符上
时间复杂度:O(n)
注释代码:
class Solution {
public:
bool isIsomorphic(string s, string t) {
unordered_map<char, char> st, ts;
for(int i = 0; i < s.size(); i++)
{
char a = s[i], b = t[i]; //分别取两个字符串的当前字符
//如果a被映射过,则判断映射过的字母是否为b,如果不是则说明相同字母不是映射到同一个字母上
if(st.count(a) && st[a] != b) return false;
st[a] = b; //否则将t串中的b映射到s串的a上
//如果b被映射过,并且映射的不是a,说明相同字符映射到了不同字母上
if(ts.count(b) && ts[b] != a) return false;
ts[b] = a;
}
return true;
}
};纯享版:
class Solution {
public:
bool isIsomorphic(string s, string t) {
unordered_map<char, char> st, ts;
for(int i = 0; i < s.size(); i++)
{
char a = s[i], b = t[i];
if(st.count(a) && st[a] != b) return false;
st[a] = b;
if(ts.count(b) && ts[b] != a) return false;
ts[b] = a;
}
return true;
}
};LeetCode206.反转链表:
题目描述:
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
示例 2:
输入:head = [1,2]
输出:[2,1]
示例 3:
输入:head = []
输出:[]
提示:
链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000
进阶:链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题?
迭代做法:
时间复杂度:O(n),空间复杂度O(1)
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(!head) return NULL;
auto a = head, b = head -> next;
while(b)
{
auto c = b -> next;
b -> next = a;
a = b;
b = c;
}
head -> next = NULL;
return a;
}
};递归做法:
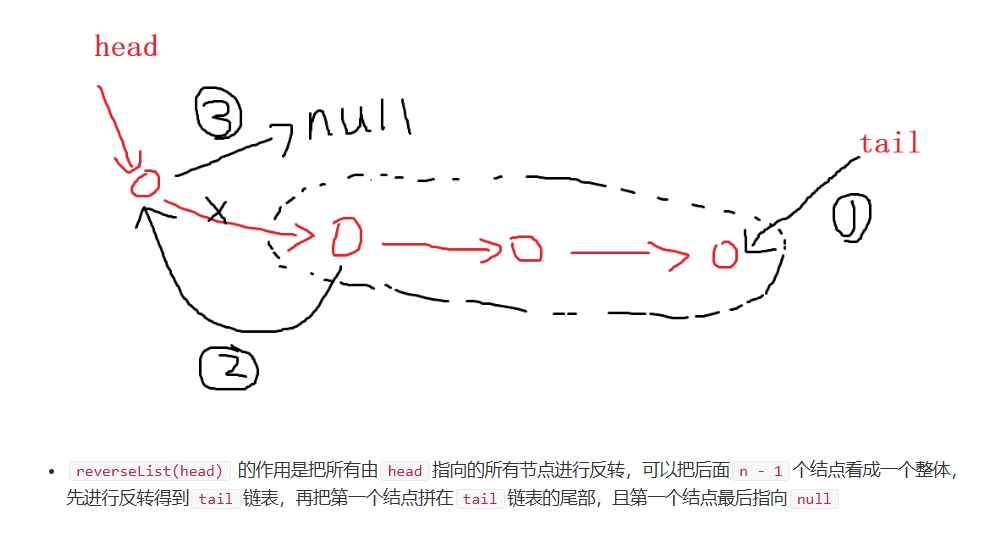
时间复杂度:O(n),空间复杂度O(n)
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(!head || !head -> next) return head;
auto tail = reverseList(head -> next);
head -> next -> next = head;
head -> next = NULL;
return tail;
}
};LeetCode207.课程表:
题目描述:
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
提示:
1 <= numCourses <= 2000
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对 互不相同
思路:图的拓扑序
时间复杂度:
注释代码:
class Solution {
public:
bool canFinish(int n, vector<vector<int>>& edges) {
vector<vector<int>> g(n); //存边
vector<int> d(n); //存每个点的入度
for(auto& e : edges) //对于每条边
{
int b = e[0], a = e[1]; //取出两个点
g[a].push_back(b); //建立a ->b的边
d[b]++; //b的入度+1
}
queue<int> q;
for(int i = 0; i < n; i++)
{
if(d[i] == 0) q.push(i); //将所有入度为0的点加入队列
}
int cnt = 0;
while(q.size())
{
auto t = q.front(); //取出队头
q.pop();
cnt++;
for(auto i : g[t]) //队头连的所有边
{
d[i]--; //入度减1
if(d[i] == 0) q.push(i); //如果入度为0了,说明没有其他先修课了,可以作为起点开始修
}
}
return cnt == n; //判断总共修了几门
}
};纯享版:
class Solution {
public:
bool canFinish(int n, vector<vector<int>>& edges) {
vector<vector<int>> g(n);
vector<int> d(n);
for(auto& e : edges)
{
int b = e[0], a = e[1];
g[a].push_back(b);
d[b]++;
}
queue<int> q;
for(int i = 0; i < n; i++)
{
if(d[i] == 0) q.push(i);
}
int cnt = 0;
while(q.size())
{
auto t = q.front();
q.pop();
cnt++;
for(auto i : g[t])
{
d[i]--;
if(d[i] == 0) q.push(i);
}
}
return cnt == n;
}
};LeetCode208.实现Trie(前缀树)
题目描述:
Trie(发音类似 "try")或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补全和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
示例:
输入
"Trie", "insert", "search", "search", "startsWith", "insert", "search"
\[\], \["apple"\], \["apple"\], \["app"\], \["app"\], \["app"\], \["app"\]
输出
null, null, true, false, true, null, true
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True
提示:
1 <= word.length, prefix.length <= 2000
word 和 prefix 仅由小写英文字母组成
insert、search 和 startsWith 调用次数 总计 不超过 3 * 10^4 次
思路:
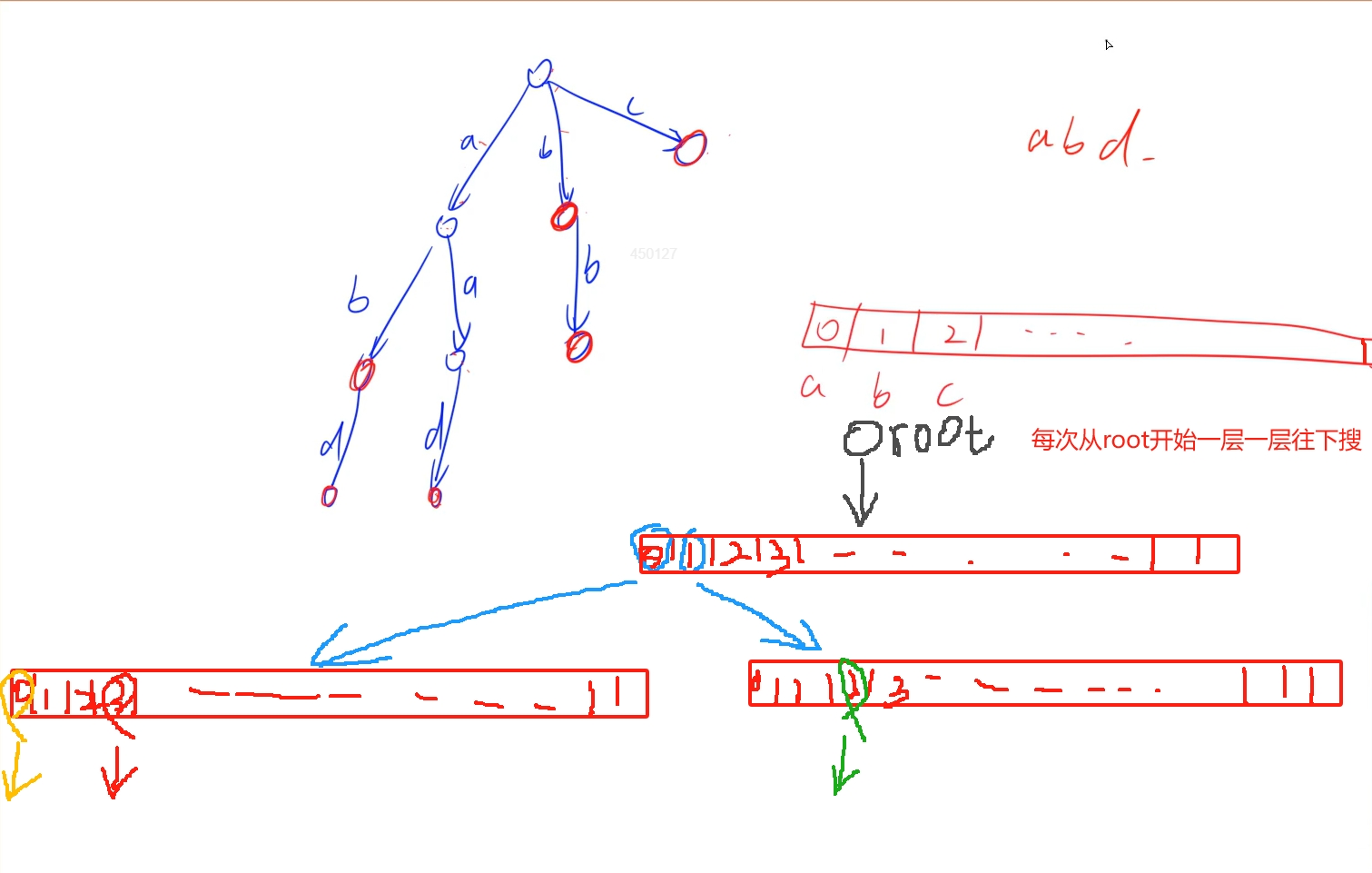
时间复杂度:O(n)
注释代码:
class Trie {
public:
struct Node{
bool is_end;
Node *son[26]; //给每个节点定义26个儿子节点
Node(){
is_end = false;
for(int i = 0; i < 26; i++) //该节点下会创建26个空儿子
{
son[i] = NULL;
}
}
}*root; //先创建父节点
Trie() {
root = new Node();
}
void insert(string word) {
auto p = root;
for(auto c : word)
{
int u = c - 'a'; //将字符映射到0~25
if(!p -> son[u]) p -> son[u] = new Node(); //如果当前路径的字符下没有该儿子节点则创建
p = p -> son[u];
}
p -> is_end = true; //将 该单词的结束位置打上标记
}
bool search(string word) {
auto p = root;
for(auto c : word)
{
int u = c - 'a';
if(!p -> son[u]) return false;
p = p -> son[u]; //存在则往儿子节点走
}
return p -> is_end; //最后返回是否存在以p为结尾的完整路径
}
bool startsWith(string prefix) {
auto p = root;
for(auto c : prefix)
{
int u = c - 'a';
if(!p -> son[u]) return false;
p = p -> son[u];
}
return true; //只要能搜到路径就返回true,不需要判断是否标记
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/纯享版:
class Trie {
public:
struct Node{
bool is_end;
Node *son[26];
Node(){
is_end = false;
for(int i = 0; i < 26; i++)
{
son[i] = NULL;
}
}
}*root;
Trie() {
root = new Node();
}
void insert(string word) {
auto p = root;
for(auto c : word)
{
int u = c - 'a';
if(!p -> son[u]) p -> son[u] = new Node();
p = p -> son[u];
}
p -> is_end = true;
}
bool search(string word) {
auto p = root;
for(auto c : word)
{
int u = c - 'a';
if(!p -> son[u]) return false;
p = p -> son[u];
}
return p -> is_end;
}
bool startsWith(string prefix) {
auto p = root;
for(auto c : prefix)
{
int u = c - 'a';
if(!p -> son[u]) return false;
p = p -> son[u];
}
return true;
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/LeetCode209.长度最小的子数组:
题目描述:
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的
子数组
numsl, numsl+1, ..., numsr-1, numsr\] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。 示例 1: 输入:target = 7, nums = \[2,3,1,2,4,3
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 10^9
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^4
进阶:
如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。
思路:
题意:给定一个正整数数组,要你找出其中元素和大于等于target的子数组(连续的非空子序列),求里面的最短的
首先考虑暴力做法:使用双重循环
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int res = INT_MAX;
for(int i = 0; i < nums.size(); i++){
int sum = 0;
for(int j = i; j < nums.size(); j++)
{
sum += nums[j];
if(sum >= target) res = min(res, j - i + 1);
}
}
if(res == INT_MAX) res = 0;
return res;
}
};但是数组长度为1e5,双重循环肯定TLE,所以思考如何优化,这里可以发现由于都是正整数,当我们遍历数组求子数组和时,当i往后移动,j一定也往后移,所以存在单调性,可以使用双指针算法进行优化
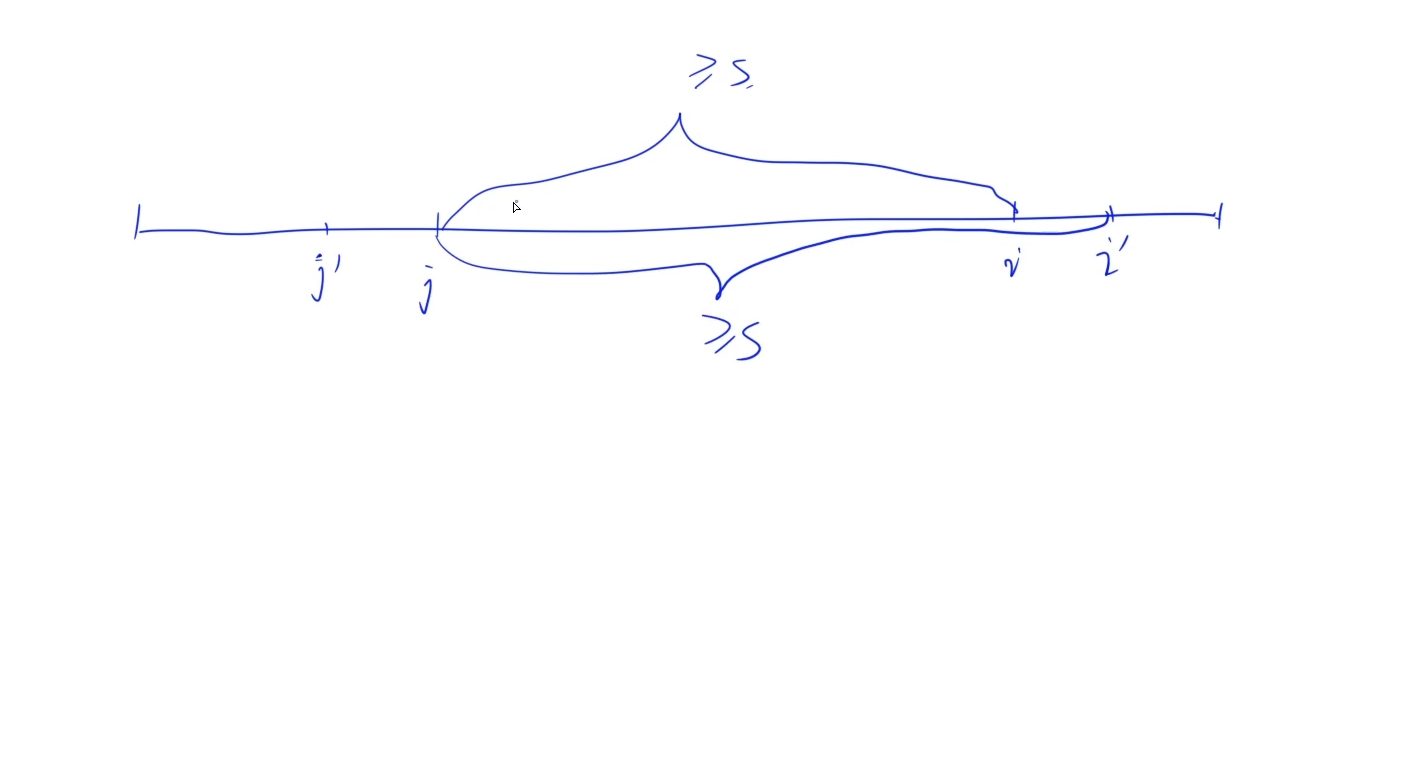
时间复杂度:O(n)
注释代码:
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int res = INT_MAX;
for(int i = 0, j = 0, sum = 0; i < nums.size(); i++)
{
sum += nums[i];
//如果当前范围内减去nums[j]还是满足条件的则将逐渐往右移
//找到距离当前i的最近的j
while(sum - nums[j] >= target) sum -= nums[j++];
if(sum >= target) res = min(res, i - j + 1); //如果满足条件则记录最小的长度
}
if(res == INT_MAX) res = 0; //如果全部都没有符合条件的子数组,那么只能返回0
return res;
}
};纯享版:
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int res = INT_MAX;
for(int i = 0, j = 0, sum = 0; i < nums.size(); i++)
{
sum += nums[i];
while(sum - nums[j] >= target) sum -= nums[j++];
if(sum >= target) res = min(res, i - j + 1);
}
if(res == INT_MAX) return 0;
return res;
}
};LeetCode210.课程表Ⅱ:
题目描述:
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。
例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示:[0,1] 。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
示例 2:
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出:[0,2,1,3]
解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
示例 3:
输入:numCourses = 1, prerequisites = []
输出:[0]
提示:
1 <= numCourses <= 2000
0 <= prerequisites.length <= numCourses * (numCourses - 1)
prerequisites[i].length == 2
0 <= ai, bi < numCourses
ai != bi
所有[ai, bi] 互不相同
思路:
跟 LeetCode207.课程表 是一样的,只不过需要将拓扑序列记录下来
时间复杂度:O(n)
注释代码:
class Solution {
public:
vector<int> findOrder(int n, vector<vector<int>>& edges) {
vector<vector<int>> g(n);
vector<int> d(n);
for(auto e : edges)
{
int b = e[0], a = e[1];
g[a].push_back(b);
d[b]++;
}
queue<int> q;
for(int i = 0; i < n; i++)
{
if(d[i] == 0) q.push(i);
}
vector<int> res;
while(q.size())
{
auto t = q.front();
q.pop();
res.push_back(t); //将当前的点保存
for(auto c : g[t]) //枚举队头的邻边
{
d[c]--;
if(d[c] == 0) q.push(c);
}
}
if(res.size() < n) res = {};
return res;
}
};LeetCode211.添加与搜索单词-数据结构设计:
题目描述;
请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。
实现词典类 WordDictionary :
WordDictionary() 初始化词典对象
void addWord(word) 将 word 添加到数据结构中,之后可以对它进行匹配
bool search(word) 如果数据结构中存在字符串与 word 匹配,则返回 true ;否则,返回 false 。word 中可能包含一些 '.' ,每个 . 都可以表示任何一个字母。
示例:
输入:
"WordDictionary","addWord","addWord","addWord","search","search","search","search"
\[\],\["bad"\],\["dad"\],\["mad"\],\["pad"\],\["bad"\],\[".ad"\],\["b..."\]
输出:
null,null,null,null,false,true,true,true
解释:
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // 返回 False
wordDictionary.search("bad"); // 返回 True
wordDictionary.search(".ad"); // 返回 True
wordDictionary.search("b..."); // 返回 True
提示:
1 <= word.length <= 25
addWord 中的 word 由小写英文字母组成
search 中的 word 由 '.' 或小写英文字母组成
最多调用 10^4 次 addWord 和 search
思路:
题意:实现两个函数,addWord存储单词到word Dictionary中,search在wordDictionary中查找指定单词,但是查找的word包含.意思就是说.能匹配任意字符。
如果查找单词不包含.那么就跟Trie树一样的操作,但是这里需要匹配通配符,那么该如何查找,对于一个.来说有26种可能,如果连续的.那么次数会是26的k次方,非常恐怖,于是考虑使用爆搜,来降低时间复杂度,也就是当搜索到word的第i个字符时,如果不是'.'那么则按Trie树一样正常搜索,如果当前第i个字符是'.'那么则有26种路径,当它的儿子存在并且沿着儿子往i+1搜最终能搜到该单词,则说明存在,否则最终返回false。
时间复杂度:
注释代码:
class WordDictionary {
public:
struct Node{
bool is_end;
Node *son[26];
Node() {
is_end = false;
for(int i = 0; i < 26; i++)
{
son[i] = NULL;
}
}
}*root;
WordDictionary() {
root = new Node();
}
void addWord(string word) {
auto p = root;
for(auto c : word)
{
int u = c - 'a';
if(!p -> son[u]) p -> son[u] = new Node();
p = p -> son[u];
}
p -> is_end = true;
}
bool search(string word) {
return dfs(root, word, 0);
}
//从哪里开始搜,搜索word的第i个字符
bool dfs(Node* p, string& word, int i)
{
if(i == word.size()) return p -> is_end;
if(word[i] != '.')
{
int u = word[i] - 'a';
if(!p -> son[u]) return false;
return dfs(p -> son[u], word, i + 1);
}else{ //如果为.,则将p下面的26个儿子全部搜索一遍
for(int j = 0; j < 26; j++)
{
//如果该儿子存在,并且沿着当前字符的下一个字符往下搜能找到路径,则返回true
if(p -> son[j] && dfs(p -> son[j], word, i + 1))
{
return true;
}
}
return false;
}
}
};
/**
* Your WordDictionary object will be instantiated and called as such:
* WordDictionary* obj = new WordDictionary();
* obj->addWord(word);
* bool param_2 = obj->search(word);
*/纯享版:
class WordDictionary {
public:
struct Node{
bool is_end;
Node *son[26];
Node(){
is_end = false;
for(int i = 0; i < 26; i++) son[i] = NULL;
}
}*root;
WordDictionary() {
root = new Node();
}
void addWord(string word) {
auto p = root;
for(auto c : word)
{
auto u = c - 'a';
if(!p -> son[u]) p -> son[u] = new Node();
p = p -> son[u];
}
p -> is_end = true;
}
bool search(string word) {
return dfs(root, word, 0);
}
bool dfs(Node* p, string& word, int i)
{
if(i == word.size()) return p -> is_end;
if(word[i] != '.')
{
int u = word[i] - 'a';
if(!p -> son[u]) return false;
return dfs(p -> son[u], word, i + 1);
}else
{
for(int j = 0; j < 26; j++)
{
if(p -> son[j] && dfs(p -> son[j], word, i + 1)) return true;
}
return false;
}
}
};
/**
* Your WordDictionary object will be instantiated and called as such:
* WordDictionary* obj = new WordDictionary();
* obj->addWord(word);
* bool param_2 = obj->search(word);
*/LeetCode212.单词搜索Ⅱ:
题目描述:
给定一个 m x n 二维字符网格 board 和一个单词(字符串)列表 words, 返回所有二维网格上的单词 。
单词必须按照字母顺序,通过 相邻的单元格 内的字母构成,其中"相邻"单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。
示例 1:
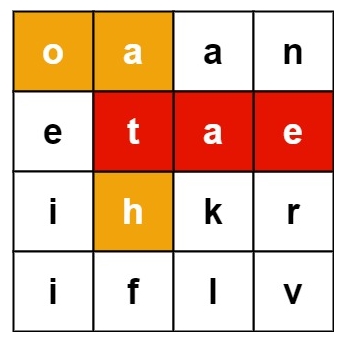
输入:board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
输出:["eat","oath"]
示例 2:
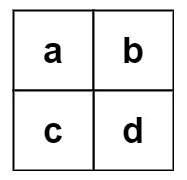
输入:board = [["a","b"],["c","d"]], words = ["abcb"]
输出:[]
提示:
m == board.length
n == board[i].length
1 <= m, n <= 12
board[i][j] 是一个小写英文字母
1 <= words.length <= 3 * 10^4
1 <= words[i].length <= 10
words[i] 由小写英文字母组成
words 中的所有字符串互不相同
思路:
题意:给出一个字符网格,只能往相邻的格子走,看能找到给定words中的哪些单词,需要列出单词
这题就是Trie树和爆搜的结合题,首先呢将所有单词放入Trie树中,然后再使用dfs以字符网格的每一个格子作为起点开始进行爆搜,如果搜到的位置是Trie树中没有的则无需再往下搜了
时间复杂度:

注释代码:
class Solution {
public:
struct Node{
int id;
Node *son[26];
Node(){
id = -1;
for(int i = 0; i < 26; i++)
{
son[i] = NULL;
}
}
}*root;
unordered_set<int> ids;
vector<vector<char>> g;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
void insert(string& word, int id) //将传入的word添加到Trie树中,并记录对应的id
{
auto p = root;
for(auto c : word)
{
int u = c - 'a';
if(!p -> son[u]) p -> son[u] = new Node();
p = p -> son[u];
}
p -> id = id;
}
vector<string> findWords(vector<vector<char>>& board, vector<string>& words) {
g = board;
root = new Node();
for(int i = 0; i < words.size(); i++) insert(words[i], i); //将每个单词插入Trie树中,并记录id
for(int i = 0; i < g.size(); i++)
{
for(int j = 0; j < g[0].size(); j++)
{
int u = g[i][j] - 'a'; //从每个位置开始往下搜
if(root -> son[u]) dfs(i, j, root -> son[u]); //如果存在根节点下存在该路径,则沿着往下搜索
}
}
vector<string> res;
for(auto id : ids) res.push_back(words[id]); //枚举能搜索到的所有单词
return res;
}
void dfs(int x, int y, Node* p)
{
//如果id不为-1则说明是能搜索到的
if(p -> id != -1) ids.insert(p -> id);
char t = g[x][y];
g[x][y] = '.';
for(int i = 0; i < 4; i++)
{
int a = x + dx[i], b = y + dy[i];
if(a >= 0 && a < g.size() && b >= 0 && b < g[0].size() && g[a][b] != '.')
{
int u = g[a][b] - 'a';
if(p -> son[u]) dfs(a, b, p -> son[u]); //如果Trie树中存在该儿子,则往下继续搜索
}
}
g[x][y] = t; //恢复现场
}
};纯享版:
class Solution {
public:
struct Node{
int id;
Node *son[26];
Node(){
id = -1;
for(int i = 0; i < 26; i++) son[i] = NULL;
}
}*root;
unordered_set<int> ids;
vector<vector<char>> g;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
void insert(string& word, int id)
{
auto p = root;
for(auto c : word)
{
int u = c - 'a';
if(!p -> son[u]) p -> son[u] = new Node();
p = p -> son[u];
}
p -> id = id;
}
vector<string> findWords(vector<vector<char>>& board, vector<string>& words) {
root = new Node();
g = board;
for(int i = 0; i < words.size(); i++) insert(words[i], i);
for(int i = 0; i < g.size(); i++)
{
for(int j = 0; j < g[0].size(); j++)
{
int u = g[i][j] - 'a';
if(root -> son[u]) dfs(i, j, root -> son[u]);
}
}
vector<string> res;
for(auto id : ids) res.push_back(words[id]);
return res;
}
void dfs(int x, int y, Node* p)
{
if(p -> id != -1) ids.insert(p -> id);
auto t = g[x][y];
g[x][y] = '.';
for(int i = 0; i < 4; i++)
{
int a = x + dx[i], b = y + dy[i];
if(a >= 0 && a < g.size() && b >= 0 && b < g[0].size() && g[a][b] != '.')
{
int u = g[a][b] - 'a';
if(p -> son[u]) dfs(a, b, p -> son[u]);
}
}
g[x][y] = t;
}
};LeetCode213.打家劫舍Ⅱ:
题目描述:
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:nums = [1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:
输入:nums = [1,2,3]
输出:3
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 1000
思路:
题意: 与打家劫舍Ⅰ不同的是,这里是一个环状的房屋,第一家和第n家是相邻的,现在需要你制定路线盗取最大金额
仔细琢磨会发现,跟打家劫舍Ⅰ不同之处就在于他这里的1号点和n号点不能同时选,那么对于两个对立的点,只需要先确定一个点选不选,另外一个点的情况就能很好的分析出来:
首先在打家劫舍Ⅰ中,使用f[i]表示必选第i个点时的最大收益,g[i]则表示必不选第i个点时的最大收益:
f[i] = g[i - 1] + w[i](必选当前i点,则i- 1 必不能选,收益为不选i-1的最大收益加上当前点的收益)
g[i] = max(f[i - 1], g[i - 1])(必不选当前点,那么i-1号点就可以选f[i-1]或者不选g[i-1])
回到这题:
1.1号点不选: 那么n号点可以选择选f[n]或者不选g[n],二者取最大值:res= max(f[n], g[n]);
2.选1号点: 那么n号点不能选g[n],最终的答案与上一种情况取最大值: res= max(res, f[n]`);

时间复杂度:O(n)
注释代码:
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
if(!n) return 0;
if(n == 1) return nums[0];
vector<int> f(n + 1), g(n + 1);
int res = 0;
//必不选第一个房屋
for(int i = 2; i <= n; i++)
{
f[i] = g[i - 1] + nums[i - 1];
g[i] = max(f[i - 1], g[i - 1]);
}
res = max(f[n], g[n]);
//选第一个房屋,也就是第n个必不能选
f[1] = nums[0];
g[0] = INT_MIN;
for(int i = 2; i <= n; i++)
{
f[i] = g[i - 1] + nums[i - 1];
g[i] = max(f[i - 1], g[i - 1]);
}
res = max(res, g[n]);
return res;
}
};纯享版:
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
if(!n) return 0;
if(n == 1) return nums[0];
vector<int> f(n + 1), g(n + 1);
for(int i = 2; i <= n; i++)
{
f[i] = g[i - 1] + nums[i - 1];
g[i] = max(f[i - 1], g[i - 1]);
}
int res = max(f[n], g[n]);
f[1] = nums[0];
g[1] = INT_MIN;
for(int i = 2; i <= n; i++)
{
f[i] = g[i - 1] + nums[i - 1];
g[i] = max(f[i - 1], g[i - 1]);
}
res = max(res, g[n]);
return res;
}
};LeetCode214.最短回文串:
题目描述:
给定一个字符串 s,你可以通过在字符串前面添加字符将其转换为
回文串
。找到并返回可以用这种方式转换的最短回文串。
示例 1:
输入:s = "aacecaaa"
输出:"aaacecaaa"
示例 2:
输入:s = "abcd"
输出:"dcbabcd"
提示:
0 <= s.length <= 5 * 10^4
s 仅由小写英文字母组成
思路:
题意:给一个字符串要求在前面添加最少的字符使其变成回文串
可以看到在给出的示例中字符串是前面可能已经存在部分回文子串了,如果在前面添加字符的话,相当于添加完之后,以前半段的回文串中间为划分界限,添加的字符是除回文前缀之后的后半段字符串的翻转,那么现在求添加字符最少,也就是要后半段的字符串最短即求最长的前缀回文串,如何求最长的前缀回文串? 将原字符串翻转,中间以特殊符号隔开拼接在原字符串后面,因为前缀的是回文串,翻转之后也是相同的,那么问题也就变成求前缀和后缀相同的最长长度,这就引出经典的KMP算法,利用KMP能求出最大的前缀和后缀相等的长度。在求出最大的长度就是原字符串中最长前缀回文串长度,截取原字符串的后段字符串进行翻转拼接在原字符串前面即是答案。
时间复杂度:
注释代码:
class Solution {
public:
string shortestPalindrome(string s) {
string t(s.rbegin(), s.rend()); //将原串翻转
int n = s.size();
s = ' ' + s + '#' + t; //KMP从1开始比较好写
vector<int> ne(n * 2 + 2);
for(int i = 2, j = 0; i <= 2 * n + 1; i++) //使用KMP求ne数组
{
while(j && s[i] != s[j + 1]) j = ne[j];
if(s[i] == s[j + 1]) j++;
ne[i] = j;
}
int len = ne[2 * n + 1];
//left为前段的最长前缀回文串,right为后面不是回文的字符串
string left = s.substr(1, len), right = s.substr(1 + len, n - len);
//最后返回翻转之后的后部分加上原来的字符串
return string(right.rbegin(), right.rend()) + left + right;
}
};纯享版:
class Solution {
public:
string shortestPalindrome(string s) {
int n = s.size();
string t(s.rbegin(), s.rend());
s = ' ' + s + '#' + t;
vector<int> ne(2 * n + 2);
for(int i = 2, j = 0; i <= 2 * n + 1; i++)
{
while(j && s[i] != s[j + 1]) j = ne[j];
if(s[i] == s[j + 1]) j++;
ne[i] = j;
}
int len = ne[2 * n + 1];
string left = s.substr(1, len), right = s.substr(len + 1, n - len);
return string(right.rbegin(), right.rend()) + left + right;
}
};*注:上述题解图片以及思路均来自acwing学习网站,仅作为交流学习,不作为商业用途,如有侵权,联系删除。