有序矩阵中第K小的元素+二分查找

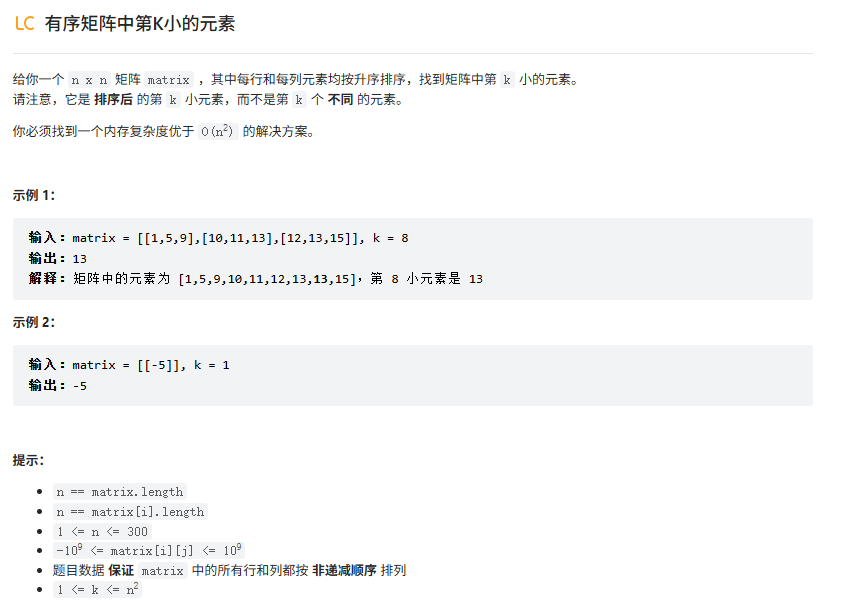
题目：

思考：

1. 最直观的思路是不管矩阵性质，直接遍历后排序（二维变一维）但这复杂度太高且完全没有利用矩阵中相对有序的性质
2. 第二种思路是拆分，n×n的矩阵，拆分成n个一维向量，这些一维向量都是有序的，相当于n个有序数组中找到第k小的，可以使用合并n个有序列表的方法，比如归并排序
3. 但是第二种只使用到了有序矩阵中一个方向上的有序性质
4. 使用二分查找，矩阵中最小的是matrix[0][0]设为min，最大的是matrix[n-1][n-1]设为max,利用二分查找实时查找矩阵中比（min+max）/2小的数的个数，刚好k个就找到了，小于k个说明真正的第k小元素要比（min+max）/2大，更新min的值，同理大于k个更新max的值
5. 那么方法的重难点就在于查找比（min+max）/2小的数的个数，可以遍历每一行去找，但还是要利用矩阵性质，从矩阵右上角开始找，相当于 240. 搜索二维矩阵 II 的方法

实现：

class Solution {
public:
    int kthSmallest(vector<vector<int>>& matrix, int k) {
        int n=matrix.size();
        auto getCount=[&] (int mid)->int
        {
            int count=0;
            int x=0;
            int y=n-1;
            while(y>-1&&x<n)
            {
                if (matrix[x][y]<=mid)
                {
                    count+=y+1;
                    x++;
                }
                else
                {
                    y--;
                }
            }

            return count;
        };



        int l=matrix[0][0];
        int r=matrix[n-1][n-1];
        while(l<=r)
        {
            int mid=(l+r)/2;
            int count=getCount(mid);
            if (count<k)
            {
                l=mid+1;
            }
            else
            {
                r=mid-1;
            }
        }

        return l;
    }
};