动手学深度学习笔记
使用jupyter notebook
-
在已有conda和python的情况下,在新建的项目代码文件夹地址栏键入cmd,跳转至命令行窗口,输入jupyter notebook即可打开jupyter notebook。或直接在地址栏输入jupyter notebook
之后在界面右上角有new按键,点击python,即可创建python运行的环境。
运行每一单元格:快捷键Shift+Enter
-
在jupyter notebook此时的文件中,可以依次写下代码并运行,比如,写下一行代码后,可以点击上方运行按键直接运行,或者使用快捷键Ctrl+Enter。运行结束可以看到下方有对应的输出。
使用线性回归
张量的创建
- 逐行输入
python
import torch #导入torch
x = torch.arange(12) #创建
x #显示自动求导
python
import torch
x=torch.arange(4.0)
x.requires_grad_(True)
# 上面两行等价于:x = torch.arange(4.0,requires_grad=True)
y = 2* torch.dot(x,x)
y.backward()
x.grad
图像分类数据集Fashion-MNIST的下载
- 将数据集下载到内存中
python
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
d2l.use_svg_display()
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(root = "../data",train = True,transform = trans, download = True)
mnist_test = torchvision.datasets.FashionMNIST(root = "../data",train = False,transform = trans, download = True)
len(mnist_train),len(mnist_test)运行结果如下:

数据集保存在代码文件上一级的data文件夹中
小批量数据的可视化
python
#定义函数获取标签及可视化图像
def get_fashion_mnist_labels(labels):
text_labels = ['t-shirt','trouser','pullover','dress','coat','sandal','shirt','sneaker','bag','ankle boot']
return [text_labels[int(i)] for i in labels]
def show_images(imgs,num_rows,num_cols,titles = None, scale = 1.5):
figsize = (num_cols * scale,num_rows * scale)
_,axes = d2l.plt.subplots(num_rows,num_cols,figsize = figsize)
axes = axes.flatten()
for i,(ax,img) in enumerate(zip(axes,imgs)):
if torch.is_tensor(img):
ax.imshow(img.numpy())
else:
ax.imshow(img)
ax.axes.get_xaxis().set_visible(False)
ax.axes.get_yaxis().set_visible(False)
if titles:ax.set_title(titles[i])
return axes
#pytorch版本获取小批量数据集
X,y = next(iter(data.DataLoader(mnist_train,batch_size=18)))
show_images(X.reshape(18,28,28),2,9,titles = get_fashion_mnist_labels(y))运行结果,返回了训练集中的18张图片:
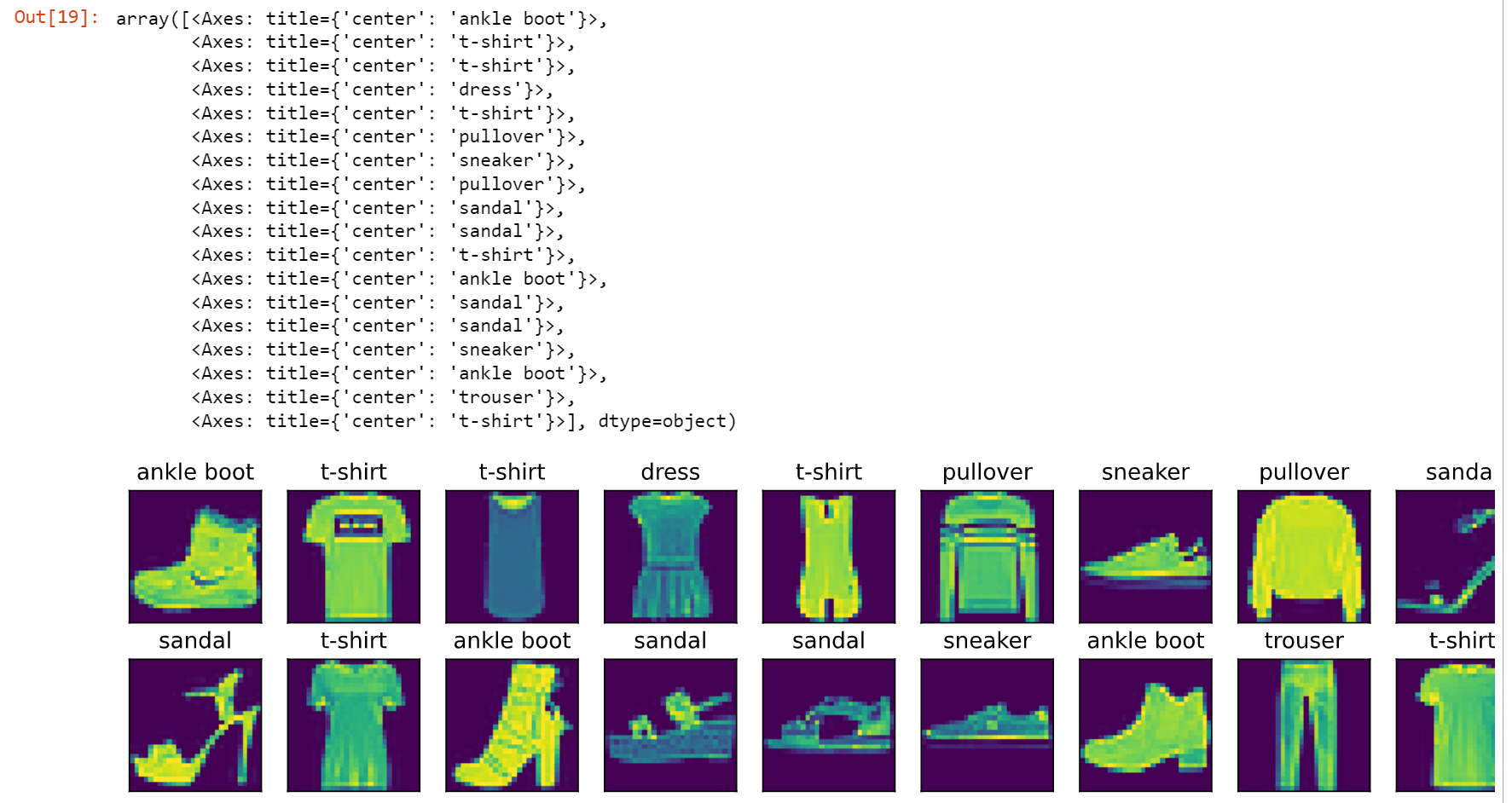
load_data_fashion_mnist函数
对该数据集的获取和下载,整合成完整函数如下,该函数在之后的模型训练中会使用:
python
def load_data_fashion_mnist(batch_size, resize=None):
trans = [transforms.ToTensor()]
if resize:
trans.insert(0, transforms.Resize(resize))
trans = transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(
root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
root="../data", train=False, transform=trans, download=True)
return (data.DataLoader(mnist_train, batch_size, shuffle=True,
num_workers=get_dataloader_workers()),
data.DataLoader(mnist_test, batch_size, shuffle=False,
num_workers=get_dataloader_workers()))权重衰退(处理过拟合)
权重衰退是常用的正则化技术之一。
引入超参数 λ \lambda λ,训练目标为:
m i n l ( w , b ) + λ 2 ∣ ∣ ω ∣ ∣ 2 min \ l(w,b)+\frac{\lambda}{2}||\omega||^2 min l(w,b)+2λ∣∣ω∣∣2
完整实现示例如下:
python
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05 #设置权重张量及偏置
train_data = d2l.synthetic_data(true_w, true_b, n_train) #使用人工合成的数据集
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)
#初始化参数
def init_params():
w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]
#定义惩罚
def l2_penalty(w):
return torch.sum(w.pow(2)) / 2
def train(lambd):
w, b = init_params()
net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss #定义线性回归模型和平方损失函数
num_epochs, lr = 100, 0.003
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
# 增加了L2范数惩罚项,
# 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
l = loss(net(X), y) + lambd * l2_penalty(w)
l.sum().backward()
d2l.sgd([w, b], lr, batch_size)
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数是:', torch.norm(w).item())
train(3)运行结果如下:
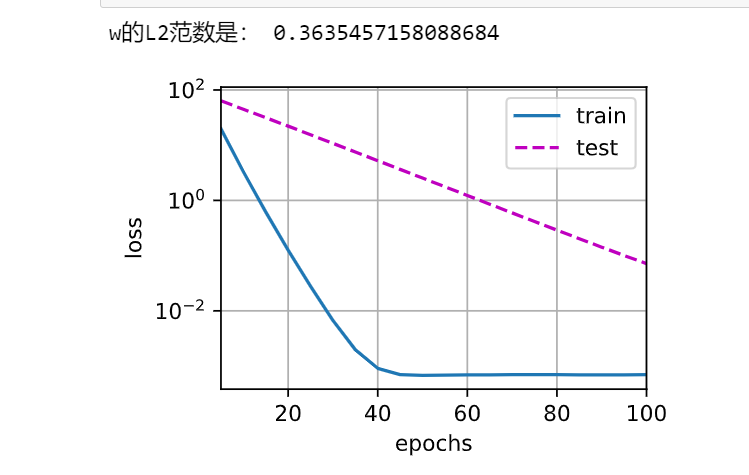
若进一步调大超参数,训练误差和测试误差相差的数量级会进一步降低。
层
卷积
超参数:
- 核的大小:卷积核,也即权重;
- 填充:在输入的周围添加额外的行/列,来控制输出形状的减少量;
- 步幅:每次滑动核窗口时的行/列的步长,可以成倍的减少输出形状;
- 输入和输出通道数
二维卷积实现:
python
import torch
from torch import nn
from d2l import torch as d2l
#二维卷积层
class Conv2D(nn.Module): #类/模块
def __init__(self,kernel_size): #初始化函数
super().__init__() #父类的初始化函数
self.weight = nn.Parameter(torch.rand(kernel_size)) #随机初始化权重
self.bias = nn.Parameter(torch.zeros(1)) #偏置参数(标量,初始为0)
def forward(self,x): #前向传播函数
return corr2d(x,self.weight)+self.bias池化
最大池化
平均池化
与卷积的不同:卷积可以实现多通道融合
池化层的作用:
- 缓解卷积层对位置的敏感性;
- 设置步幅stride,减少输出,即减少计算量,这一步也可以放在卷积层
- 数据本身会做增强/扰动,使得卷积层可以看到数据本身所做的变化,不会过拟合到数据的某一个位置,即淡化了池化层的作用
- 深度学习框架中的步幅与池化窗口的大小相同
- 通道数:仅由卷积层改变,每个卷积层的输出通道数等于该层使用的卷积核数量
- o u t p u t _ s i z e = f l o o r ( ( i n p u t _ s i z e − k e r n e l _ s i z e + 2 ∗ p a d d i n g ) / s t r i d e ) + 1 output\_size = floor((input\_size-kernel\_size+2*padding)/stride)+1 output_size=floor((input_size−kernel_size+2∗padding)/stride)+1
批量归一化
- 通过在每个小批量里加入噪音来控制模型复杂度。
- 固定小批量中的均值/随机偏移和方差/随机缩放,然后学习出适合的偏移和缩放。
- 可以加速收敛速度,但一般不改变模型精度。
直接调包使用:nn.BatchNorm2d/nn.BatchNorm1d/nn/BatchNorm3d
卷积神经网络
LeNet(卷积神经网络)实现
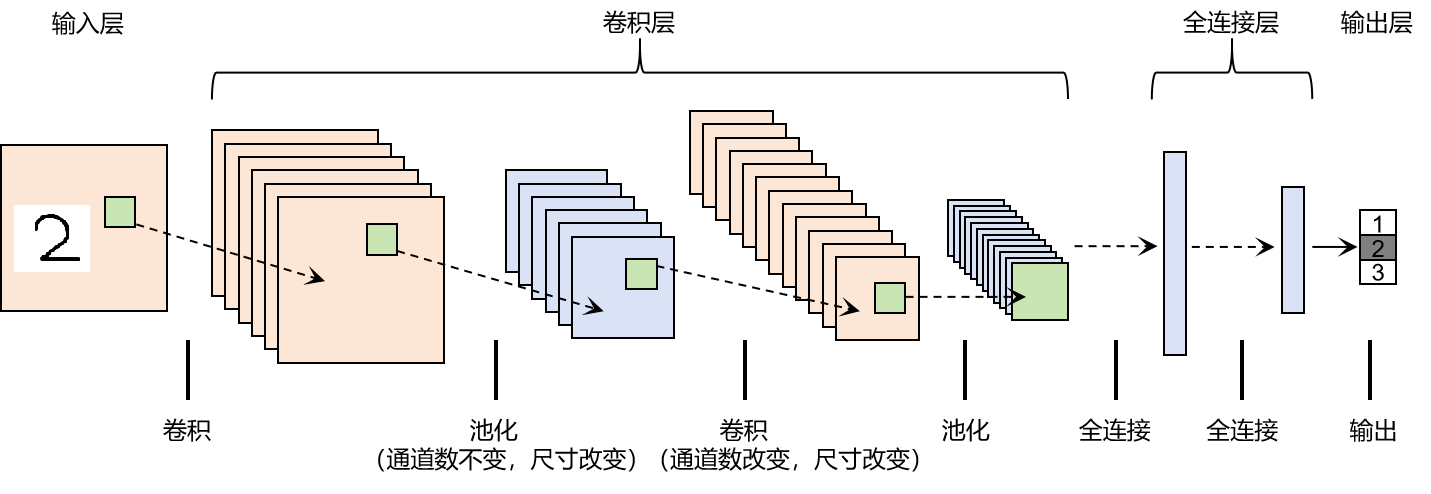
python
import torch
from torch import nn
from d2l import torch as d2l
class Reshape(torch.nn.Module):
def forward(self,x):
return x.view(-1,1,28,28) #输出(1,1,28,28)
net = torch.nn.Sequential(
Reshape(),nn.Conv2d(1,6,kernel_size = 5,padding = 2),nn.Sigmoid(), #输出(1,6,28,28)
nn.AvgPool2d(2,stride=2), #输出(1,6,14,14)
nn.Conv2d(6,16,kernel_size = 5),nn.Sigmoid(), #输出(1,6,10,10)
nn.AvgPool2d(2,stride = 2),nn.Flatten(), #输出(1,16,5,5),Flatten层输出(1,400)
nn.Linear(16*5*5,120),nn.Sigmoid(), #输出(1,120)
nn.Linear(120,84),nn.Sigmoid(), #输出(1,84)
nn.Linear(84,10)) #输出(1,10)
X = torch.rand(size=(1,1,28,28),dtype = torch.float32)
for layer in net:
X = layer(X)
print(layer.__class__.__name__,'output shape:\t',X.shape)AlexNet
与LeNet区别
| AlexNet | LeNet | |
|---|---|---|
| 激活函数 | Relu | Sigmoid |
| 池化层 | MaxPooling | AveragePooling |
| 其他 | 丢弃法、更大的池化窗口、更大的核窗口、更大的步长、数据增强 |
实现:
python
import torch
from torch import nn
from d2l import torch as d2l
net = nn.Sequential(
nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Flatten(),
nn.Linear(6400, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 10))VGG
- 改变设计思想,使模型更深更大。比如可以使用m个3*3卷积层和n个通道数。不同于Alexnet使用3个卷积层。
- VGG使用可重复使用的卷积块来构建深度卷积神经网络。
- 不同的卷积块个数和超参数可以得到不同复杂度的变种。
| VGG Block | NiN Block | GoogLeNet | |
|---|---|---|---|
| 内容 | m个3*3卷积+1个3*3最大池化层 | 1个卷积+2个当做全连接的1*1的卷积 | 5段,9个Inception块 |
Resnet
g ( x ) = x + f ( x ) g(x) = x+f(x) g(x)=x+f(x)
全称:residual net。
- 残差块包含Conv、Relu、BatchNorm及其重复;
- 使得很深的网络更加容易训练,甚至可以训练一千层的网络;
- 残差网络对随后的深层神经网络如卷积类网络/全连接层网络设计产生了深远影响。
下图为19层VGG、34层纯卷积网络、34层残差网络结构示意图:

相关基础概念及思想
- 深度学习的核心:在模型容量够大的前提下,通过各种手段控制模型容量,使得泛化误差降低。
- 通道数一般取 2 n 2^n 2n个,使得计算更为方便。
- 一般不改变现有模型,但可以稍微调整/降低 2 n 2^n 2n个通道数/拉宽拉窄输入输出