[优选算法专题二滑动窗口——长度最小的子数组]

题目链接

LeetCode长度最小的子数组

题目描述

题目详解

问题深度分析

首先明确问题需求：

• 输入：一个正整数数组nums和一个目标值target
• 输出：数组中和大于等于target的最短连续子数组的长度
• 特殊情况：如果没有这样的子数组，返回 0

这个问题的关键在于 "连续子数组" 和 "最短长度" 这两个约束条件。

算法选择理由

为什么选择滑动窗口（双指针）算法？

1. 暴力解法的局限性 ：

   暴力解法会检查所有可能的子数组，时间复杂度为 O (n²)，当数组长度很大时效率太低

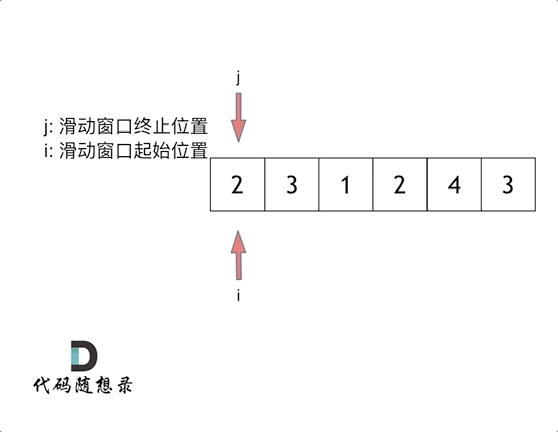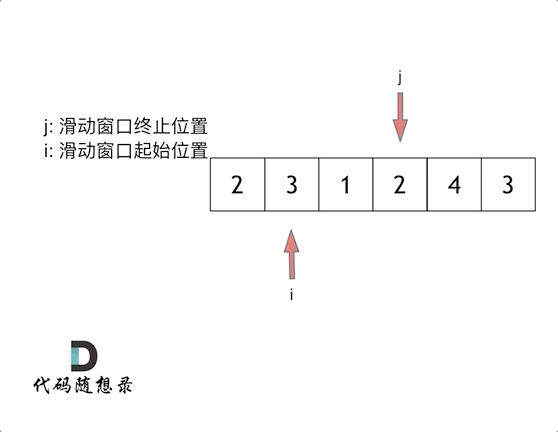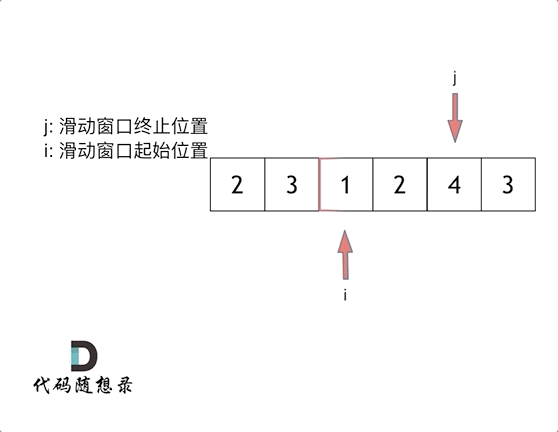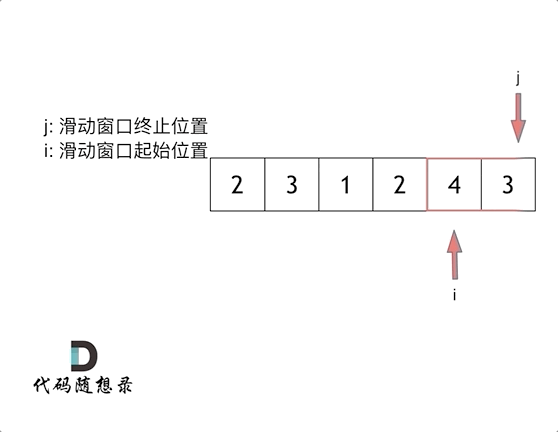
2. 滑动窗口的优势：

   • 利用数组中元素均为正整数的特性（这是关键！）
   • 当子数组和大于目标值时，扩大窗口
   • 当子数组和大于等于目标值时，缩小窗口
   • 每个元素最多被访问两次（一次右指针，一次左指针），时间复杂度 O (n)

关键代码细节解析

1. 初始化len = INT_MAX ：

   这是一个技巧，使用整数的最大值作为初始值，确保任何有效的子数组长度都会比它小，便于后续使用min()函数更新

2. 双指针的移动逻辑：

   • 外层 for 循环控制右指针right，负责扩大窗口
   • 内层 while 循环控制左指针left，负责在满足条件时缩小窗口

3.窗口调整的核心逻辑：

while(sum >= target) {
    len = min(len, right-left+1);  // 更新最小长度
    sum -= nums[left++];           // 缩小窗口
}

当窗口内元素和满足条件时，我们尝试通过移动左指针来找到更短的有效子数组

4.最终返回值处理：

return len == INT_MAX ? 0 : len;

完整代码：

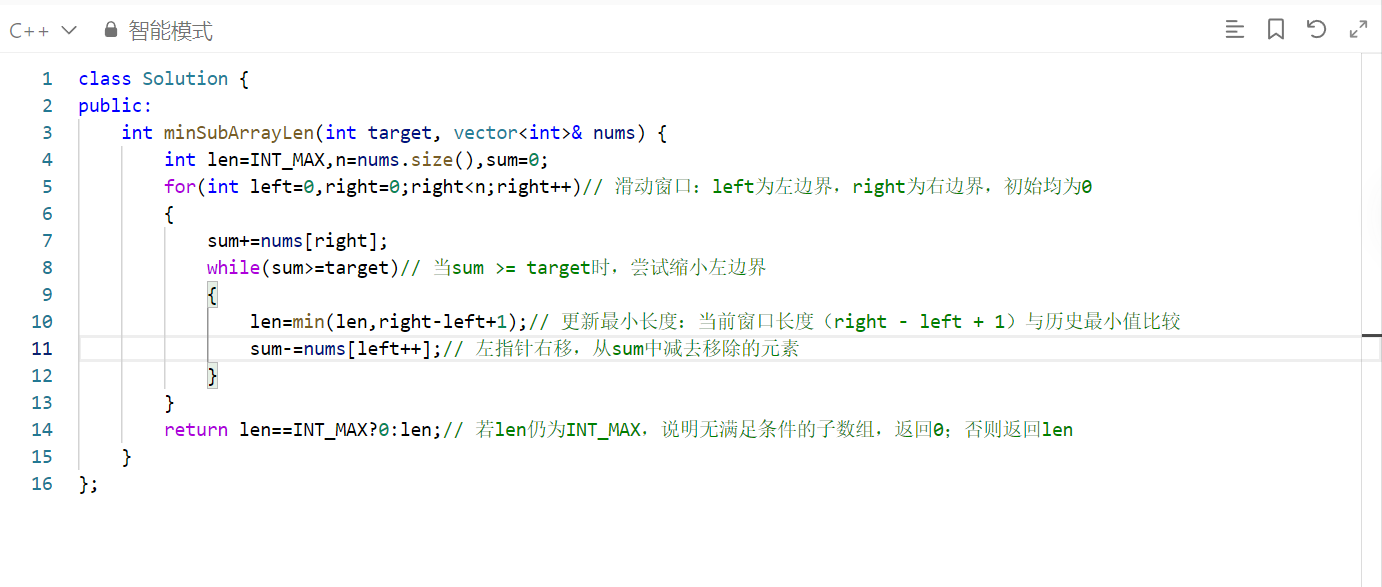
边界情况处理

1. 数组为空 ：nums.size() == 0，此时直接返回 0
2. 单个元素：如果该元素大于等于 target，返回 1；否则返回 0
3. 所有元素之和仍小于 target：返回 0
4. 刚好有一个元素等于 target：返回 1

这种滑动窗口的解法充分利用了数组元素为正整数的特性，是解决该问题的最优方案，时间复杂度 O (n)，空间复杂度 O (1)，在处理大规模数据时表现出色。