最小路径和 - 技术栈

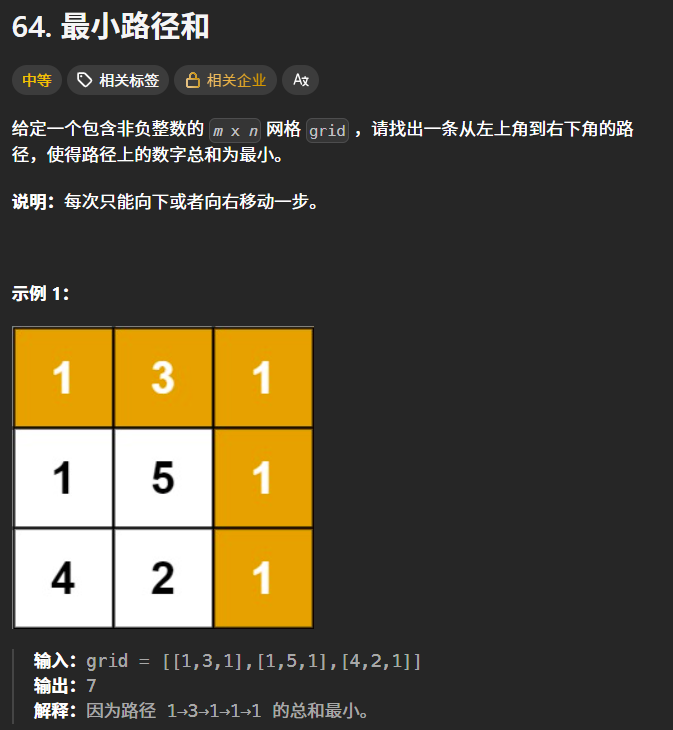
dp问题描述

最小路径和

确定本题的状态表示

dp[i][j]表示的是矩阵从左上角走到(i,j)位置一路上的数字总和的最小值

确定本题的状态转移方程

本题的状态转移方程依然是
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];

但是要注意边界条件，因为边界值初始化为0，我们比的又是最小值，所以当i和j位于矩阵数值边界时，不能把最外围那层0加进来比，否则会污染有效数据

填表求值

根据初始条件和状态转移方程，确定填表顺序，进而逐步填满dp表，最终返回题目要的结果

代码实现

复制代码

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m=grid.size();
        if(m==0) return 0;
        int n=grid[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,0));
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(i==1)
                    dp[i][j]=dp[i][j-1]+grid[i-1][j-1];
                else if(j==1)
                    dp[i][j]=dp[i-1][j]+grid[i-1][j-1];
                else
                    dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
                cout << "dp["<<i<<"]["<<j<<"]="<< dp[i][j]<< endl;
            }
        }
        return dp[m][n];
    }
};