数据结构与算法：线段树（一）：基本原理

WBluuue2025-08-18 11:43

前言

这玩意儿太妙了......

一、应用场景

首先，线段树可以维护的信息要求为，父范围上的信息可以在O(1)的时间里，由子范围的信息加工得到。举个例子，假如知道了左侧和右侧的累加和，那么只要相加就可以在O(1)的时间里得到整体的累加和。类似的，假如知道了左侧和右侧的最大值，那么只要比较一下也能在O(1)的时间里得到整体的最大值。

线段树的经典功能就是范围查询和范围修改，其中范围修改还支持重置一个范围上的所有数，单次调用的时间复杂度为O(logn)。而如果范围修改功能想要做到O(logn)，那么就必须保证当在某个范围上统一进行了某种修改操作，可以用O(1)的时间把这个范围上要维护的信息加工出来。举个例子，假如某个范围上的累加和为100，那么当这个范围上的数统一加了5后，那修改后的累加和就是100直接加上5乘以范围内的数字个数即可，所以就可以在O(1)的时间里加工出来。

二、组织信息的方式

1.经典结构

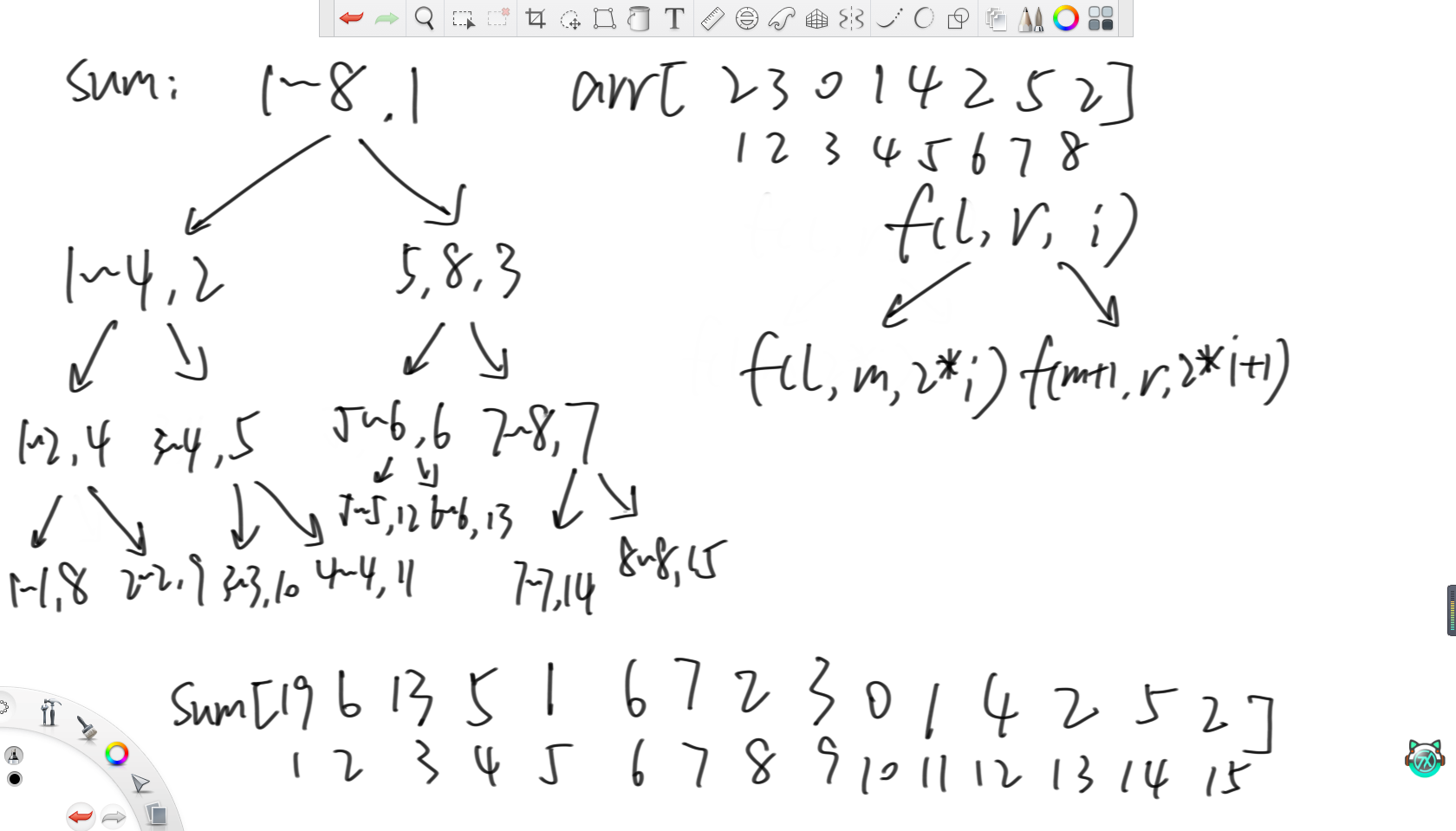
线段树其实是一种二叉树，其原理就是设置一个sum数组存区间累加和。之后，从原数组的整个单位开始递归，每次取当前区间的中点，然后分别去构建左右孩子。其中，如果当前区间的累加和存在sum数组的i位置，那么左孩子的区间就存在2i位置，右孩子存在2i+1位置。以上图为例，原数组长度为8，那么在建树时首先调用（1，8，1），表示原数组1～8范围的累加和存在sum数组的1位置。之后，去调左孩子（1，4，2）和右孩子（5，8，3），表示原数组1～4范围的累加和存在sum数组的2位置，5～8范围的累加和存在sum数组的3位置。之后以此类推往下调递归，当l＝r时，说明只有一个数了，那么就直接等于原数组的值即可。在返回时，只需要根据左孩子和右孩子在sum里的对应下标，相加就能得到当前范围的sum值。

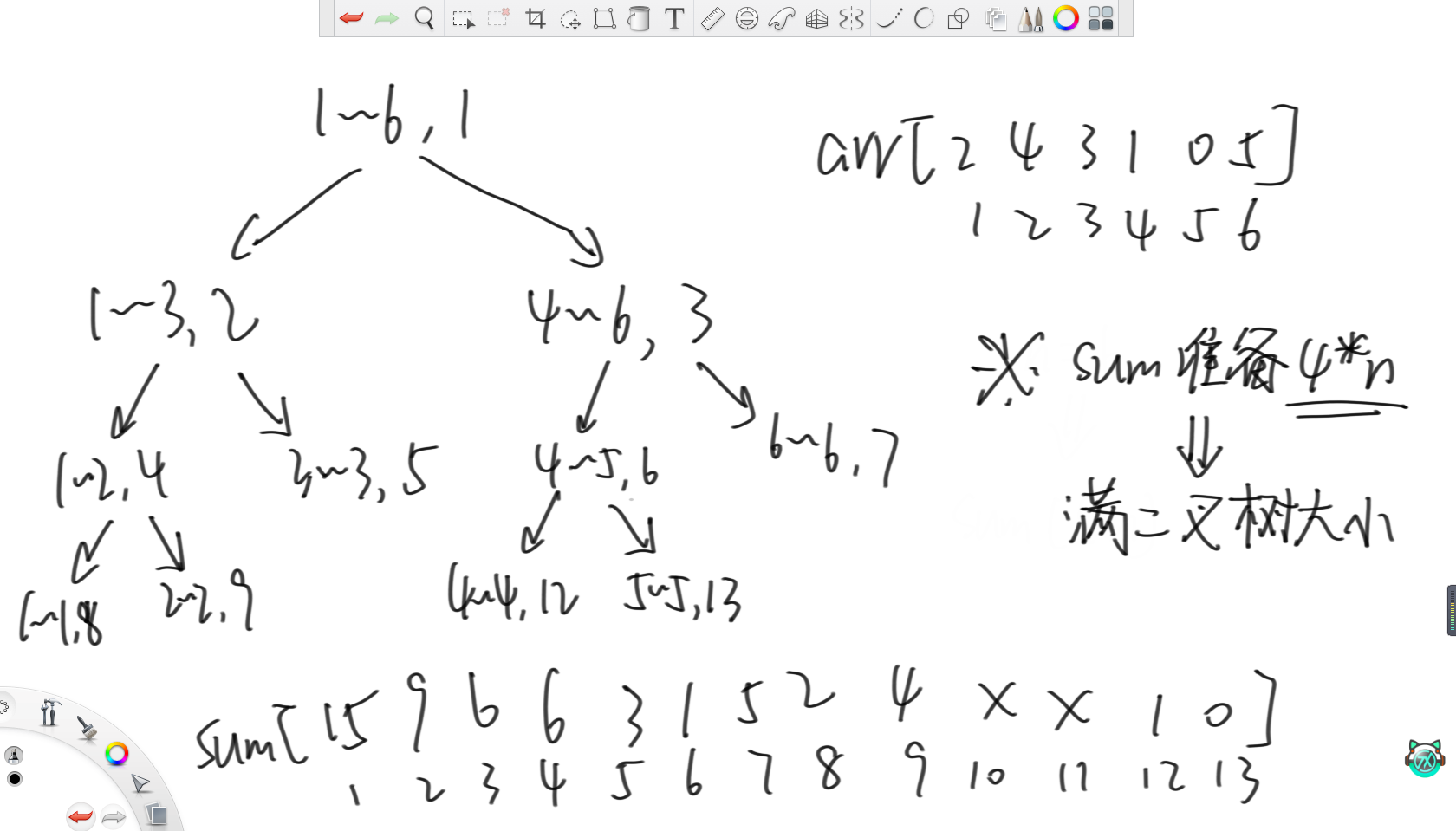
在上面的例子里，原数组长度为8，是2的幂。那么对于长度不是2的幂的数组，那么这棵二叉树就不是满二叉树。在之前的例子里，长度为8的数组要开15长度的sum数组。而在上图例子中，原数组长度为6，那么sum只要开到13长度即可，而且中间10和11位置没有用。

进一步观察可以发现，整个二叉树最多最多就是当原数组长度为2的幂时，此时整个二叉树为满二叉树。根据满二叉树的节点个数等于2的树高次方再减一，而树高又等于以2为底长度n的对数向上取整。所以代入化简一下就能发现，sum数组准备四倍的长度大小就完全够用了。

2.范围查询

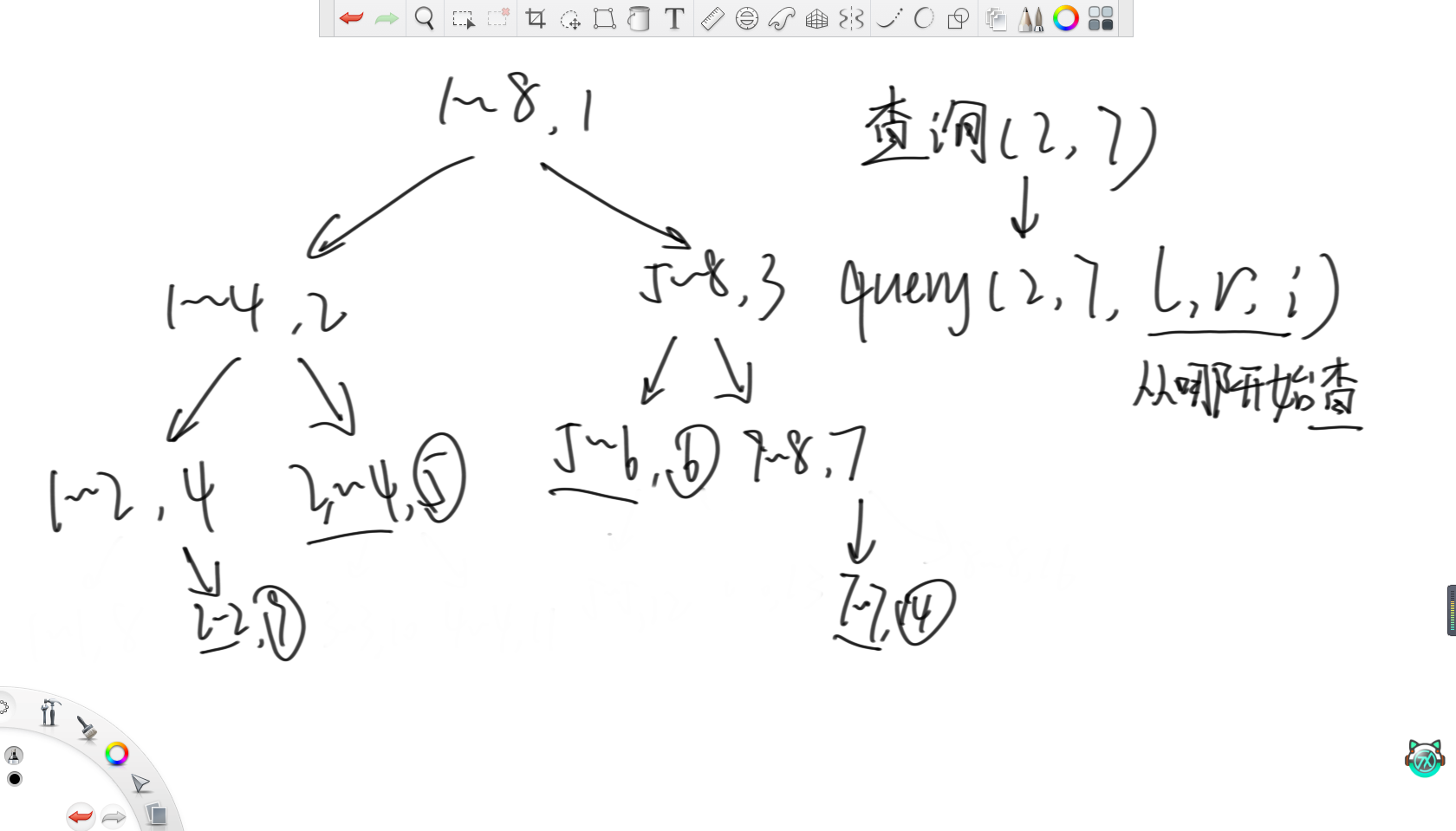
对于要查询的范围[jobl,jobr]，在递归时一直带着这两个参数，同时还设置（l，r，i），同样表示当前来到的节点所负责的范围和在sum数组里对应的位置。之后，如果当前范围被要查询的范围完全包住，就直接返回当前范围的sum[i]。如果当前范围没被完全包住，且孩子节点是部分被要查询的范围包住，就去这个孩子节点调递归即可。

举个例子，假如要查询[2,7]上的累加和，那么依然是从（1，8，1）开始调。因为没被查询区间全包，且左右孩子的范围里都有要查询的，那么就去调左右孩子。同理，由于没有全被包，所以继续调左右孩子。之后，由于区间（3，4）和（5，6）被完全包住了，那就直接返回在sum里的累加和即可。直到递归调用到（2，2）和（7，7），同样由于被全包了，也直接返回即可。

3.范围修改------懒更新

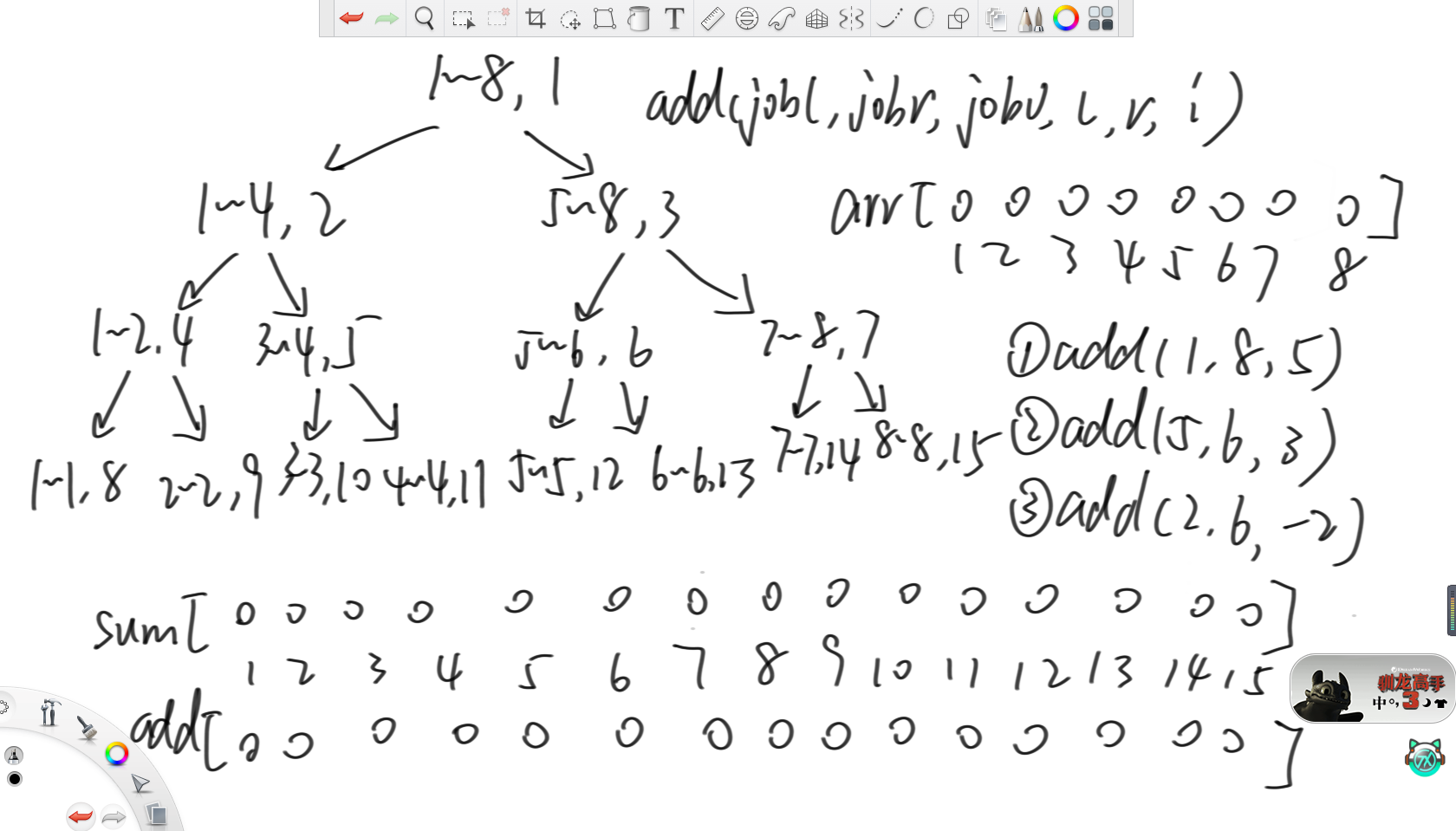
线段树范围修改的方法就非常妙了。

这个方法称为"懒更新"，其过程和我的世界里的区块加载类似。在我的世界中，游戏只加载玩家周围的区块，离玩家远的区块是不加载的。所以，懒更新的核心思想就是，对当前查询没用的信息，先存着不在sum数组里更新，等到真的有一条查询要用的时候再去更新。实现方法就是，额外建立一个和sum等长的add数组，存sum数组里每个位置应该增加的信息。

以上图为例，现在有三条增加操作，分别在(1,8)范围上加5，在(5,6)范围上加3和在(2,6)范围上减2，即加-2。

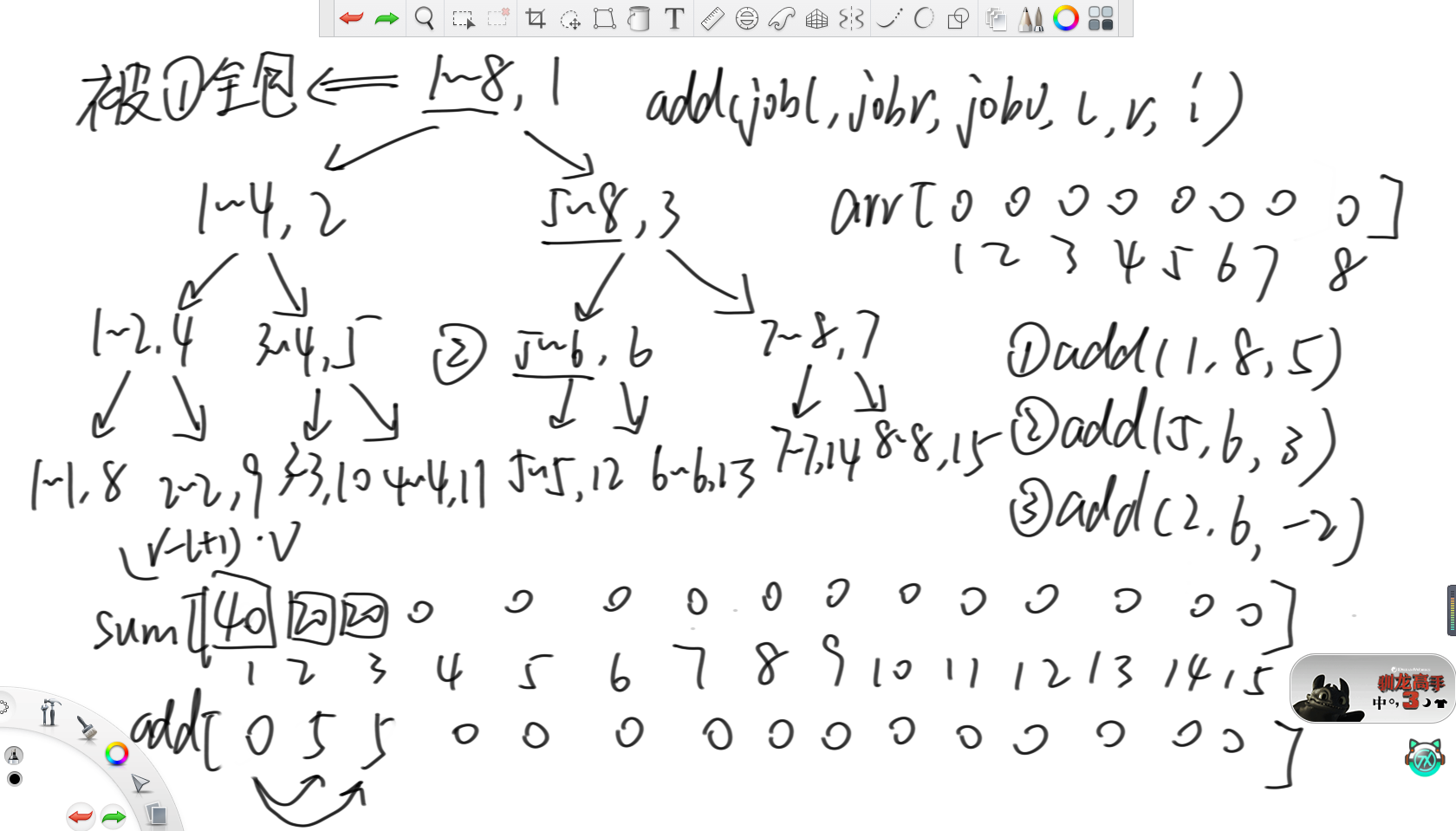
首先，对于(1,8)范围增加5的命令，就从(1,8,1)开始调递归。此时可以发现，在来到(1,8,1)时，此时的区间(1,8)被命令区间(1,8)全包了，那么就直接去sum数组和add数组里设置。具体设置方法是，将add[i]位置设置为要增加的数，所以add[1]就被设置为5，将增加信息"懒"在这里先不下发。而因为sum[i]的含义为当前区间内的累加和，所以就需要设置为当前区间内的数字个数乘以要增加的数，所以sum[1]就被设置为8乘以5等于40。

之后，对于(5,6)范围上增加3的命令，同样从头开始调递归。此时因为当前add数组里有数，即存在懒信息，又因为当前区间没有被全包，那么就需要把懒信息往下发，然后去左右孩子调递归。下发的方法就是分别去设置左右孩子的懒信息，所以就将add[2]和add[3]都设置为5，然后再把sum[2]和sum[3]设置为4乘以5等于20。最后，因为1位置的懒信息已经下发了，所以就把add[1]清空为0。

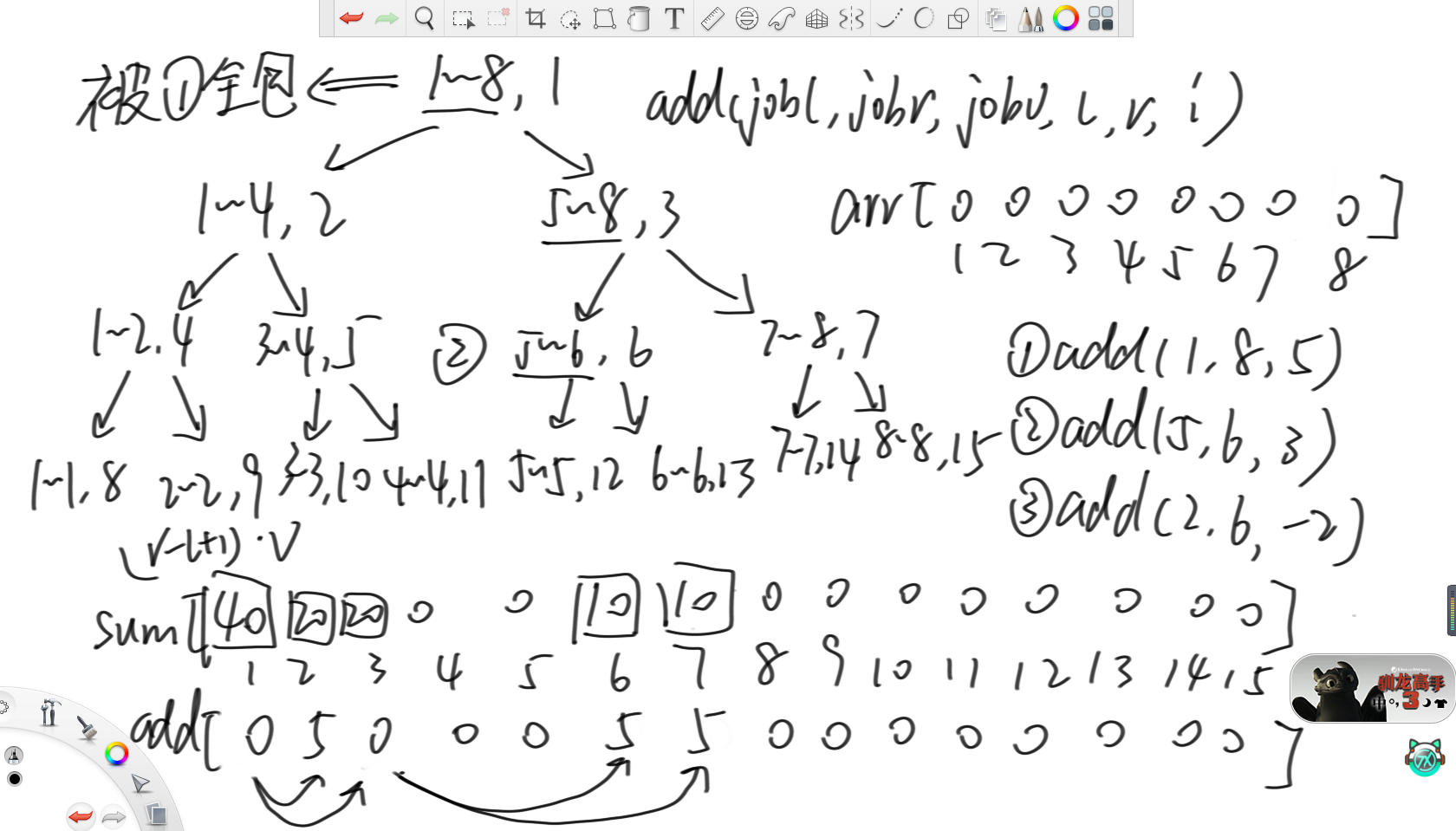
之后，因为左孩子(1,4)范围上没有命令区间的数，那就不去左孩子。而因为右孩子(5,8)范围上有命令区间内的数，所以去右孩子。在来到右孩子时，因为(5,8)没有被命令区间(5,6)全包，所以需要继续调递归，那么就需要继续往下发懒信息，方法同上。

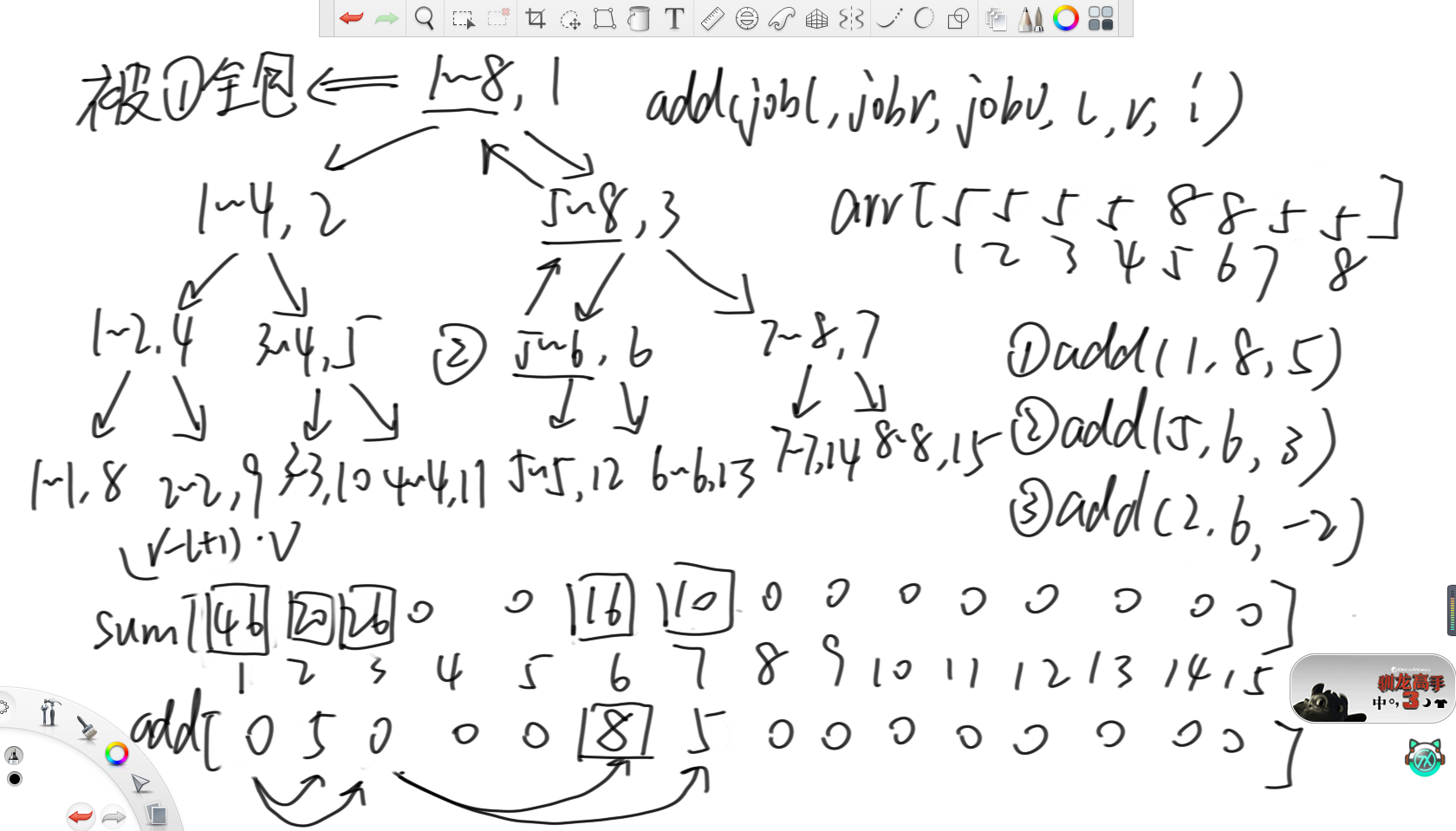
此时发现左孩子(5,6)范围上有命令区间的数，那么就去左孩子调递归。此时，因为当前范围(5,6)被命令区间全包，所以就直接去sum和add数组里设置。因为当前命令是增加3，所以add[6]就要加上3变成8，sum[6]就要加上2乘以3等于6，变成16。

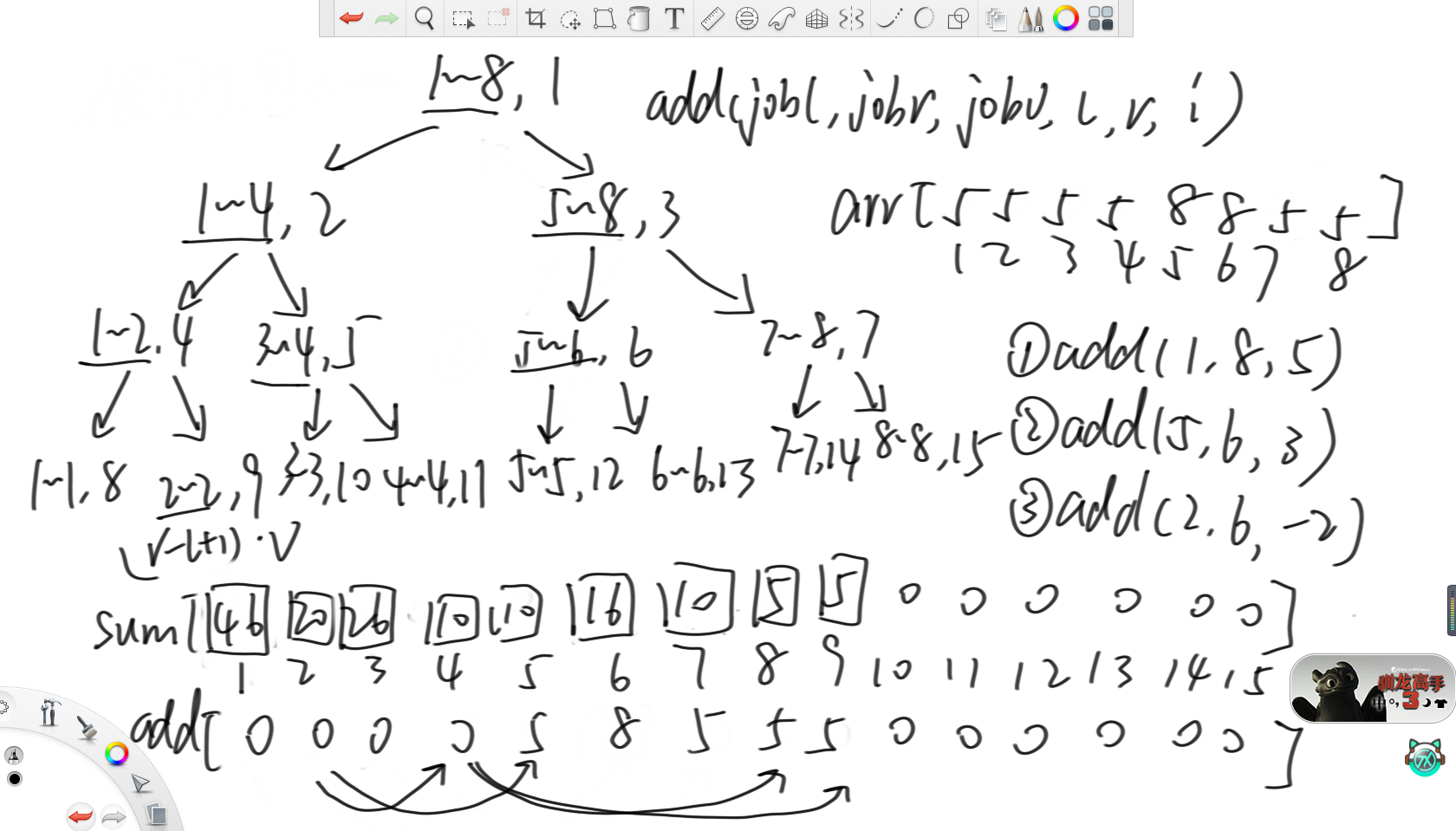
对于第三个命令，就比较复杂了。还是重复上述过程，当来到(1,4,2)时，因为没被全包，所以先下发懒信息，然后去左右孩子调递归。之后，因为(1,2,4)也没被全包，所以需要再下发懒信息，之后去右孩子调递归。同理(5,6)范围也是如此。

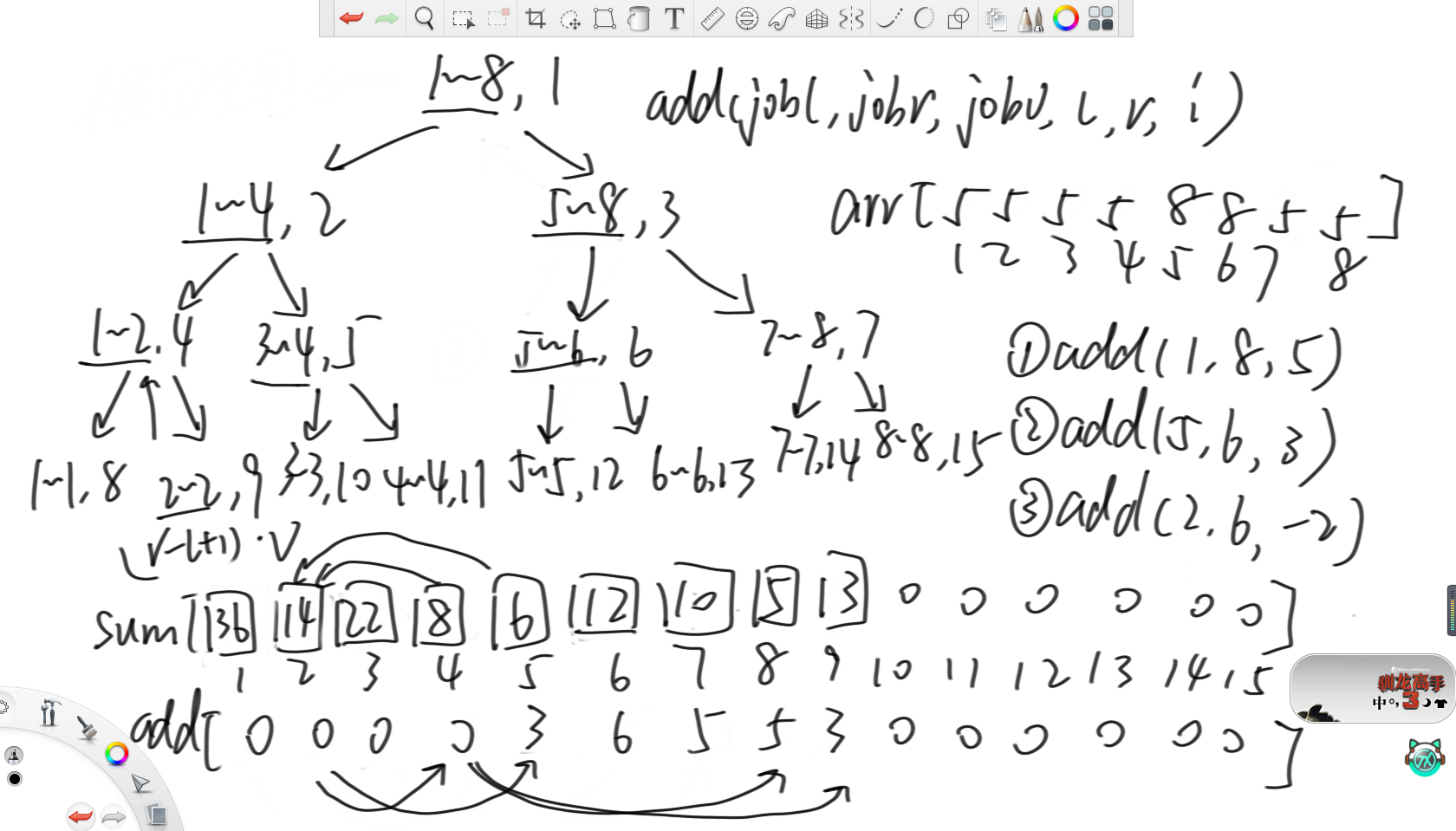
此时因为(2,2)被全包了，所以就更新sum[9]和add[9]。之后在返回时，因为孩子节点的sum发生了变化，所以还要把父亲节点的sum更新对，那么就是将sum[4]更新成左右孩子的sum之和，所以sum[4]就等于5加上3等于8。之后，因为sum[4]发生了变化，所以要继续往上更新，所以sum[2]就需要更新成8加上6等于14。此外，在(5,6)范围更新后，还需要将sum[3]更新为12加上10等于22。最后，需要将sum[1]更新为14加上22即可。

三、例题

1.线段树 1

之前还不理解群友为啥要准备模版，现在发现这个代码量和代码复杂度如果不准备模版的话光是抄就得抄上个几分钟......

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;

const int MAXN=1e5+5;

vector<ll>arr(MAXN);

//开4倍空间
//累加和数组
vector<ll>sum(MAXN<<2);
//懒信息数组
vector<ll>info(MAXN<<2);

//更新懒信息和累加和
void lazy(int i,ll v,int n)
{
    sum[i]+=v*n;
    info[i]+=v;
}

//累加和信息汇总
void up(int i)
{
    //父范围累加和=左范围累加和+右范围累加和
    sum[i]=sum[i<<1]+sum[i<<1|1];
}

//懒信息下发
//ln:左范围个数 rn:右范围个数
void down(int i,int ln,int rn)
{
    //有懒信息
    if(info[i]!=0)
    {
        //往左范围发
        lazy(i<<1,info[i],ln);
        //往右范围发
        lazy(i<<1|1,info[i],rn);
        //父范围懒信息归零
        info[i]=0;
    }
}

//构建
void build(int l,int r,int i)
{
    if(l==r)//叶节点
    {
        sum[i]=arr[l];
    }
    else
    {
        int m=(l+r)>>1;

        //左范围
        build(l,m,i<<1);
        //右范围
        build(m+1,r,i<<1|1);

        //统计累加和
        up(i);
    }
    //初始没有懒信息
    info[i]=0;
}

//范围增加
void add(int jobl,int jobr,ll jobv,int l,int r,int i)
{
    if(jobl<=l&&r<=jobr)//被全包了
    {
        //直接更新
        lazy(i,jobv,r-l+1);
    }
    else
    {
        int m=(l+r)>>1;

        //下发懒信息
        down(i,m-l+1,r-m);

        //需要去左范围
        if(jobl<=m)
        {   
            add(jobl,jobr,jobv,l,m,i<<1);
        }
        //需要去右范围
        if(m+1<=jobr)
        {
            add(jobl,jobr,jobv,m+1,r,i<<1|1);
        }

        //汇总
        up(i);
    }
}

//范围查询
ll query(int jobl,int jobr,int l,int r,int i)
{
    //被全包了
    if(jobl<=l&&r<=jobr)
    {
        return sum[i];
    }

    //没被全包，需要往下扎
    int m=(l+r)>>1;

    //下发懒信息
    down(i,m-l+1,r-m);
    
    ll ans=0;
    //需要去左范围
    if(jobl<=m)
    {
        ans+=query(jobl,jobr,l,m,i<<1);
    }
    //需要去右范围
    if(m+1<=jobr)
    {
        ans+=query(jobl,jobr,m+1,r,i<<1|1);
    }
    return ans;
}

void solve()
{
    int n,q;
    cin>>n>>q;
    for(int i=1;i<=n;i++)
    {
        cin>>arr[i];
    }

    build(1,n,1);

    while(q--)
    {
        int type;
        cin>>type;

        if(type==1)
        {
            int x,y;
            ll k;
            cin>>x>>y>>k;

            add(x,y,k,1,n,1);
        }
        else
        {
            int x,y;
            cin>>x>>y;

            cout<<query(x,y,1,n,1)<<endl;
        }
    }
}

int main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--)
    {
        solve();    
    }
    return 0;
}

这里，info就是上述的add数组，负责存住懒信息。lazy就是懒更新的函数，所以需要接受三个参数，分别是更新的位置i，要更新的数v和范围的大小n。那么每次更新时都需要让sum[i]加上v乘以n，add[i]加上v即可。之后，up就是向上汇总孩子信息的函数，需要接受更新的父节点位置i，然后父节点的sum直接等于左右孩子的sum即可。down就是下发懒信息的函数，所以只要当前节点的add数组不为0，即有信息需要下发，那么就分别去左右孩子调lazy方法，然后将当前的add[i]设置为0即可。

之后，add就是范围增加函数，所以只要当前范围没被全包，就先调用down方法下发懒信息。之后如果左孩子有数就去左孩子调递归，右孩子有数就去右孩子调递归。都修改完以后再调用up方法汇总信息。query就是范围查询函数，如果当前范围被全包了，就直接返回sum[i]即可。否则就先下发懒信息，然后同样左边有就调左边，右边有就调右边。

如果只要求单点增加的话，那根本就不需要懒更新了，每次增加直接扎更新到底就行了。

2.线段树的范围重置

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;

const int MAXN=1e5+5;

vector<ll>arr(MAXN);

//开4倍空间
//累加和数组
vector<ll>sum(MAXN<<2);
//懒信息数组 -> 改成什么数
vector<ll>info(MAXN<<2);
//重置任务是否没往下发
vector<bool>update(MAXN<<2);

//更新懒信息和累加和
void lazy(int i,ll v,int n)
{
    //全改
    sum[i]=v*n;
    info[i]=v;
    //更新过了，但还没往下发
    update[i]=true;
}

//累加和信息汇总
void up(int i)
{
    //父范围累加和=左范围累加和+右范围累加和
    sum[i]=sum[i<<1]+sum[i<<1|1];
}

//懒信息下发
//ln:左范围个数 rn:右范围个数
void down(int i,int ln,int rn)
{
    //没往下发
    if(update[i])
    {
        //往左范围发
        lazy(i<<1,info[i],ln);
        //往右范围发
        lazy(i<<1|1,info[i],rn);
        //更新结束，修改状态
        update[i]=false;
    }
}

//构建
void build(int l,int r,int i)
{
    if(l==r)//叶节点
    {
        sum[i]=arr[l];
    }
    else
    {
        int m=(l+r)>>1;

        //左范围
        build(l,m,i<<1);
        //右范围
        build(m+1,r,i<<1|1);

        //统计累加和
        up(i);
    }
    //初始没有懒信息，也不需要往下发
    info[i]=0;
    update[i]=false;
}

//范围重置
void change(int jobl,int jobr,ll jobv,int l,int r,int i)
{
    if(jobl<=l&&r<=jobr)//被全包了
    {
        //直接更新
        lazy(i,jobv,r-l+1);
    }
    else
    {
        int m=(l+r)>>1;

        //下发懒信息
        down(i,m-l+1,r-m);

        //需要去左范围
        if(jobl<=m)
        {   
            change(jobl,jobr,jobv,l,m,i<<1);
        }
        //需要去右范围
        if(m+1<=jobr)
        {
            change(jobl,jobr,jobv,m+1,r,i<<1|1);
        }

        //汇总
        up(i);
    }
}

//范围查询
ll query(int jobl,int jobr,int l,int r,int i)
{
    //被全包了
    if(jobl<=l&&r<=jobr)
    {
        return sum[i];
    }

    //没被全包，需要往下扎
    int m=(l+r)>>1;

    //下发懒信息
    down(i,m-l+1,r-m);
    
    ll ans=0;
    //需要去左范围
    if(jobl<=m)
    {
        ans+=query(jobl,jobr,l,m,i<<1);
    }
    //需要去右范围
    if(m+1<=jobr)
    {
        ans+=query(jobl,jobr,m+1,r,i<<1|1);
    }
    return ans;
}

void randomArray(int n,int v)
{
    for(int i=1;i<=n;i++)
    {
        arr[i]=rand()%v;
    }
}

void checkUpdate(int jobl,int jobr,ll jobv,vector<ll>&check)
{
    for(int i=jobl;i<=jobr;i++)
    {
        check[i]=jobv;
    }
}

ll checkQuery(int jobl,int jobr,vector<ll>&check)
{
    ll ans=0;
    for(int i=jobl;i<=jobr;i++)
    {
        ans+=check[i];
    }
    return ans;
}

void solve()
{
    srand(time(0));

    int N=1000;
    int V=2000;
    int T=5000000;
    
    randomArray(N,V);

    //建立
    build(1,N,1);

    //生成验证结构
    vector<ll>check(N+1);
    for(int i=1;i<=N;i++)
    {
        check[i]=arr[i];
    }

    cout<<"Start"<<endl;
    for(int i=1;i<=T;i++)
    {
        int op=rand()%2;

        //随机加标
        int x=rand()%N+1;
        int y=rand()%N+1;

        int jobl=min(x,y);
        int jobr=max(x,y);

        if(op==0)//更新
        {
            int jobv=rand()%(V*2)-V;
            change(jobl,jobr,jobv,1,N,1);
            checkUpdate(jobl,jobr,jobv,check);
        }
        else//查询
        {
            ll ans1=query(jobl,jobr,1,N,1);
            ll ans2=checkQuery(jobl,jobr,check);

            if(ans1!=ans2)
            {
                cout<<"Wrong"<<endl;
            }
        }
    }
    cout<<"Over"<<endl;
}

int main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--)
    {
        solve();    
    }
    return 0;
}

懂了上面的整体流程后，这个就很好想了。因为是整个范围上都重置，所以lazy直接每次把info和sum设置成要改的数v即可。这里需要注意，由于info[i]等于0无法判断是没有懒信息还是重置成0，所以还要准备一个update数组，存当前的info信息是否没被下发，所以每次lazy还要将当前i的update改成true，表示懒信息更新了，还没下发。所以down函数里就改成判断update是否为true，即还没下发，下发完将update改成false即可。

3.线段树维护最大值

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;

const int MAXN=1e5+5;

vector<ll>arr(MAXN);

//开4倍空间
//最大值数组
vector<ll>mx(MAXN<<2);
//懒信息数组
vector<ll>info(MAXN<<2);

//更新懒信息和累加和
void lazy(int i,ll v)
{
    //直接改 -> 所有数字都增加，最大值只增加一份
    mx[i]+=v;
    info[i]+=v;
}

//最大值信息汇总
void up(int i)
{
    //对比
    mx[i]=max(mx[i<<1],mx[i<<1|1]);
}

//懒信息下发
void down(int i)
{
    //没往下发
    if(info[i]!=0)
    {
        //往左范围发
        lazy(i<<1,info[i]);
        //往右范围发
        lazy(i<<1|1,info[i]);
        info[i]=0;
    }
}

//构建
void build(int l,int r,int i)
{
    if(l==r)//叶节点
    {
        mx[i]=arr[l];
    }
    else
    {
        int m=(l+r)>>1;

        //左范围
        build(l,m,i<<1);
        //右范围
        build(m+1,r,i<<1|1);

        //统计
        up(i);
    }
    //初始没有懒信息
    info[i]=0;
}

//范围增加
void add(int jobl,int jobr,ll jobv,int l,int r,int i)
{
    if(jobl<=l&&r<=jobr)//被全包了
    {
        //直接更新
        lazy(i,jobv);
    }
    else
    {
        int m=(l+r)>>1;

        //下发懒信息
        down(i);

        //需要去左范围
        if(jobl<=m)
        {   
            add(jobl,jobr,jobv,l,m,i<<1);
        }
        //需要去右范围
        if(m+1<=jobr)
        {
            add(jobl,jobr,jobv,m+1,r,i<<1|1);
        }

        //汇总
        up(i);
    }
}

//范围查询
ll query(int jobl,int jobr,int l,int r,int i)
{
    //被全包了
    if(jobl<=l&&r<=jobr)
    {
        return mx[i];
    }

    //没被全包，需要往下扎
    int m=(l+r)>>1;

    //下发懒信息
    down(i);
    
    ll ans=-1e9;
    //需要去左范围
    if(jobl<=m)
    {
        ans=max(ans,query(jobl,jobr,l,m,i<<1));
    }
    //需要去右范围
    if(m+1<=jobr)
    {
        ans=max(ans,query(jobl,jobr,m+1,r,i<<1|1));
    }
    return ans;
}

void randomArray(int n,int v)
{
    for(int i=1;i<=n;i++)
    {
        arr[i]=rand()%v;
    }
}

void checkUpdate(int jobl,int jobr,ll jobv,vector<ll>&check)
{
    for(int i=jobl;i<=jobr;i++)
    {
        check[i]+=jobv;
    }
}

ll checkQuery(int jobl,int jobr,vector<ll>&check)
{
    ll ans=-1e9;
    for(int i=jobl;i<=jobr;i++)
    {
        ans=max(ans,check[i]);
    }
    return ans;
}

void solve()
{
    srand(time(0));

    int N=1000;
    int V=2000;
    int T=5000000;
    
    randomArray(N,V);

    //建立
    build(1,N,1);

    //生成验证结构
    vector<ll>check(N+1);
    for(int i=1;i<=N;i++)
    {
        check[i]=arr[i];
    }

    cout<<"Start"<<endl;
    for(int i=1;i<=T;i++)
    {
        int op=rand()%2;

        //随机加标
        int x=rand()%N+1;
        int y=rand()%N+1;

        int jobl=min(x,y);
        int jobr=max(x,y);

        if(op==0)//更新
        {
            int jobv=rand()%(V*2)-V;
            add(jobl,jobr,jobv,1,N,1);
            checkUpdate(jobl,jobr,jobv,check);
        }
        else//查询
        {
            ll ans1=query(jobl,jobr,1,N,1);
            ll ans2=checkQuery(jobl,jobr,check);

            if(ans1!=ans2)
            {
                cout<<"Wrong"<<endl;
            }
        }
    }
    cout<<"Over"<<endl;
}

int main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--)
    {
        solve();    
    }
    return 0;
}

最大值的也好理解，就是在lazy里每次把最大值数组mx加上v即可，因为整个区间增加后的最大值就是之前的最大值增加。之后query和up函数改成判断最大值即可。

4.范围重置且维护最大值

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;

const int MAXN=1e5+5;

vector<ll>arr(MAXN);

//开4倍空间
//最大值数组
vector<ll>mx(MAXN<<2);
//懒信息数组 -> 改成什么数
vector<ll>info(MAXN<<2);
//重置任务是否没往下发
vector<bool>update(MAXN<<2);

//更新懒信息和最大值
void lazy(int i,ll v)
{
    //直接改
    mx[i]=v;
    info[i]=v;
    //更新过了，但还没往下发
    update[i]=true;
}

//最大值信息汇总
void up(int i)
{
    mx[i]=max(mx[i<<1],mx[i<<1|1]);
}

//懒信息下发
void down(int i)
{
    //没往下发
    if(update[i])
    {
        //往左范围发
        lazy(i<<1,info[i]);
        //往右范围发
        lazy(i<<1|1,info[i]);
        //更新结束，修改状态
        update[i]=false;
    }
}

//构建
void build(int l,int r,int i)
{
    if(l==r)//叶节点
    {
        mx[i]=arr[l];
    }
    else
    {
        int m=(l+r)>>1;

        //左范围
        build(l,m,i<<1);
        //右范围
        build(m+1,r,i<<1|1);

        //统计最大值
        up(i);
    }
    //初始没有懒信息，也不需要往下发
    info[i]=0;
    update[i]=false;
}

//范围重置
void change(int jobl,int jobr,ll jobv,int l,int r,int i)
{
    if(jobl<=l&&r<=jobr)//被全包了
    {
        //直接更新
        lazy(i,jobv);
    }
    else
    {
        int m=(l+r)>>1;

        //下发懒信息
        down(i);

        //需要去左范围
        if(jobl<=m)
        {   
            change(jobl,jobr,jobv,l,m,i<<1);
        }
        //需要去右范围
        if(m+1<=jobr)
        {
            change(jobl,jobr,jobv,m+1,r,i<<1|1);
        }

        //汇总
        up(i);
    }
}

//范围查询
ll query(int jobl,int jobr,int l,int r,int i)
{
    //被全包了
    if(jobl<=l&&r<=jobr)
    {
        return mx[i];
    }

    //没被全包，需要往下扎
    int m=(l+r)>>1;

    //下发懒信息
    down(i);
    
    ll ans=-1e9;
    //需要去左范围
    if(jobl<=m)
    {
        ans=max(ans,query(jobl,jobr,l,m,i<<1));
    }
    //需要去右范围
    if(m+1<=jobr)
    {
        ans=max(ans,query(jobl,jobr,m+1,r,i<<1|1));
    }
    return ans;
}

void randomArray(int n,int v)
{
    for(int i=1;i<=n;i++)
    {
        arr[i]=rand()%v;
    }
}

void checkUpdate(int jobl,int jobr,ll jobv,vector<ll>&check)
{
    for(int i=jobl;i<=jobr;i++)
    {
        check[i]=jobv;
    }
}

ll checkQuery(int jobl,int jobr,vector<ll>&check)
{
    ll ans=-1e9;
    for(int i=jobl;i<=jobr;i++)
    {
        ans=max(ans,check[i]);
    }
    return ans;
}

void solve()
{
    srand(time(0));

    int N=1000;
    int V=2000;
    int T=5000000;
    
    randomArray(N,V);

    //建立
    build(1,N,1);

    //生成验证结构
    vector<ll>check(N+1);
    for(int i=1;i<=N;i++)
    {
        check[i]=arr[i];
    }

    cout<<"Start"<<endl;
    for(int i=1;i<=T;i++)
    {
        int op=rand()%2;

        //随机加标
        int x=rand()%N+1;
        int y=rand()%N+1;

        int jobl=min(x,y);
        int jobr=max(x,y);

        if(op==0)//更新
        {
            int jobv=rand()%(V*2)-V;
            change(jobl,jobr,jobv,1,N,1);
            checkUpdate(jobl,jobr,jobv,check);
        }
        else//查询
        {
            ll ans1=query(jobl,jobr,1,N,1);
            ll ans2=checkQuery(jobl,jobr,check);

            if(ans1!=ans2)
            {
                cout<<"Wrong"<<endl;
            }
        }
    }
    cout<<"Over"<<endl;
}

int main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--)
    {
        solve();    
    }
    return 0;
}

这个就是缝合了一下前面两个题，没啥好说的。

5.范围重置增加查询且维护累加和

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;

const int MAXN=1e5+5;

vector<ll>arr(MAXN);

//开4倍空间
//累加和数组
vector<ll>sum(MAXN<<2);
//增加数组
vector<ll>ad(MAXN<<2);
//重置数组
vector<ll>chg(MAXN<<2);
//重置任务是否没往下发
vector<bool>update(MAXN<<2);

//更新重置信息
void updateLazy(int i,ll v,int n)
{
    sum[i]=v*n;
    chg[i]=v;

    //清空增加信息
    ad[i]=0;
   
    //更新过了，但还没往下发
    update[i]=true;
}

//更新累加和
void addLazy(int i,ll v,int n)
{
    sum[i]+=v*n;
    ad[i]+=v;
}

//信息汇总
void up(int i)
{
    sum[i]=sum[i<<1]+sum[i<<1|1];
}

//懒信息下发
//ln:左范围个数 rn:右范围个数
void down(int i,int ln,int rn)
{
    //不管前面加了多少，只要来了重置信息，直接清零
    //所以如果既有重置又有增加，那么一定先进行重置

    //先处理重置操作
    if(update[i])
    {
        //往左范围发
        updateLazy(i<<1,chg[i],ln);
 
       //往右范围发
        updateLazy(i<<1|1,chg[i],rn);
 
        //更新结束，修改状态
        update[i]=false;
    }
    //后处理增加信息
    if(ad[i]!=0)
    {
        addLazy(i<<1,ad[i],ln);
        addLazy(i<<1|1,ad[i],rn);
        ad[i]=0;
    }
}

//构建
void build(int l,int r,int i)
{
    if(l==r)//叶节点
    {
        sum[i]=arr[l];
    }
    else
    {
        int m=(l+r)>>1;

        //左范围
        build(l,m,i<<1);
        //右范围
        build(m+1,r,i<<1|1);

        //统计累加和
        up(i);
    }
    //初始没有懒信息，也不需要往下发
    ad[i]=0;
    chg[i]=0;
    update[i]=false;
}

//范围增加
void add(int jobl,int jobr,ll jobv,int l,int r,int i)
{
    if(jobl<=l&&r<=jobr)
    {
        addLazy(i,jobv,r-l+1);
    }
    else
    {
        int m=(l+r)>>1;

        down(i,m-l+1,r-m);

        if(jobl<=m)
        {
            add(jobl,jobr,jobv,l,m,i<<1);
        }
        if(m+1<=jobr)
        {
            add(jobl,jobr,jobv,m+1,r,i<<1|1);
        }

        up(i);
    }
}

//范围重置
void change(int jobl,int jobr,ll jobv,int l,int r,int i)
{
    if(jobl<=l&&r<=jobr)//被全包了
    {
        //直接更新
        updateLazy(i,jobv,r-l+1);
    }
    else
    {
        int m=(l+r)>>1;

        //下发懒信息
        down(i,m-l+1,r-m);

        //需要去左范围
        if(jobl<=m)
        {   
            change(jobl,jobr,jobv,l,m,i<<1);
        }
        //需要去右范围
        if(m+1<=jobr)
        {
            change(jobl,jobr,jobv,m+1,r,i<<1|1);
        }

        //汇总
        up(i);
    }
}

//范围查询
ll query(int jobl,int jobr,int l,int r,int i)
{
    //被全包了
    if(jobl<=l&&r<=jobr)
    {
        return sum[i];
    }

    //没被全包，需要往下扎
    int m=(l+r)>>1;

    //下发懒信息
    down(i,m-l+1,r-m);
    
    ll ans=0;
    //需要去左范围
    if(jobl<=m)
    {
        ans+=query(jobl,jobr,l,m,i<<1);
    }
    //需要去右范围
    if(m+1<=jobr)
    {
        ans+=query(jobl,jobr,m+1,r,i<<1|1);
    }
    return ans;
}

void randomArray(int n,int v)
{
    for(int i=1;i<=n;i++)
    {
        arr[i]=rand()%v;
    }
}

void checkAdd(int jobl,int jobr,ll jobv,vector<ll>&check)
{
    for(int i=jobl;i<=jobr;i++)
    {
        check[i]+=jobv;
    }
}

void checkUpdate(int jobl,int jobr,ll jobv,vector<ll>&check)
{
    for(int i=jobl;i<=jobr;i++)
    {
        check[i]=jobv;
    }
}

ll checkQuery(int jobl,int jobr,vector<ll>&check)
{
    ll ans=0;
    for(int i=jobl;i<=jobr;i++)
    {
        ans+=check[i];
    }
    return ans;
}

void solve()
{
    srand(time(0));

    int N=1000;
    int V=2000;
    int T=5000000;
    
    randomArray(N,V);

    //建立
    build(1,N,1);

    //生成验证结构
    vector<ll>check(N+1);
    for(int i=1;i<=N;i++)
    {
        check[i]=arr[i];
    }

    cout<<"Start"<<endl;
    for(int i=1;i<=T;i++)
    {
        int op=rand()%3;

        //随机加标
        int x=rand()%N+1;
        int y=rand()%N+1;

        int jobl=min(x,y);
        int jobr=max(x,y);

        if(op==0)//更新
        {
            int jobv=rand()%(V*2)-V;
            change(jobl,jobr,jobv,1,N,1);
            checkUpdate(jobl,jobr,jobv,check);
        }
        else if(op==1)//增加
        {
            int jobv=rand()%(V*2)-V;
            add(jobl,jobr,jobv,1,N,1);
            checkAdd(jobl,jobr,jobv,check);
        }
        else//查询
        {
            ll ans1=query(jobl,jobr,1,N,1);
            ll ans2=checkQuery(jobl,jobr,check);

            if(ans1!=ans2)
            {
                cout<<"Wrong"<<endl;
            }
        }
    }
    cout<<"Over"<<endl;
}

int main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--)
    {
        solve();    
    }
    return 0;
}

这个题就需要一点小思考了。

这个题的变化就是需要处理增加信息和重置信息的先后问题。思考一下就可以发现，不管前面进行了多少次增加操作，只要现在来了一个重置操作，那么前面的增加操作都没意义。那么当同时有增加信息和重置信息时，一定是重置信息在前。所以，down函数里就是先处理重置信息，再处理增加信息。在updateLazy里，更新完之后还要把ad数组的增加信息清空。

6.扶苏的问题

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;

const int MAXN=1e6+5;

vector<ll>arr(MAXN);

//开4倍空间
//最大值数组
vector<ll>mx(MAXN<<2);
//增加数组
vector<ll>ad(MAXN<<2);
//重置数组
vector<ll>chg(MAXN<<2);
//重置任务是否没往下发
vector<bool>update(MAXN<<2);

//更新重置信息
void updateLazy(int i,ll v)
{
    mx[i]=v;
    chg[i]=v;

    //清空增加信息
    ad[i]=0;
   
    //更新过了，但还没往下发
    update[i]=true;
}

//更新累加和
void addLazy(int i,ll v)
{
    mx[i]+=v;
    ad[i]+=v;
}

//信息汇总
void up(int i)
{
    mx[i]=max(mx[i<<1],mx[i<<1|1]);
}

//懒信息下发
//ln:左范围个数 rn:右范围个数
void down(int i)
{
    //不管前面加了多少，只要来了重置信息，直接清零
    //所以如果既有重置又有增加，那么一定先进行重置

    //先处理重置操作
    if(update[i])
    {
        //往左范围发
        updateLazy(i<<1,chg[i]);
 
       //往右范围发
        updateLazy(i<<1|1,chg[i]);
 
        //更新结束，修改状态
        update[i]=false;
    }
    //后处理增加信息
    if(ad[i]!=0)
    {
        addLazy(i<<1,ad[i]);
        addLazy(i<<1|1,ad[i]);
        ad[i]=0;
    }
}

//构建
void build(int l,int r,int i)
{
    if(l==r)//叶节点
    {
        mx[i]=arr[l];
    }
    else
    {
        int m=(l+r)>>1;

        //左范围
        build(l,m,i<<1);
        //右范围
        build(m+1,r,i<<1|1);

        //统计累加和
        up(i);
    }
    //初始没有懒信息，也不需要往下发
    ad[i]=0;
    chg[i]=0;
    update[i]=false;
}

//范围增加
void add(int jobl,int jobr,ll jobv,int l,int r,int i)
{
    if(jobl<=l&&r<=jobr)
    {
        addLazy(i,jobv);
    }
    else
    {
        int m=(l+r)>>1;

        down(i);

        if(jobl<=m)
        {
            add(jobl,jobr,jobv,l,m,i<<1);
        }
        if(m+1<=jobr)
        {
            add(jobl,jobr,jobv,m+1,r,i<<1|1);
        }

        up(i);
    }
}

//范围重置
void change(int jobl,int jobr,ll jobv,int l,int r,int i)
{
    if(jobl<=l&&r<=jobr)//被全包了
    {
        //直接更新
        updateLazy(i,jobv);
    }
    else
    {
        int m=(l+r)>>1;

        //下发懒信息
        down(i);

        //需要去左范围
        if(jobl<=m)
        {   
            change(jobl,jobr,jobv,l,m,i<<1);
        }
        //需要去右范围
        if(m+1<=jobr)
        {
            change(jobl,jobr,jobv,m+1,r,i<<1|1);
        }

        //汇总
        up(i);
    }
}

//范围查询
ll query(int jobl,int jobr,int l,int r,int i)
{
    //被全包了
    if(jobl<=l&&r<=jobr)
    {
        return mx[i];
    }

    //没被全包，需要往下扎
    int m=(l+r)>>1;

    //下发懒信息
    down(i);
    
    ll ans=-1e18;
    //需要去左范围
    if(jobl<=m)
    {
        ans=max(ans,query(jobl,jobr,l,m,i<<1));
    }
    //需要去右范围
    if(m+1<=jobr)
    {
        ans=max(ans,query(jobl,jobr,m+1,r,i<<1|1));
    }
    return ans;
}

void solve()
{
    int n,q;
    cin>>n>>q;
    for(int i=1;i<=n;i++)
    {
        cin>>arr[i];
    }

    build(1,n,1);

    int op;
    while(q--)
    {
        cin>>op;

        if(op==1)//修改
        {
            int l,r;
            ll x;
            cin>>l>>r>>x;

            change(l,r,x,1,n,1);
        }
        else if(op==2)//增加
        {
            int l,r;
            ll x;
            cin>>l>>r>>x;

            add(l,r,x,1,n,1);
        }
        else
        {
            int l,r;
            cin>>l>>r;

            cout<<query(l,r,1,n,1)<<endl;
        }
    }
}

int main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--)
    {
        solve();    
    }
    return 0;
}

这个题在上个题的基础上改成维护最大值即可。

总结

提高效率，加油！！

END

热门推荐
01UV安装并设置国内源02Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code03DeepSeek更新！速览DeepSeek V3.1新特性04KGG转MP3工具|非KGM文件|解密音频05蜘蛛磁力 搜索引擎大全，如何使用蜘蛛磁力查找磁力链接06【2025.08.06最新版】Android Studio下载、安装及配置记录（自动下载sdk）072025最新国内服务器可用docker源仓库地址大全（2025年8月更新）08NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南09阿里开源首个图像生成基础模型——Qwen-Image本地部署教程，超强中文渲染能力刷新SOTA！10TRAE 规则（Rules）配置指南：个人习惯、团队规范与最佳实践