算法第四十九天：单调栈part02（第十章）

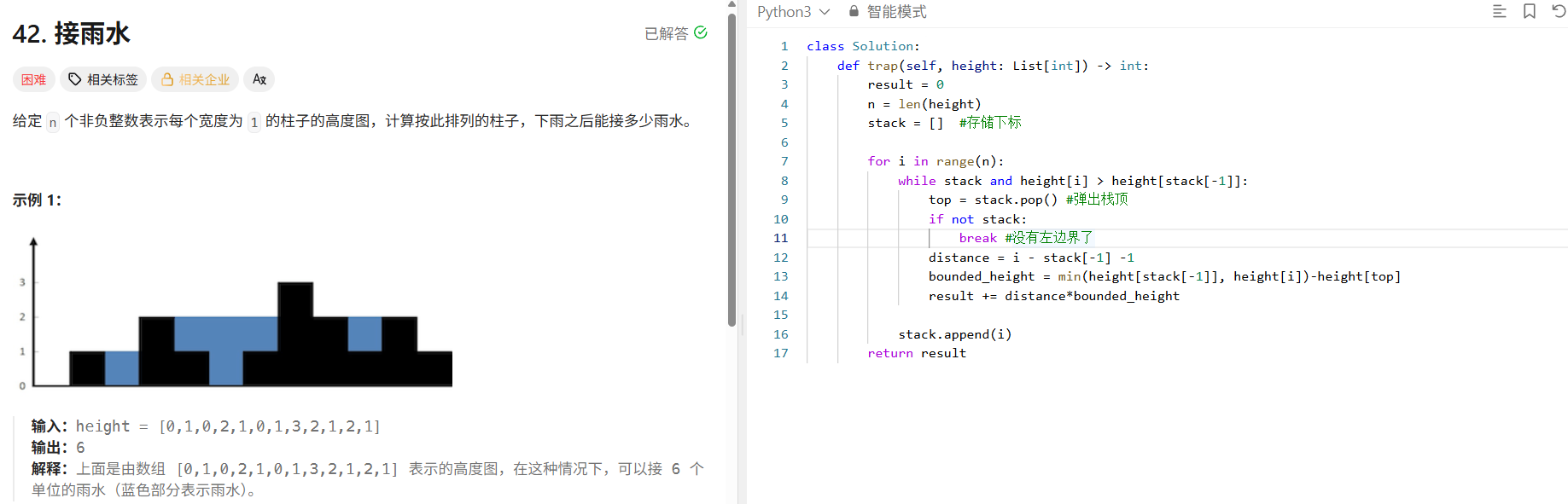
1.接雨水

1️⃣ 算法核心思想

用一个单调栈存储柱子下标，保持栈内从栈底到栈顶柱子高度递减。
遍历每根柱子：
1. 如果当前柱子高度比栈顶柱子高，说明可能形成"坑"，可以计算雨水。
2. 弹出栈顶柱子 top，计算以 top 为底的雨水面积：
  - 宽度 = 当前柱子下标 i - 左边界下标 stack[-1] - 1
  - 高度 = min(height[i], height[stack[-1]]) - height[top]
  - 面积 = 宽度 × 高度
3. 将当前柱子下标入栈作为新的右边界或潜在左边界。

2️⃣ 宽度不是 1 的原因

一个坑可能跨越多个柱子，中间低柱子形成积水。

宽度 = 左右边界下标差 - 1，确保只计算中间的空位。

class Solution:
def trap(self, height: List[int]) -> int:
result = 0
n = len(height)
stack = [] #存储下标

复制代码

      for i in range(n):
          while stack and height[i] > height[stack[-1]]:
              top = stack.pop() #弹出栈顶
              if not stack:
                  break #没有左边界了
              distance = i - stack[-1] -1 
              bounded_height = min(height[stack[-1]], height[i])-height[top]
              result += distance*bounded_height
              
          stack.append(i)
      return result

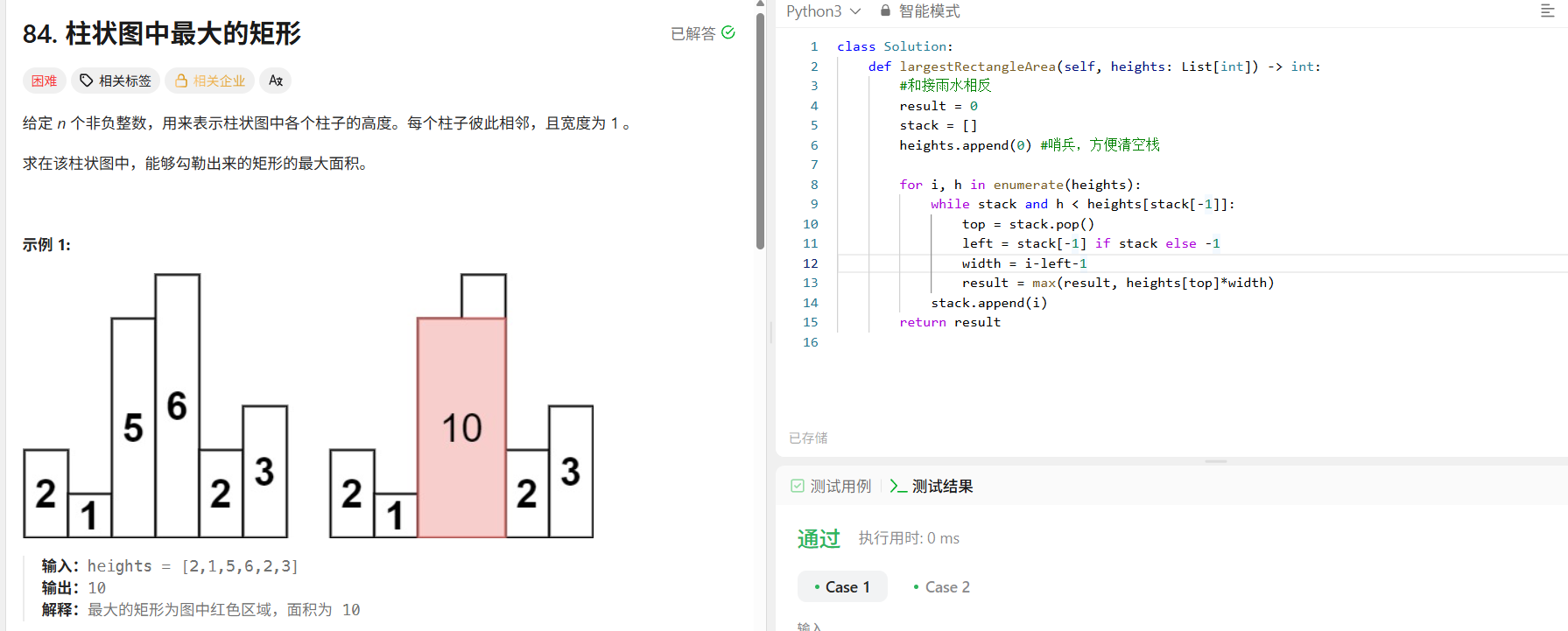
2.柱状图中最大的矩形

思路：

1️⃣ 栈的作用

栈中存储 柱子的下标，便于计算矩形宽度。
栈保持 高度递增。
当当前柱子比栈顶低时，说明栈顶柱子的右边界到此为止，可以计算矩形面积。

2️⃣ 面积计算公式

当弹出栈顶 top 时：

高度：height[top]
宽度：width = i - left - 1
- i = 当前下标（右边界）
- left = 弹出后栈顶下标（左边界）
- 如果栈空 → 左边界不存在 → left = -1
面积：area = height[top] * width
更新最大面积：max_area = max(max_area, area)

3️⃣ 栈的操作流程

遍历每根柱子：
- 栈空或当前柱子 ≥ 栈顶柱子 → 入栈
- 当前柱子 < 栈顶柱子 → 弹栈计算面积，重复直到栈空或栈顶柱子 ≤ 当前柱子
遍历结束后，栈中可能还有未处理柱子，可以在末尾加一个 哨兵 0，清空栈，保证所有柱子都计算面积。

4️⃣ 宽度直观理解

宽度 = 右边界 - 左边界 - 1
因为矩形可以向左扩展到 栈顶左边界的右边一格，不包含左边界本身
右边界是当前柱子下标（比弹出柱子低），不包含在矩形中

如果中间有多个低柱子，宽度可以 >1

class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
#和接雨水相反
result = 0
stack = []
heights.append(0) #哨兵，方便清空栈

复制代码

      for i, h in enumerate(heights):
          while stack and h < heights[stack[-1]]:
              top = stack.pop()
              left = stack[-1] if stack else -1
              width = i-left-1
              result = max(result, heights[top]*width)
          stack.append(i)
      return result

今日份结束！