目录

前言
在图论与网格问题中,最常见的一类题目就是"求最短距离"。通常情况下,我们会从某一个起点出发,利用 BFS(广度优先搜索) 逐层扩展,得到从该点到所有点的最短路。然而,在许多实际场景中,往往存在 多个起点:例如从多个水源扩展到所有陆地、从多个火源蔓延到整个森林,或者像 LeetCode 1162. 地图分析中,从所有陆地出发,计算到最远海洋的距离。
这类问题的核心思想就是 BFS 多源最短路。它与单源 BFS 不同的地方在于:
将所有起点一开始就同时加入队列,作为 BFS 的第一层;
在层层扩展的过程中,天然保证了最短路的正确性;
代码实现上非常简洁,不需要额外的多次 BFS。
前提引入
-
图 可以有方向/无方向;边可以有权重(花费/距离/时间)。
-
最短路:从 A 到 B 的最小代价之和。
常见几种场景:
-
单源最短路(SSSP):从一个起点 s 到所有点的最短路。
-
多源最短路(两种含义):
-
多起点→所有点:有好几个起点,一起"向外扩散";
-
任意两点 (全源/全对,APSP):所有点到所有点的最短路。
-
多源最短路两种玩法
多起点 → 所有点(常见于"多个出发点最近距离")
-
无权图 :把所有起点一起入队 ,做一次 BFS (上面的
bfs_multi_source就是)。 -
有权非负 :把所有起点 dist=0,一起入堆 ,做一次 Dijkstra。
-
有负边 :加一个超级源点 S,连向每个起点一条权重为 0 的边,然后 Bellman--Ford 或其他方案。
谈谈多源最短路
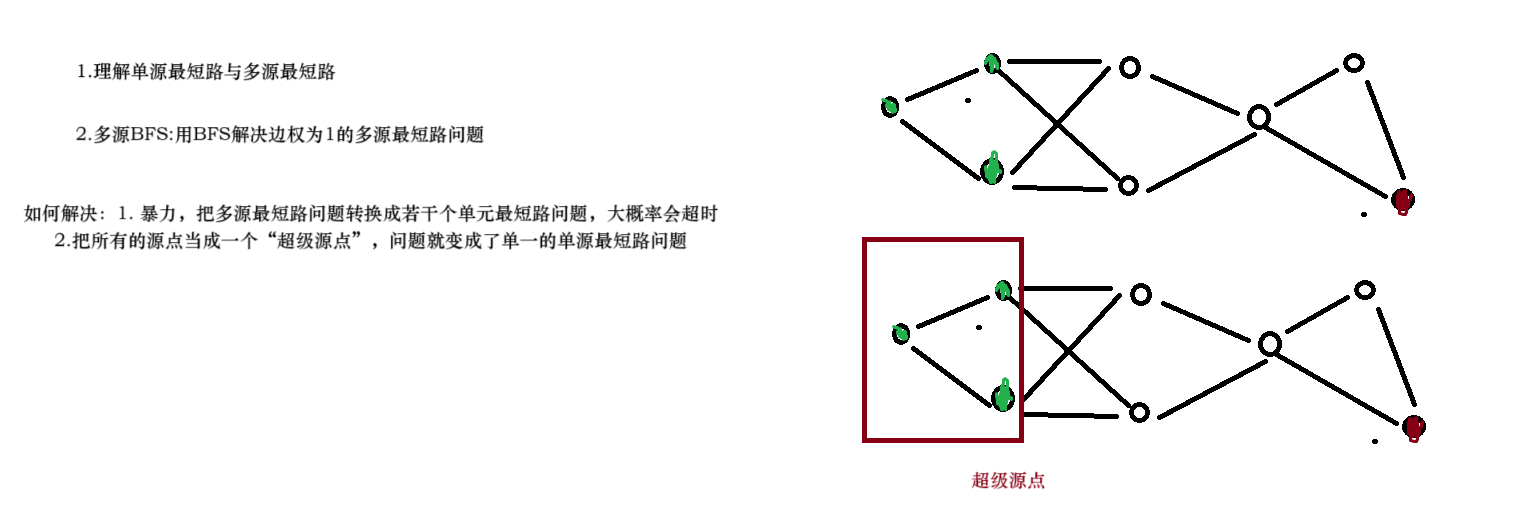
如何解决:1. 暴力,把多源最短路问题转换成若干个单元最短路问题,大概率会超时
2.把所有的源点当成一个"超级源点",问题就变成了单一的单源最短路问题
从理性角度需要严谨的证明,从感性理解上,就是多个起点出发,向外扩展时,舍劣取优
在代码层面,把所有的起点加入到队列里面,一层一层的向外扩展。
题目实练
矩阵
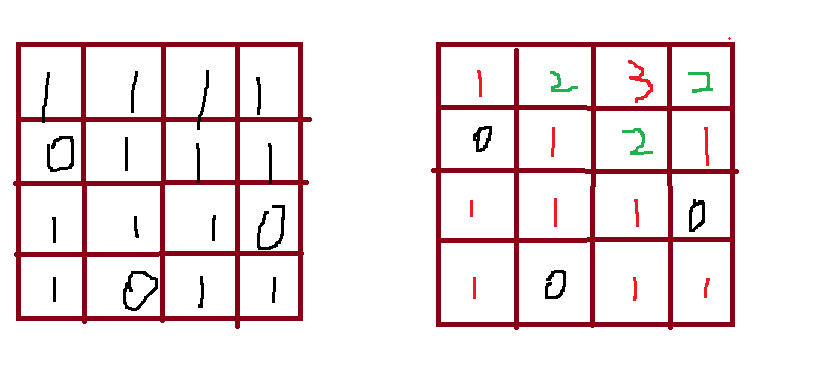
给定一个由
0和1组成的矩阵mat,请输出一个大小相同的矩阵,其中每一个格子是mat中对应位置元素到最近的0的距离。两个相邻元素间的距离为
1。
一个一个位置求,每个位置来一趟BFS,这样子会超时的。
多源BFS+正难则反,把所有的0当做起点,1当做终点,这样1的位置就直接填结果,按照原先1找0还有倒退写值。
把所有的0加入到队列中,一层一层的向外扩展即可。
cpp
class Solution {
int dx[4]={0,0,-1,1};
int dy[4]={1,-1,0,0};
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
int n=mat.size(),m=mat[0].size();
vector<vector<int>> dict(n,vector<int>(m,-1));
//dict[i][j]==-1,没有访问 ,!=-1,最短距离,
queue<pair<int,int>>q;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(mat[i][j]==0){
q.push({i,j});
dict[i][j]=0;
}
}
}
while(q.size()){
auto[a,b]=q.front();
q.pop();
for(int i=0;i<4;i++){
int x=a+dx[i];
int y=b+dy[i];
if(x>=0 && x<n && y>=0 && y<m && dict[x][y]==-1){
dict[x][y]=dict[a][b]+1;
q.push({x,y});
}
}
}
return dict;
}
};飞地的数量
给你一个大小为
m x n的二进制矩阵grid,其中0表示一个海洋单元格、1表示一个陆地单元格。一次 移动 是指从一个陆地单元格走到另一个相邻(上、下、左、右 )的陆地单元格或跨过
grid的边界。返回网格中无法在任意次数的移动中离开网格边界的陆地单元格的数量。

-
核心思想:反向思考
与其找"飞地",不如先把 能连到边界的陆地 标记掉。
剩下的没标记的陆地,就是飞地。 -
实现步骤
-
从边界出发,把所有相连的陆地用 BFS/DFS 标记
-
遍历整个网格,统计没被标记的陆地数量
-
cpp
class Solution {
int dx[4]={0,0,-1,1};
int dy[4]={1,-1,0,0};
public:
int numEnclaves(vector<vector<int>>& grid) {
int m=grid.size(),n=grid[0].size();
vector<vector<bool>>vis(m,vector<bool>(n));
queue<pair<int,int>>q;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(i==0 || i==m-1 || j==0 || j==n-1){
if(grid[i][j]==1){
q.push({i,j});
vis[i][j]=true;
}
}
}
}
while(q.size()){
auto [a,b]=q.front();
//grid[a][b]=0;
q.pop();
for(int i=0;i<4;i++){
int x=a+dx[i];
int y=b+dy[i];
if(x>=0 && x<m && y>=0 && y<n && grid[x][y]==1 && !vis[x][y]){
q.push({x,y});
// grid[x][y]=0;
vis[x][y]=true;
}
}
}
int num=0;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j] && !vis[i][j])
num++;
}
}
return num;
}
};-
BFS 遍历时,从边界所有
1出发,把能到达的全部标记 -
最终只数 没被标记的陆地,就是飞地
地图中的最高点
给你一个大小为
m x n的整数矩阵isWater,它代表了一个由 陆地 和 水域 单元格组成的地图。
- 如果
isWater[i][j] == 0,格子(i, j)是一个 陆地 格子。- 如果
isWater[i][j] == 1,格子(i, j)是一个 水域 格子。你需要按照如下规则给每个单元格安排高度:
- 每个格子的高度都必须是非负的。
- 如果一个格子是 水域 ,那么它的高度必须为
0。- 任意相邻的格子高度差 至多 为
1。当两个格子在正东、南、西、北方向上相互紧挨着,就称它们为相邻的格子。(也就是说它们有一条公共边)找到一种安排高度的方案,使得矩阵中的最高高度值 最大 。
请你返回一个大小为
m x n的整数矩阵height,其中height[i][j]是格子(i, j)的高度。如果有多种解法,请返回 任意一个 。

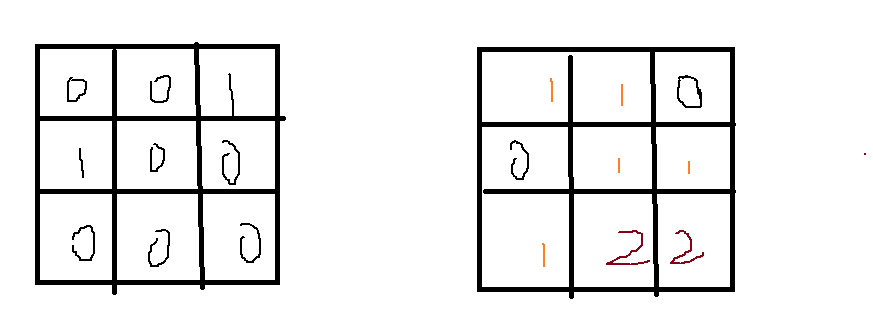
本题就是第一个练习题的变式
cpp
class Solution {
int dx[4]={0,0,-1,1};
int dy[4]={1,-1,0,0};
public:
vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {
int n=isWater.size(),m=isWater[0].size();
vector<vector<int>> vis(n,vector<int>(m,-1));
queue<pair<int,int>> q;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++){
if(isWater[i][j]==1){
vis[i][j]=0;
q.push({i,j});
}
}
while(q.size()){
auto[a,b]=q.front();
q.pop();
for(int i=0;i<4;i++){
int x=a+dx[i];
int y=b+dy[i];
if(x>=0 && x<n && y>=0 && y<m && vis[x][y]==-1){
vis[x][y]=vis[a][b]+1;
q.push({x,y});
}
}
}
return vis;
}
};地图分析
你现在手里有一份大小为
n x n的 网格grid,上面的每个 单元格 都用0和1标记好了。其中0代表海洋,1代表陆地。请你找出一个海洋单元格,这个海洋单元格到离它最近的陆地单元格的距离是最大的,并返回该距离。如果网格上只有陆地或者海洋,请返回
-1。我们这里说的距离是「曼哈顿距离」( Manhattan Distance):
(x0, y0)和(x1, y1)这两个单元格之间的距离是|x0 - x1| + |y0 - y1|。

题目要找:每个海洋格子到最近陆地的距离 的最大值。
这就是一个典型的最短路到最近源点 的问题:如果把所有陆地当作"源点",那么每个海洋格子的最短距离就是从这些源点出发的 BFS 层数。
核心思路(多源 BFS)
-
把所有陆地(1)同时入队
-
建一个
queue<pair<int,int>> q。 -
建一个距离/访问数组
vis,初值都为-1(表示未访问/未知距离)。 -
遍历网格,若
grid[i][j]==1,则vis[i][j]=0,并q.push({i,j})。这样就等价于从所有陆地同时作为起点,向四周一圈一圈地扩散。
-
-
从陆地向外层层扩散(BFS)
-
出队一个格子
(a,b),尝试 4 个方向(x,y)。 -
若
(x,y)没越界、且vis[x][y]==-1(还没确定过距离),就设
vis[x][y]=vis[a][b]+1,把(x,y)入队。 -
这一步保证了 第一次到达某海洋格子时 走的是最短路径(BFS性质)。
-
-
记录答案
-
在给某个新格子赋值
vis[x][y]=vis[a][b]+1的同时,用ret=max(ret, vis[x][y])维护目前最大的距离。 -
BFS 完毕后返回
ret。
-
为什么不用额外写两种边界判断
-
全是海洋 :初始队列为空,
while(q.size())不执行,ret保持-1,直接返回-1✅ -
全是陆地 :所有陆地进队,但周围没有"未访问的海洋"可扩展,
ret从头到尾未更新,仍为-1,返回-1✅ -
既有陆地也有海洋 :扩散会把海洋逐层更新,
ret会被更新到最大层数(最远的海洋到最近陆地的距离)✅
FS 从所有陆地同时出发,按"层"向外扩展。第一次访问到的海洋格子,其层数就是它到最近陆地的最短步数;后来再访问到它的路径只会更长,不会更短。于是每个海洋的 vis 值都恰好是到最近陆地的距离。最大值自然是题目要的答案。
结束语
BFS 多源最短路 的关键,在于利用队列并行扩展所有起点,避免了重复计算,也保证了结果的全局最优。它是 BFS 思想在实际问题中的一种高效变形,常见于网格扩散、距离计算、最短传播路径等题型中。
掌握这种方法后,你会发现:只要问题中存在"从一批点出发、寻找离它们最远或最近的点"的场景,往往都能一眼识别出是 多源 BFS 的典型应用。