有向无环图（Directed Acyclic Graph, DAG）介绍（环检测、DFS法、Kahn算法、）

https://www.bilibili.com/video/BV1mY4y1V7kH

文章目录

• 有向无环图（DAG）介绍
• • [1. **边的方向性**：每条边都有明确的方向（如从顶点 A → B A \rightarrow B A→B，与 B → A B \rightarrow A B→A 不同）。](#1. 边的方向性：每条边都有明确的方向（如从顶点 A → B A \rightarrow B A→B，与 B → A B \rightarrow A B→A 不同）。)
  • [2. **无环性**：图中不存在任何形式的环路，即无法从某个顶点出发，沿着边最终回到起点。](#2. 无环性：图中不存在任何形式的环路，即无法从某个顶点出发，沿着边最终回到起点。)
  • **关键特性**
  • • [1. **拓扑排序可行性**](#1. 拓扑排序可行性)
    • [2. **入度与出度**](#2. 入度与出度)
    • [3. **子结构共享**](#3. 子结构共享)
  • **应用场景**
  • • [1. **任务调度与依赖管理**](#1. 任务调度与依赖管理)
    • • [- **课程安排**：根据课程的先修要求，确定选课顺序（如线性代数需在微积分之前学习）。](#- 课程安排：根据课程的先修要求，确定选课顺序（如线性代数需在微积分之前学习）。)
      • [- **编译器优化**：通过 DAG 共享公共子表达式，减少重复计算（如表达式 `((a+b)*(c+d))` 的优化）。](#- 编译器优化：通过 DAG 共享公共子表达式，减少重复计算（如表达式 ((a+b)*(c+d)) 的优化）。)
      • [- **项目管理**：安排任务的执行顺序（如软件开发中的模块依赖）。](#- 项目管理：安排任务的执行顺序（如软件开发中的模块依赖）。)
    • [2. **数据流处理**](#2. 数据流处理)
    • • [- **Apache Airflow**：工作流调度工具，通过 DAG 表示任务之间的依赖关系。](#- Apache Airflow：工作流调度工具，通过 DAG 表示任务之间的依赖关系。)
      • [- **区块链技术**：IOTA 的 Tangle 技术利用 DAG 结构提升交易处理效率（与传统区块链的链式结构不同）。](#- 区块链技术：IOTA 的 Tangle 技术利用 DAG 结构提升交易处理效率（与传统区块链的链式结构不同）。)
    • [3. **版本控制系统**](#3. 版本控制系统)
    • • [- **Git**：提交历史的合并结构（如分支和合并操作）形成 DAG，而非线性链表。](#- Git：提交历史的合并结构（如分支和合并操作）形成 DAG，而非线性链表。)
    • [4. **最短/最长路径问题**](#4. 最短/最长路径问题)
    • • [- DAG 上的最短路径和最长路径（关键路径）可以通过拓扑排序在 O ( V + E ) O(V + E) O(V+E) 时间内高效求解。](#- DAG 上的最短路径和最长路径（关键路径）可以通过拓扑排序在 O ( V + E ) O(V + E) O(V+E) 时间内高效求解。)
  • [**DAG 的算法与操作**](#DAG 的算法与操作)
  • • [1. **环检测**](#1. 环检测)
    • • [- **DFS 法**：深度优先搜索时维护递归栈，若遇到已访问且仍在栈中的节点，则存在环。](#- DFS 法：深度优先搜索时维护递归栈，若遇到已访问且仍在栈中的节点，则存在环。)
      • [- **Kahn 算法**：通过入度统计和队列处理判断是否存在环（拓扑排序的变种）。](#- Kahn 算法：通过入度统计和队列处理判断是否存在环（拓扑排序的变种）。)
    • [2. **拓扑排序**](#2. 拓扑排序)
    • • [- **Kahn 算法**：](#- Kahn 算法：)
      • [- **DFS 后序逆序**：对 DAG 进行 DFS，按完成时间逆序排列得到拓扑序列。](#- DFS 后序逆序：对 DAG 进行 DFS，按完成时间逆序排列得到拓扑序列。)
    • [3. **最长/最短路径计算**](#3. 最长/最短路径计算)
    • • [- **动态规划法**：按拓扑顺序处理顶点，更新邻接顶点的路径值（适用于带权 DAG）。](#- 动态规划法：按拓扑顺序处理顶点，更新邻接顶点的路径值（适用于带权 DAG）。)
  • [**DAG 与树的区别**](#DAG 与树的区别)
  • [**代码示例：Kahn 算法（JavaScript 实现）**](#代码示例：Kahn 算法（JavaScript 实现）)
  • **总结**

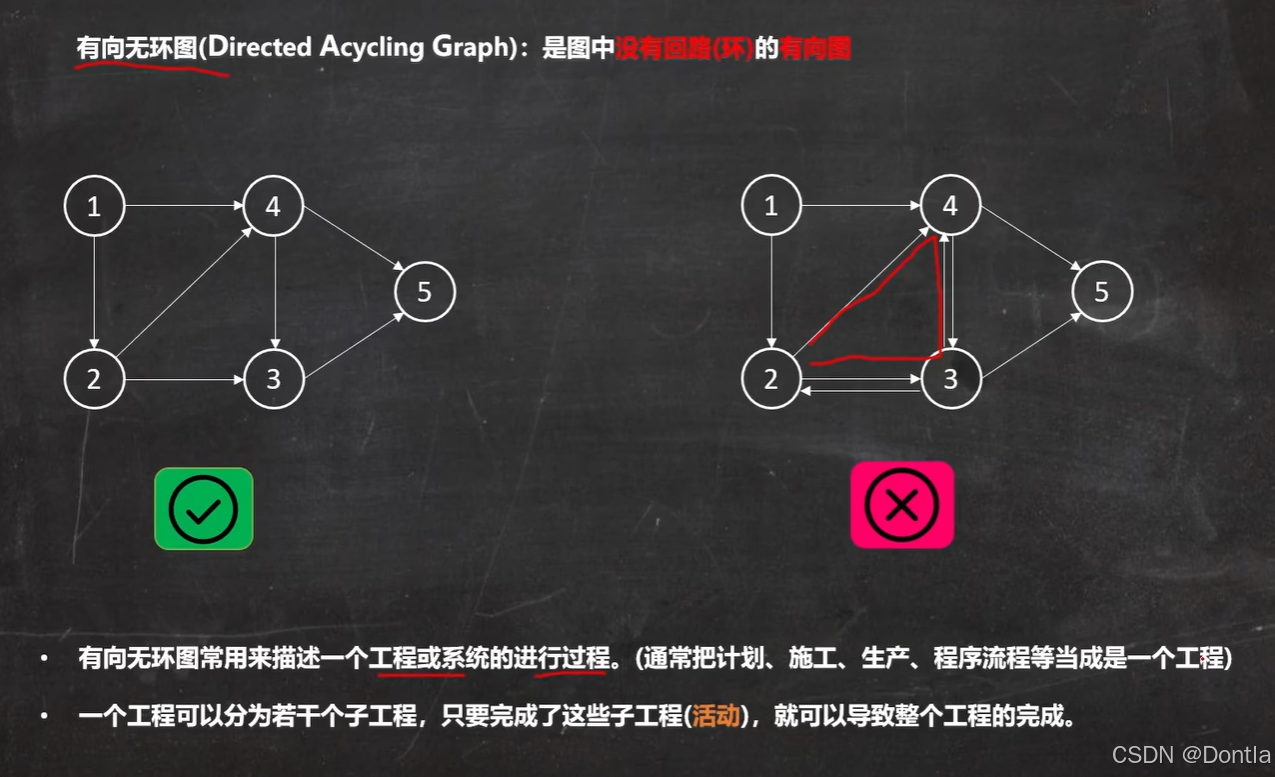
有向无环图（DAG）介绍

有向无环图（Directed Acyclic Graph, DAG） 是一种特殊的有向图，其核心特点是：

1. 边的方向性 ：每条边都有明确的方向（如从顶点 A → B A \rightarrow B A→B，与 B → A B \rightarrow A B→A 不同）。

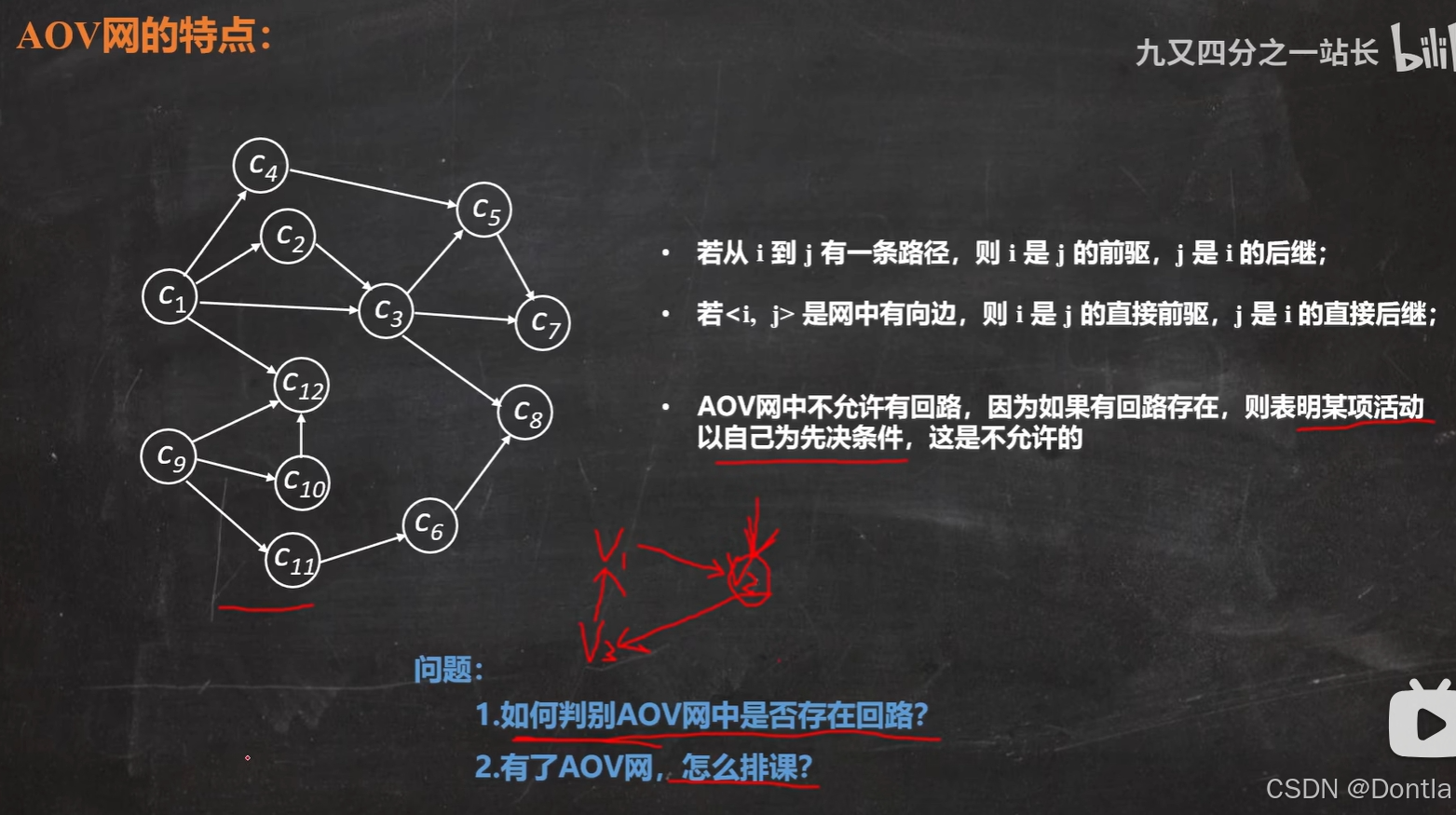
2. 无环性：图中不存在任何形式的环路，即无法从某个顶点出发，沿着边最终回到起点。

---

关键特性

1. 拓扑排序可行性

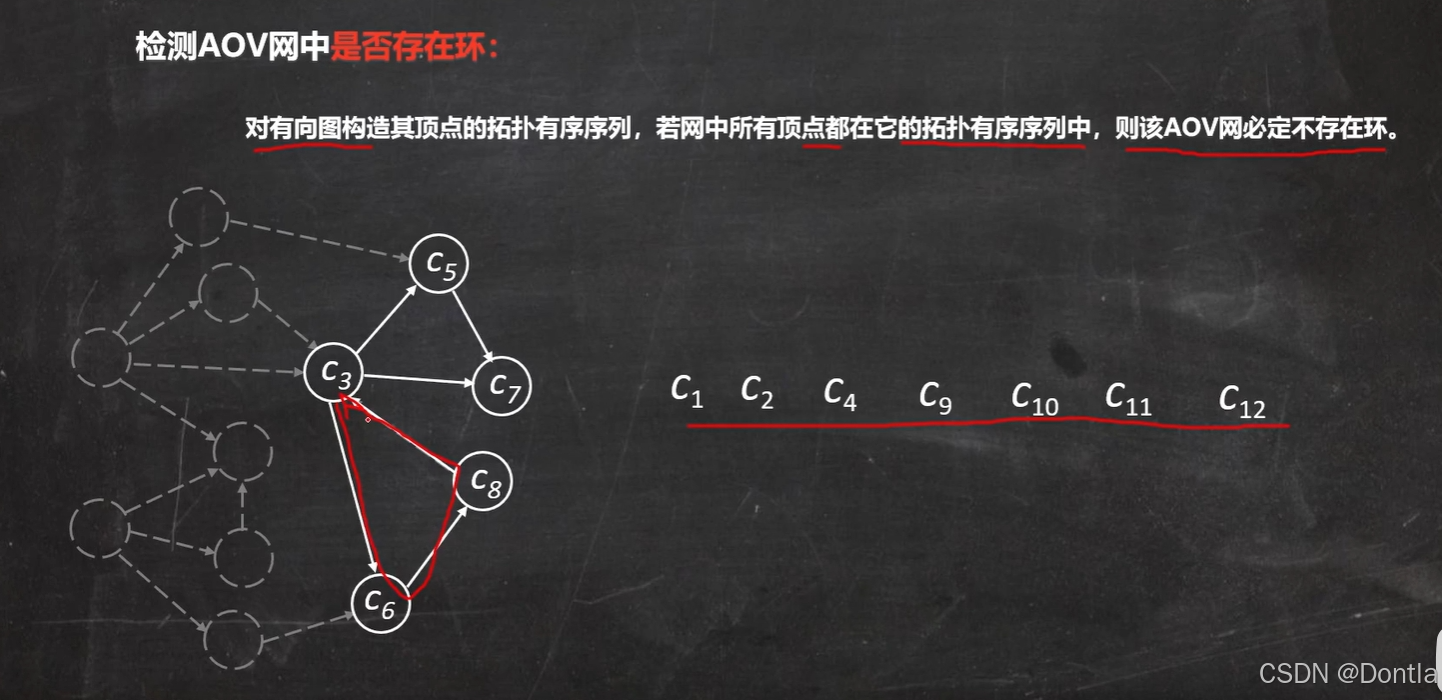
• DAG 必然存在至少一个拓扑排序，即所有顶点可以排成一个线性序列，使得每条边的起点在终点之前。
• 拓扑排序是 DAG 的核心性质，常用于任务调度、依赖管理等问题。

2. 入度与出度

• 每个 DAG 中必然存在至少一个入度为 0 的顶点（无前置依赖），以及至少一个出度为 0 的顶点（无后续依赖）。

3. 子结构共享

• DAG 可以高效表示具有公共子结构的表达式（如编译原理中的基本块优化）。

---

应用场景

1. 任务调度与依赖管理

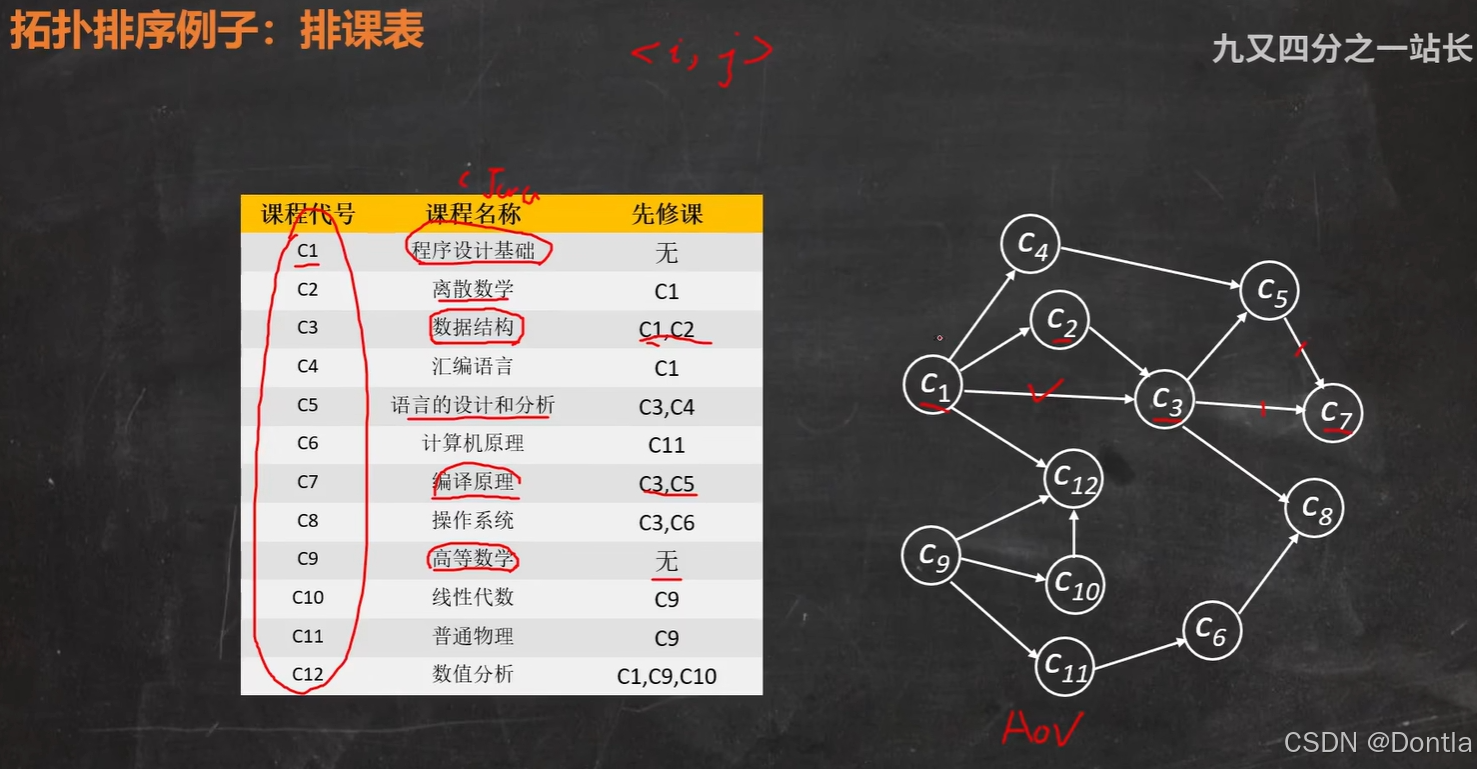
- 课程安排：根据课程的先修要求，确定选课顺序（如线性代数需在微积分之前学习）。

- 编译器优化 ：通过 DAG 共享公共子表达式，减少重复计算（如表达式 ((a+b)*(c+d)) 的优化）。

- 项目管理：安排任务的执行顺序（如软件开发中的模块依赖）。

2. 数据流处理

- Apache Airflow：工作流调度工具，通过 DAG 表示任务之间的依赖关系。

- 区块链技术：IOTA 的 Tangle 技术利用 DAG 结构提升交易处理效率（与传统区块链的链式结构不同）。

3. 版本控制系统

- Git：提交历史的合并结构（如分支和合并操作）形成 DAG，而非线性链表。

4. 最短/最长路径问题

- DAG 上的最短路径和最长路径（关键路径）可以通过拓扑排序在 O ( V + E ) O(V + E) O(V+E) 时间内高效求解。

---

DAG 的算法与操作

1. 环检测

- DFS 法：深度优先搜索时维护递归栈，若遇到已访问且仍在栈中的节点，则存在环。

- Kahn 算法：通过入度统计和队列处理判断是否存在环（拓扑排序的变种）。

2. 拓扑排序

- Kahn 算法：

1. 统计每个顶点的入度。
2. 将入度为 0 的顶点加入队列。
3. 依次处理队列中的顶点，减少其邻居的入度，若邻居入度为 0 则入队。
4. 若最终处理顶点数不等于总顶点数，则图中存在环。

- DFS 后序逆序：对 DAG 进行 DFS，按完成时间逆序排列得到拓扑序列。

3. 最长/最短路径计算

- 动态规划法：按拓扑顺序处理顶点，更新邻接顶点的路径值（适用于带权 DAG）。

---

DAG 与树的区别

特性	树（Tree）	DAG（有向无环图）
方向性	无向或有向（如二叉树）	有向
环路	无环	无环
父节点数	每个节点至多一个父节点	节点可有多个父节点
连通性	连通	可连通或非连通

---

代码示例：Kahn 算法（JavaScript 实现）

function kahnTopologicalSort(graph) {
  const inDegree = {}; // 记录每个节点的入度
  const queue = [];    // 存储入度为 0 的节点
  const result = [];   // 存储拓扑排序结果

  // 初始化入度表
  for (const node in graph) {
    inDegree[node] = 0;
  }

  // 计算每个节点的入度
  for (const node in graph) {
    for (const neighbor of graph[node]) {
      inDegree[neighbor]++;
    }
  }

  // 将入度为 0 的节点加入队列
  for (const node in inDegree) {
    if (inDegree[node] === 0) {
      queue.push(node);
    }
  }

  // 处理队列中的节点
  while (queue.length > 0) {
    const node = queue.shift(); // 取出队首节点
    result.push(node);          // 加入拓扑排序结果

    // 减少相邻节点的入度
    for (const neighbor of graph[node]) {
      inDegree[neighbor]--;
      // 如果相邻节点的入度为 0，加入队列
      if (inDegree[neighbor] === 0) {
        queue.push(neighbor);
      }
    }
  }

  // 检查是否存在环
  if (result.length !== Object.keys(graph).length) {
    throw new Error("图中存在环，无法进行拓扑排序");
  }

  return result;
}

// 示例
const graph = {
  A: ['C'],
  B: ['C', 'D'],
  C: ['E'],
  D: ['F'],
  E: ['H', 'F'],
  F: ['G'],
  G: [],
  H: [],
};

console.log(kahnTopologicalSort(graph)); // 输出: ['A', 'B', 'D', 'C', 'E', 'F', 'H', 'G']

---

总结

DAG 是一种强大的数据结构，广泛应用于任务调度、数据流处理、版本控制等领域。其核心优势在于通过拓扑排序解决依赖问题，并通过动态规划高效计算最短/最长路径。理解 DAG 的特性和算法（如拓扑排序、Kahn 算法）对于解决实际工程问题至关重要。