文章目录
一、概论
机器学习:实现数据驱动的自动化决策。深度学习:机器学习的子集。通过深层网络拟合复杂的非线性关系,处理高维度、复杂结构的数据(如图像、文本)。表示学习:机器学习的一个分支。核心是 特征转换,是连接原始数据与预测模型的桥梁。- 机器学习和深度学习的主要区别是:机器学习为人工处理设计特征,深度学习不需要人工处理。

二、 线性回归
2.1基本概念
输入:结构化的特征数据,通常用向量或矩阵表示。
单个样本的输入为一个
特征向量(1行n列): x = [ x 1 , x 2 , . . . , x n ] x = [x_1, x_2, ..., x_n] x=[x1,x2,...,xn] 其中 n n n 是特征数量(如预测房价时, x 1 x_1 x1 可能是"面积", x 2 x_2 x2 是"房间数")。多个样本的输入为
特征矩阵(m行n列): X = [ x 1 ( 1 ) x 2 ( 1 ) . . . x n ( 1 ) x 1 ( 2 ) x 2 ( 2 ) . . . x n ( 2 ) . . . . . . . . . . . . x 1 ( m ) x 2 ( m ) . . . x n ( m ) ] X = \begin{bmatrix} x_1^{(1)} & x_2^{(1)} & ... & x_n^{(1)} \\ x_1^{(2)} & x_2^{(2)} & ... & x_n^{(2)} \\ ... & ... & ... & ... \\ x_1^{(m)} & x_2^{(m)} & ... & x_n^{(m)} \end{bmatrix} X= x1(1)x1(2)...x1(m)x2(1)x2(2)...x2(m)............xn(1)xn(2)...xn(m) 其中 m m m 是样本数量,每行代表一个样本。输入特征可以是
连续型(如温度、收入)或离散型(需转换为数值形式,如性别,用0/1表示)。特征需经过预处理(如归一化、标准化),避免因数值范围差异影响模型参数学习。
输出:线性回归的输出的连续型数值,代表模型对样本的预测结果。单个样本的输出为一个标量: y ^ \hat{y} y^(如预测的房价500万元)。
多个样本的输出为向量: Y ^ = [ y ^ 1 , y ^ 2 , . . . , y ^ m ] \hat{Y} = [\hat{y}_1, \hat{y}_2, ..., \hat{y}_m] Y^=[y^1,y^2,...,y^m],其中 y ^ i \hat{y}_i y^i 是第 i i i 个样本的预测值。
输出是输入特征的线性组合,公式为: y ^ = w 1 x 1 + w 2 x 2 + . . . + w n x n + b \hat{y} = w_1x_1 + w_2x_2 + ... + w_nx_n + b y^=w1x1+w2x2+...+wnxn+bw 1 , w 2 , . . . , w n w_1, w_2, ..., w_n w1,w2,...,wn 是特征的
权重(表示每个特征对输出的影响程度);b b b 是
偏置项(类似线性方程中的常数项,当所有特征为0时的基准输出)。
y ^ = w T x + b \hat{y} = w^Tx + b y^=wTx+b ( w w w 是权重向量, w T w^T wT 是 w w w 的转置)
2.2模型训练
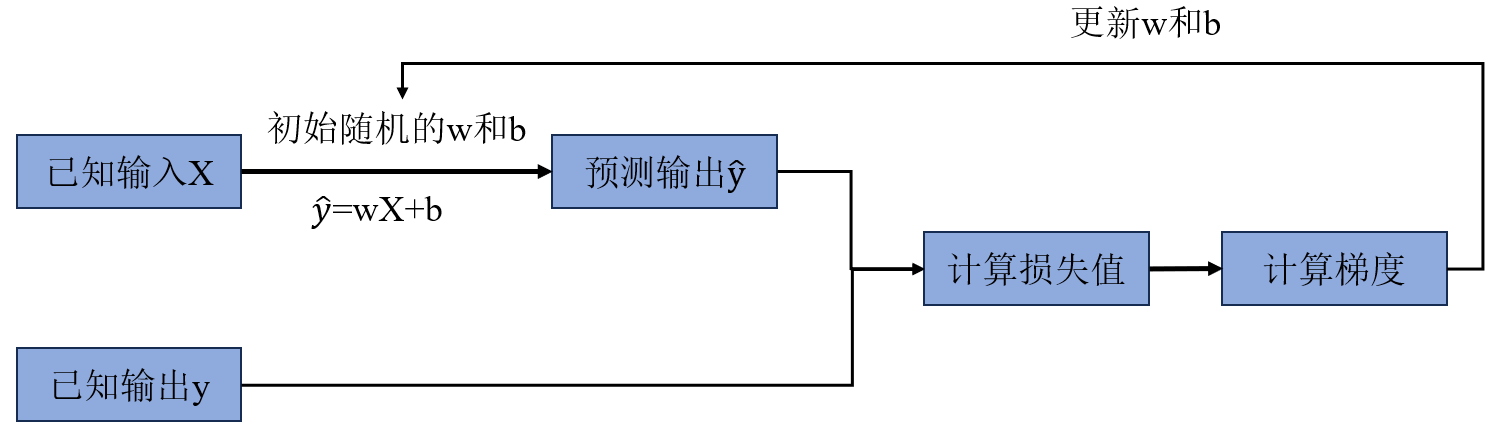
线性回归的核心是通过训练数据学习最优的权重w 和偏置 b,使模型的预测值 y ^ \hat{y} y^ 尽可能接近真实值 y y y。
2.2.1正向传播
正向传播是从 "输入特征" 到 "输出预测值" 再到 "损失计算" 的过程,核心是利用当前参数计算模型的预测结果,并衡量预测与真实值的误差。
预测输出值的公式: y ^ = w T x + b \hat{y} = w^Tx + b y^=wTx+b
损失函数:衡量预测值与真实值的差异,
均方误差(Mean Squared Error, MSE)公式为:
L ( w , b ) = 1 m ∑ i = 1 m ( y ^ i − y i ) 2 L(w, b) = \frac{1}{m}\sum_{i=1}^{m}(\hat{y}_i - y_i)^2 L(w,b)=m1i=1∑m(y^i−yi)2 其中 y i y_i yi 是第 i i i 个样本的真实值, m m m 是样本数量。
线性回归的目标是最小化损失函数 L ( w , b ) L(w, b) L(w,b),即找到使预测值与真实值平均平方差最小的 w w w 和 b b b。
2.2.2反向传播
反向传播是从 "损失函数" 到 "参数梯度" 的计算过程,核心是通过求导(梯度)找到参数的优化方向,为参数更新提供依据。即根据损失值调整w和b。
梯度:梯度指向函数在该点处增长最快的方向。梯度的模(长度)表示变化率的大小。、、过迭代优化算法
梯度下降法:逐步更新参数,直到损失函数收敛。类比蒙眼爬山时,通过脚底坡度(梯度)感受下山方向,一小步一小步(学习率)往山下走。
w = w − α ⋅ ∂ L o s s ∂ w w = w - \alpha \cdot \frac{\partial Loss}{\partial w} w=w−α⋅∂w∂Loss b = b − α ⋅ ∂ L o s s ∂ b b = b - \alpha \cdot \frac{\partial Loss}{\partial b} b=b−α⋅∂b∂Loss 其中 α \alpha α 是学习率(控制参数更新步长)。学习率太小收敛较慢,太大容易错过最低点(发散)。
2.2.3向量化实现
正向传播:

反向传播:

三、代码实例
数据准备与生成模拟房价数据:
- 这一部分使用 NumPy 随机生成了 100 个样本的房屋数据,包括:面积、房间数、房龄、距离市中心、是否学区房
- 然后根据一个线性组合模型生成房价 house_price,加上高斯噪声,模拟真实情况。
- 得到特征矩阵 X 和目标变量 y,准备后续建模。
python
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# ======================
# 1. 数据准备
# ======================
np.random.seed(42)
n_samples = 100
house_area = np.random.uniform(50, 200, n_samples)
room_num = np.random.randint(1, 7, n_samples)
house_age = np.random.randint(0, 31, n_samples)
distance = np.random.uniform(1, 15, n_samples)
school_district = np.random.randint(0, 2, n_samples)
house_price = (
1.2 * house_area +
15 * room_num -
0.8 * house_age -
3 * distance +
20 * school_district +
np.random.normal(0, 30, n_samples)
)
data = pd.DataFrame({
'面积': house_area,
'房间数': room_num,
'房龄': house_age,
'距离市中心': distance,
'学区房': school_district,
'价格': house_price
})
X = data[['面积', '房间数', '房龄', '距离市中心', '学区房']].values
y = data['价格'].values.reshape(-1, 1)数据标准化 + 分割:
- 对特征矩阵 X 使用 StandardScaler 做标准化,确保不同特征的量纲一致,有利于梯度下降收敛。
- 将数据划分为训练集和测试集(80%训练,20%测试)。得到训练特征 X_train、测试特征 X_test,训练目标 y_train、测试目标 y_test。
python
# ======================
# 2. 数据标准化 + 分割
# ======================
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(
X_scaled, y, test_size=0.2, random_state=42
)
m, n = X_train.shape随机初始化参数:
- 随机生成权重 W(每个特征一个权重)和偏置 b。使用随机值而不是零,避免梯度下降初期对称性问题。
梯度下降训练模型:通过梯度下降学习权重和偏置,让模型拟合训练数据。
- 前向传播:计算预测值 Z = X_train * W + b,并计算损失(MSE)。
- 反向传播:计算损失对参数的梯度
- 参数更新:根据梯度和学习率 lr 更新 W 和 b。
- 循环多轮(epochs=200)迭代,逐步让模型参数收敛。
python
# ======================
# 3. 随机初始化参数
# ======================
np.random.seed(0)
W = np.random.randn(n, 1) # 权重 (n,1)
b = np.random.randn(1) # 偏置 (标量)
# ======================
# 4. 梯度下降
# ======================
lr = 0.05
epochs = 200
for epoch in range(epochs):
# forward
Z = np.dot(X_train, W) + b # (m,1)
loss = np.mean((Z - y_train) ** 2) / 2 # MSE
# backward
dZ = Z - y_train # (m,1)
dW = np.dot(X_train.T, dZ) / m
db = np.sum(dZ) / m
# update
W -= lr * dW
b -= lr * db
if (epoch + 1) % 50 == 0:
print(f"Epoch {epoch + 1}: Loss={loss:.2f}")或者直接调用已有的线性回归模型:
python
# 创建线性回归模型实例
model = LinearRegression()
# 使用训练数据拟合模型,求解w和b
model.fit(X_train, y_train)在测试集上预测:
- 使用训练好的 W 和 b 对测试集 X_test 做预测 y_pred = X_test * W + b。
- 计算测试集均方误差(MSE),评估模型性能。
对新房屋进行预测:
- 创建一个新房屋特征数据 new_house。用训练集的 scaler 对新房屋特征做标准化,保证与训练数据尺度一致。
- 使用训练好的 W 和 b 做线性预测,得到新房屋的预测价格。
python
# ======================
# 5. 在测试集上预测
# ======================
feature_names = ['面积', '房间数', '房龄', '距离市中心', '学区房']
df_test = pd.DataFrame(X_test, columns=feature_names)
df_test['价格'] = y_test
y_pred = np.dot(X_test, W) + b
mse = np.mean((y_pred - y_test) ** 2)
print(df_test.head(10)) # 打印前10行
print("\n最终参数:")
print("W:", W.ravel())
print("b:", b)
print(f"测试集 MSE: {mse:.2f}")
print(f"测试集 RMSE: {np.sqrt(mse):.2f}")
# ======================
# 6. 一组新数据
# ======================
# 创建新房屋特征
new_house = np.array([[120, 3, 5, 8, 1]]) # 120平米, 3室, 5年房龄, 8公里, 学区房
# 标准化(使用训练集的 scaler)
new_house_scaled = scaler.transform(new_house)
# 预测价格
predicted_price = np.dot(new_house_scaled, W) + b
# 打印结果
print("\n新房屋预测结果:")
print(f"房屋特征: 面积{new_house[0,0]}平米, {new_house[0,1]}室, {new_house[0,2]}年房龄, "
f"距离市中心{new_house[0,3]}公里, {'是' if new_house[0,4]==1 else '非'}学区房")
print(f"预测价格: {predicted_price[0,0]:.2f}万元")