三维重建-动手学计算机视觉19（完结）

简介

前面几章介绍了照相机的标定、光流的计算和平行双目视觉，这些都是在探索如何从二维图像中获取三维信息。有了这些知识的铺垫，本章终于要介绍如何从我们日常生活中拍摄的图像中重建三维场景了。首先考虑单幅图像的情况。由于单幅图像无法提供深度信息，因此无法准确估计成像物体的真实尺寸，从而会出现如图19-1所示的视觉错觉。

图19-1单幅图像无法提供深度信息导致的视觉错觉要重建场景几何结构，往往需要多幅图像。第18章介绍了平行双目视觉系统，通过视差，我们能够从平行双目照相机所拍摄的图像对中恢复场景的深度信息。但是在实际生活中，我们所获得的多幅图像往往不是由平行双目照相机拍摄的，在很多情况下，这些图像是由同一台照相机从不同的视角拍摄的。试想，我们在桌面上看到了一个精致的不倒翁，于是手持同一台照相机从不同视角拍摄了两张照片，如图19-2所示。

显然这两幅图像并不符合平行双目视觉系统中两台照相机的光轴平行这一假设，因此不能直接套用平行双目视觉系统中所介绍的方法来计算深度信息。

为了从这些图像中恢复场景的三维信息，我们需要使用照相机模型之间的约束来进行场景的几何结构推理。本章将介绍如何从非平行双目视觉系统拍摄的图像中恢复场景的几何信息，主要内容是对极几何(epipolar geometry)和三角测量(triangulation)。

对极几何

在介绍对极几何之前，先回顾一下平行双目视觉系统。在平行双目视觉系统中，两台照相机水平放置且光轴互相平行。在这种情况下，由于左、右照相机位置只在x轴上有差异，因此空间中一点在左、右照相机成像平面上的像也只在x轴（对应图像的水平轴）上有差异，这就是视差。在非平行双目视觉系统中，两台照相机的光轴不再平行，而是存在一定的会聚度(convergence.),如图19-3所示。

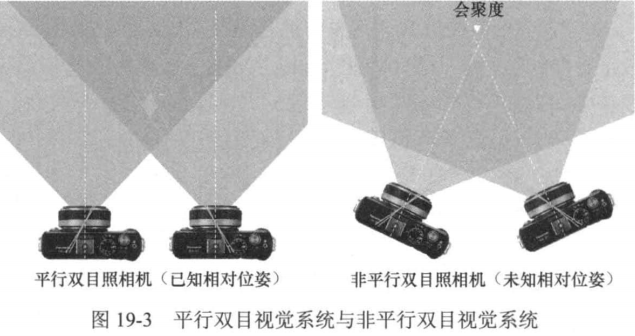
在这种情况下，不能再沿着水平轴寻找左右两个成像平面上的对应点，而必须考虑更复杂的几何关系。我们将在本节中介绍如何通过对极几何来解决这个问题。

对极几何的基本概念

对极几何（Epipolar Geometry）是计算机视觉中用于描述两幅图像之间几何关系的数学框架。它通过极线约束（Epipolar Constraint）简化了立体匹配问题，将搜索空间从二维降至一维。

核心元素

• 极平面（Epipolar Plane）：由两个相机光心和空间点构成的平面。
• 极线（Epipolar Line）：极平面与成像平面的交线。
• 极点（Epipole）：另一个相机光心在当前图像上的投影点。

数学表达

对极几何的核心是对极约束方程：

本质矩阵的分解

本质矩阵可以通过奇异值分解（SVD）分解为：通过分解可以得到相机的旋转矩阵和平移向量

实际操作步骤

1. 特征点匹配：在两幅图像中提取并匹配特征点（如SIFT、ORB等）。
2. 计算基础矩阵 ：使用RANSAC等鲁棒方法从匹配点中估计。
3. 极线校正：通过极线校正（Rectification）将极线对齐为水平线，简化立体匹配。

示例代码（OpenCV）

import cv2
import numpy as np

# 读取图像
img1 = cv2.imread('image1.jpg', 0)
img2 = cv2.imread('image2.jpg', 0)

# 特征点检测与匹配
sift = cv2.SIFT_create()
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)

bf = cv2.BFMatcher()
matches = bf.knnMatch(des1, des2, k=2)

# 筛选匹配点
good = []
for m, n in matches:
    if m.distance < 0.75 * n.distance:
        good.append(m)

pts1 = np.float32([kp1[m.queryIdx].pt for m in good]).reshape(-1, 1, 2)
pts2 = np.float32([kp2[m.trainIdx].pt for m in good]).reshape(-1, 1, 2)

# 计算基础矩阵
F, mask = cv2.findFundamentalMat(pts1, pts2, cv2.FM_RANSAC)

# 绘制极线
def drawlines(img1, img2, lines, pts1, pts2):
    r, c = img1.shape
    img1 = cv2.cvtColor(img1, cv2.COLOR_GRAY2BGR)
    img2 = cv2.cvtColor(img2, cv2.COLOR_GRAY2BGR)
    for r, pt1, pt2 in zip(lines, pts1, pts2):
        color = tuple(np.random.randint(0, 255, 3).tolist())
        x0, y0 = map(int, [0, -r[2]/r[1]])
        x1, y1 = map(int, [c, -(r[2]+r[0]*c)/r[1]])
        img1 = cv2.line(img1, (x0, y0), (x1, y1), color, 1)
        img1 = cv2.circle(img1, tuple(pt1), 5, color, -1)
        img2 = cv2.circle(img2, tuple(pt2), 5, color, -1)
    return img1, img2

# 选取内点
pts1 = pts1[mask.ravel() == 1]
pts2 = pts2[mask.ravel() == 1]

# 计算并绘制极线
lines1 = cv2.computeCorrespondEpilines(pts2.reshape(-1, 1, 2), 2, F)
lines1 = lines1.reshape(-1, 3)
img5, img6 = drawlines(img1, img2, lines1, pts1, pts2)

cv2.imshow('Epilines', np.hstack((img5, img6)))
cv2.waitKey(0)
cv2.destroyAllWindows()

注意事项

• 基础矩阵的估计对噪声敏感，建议使用RANSAC等鲁棒方法。
• 极线校正可以提高立体匹配的效率，但会引入一定的几何失真。
• 对极几何假设场景为静态，动态场景需额外处理。

有关本质矩阵和数学公式推导这里不多加概述

三维重建演示demo:Stable Point-Aware 3D - a Hugging Face Space by stabilityai

代码实现

上面我们已经了解了对极约束的基本概念和推导，以及如何通过对极约束计算基础矩阵和进行三角测量。接下来这一节我们将动手学如何基于两张给定的不同视角图像计算它们之间的基础矩阵并进行三角测量。

# 首先clone对应仓库
!git clone https://github.com/boyu-ai/Hands-on-CV.git

Cloning into 'Hands-on-CV'...
remote: Enumerating objects: 9, done.
remote: Counting objects: 100% (9/9), done.
remote: Compressing objects: 100% (4/4), done.
remote: Total 9 (delta 1), reused 5 (delta 0), pack-reused 0 (from 0)
Receiving objects: 100% (9/9), done.
Resolving deltas: 100% (1/1), done.

import os, cv2, random
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

class FeatureExtractor:
    """
    构建类用于提取SIFT特征。
    """
    def __init__(self, image):
        """
        初始化FeatureExtractor类。
        
        参数:
        - image: (np.ndarray): RGB 形式的图像。
        """
        self.image = image
        # 将图像转换为灰度图
        self.gray = cv2.cvtColor(self.image, cv2.COLOR_BGR2GRAY)
        self.keypoints = None
        self.descriptors = None

    def extract_features(self):
        """
        使用OpenCV的内置函数提取图像中的SIFT特征。
        
        返回:
        - keys: (list): 特征点列表。
        - descriptors: (np.ndarray): 描述子。
        """
        sift = cv2.SIFT_create()
        keys, descriptors = sift.detectAndCompute(self.gray, None)

        # 如果特征点数量小于20个，返回None
        if len(keys) <= 20:
            return None, None
        else:
            self.keypoints = keys
            self.descriptors = descriptors
            return keys, descriptors

def vis_imgs(imgs):
    """
    可视化多张图像。

    参数:
    - imgs: 要可视化的图像列表。
    """
    # 计算图像数量
    num_imgs = len(imgs)
    # 创建画布
    fig = plt.figure(figsize=(10, 10))
    # 遍历每一张图像
    for i in range(num_imgs):
        # 添加子图
        ax = fig.add_subplot(1, num_imgs, i + 1)
        # 显示图像
        ax.imshow(imgs[i])
        # 关闭坐标轴
        ax.axis('off')
    # 显示画布
    plt.show()

为了方便，这里直接提供了照相机的内参（来自照相机本身的数据），当然也可以用在第 16 章中教过的标定获得的内参数据。

def load_instrinsic(path):
    """
    从文件中直接读取内参。
    """
    return np.loadtxt(path).astype(np.float32)

def construct_img_info(img_root):
    """
    从图像中获取特征信息。
    """
    imgs = []
    feats = []
    K = []
    for _, name in enumerate(os.listdir(img_root)):
        if '.jpg' in name or '.JPG' or '.png' in name:
            # 读取图像
            path = os.path.join(img_root, name)
            img = cv2.cvtColor(cv2.imread(path), cv2.COLOR_BGR2RGB)
            imgs.append(img)

            # 提取特征
            feature_ext = FeatureExtractor(img)
            kpt, des = feature_ext.extract_features()

            # 读取内参
            K = load_instrinsic(os.path.join(
                os.path.dirname(img_root), 'K.txt'))
            feats.append({'kpt': kpt, 'des': des})
    return imgs, feats, K

接下来我们计算两张图像间的对应关系，查询并匹配两者之间的特征。

def get_matches(des_query, des_train):
    """
    匹配相关图像特征。

    参数:
    - des_query: (np.ndarray): 查询描述子。
    - des_train: (np.ndarray): 训练描述子。

    返回:
    - goods: (list): 匹配结果。
    """
    # 创建匹配器
    bf = cv2.BFMatcher(cv2.NORM_L2)
    # 获取匹配结果
    matches = bf.knnMatch(des_query, des_train, k=2)
    # 创建goods列表用于存储有用的匹配结果
    goods = []
    # 遍历所有匹配结果
    for m, m_ in matches:
        # 设置阈值为0.65，保留更多的特征
        if m.distance < 0.65 * m_.distance:
            goods.append(m)
    return goods

def get_match_point(p, p_, matches):
    """
    寻找匹配的关键点。

    参数:
    - p: (list[cv2.KeyPoint]): 查询关键点。
    - p_: (list[cv2.KeyPoint]): 训练关键点。
    - matches: (list[cv2.DMatch]): 匹配信息。

    返回:
    - points_query: (np.ndarray): 查询关键点。
    - points_train: (np.ndarray): 训练关键点。
    """
    # 从查询关键点中找到匹配的关键点
    points_query = np.asarray([p[m.queryIdx].pt for m in matches])
    # 从训练关键点中找到匹配的关键点
    points_train = np.asarray([p_[m.trainIdx].pt for m in matches])
    # 返回匹配的查询和训练关键点
    return points_query, points_train

def homoco_pts_2_euco_pts(pts):
    """
    齐次坐标转化为欧几里得坐标。
    """
    if len(pts.shape) == 1:
        pts = pts.reshape(1, -1)
    res = pts / pts[:, -1, None]
    return res[:, :-1].squeeze()

def euco_pts_2_homoco_pts(pts):
    """
    欧几里得坐标转化为齐次坐标。
    """
    if len(pts.shape) == 1:
        pts = pts.reshape(1, -1)
    one = np.ones(pts.shape[0])
    res = np.c_[pts, one]
    return res.squeeze()

def normalize(pts, T=None):
    """
    对点集进行归一化。
    """
    # 如果T参数为空
    if T is None:
        # 求点集的平均值
        u = np.mean(pts, 0)
        # 求点集中每个点与原点之间的距离之和
        d = np.sum(np.sqrt(np.sum(np.power(pts, 2), 1)))
        # 计算归一化矩阵
        T = np.array([
            [np.sqrt(2) / d, 0, -(np.sqrt(2) / d * u[0])],
            [0, np.sqrt(2) / d, -(np.sqrt(2) / d * u[1])],
            [0, 0, 1]
        ])
    # 将点集进行归一化
    return homoco_pts_2_euco_pts(np.matmul(T, 
                euco_pts_2_homoco_pts(pts).T).T), T

到这里我们就已经得到了两张图之间的对应像素关系，接下来使用八点法计算基础矩阵。

def estimate_fundamental(pts1, pts2, num_sample=8):
    """
    计算基础矩阵。

    参数:
    - pts1: (np.ndarray)：匹配特征所得到的训练点集。
    - pts2: (np.ndarray)：匹配特征所得到的查询点集。

    返回:
    - f: (np.ndarray): 基础矩阵。
    """
    n = pts1.shape[0]
    pts_index = range(n)
    sample_index = random.sample(pts_index, num_sample)
    p1 = pts1[sample_index, :]
    p2 = pts2[sample_index, :]
    n = len(sample_index)
    # 归一化点集坐标
    p1_norm, T1 = normalize(p1, None)
    p2_norm, T2 = normalize(p2, None)
    w = np.zeros((n, 9))
    # 构建A矩阵
    for i in range(n):
        w[i, 0] = p1_norm[i, 0] * p2_norm[i, 0]
        w[i, 1] = p1_norm[i, 1] * p2_norm[i, 0]
        w[i, 2] = p2_norm[i, 0]
        w[i, 3] = p1_norm[i, 0] * p2_norm[i, 1]
        w[i, 4] = p1_norm[i, 1] * p2_norm[i, 1]
        w[i, 5] = p2_norm[i, 1]
        w[i, 6] = p1_norm[i, 0]
        w[i, 7] = p1_norm[i, 1]
        w[i, 8] = 1
    # svd分解
    U, sigma, VT = np.linalg.svd(w)
    f = VT[-1, :].reshape(3, 3)
    U, sigma, VT = np.linalg.svd(f)
    sigma[2] = 0
    f = U.dot(np.diag(sigma)).dot(VT)
    # 逆归一化
    f = T2.T.dot(f).dot(T1)

    ### 随机计算的F矩阵误差较大，使用OpenCV中的函数(RANSAC)计算F矩阵
    pts1 = pts1.astype(np.float32)
    pts2 = pts2.astype(np.float32)
    f, mask = cv2.findFundamentalMat(pts1, pts2, cv2.FM_RANSAC)

    return f

def convert_F_to_E(F_single, K):
    """
    根据F矩阵计算E矩阵。
    """
    inverse_K = np.linalg.inv(K)
    E_single = inverse_K.T.dot(F_single).dot(inverse_K)
    return E_single

def get_Rt_from_E(E_single,K,pts1,pts2):
    """
    根据E矩阵计算Rt，使用OpenCV的函数recoverPose。
    """
    # OpenCV的recoverPose函数已经自动去除了不合理的3个解
    _, R, t, _ = cv2.recoverPose(E_single, pts1, pts2, K) 
    return R, t

def build_F_E_matrix(feats, K):
    """
    计算基础矩阵F，本质矩阵E，从E中分离出Rt并返回。
    """
    pair = dict()
    match = dict()
    Rts = dict()

    for i in range(len(feats)):
        for j in range(i + 1, len(feats)):
            matches = get_matches(
                feats[i]['des'], feats[j]['des'])
            pts1, pts2 = get_match_point(
                feats[i]['kpt'], feats[j]['kpt'], matches)
            assert pts1.shape == pts2.shape
            
            # 至少需要8个点来计算F矩阵
            if pts1.shape[0] < 8:
                continue
            # 计算F矩阵
            F_single = estimate_fundamental(pts1, pts2)
            # 根据F矩阵计算E矩阵
            E_single = convert_F_to_E(F_single, K)
            # 从E矩阵中得到相对位姿
            R, t = get_Rt_from_E(E_single, K, pts1, pts2)

            if pts1.shape[0] < 8:
                continue

            pair.update({(i, j): {'pts1': pts1, 'pts2': pts2}})
            match.update({(i, j): {'match': matches}})
            Rts.update({(i, j): {'R': R, 't': t}})

    return F_single, E_single, pair, match, Rts

img_root = 'Hands-on-CV/第19章 三维重建/images'
imgs, feats, K = construct_img_info(img_root)
# 可视化图像
vis_imgs(imgs)

F, E, pair, match, Rts = build_F_E_matrix(feats, K)
print("基础矩阵为:\n", F)
print("本质矩阵为:\n", E)

# 不妨假定第一张图为世界坐标系
R_t_0 = np.array([[1,0,0,0], [0,1,0,0], [0,0,1,0]])
R_t_1 = np.empty((3,4))
R_t_1[:,:3] = Rts[(0,1)]['R']
R_t_1[:,3] = Rts[(0,1)]['t'].reshape(3)
P_0 = K.dot(R_t_0)
P_1 = K.dot(R_t_1)
print("第一副图像对应的矩阵为:\n", P_0)
print("第二幅图像对应的矩阵为:\n", P_1)

基础矩阵为:
 [[ 5.17116489e-06 -9.35405231e-06 -1.13783351e-03]
 [ 5.94850943e-06  1.16772622e-05 -5.72937517e-03]
 [-2.94980264e-03  3.55455633e-03  1.00000000e+00]]
本质矩阵为:
 [[ 1.80790150e-11 -3.27683889e-11 -2.12631708e-06]
 [ 2.08383558e-11  4.09888034e-11 -1.07495911e-05]
 [-5.52573986e-06  6.66134548e-06  1.00331656e+00]]
第一副图像对应的矩阵为:
 [[534.81896973   0.         320.           0.        ]
 [  0.         533.75       213.           0.        ]
 [  0.           0.           1.           0.        ]]
第二幅图像对应的矩阵为:
 [[ 6.02699217e+02 -1.32348682e+02 -8.75717417e+01  5.27600711e+02]
 [ 1.51538241e+02 -1.73321278e+02  5.26549104e+02  8.74049809e+01]
 [ 3.23134701e-01 -9.46352981e-01  1.82851868e-05  3.84515925e-06]]

在得到了基础矩阵之后，我们就可以通过三角测量计算出三维空间点的坐标。

def filter_matches_by_epipolar(pts1, pts2, F, threshold=3.0):
    """
    使用对极约束过滤匹配点
    
    参数:
    - pts1, pts2: 匹配点对。
    - F: 基础矩阵。
    - threshold: 对极误差阈值。
        
    返回:
    - pts1_filtered, pts2_filtered: 过滤后的匹配点。
    """
    pts1_reshaped = pts1.T.reshape(-1,1,2)
    pts2_reshaped = pts2.T.reshape(-1,1,2)
    
    # 计算两幅图像的极线
    lines1 = cv2.computeCorrespondEpilines(pts2_reshaped, 2, F)
    lines2 = cv2.computeCorrespondEpilines(pts1_reshaped, 1, F)
    
    dist1 = np.abs(np.sum(lines1.reshape(-1,3) * 
                 np.hstack((pts1.T, np.ones((pts1.shape[1],1)))), axis=1))
    dist2 = np.abs(np.sum(lines2.reshape(-1,3) * 
                 np.hstack((pts2.T, np.ones((pts2.shape[1],1)))), axis=1))
    
    mask = (dist1 < threshold) & (dist2 < threshold)
    return pts1[:,mask], pts2[:,mask]

pts1 = np.transpose(pair[(0,1)]['pts1'])
pts2 = np.transpose(pair[(0,1)]['pts2'])
# 过滤匹配点
pts1_filtered, pts2_filtered = filter_matches_by_epipolar(pts1, pts2, F)
print("过滤前的匹配点数量为: ", pts1.shape[1])
print("过滤后的匹配点数量为: ", pts1_filtered.shape[1])

# 三角测量获得空间点坐标
points_3d = cv2.triangulatePoints(P_0, P_1, pts1_filtered, pts2_filtered)
# 齐次坐标的最后一行为1，需要除以最后一行
points_3d /= points_3d[3]
points_3d = points_3d[:3, :].T
print("得到的三维点为:\n", points_3d)

# 计算有效点占像素比例
print("检测到的点占图像像素的比例为: {:02f}%".format(
    points_3d.shape[0]/len(imgs[0][...,0].flatten())*100))

过滤前的匹配点数量为:  16
过滤后的匹配点数量为:  13
得到的三维点为:
 [[-0.60458395 -0.01198244  0.0969504 ]
 [-0.58099777 -0.21461379  0.05341815]
 [-0.47523613 -0.39286399 -0.15945556]
 [-0.56740703 -0.24286074 -0.00477856]
 [-0.49754951 -0.36653935 -0.14429421]
 [-0.47079379 -0.40467599 -0.19146369]
 [-0.55889738 -0.26988774 -0.09548055]
 [-0.60761656 -0.14041958 -0.12032324]
 [-0.56458993 -0.29775277 -0.2171921 ]
 [-0.6082215  -0.14859759 -0.13404173]
 [-0.43299244 -0.4819224  -0.33418579]
 [-0.5657818  -0.3328847  -0.29034157]
 [-0.5657818  -0.3328847  -0.29034157]]
检测到的点占图像像素的比例为: 0.004757%

可以发现，存在部分匹配点不严格遵循对极约束。接下来我们可视化极线和匹配点。

def draw_epipolar_lines(pts1, pts2, img1, img2, F):
    """
    绘制极线。

    参数:
    - pts1: (np.ndarray): 第一幅图像中的匹配点。
    - pts2: (np.ndarray): 第二幅图像中的匹配点。
    - img1: (np.ndarray): 第一幅图像。
    - img2: (np.ndarray): 第二幅图像。
    - F: (np.ndarray): 基础矩阵。
    """
    # 将点坐标转为整数
    pts1 = np.int32(pts1)
    pts2 = np.int32(pts2)

    # 选取前8个点进行可视化
    idx = np.arange(8)
    pts1 = pts1[idx]
    pts2 = pts2[idx]

    # 计算对应的极线
    lines1 = cv2.computeCorrespondEpilines(
                        pts2.reshape(-1,1,2), 2, F)
    lines1 = lines1.reshape(-1,3)

    # 绘制极线
    imgl, imgr = drawlines(img1, img2, lines1, pts1, pts2)

    # 将两幅图拼接在一起
    vis = np.concatenate((imgl, imgr), axis=1)

    # 展示图像
    plt.figure(figsize=(10, 10))
    plt.imshow(vis)
    plt.axis('off')
    plt.show()

def drawlines(img1, img2, lines, pts1, pts2):
    """
    绘制极线。

    参数:
    - img1: (np.ndarray): 左图。
    - img2: (np.ndarray): 右图。
    - lines: (np.ndarray): 极线。
    - pts1: (np.ndarray): 左图对应的匹配点。
    - pts2: (np.ndarray): 右图对应的匹配点。
    """
    # 获取图像尺寸
    r, c, _ = img1.shape

    for r, pt1, pt2 in zip(lines, pts1, pts2):
        color = tuple(np.random.randint(50, 255, 3).tolist())
        # 计算直线上的两个点
        x0, y0 = map(int, [0, -r[2]/r[1]]) 
        x1, y1 = map(int, [c, -(r[2]+r[0]*c)/r[1]])
        # 在img1中绘制直线
        img1 = cv2.line(img1,  (x0, y0),  (x1, y1),  color, 1) 
        # 在img1中绘制对应的特征点
        img1 = cv2.circle(img1, tuple(pt1), 5, color, -1) 
        # 在img2中绘制对应的特征点
        img2 = cv2.circle(img2, tuple(pt2), 5, color, -1) 
    return img1, img2

# 在原图上可视化特征点对应的极线
draw_epipolar_lines(pts1_filtered.T, pts2_filtered.T, 
                    imgs[0], imgs[1], F)

小结

本章探讨了三维重建的基础知识，重点关注了对极几何和三角测量的原理。我们通过对极约束求解基础矩阵并进一步分解以求得照相机的位姿，随后利用三角测量确定空间中点的三维坐标。尽管只得到了非常稀疏的三维点坐标，但这些点的坐标是高度可靠的，为场景提供了必要的三维结构支撑，为后续的深入分析和应用打下了坚实的基础。从二维图像中恢复出三维结构无疑是一项具有挑战性的任务。本章介绍的内容虽然只涵盖了一些基本的三维重建方法，但这些方法为理解和构建更复杂的三维视觉系统奠定了重要的基础。希望读者能从这些初步的概念中领悟三维重建的核心思想，并在此基础上进一步探索和扩展。

计算机视觉技术在大数据时代的发展展望

计算机视觉领域正经历着由大数据和大模型驱动的变革，以下从三个关键方向分析其发展趋势。

视觉大模型的兴起

深度自注意力神经网络（如Transformer）正逐步取代传统卷积神经网络（CNN）成为视觉任务的主流架构。自注意力机制的优势包括：

• 更强的长程依赖建模能力，适用于复杂图像结构
• 隐式参数共享提升模型泛化性能
• 对大尺度数据具备更优的拟合能力 典型案例如ViT（Vision Transformer）系列模型，在ImageNet等基准任务上超越传统CNN模型。

无监督预训练范式的普及

掩模图像建模（Masked Image Modeling, MIM）成为视觉预训练的新范式：

• 通过随机遮蔽图像块并重建原始像素的自监督学习
• 消除对人工标注数据的依赖，可利用海量未标注数据
• 预训练模型经微调后可快速适配下游任务 该方法已在BEiT、MAE等模型中验证有效性，显著降低特定任务的标注成本。

多模态融合的突破

跨模态学习推动视觉与其他领域的协同发展：

• 视觉-语言预训练模型（如CLIP）实现跨模态特征对齐
• 统一架构处理图像、文本、语音等多模态输入
• 零样本迁移能力拓展模型应用边界 技术挑战包括模态对齐、异构数据融合及计算效率优化。

总之，大数据、大模型时代将为计算机视觉技术带来许多机遇和挑战。透过大规模数据和强大的计算能力，我们可以期待计算机视觉技术在自动驾驶、人机交互、视频监控、医学影像辅助诊断等场景下的更多落地应用。

参考链接：动手学计算机视觉 - 动手学计算机视觉